一种改进的上行信道估计算法
2014-07-18王华华
王华华, 吕 南, 张 莉
(重庆邮电大学 通信与信息工程学院, 重庆 400065)
一种改进的上行信道估计算法
王华华, 吕 南, 张 莉
(重庆邮电大学 通信与信息工程学院, 重庆 400065)
为了提高长期演进(Long Term Evolution, LTE)系统上行信道估计的准确性,同时适当的降低信道估计算法的复杂度,针对上行物理共享信道(Physical Uplink Shared Channel, PUSCH),对基于离散傅里叶变换(Discrete Fourier Transform, DFT)的内插滤波信道估计算法进行改进,采用递归最小二乘法(Recursive Least-Squares,RLS)代替原有的内插滤波。根据Matlab仿真结果,提出的新算法在提高信道估计准确度和降低算法复杂度上可以得到有效的均衡。
上行信道;信道估计;离散傅立叶变换;递归最小二乘法
长期演进(Long Term Evolution, LTE)系统作为准4G技术,以正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)和多输入多输出(Multiple-Input Multiple-Output,MIMO)技术为基础[1]。在LTE系统中,保持子载波的正交性、MIMO系统的空时解码、多个天线端口的信号的识别以及系统的同步都需要准确的信道状态信息,系统的整体性能将受到信道状态信息的直接影响。如果不能有效的估计出当前移动通信无线信道的状态信息,那么接收端将不可能准确无误的恢复出发射端发送的数据信息,因此,信道估计是LTE系统中一个非常重要的环节。
上行信道估计一般采用的是基于导频符号的信道估计算法,主要包括基于导频的信道响应的估计和完整信道响应的估计。导频位置的信道估计的准则有最小平方(Least Square, LS)、线性最小均方误差(Linear least mean-square error,LMMSE)等,完整信道响应的估计传统上有线性插值[2]、基于离散傅里叶变换(Discrete Fourier Transform, DFT)的时域插值、基于DFT的内插滤波信道估计算法等[3]。这些算法虽然计算简单且容易实现,但信道估计的准确度有待于进一步的提高。
本文在目前算法的基础上用递归最小二乘法(Recursive Least-Squares,RLS)代替内插滤波,提出了基于DFT的RLS信道估计算法。
1 长期演时上行信道描述
1.1 上行物理共享信道
以上行物理共享信道(Physical Uplink Shared Channel, PUSCH)为例,图1给出了PUSCH信道的系统模型[4-5]。上行共享信道首先对从上层接收到数据进行循环冗余校验(Cyclic Redundancy Check, CRC)添加、信道编码、速率匹配等,然后进入基带处理部分[2],即调制、加扰、传输预编码、资源映射以及单载波频分多址Single-carrier Frequency-Division Multiple Access, SC-FDMA)调制,最后经天线发送出去。而在接收端,天线则对接收的数据进行SC-FDMA解调、解资源映射、信道估计、信道均衡、解传输预编码、解调、解扰、解速率匹配、信道译码以及CRC校验。

图1 上行物理共享信道系统模型
1.2 上行解调参考信号
LTE上行发送的每个SC-FDMA符号都要在前面添加循环前缀(Cyclic Prefix, CP)以便消除符号间干扰,PUSCH解调参考信号(Demodulation Reference Signal, DMRS)映射的频域位置与CP的类型有关。普通CP情况下,解调参考信号映射在每个子帧的第3个和第10个SC-FDMA符号上;扩展CP情况下,解调参考信号映射在每个子帧的第2个和第9个SC-FDMA符号上[6]。
PUSCH信道在时域上周期性的插入解调参考信号,且解调参考信号会占满整个位于该时域符号上的所有频域资源。所以,PUSCH信道的信道估计只需要时域插值即可。PUSCH信道普通循环前缀的解调参考信号映射结构如图2所示[5]。

图2 PUSCH信道DMRS的结构
在图2中,每个时隙包含7个SC-FDMA符号,阴影部分表示导频信息,其余表示数据信息。
1.3 导频子载波的信道估计算法
1.3.1 LS估计法
假设Yp、Xp和Hp分别代表导频位置上的接收信号、信道响应的估计值和发送导频值。基于最小平方准则,定义代价函数为
(1)
(2)
其中Wp是在导频位置上的噪声干扰。由式(2)可以看出,基于LS准则的导频信道估计算法结构简单,计算量小,复杂度低,实现起来非常简单,但当信道噪声较大时,LS的准确性会明显降低,所以一般会用基于LMMSE的导频信道估计来代替它。
1.3.2 LMMSE估计法

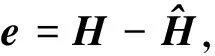
则其均方误差(Mean Square Error, MSE)为

(3)
LMMSE算法就是使得E[|e|2]最小,因此可得LMMSE算法的信道估计为[7-8]
(4)
其中σ2为噪声方差。
由式(4)可以知道,LMMSE算法充分利用了自相关矩阵RHH,提高了信道估计的精确度,同时降低了MMSE算法的复杂度。
2 上行信道估计算法及改进
2.1 基于线性插值的算法
由于PUSCH信道中一个子帧中只在特定符号上包含2个参考信号,所以可以采用线性插值的方法获取整个子帧的信道响应值。如果在子帧中两个参考信号符号分别为l1和l2,则可以采用以下的插值方式。
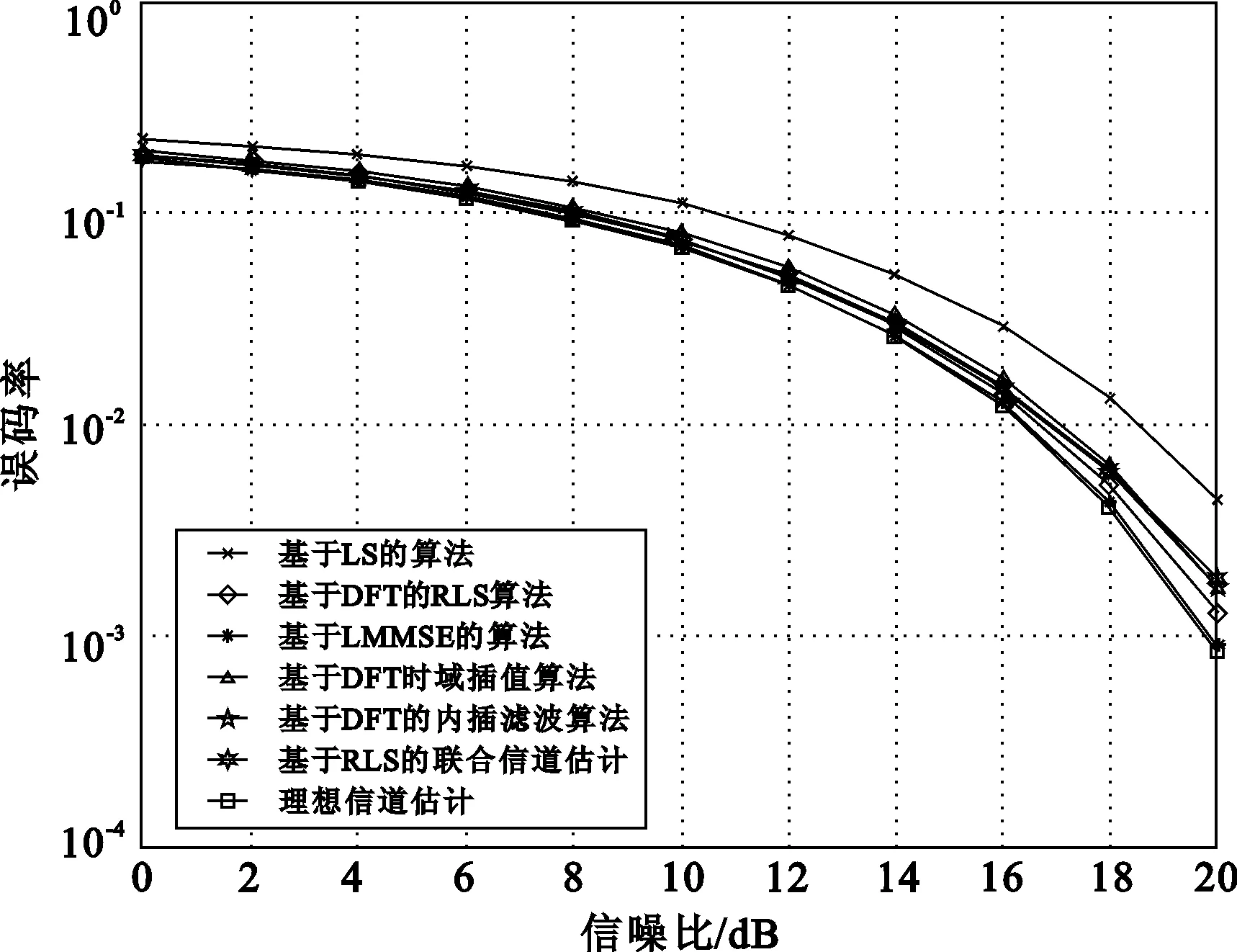
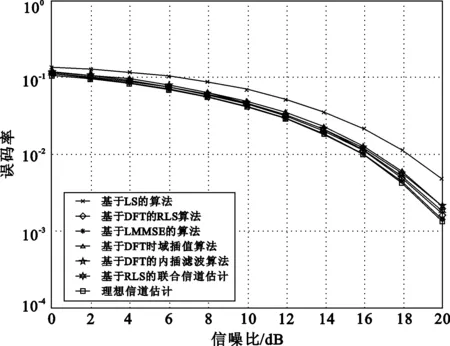
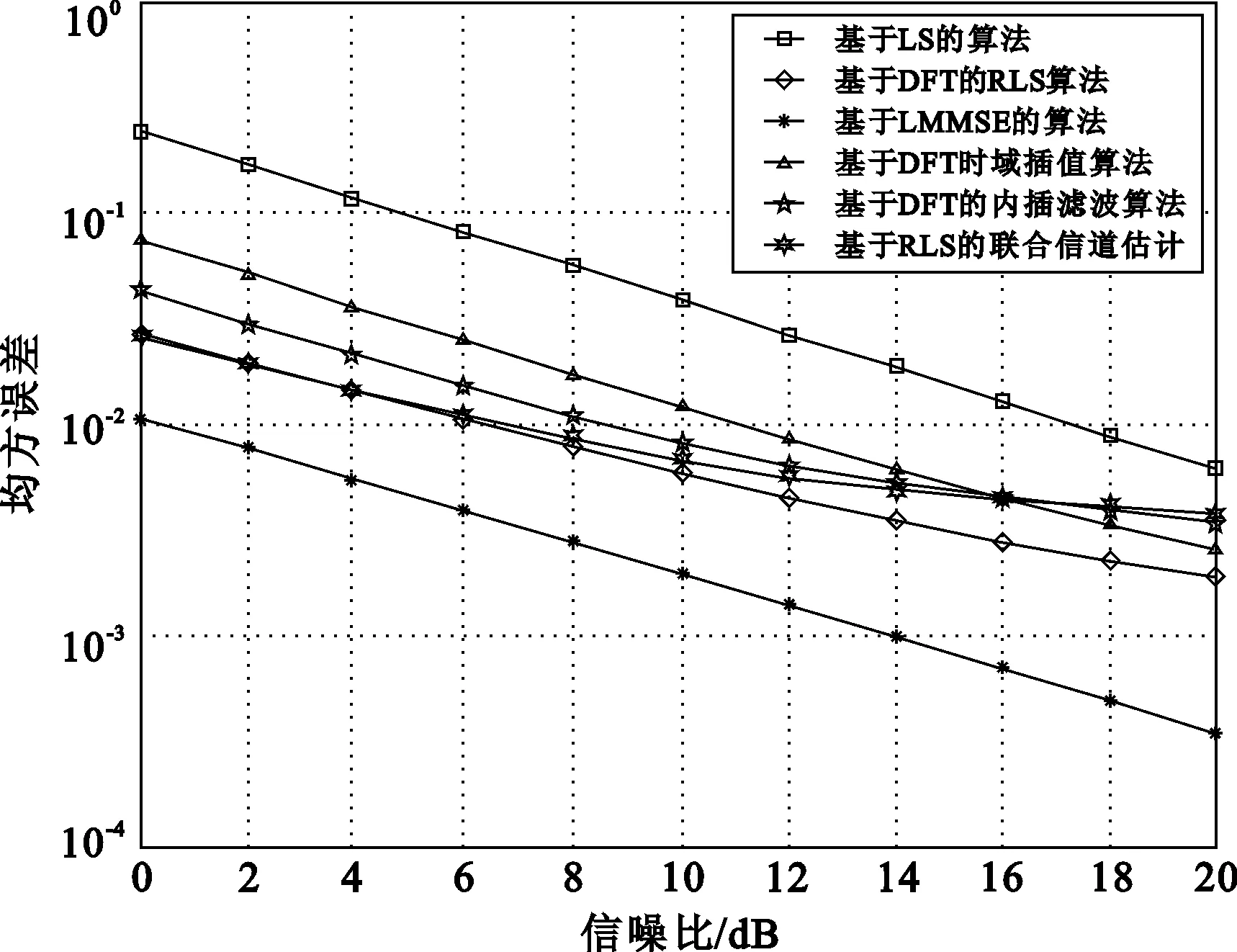
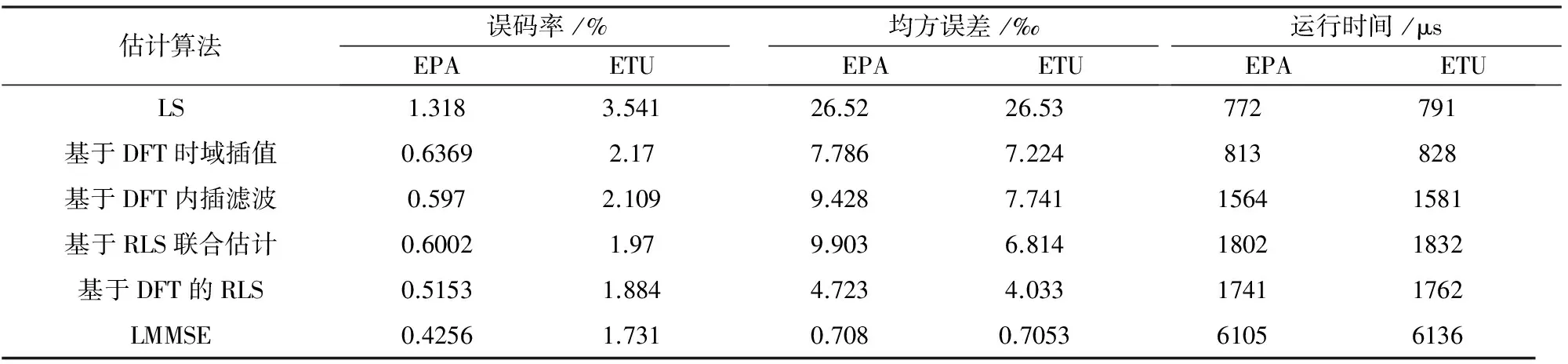
对于l H(k,l)=H(k,l1)。 (5) 对于l1 (6) 对于l>l2,即位于参考信号符号l2之后的数据符号的信道响应为 H(k,l)=H(k,l2)。 (7) 线性插值算法复杂度不高,实现简单,是信道估计中常用的方法之一,但信道估计的准确度不是非常精确。 2.2 基于DFT的内插滤波算法 基于DFT的内插滤波算法的流程如图3所示,其中Hp为导频位置信道估计值,则该算法的具体步骤如下[3,9]。 步骤3 对时域冲激响应h进行加窗和门限滤波处理,其中加窗算法为 (8) 门限滤波算法为 (9) 图3 基于DFT的内插滤波算法流程 2.3 基于DFT的RLS估计算法 基于DFT的RLS算法与基于DFT的内插滤波算法唯一的不同之处在于用RLS算法取代了门限滤波这一步骤。 步骤1(算法初始化) 设 其中δ在高信噪比时取小的正数,而在低信噪比时取大的正数。 步骤2(迭代过程) 对每个时刻n(n=1,2,…) 依次计算 π(n)=P(n-1)u(n), (10) (11) (12) (13) P(n)=λ-1P(n-1)-λ-1k(n)uH(n)P(n-1)。 (14) 3.1 仿真条件及参数 在仿真实验中,运用蒙特卡洛方法对传统和优化算法进行仿真分析。选取多普勒频移为5 Hz的扩展步行模式A(Extended Pace A, EPA)信道和多普勒频移为300 Hz的扩展典型城市模式(Extended Typical Urban, ETU)信道作为仿真信道,信道参数和仿真参数分别如表1和表2所示。 表1 信道参数 表2 仿真参数 3.2 结果及分析 图4所示为在EPA(5 Hz)和ETU(300 Hz)两种信道条件下的基于LS的估计算法、基于LMMSE的估计算法、基于DFT的时域插值算法、基于DFT的内插滤波算法、基于DFT的RLS算法、基于RLS的联合估计以及理想估计这七种算法的误码率(Block Error Rate, BER)性能仿真比较图。其中理想信道估计指的是信道条件比较理想,没有噪声及多普勒频移等因素的影响。 (a) 扩展步行模式 A (b) 扩展典型城市模式 如图4所示,在BER为10-2时,基于DFT的RLS算法和基于RLS的联合信道估计算法比基于LS的信道估计算法低2 dB。当信噪比低于2 dB时,各种信道估计算法的性能趋向一致,随着信噪比的增加,基于DFT的RLS算法和基于RLS的联合信道估计算法的性能逐渐增强。 由图4可以看出,EPA信道条件下的BER要比ETU信道条件下的低,这是因为EPA信道环境没有ETU信道环境复杂。 在EPA(5 Hz)和ETU(300 Hz)这两种信道条件下,LS信道估计算法、LMMSE信道估计算法、基于DFT的时域插值算法、基于DFT的内插滤波算法、基于DFT的RLS算法以及基于RLS的联合信道估计算法的均方误差(MSE)性能仿真比较如图5所示。 (a) 扩展步行模式 A (b) 扩展典型城市模式 由图5可见,当信噪比小于10 dB时,基于DFT的RLS算法和基于RLS的联合估计算法的MSE小于LS算法、基于DFT的时域插值算法以及基于DFT的内插滤波算法,而当SNR大于10 dB时,基于DFT的RLS算法和基于RLS的联合估计算法的性能都会变差,但是后者变差的速度更快甚至可能低于基于DFT的时域插值的算法性能。 为了清晰表达基于DFT的RLS信道估计算法在性能及时间复杂度上的均衡,文中进行了10 000次Matlab仿真从而对比各种算法的运行时间,当SNR为18 dB时,各种算法的MSE和BER如表3中所示。 表3列出了各种算法的性能比较以及运行时间。若以EPA(5 Hz)为例,可以得出以下结论。 (1) 基于DFT的RLS算法与基于DFT的内插滤波算法相比,运行时间增加了10%,同时BER和MSE分别降低了14%和50%。 (2) 与基于LMMSE的信道估计算法相比,基于DFT的RLS算法虽然MSE和BER有所增加,但是运行时间缩小了71%。所以基于DFT的RLS信道估计算法的设计正确性、性能及时间复杂度上有效的均衡性得到证明。 表3 BER和MSE与运行时间的对比 对比了基于DFT的RLS信道估计算法、基于RLS的联合信道估计算法与LS算法、基于DFT的时域插值算法、基于DFT的内插滤波算法、LMMSE算法在LTE下行信道估计中的性能,分别对各种算法的MSE、BER和时间复杂度进行仿真,得出基于DFT的RLS信道估计算法能够在性能和时间复杂度上进行很好的均衡。 [1] 王映民,孙韶辉.TD-LTE 技术原理与系统设计[M].北京:人民邮电出版社,2010:15-19. [2] 郭强,谢丽丽,钱治军.LTE上行信道估计算法研究[J].电子元器件应用,2010,12(6):75-78. [3] 文汝红.基于DFT的信道估计插值算法改进[J].宜春学院学报,2012,34(4):10-12. [4] 3GPP TS 36.212 v9.1.0. Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and channel coding (Release 9)[EB/OL].(2010-06-30)[2013-11-01].http://www.3gpp.org, Mar. 2010. [5] 沈嘉,索士强,全海洋,等.3GPP长期演进(LTE)技术原理与系统设计[M].北京:人民邮电出版社,2008:45-49. [6] 3GPP TS 36.211 v9.1.0. Evolved Universal Terrestrial Radio Access (E-UTRA); Physical Channels and Modulation (Release 9)[EB/OL].(2010-10-09)[2013-11-01].http://www.3gpp.org, Mar. 2010. [7] 张欣,彭端,张子杰,等.基于LTE上行的改进LMMSE信道估计算法[J].计算机技术与发展,2012,22(6):97-99. [8] 战金龙,方会妮,郑亮.长期演进系统上下行信号识别算法[J].西安邮电学院学报,2012,17(2):9-12. [9] 何婷.基于LTE的信道估计技术研究[D].武汉:武汉理工大学,2010:23-26. [10] 李殿为.LTE系统上行链路信道估计算法研究[D].哈尔滨:哈尔滨工业大学,2011:53-56. [责任编辑:王辉] An improved algorithm for uplink channel estimation WANG Huahua, LYU Nan, ZHANG Li (School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China) In order to improve the accuracy of uplink channel estimation and reduce the algorithm complex of it, an improved channel estimation algorithm based on the Interpolation filtering algorithm using the Discrete Fourier Transform (DFT) for the Physical uplink shared channel(PUSCH) is proposed in this paper. The new method uses Recursive Least-Squares (RLS) to replace the method based on traditional interpolation filtering. The matlab simulation results show that the new algorithm can effectively balance improving accuracy and reducing complexity of channel estimation algorithm. uplink channel, channel estimation, discrete Fourier transform, recursive least-squares 10.13682/j.issn.2095-6533.2014.01.004 2013-11-27 国家科技重大专项基金资助项目(2011ZX03001-002) 王华华(1981-),男,硕士,高级工程师,从事第四代移动通信技术研究与开发。E-mail:zhangliv0830@126.com 吕南(1987-),男,硕士研究生,研究方向为通信与信息系统。E-mail:zhanglilv0830@126.com TN929.5 A 2095-6533(2014)01-0021-05




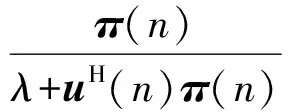
3 仿真结果及分析



4 结束语
