基于RWG矩量法的短波天线辐射性能分析

陈 斌， 赵 鹏， 杨路刚， 颜 慧

(1.海军工程大学 电子工程学院， 湖北 武汉 430033； 2.解放军91917部队， 北京 102100)

基于RWG矩量法的短波天线辐射性能分析

陈 斌1， 赵 鹏1， 杨路刚1， 颜 慧2

(1.海军工程大学 电子工程学院， 湖北 武汉 430033； 2.解放军91917部队， 北京 102100)

RWG矩量法在短波天线和地面全剖分时数据量过大且地面效应不足，针对由此引起的计算准确度偏低问题，提出一种新的计算模型。新模型引入辅助三角形对短波接地天线馈源模型进行改进，以理想导电半空间场型并矢格林函数作为电场积分方程的积分内核，RWG边元仅剖分天线辐射体。采用矩量法离散电场积分方程，分析阻抗矩阵计算中的奇异积分和高震荡性问题，引入9点积分法予以解决。以短波鞭状天线为例，进行场强方向图和输入阻抗的仿真，结果与商用电磁仿真软件FEKO以及公开的文献吻合较好。新模型可减小计算量和仿真时间，提高计算准确度。

矩量法；阻抗矩阵；并矢格林函数；短波天线；辐射性能

天线的辐射性能直接影响无线电通信系统的整体性能。天线辐射性能分析本质上是满足一定边界条件的电磁场数值计算问题。矩量法[1]主要用于求解电磁场积分方程，利用基函数近似展开未知函数，代入算子方程，在权函数的加权平均下使方程的余量为零。矩量法的研究主要围绕基函数和权函数的选取方法、如何处理奇异点、积分方程和离散矩阵之间的关系以及矩阵方程的快算求解算法四个方面展开。

文献[2]利用三角形边元(Triangular Edge Element)共形任意形状散射体曲面，提出RWG(RAO-Wilton-Glisson)矢量基函数，系统地论述了RWG矩量法中子域基函数的建立和电场积分方程的解析；文献[3]论述了数值积分的二维和三维解，为连续积分的数值计算提供途径；文献[4]将边馈电模型引入天线网格结构，用δ函数表示馈电缝隙中的电场，在分析地面上天线时存在数据量过大且地面效应不足的问题；文献[5]在RWG矩量法分析金属球表面天线时引入极限的思想设置共形面结合处的馈源;文献[6-7]利用指数谱函数研究了地面电磁散射特性的参数反演问题。

本文基于以上研究成果，重点分析文献[4]给出的地面上天线模型的不足，引入辅助三角形和理想导电半空间并矢格林函数，提出一种新的计算模型。针对阻抗矩阵计算中的奇异积分和高震荡性问题，采用9点积分法进行计算。以短波鞭状天线为例，进行场强方向图和输入阻抗的计算，与FEKO仿真结果进行对比，以验证算法的正确性和有效性。

1 积分方程和RWG矩量法

1.1 电场积分方程

实际短波鞭状天线架设时会铺设地网，地面可用无限大理想导电平面来近似处理，与其上层空气构成理想导电半空间。由镜像原理可知，理想导电半空间并矢格林函数是原电流源并矢格林函数及其镜像的叠加[8]

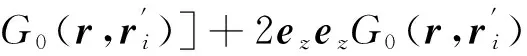
(1)

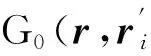
根据导体表面边界条件可得到理想导电半空间中电场积分方程

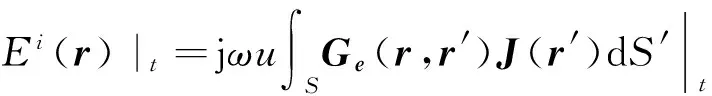
(2)

其中Ei(r)表示馈源激发的电场，Ge(r,r′)是理想导电半空间并矢格林函数，J(r′)表示天线表面电流分布，jωu∫SGe(r,r′)J(r′)dS′是天线辐射电场的并矢格林函数积分解，u和ω分别表示磁导率和工作角频率，|t表示切向分量。

对Ge(r,r′)作本征展开，文献[8]中引入L,M和N三类矢量波函数，采用欧姆-瑞利方法求解，限于篇幅，这里不再进行推导。

1.2 RWG矩量法

基函数和权函数用于拟合未知函数，拟合误差越小，计算精度越高，收敛越快。RWG矩量法将散射体表面具有公共边的一对三角形定义为RWG边元，定义边元域上矢量基函数[2]

(3)

其中T±是RWG边元的一对三角形，其中心为rc±，l是其公共边长度，r是两三角形中任一点，ρ+(r)是由T+的自由顶点指向r的矢量，ρ-(r)是由r指向T-的自由顶点的矢量。

以RWG矢量基函数展开表面电流分布J,可得

(4)

其中N是RWG边元的个数，In是扩展系数。将式(1)和式(4)代入式(2)，采用伽辽金法[9]，可得

∫ΔmEi(r)fm(r)dS=

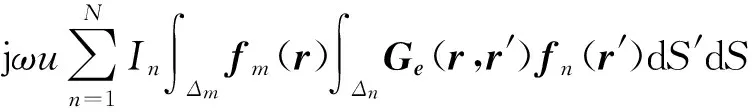
(5)

其中Δ表示边元三角形面。将式(5)写成矩阵形式，可得系统矩量方程

[zmn][In]=[vm],

(6)

其中

zmn=jωu∫Δmfm(r)∫ΔnGe(r,r′)fn(r′)dS′dS,

(7)

vm=∫ΔmEi(r)fm(r)dS。

(8)

解矩量方程可得扩展系数矢量[In]。 RWG矩量法将边元的电流分布等效为无穷小偶极子，所有无穷小偶极子辐射场的叠加可得到总辐射场。偶极子矩量由表面电流在三角形面上积分解得

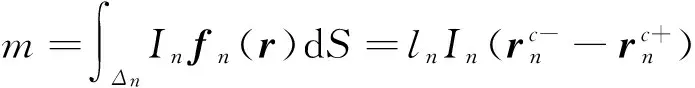
(9)

无穷小偶极子辐射场的计算可由文献[10]得到，这里不再给出。

2 模型的改进

对于馈电源，用一个RWG边元的公共边做驱动边，模拟馈电缝隙内的电场[11]，缝隙两端跨接馈电电压V，当缝隙间距趋于无穷小时，其电场可用δ函数表示，即所谓δ函数函数发生器法[4]，该边元作为馈电边元，其激励电压为V，矩量可计算为

m=∫Δnδ(z)ezf(r)dS=1nV。

(10)

文献[4]中以RWG边元剖分整个天线辐射体和地面，利用自由空间标量格林函数和位函数方程计算天线辐射场，该模型存在两个方面的缺陷：由于地面尺寸有限，地面效应不足，模型对鞭状天线的仿真是不准确的；当地面尺寸增加时，RWG边元数目迅速增大，运算量急剧上升，对计算机的处理速度提出更高要求。以10 m单鞭天线为例，在频率为27 MHz情况下，取边元尺寸为λ/10(λ表示波长)，边元数目随地面(以平面正方形表示)尺寸变化的曲线如图1所示。

图1 地面尺寸与边元数量关系

图1表明，地面尺寸增加时边元数量迅速增加，地面尺寸为5λm × 5λm时，边元数量达到8 965个，阻抗矩阵是8 965阶方阵，边元利用率即天线辐射体边元数与地面边元数之比仅3.6×10-3，当地面尺寸增加到10λm × 10λm时，边元数量大于1.5×104，对应阶数超过2.25×108阶的方阵，计算量过大，此时边元利用率几乎为0。对于鞭天线网格结构，仅仅采用镜像法处理会使馈电边元和辐射体其他边元阻抗关系发生变化。针对以上问题，引进辅助三角形来改进馈源模型，只剖分天线辐射体，通过理想导电半空间并矢格林函数计算天线辐射场。在馈电缝隙处增加一对水平方向的辅助三角形，以构造驱动边元，如图2所示。

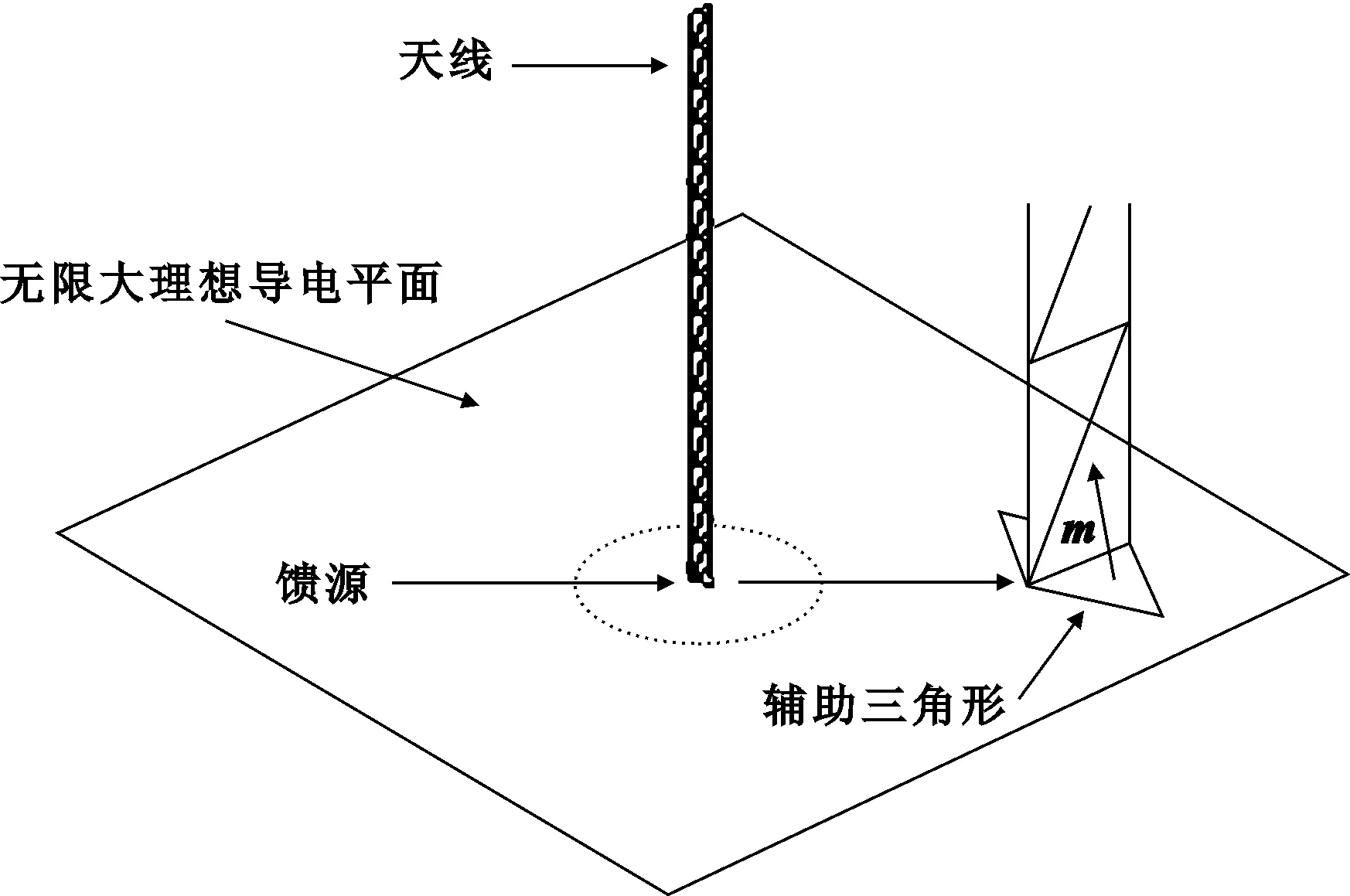
图2 天线结构

该模型(以下称改进模型)使用带状结构[12]等效理想导线构成天线辐射体，其底部与平面的交线使2个辅助三角形和对应的带上三角形构成RWG边元，该边元作为馈电边元，保证馈电边元和辐射体边元阻抗关系不变。整个网格结构边元数下降到32个，比原模型下降近99%(地面尺寸不小于3λm × 3λm)，但仿真性能有较大提高，采用文献[4]所给模型进行仿真，分别取地面尺寸为2λm × 2λm(对应图3中文献[4]模型1)和5λm × 5λm(对应图3中文献[4]模型2)，与改进模型仿真结果的对比如图3和表1所示。

图3 场强方向图的对比

图3示出了改进模型与文献[4]模型的场强方向图对比，两者在主瓣仰角上存在差异较大，反映了文献[4]模型地面效应不足的问题，表1说明，改进模型与FEKO模型基本吻合，准确度较高，而文献[4]模型仿真得到的主瓣仰角和半功率波束宽度(Half-Power Beam Width, HPBW)与改进模型有较大差异，误差较大，边元数量和运算时间远远超过改进模型。所以，改进模型比文献[4]模型在仿真性能上有较大提升。

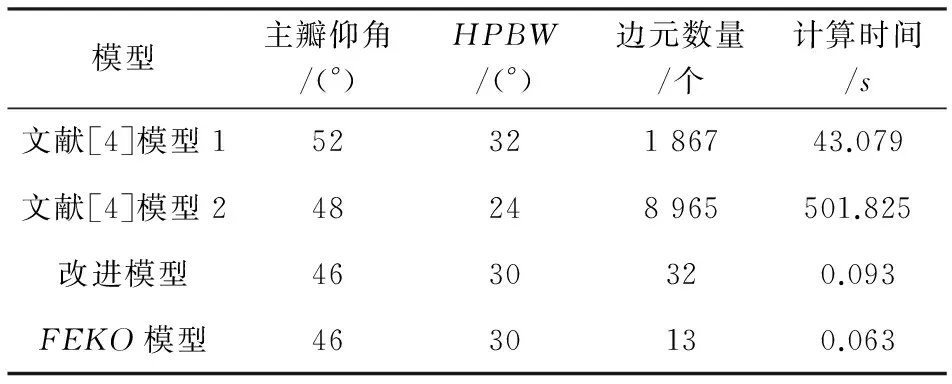
表1 仿真性能对比

注意到馈电边元等效偶极子矩量m沿表面切向的分量对辐射场没有贡献，馈电边元矩量应修正为

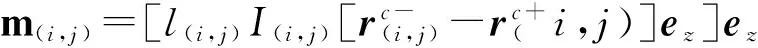
(11)

其中i,j指馈电边元编号。

3 奇异性分析

通过方程(7)计算阻抗矩阵，当边元m和n距离较远时，被积函数在边元域上是连续函数，可用高斯积分来计算。被积函数的奇异点出现在源点和场点重合的情况下，此时，方程(7)可计算为

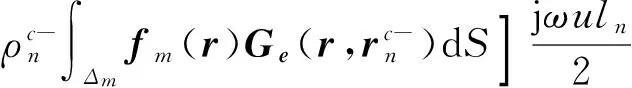
(12)

在满足计算精度要求的条件下，引入9点积分法[13]，式(12)中的积分项可计算为

∫TnGe(r,r′)fn(r′)dS′=

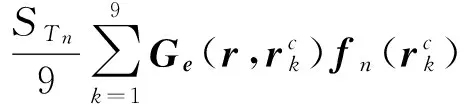
(13)

其中STn表示边元正或负三角形面积。子三角形中心不可能与原三角形中心重合，该方法避免了积分奇异点的出现。文献[14]按照三角形面元进行循环来计算的阻抗矩阵，可提高填充效率。

4 天线辐射性能分析

以10 m鞭天线为例，振子半径0.005 m，工作频率27 MHz，仿真得垂直面(方位角φ= 0°)场强方向图，如图4和图5所示。

从图4可以看出，方向图主瓣在天顶角θ=44°方向上，半功率波束宽度为30°，与文献[15]基本吻合。输入阻抗仿真结果如图6所示。

图6表明，对改进模型仿真得到的输入阻抗和FEKO仿真结果吻合较好 ，达到计算精度的要求，提高了边元利用率并减小了计算时间。

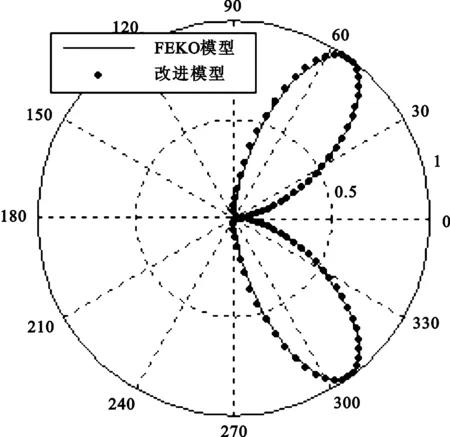
图4 改进模型和FEKO仿真对比

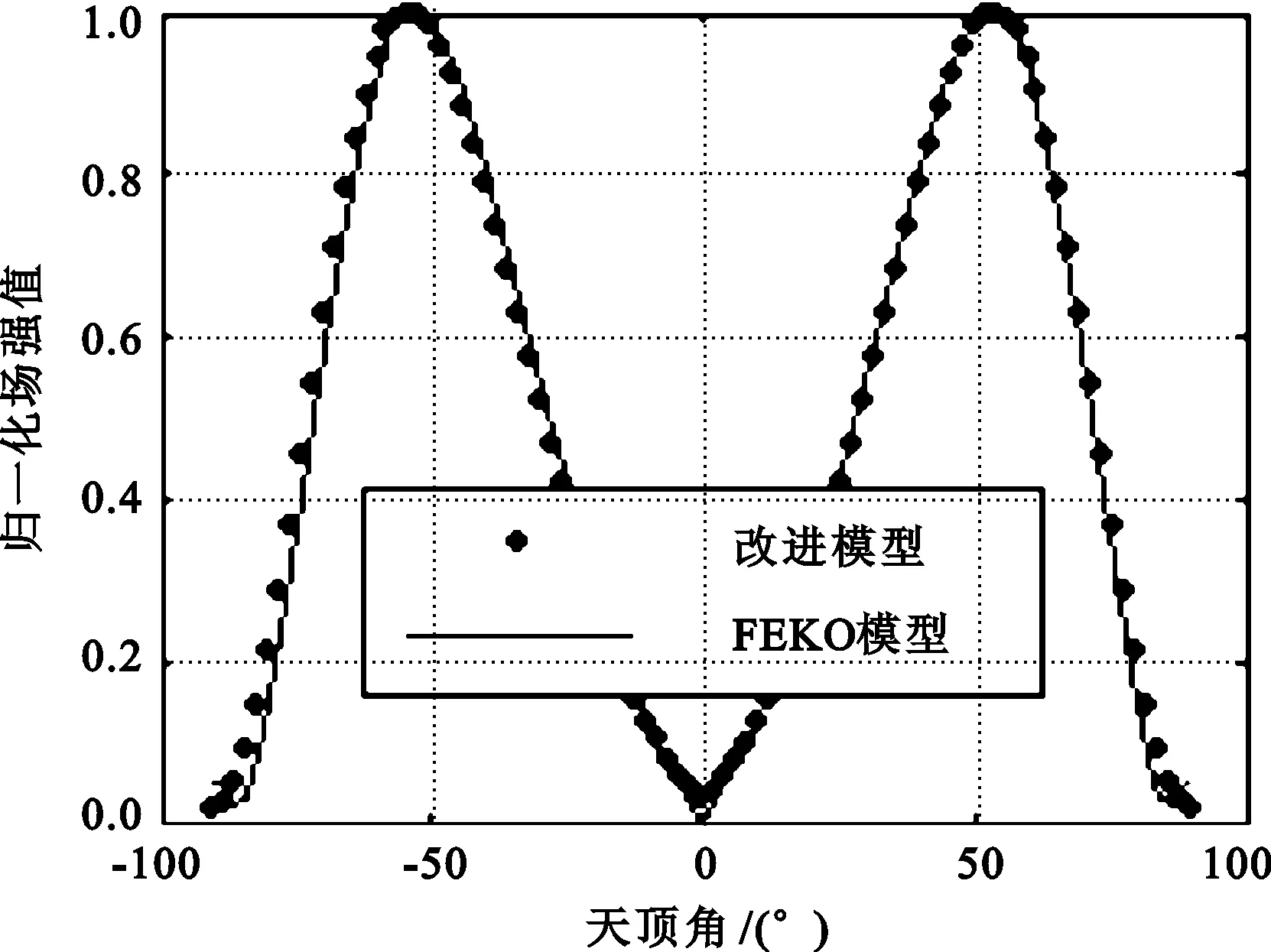
图5 直角坐标系下仿真对比

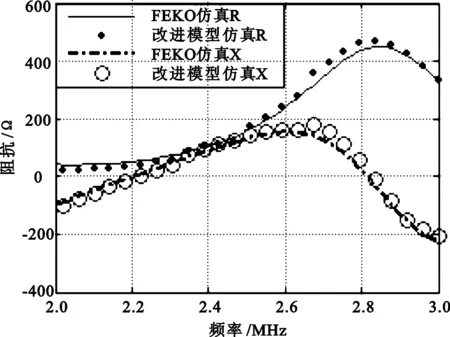
图6 输入阻抗仿真结果比较

5 结 语

针对以自由空间标量格林函数为积分内核的RWG矩量法在求解地面上天线辐射场问题时出现的数据量过大且准确度较低的问题，提出采用辅助三角形改进馈源模型，通过以场型并矢格林函数为积分内核的电场积分方程计算辐射场。对于阻抗矩阵求解中出现的奇异积分，采用9点积分法进行计算。通过计算短波鞭状天线场强方向图和输入阻抗，与FEKO仿真结果作对比，结果表明该方法能够有效减小计算量并提高准确度，从而验证了算法的正确性和有效性。本文采用的处理方法，可应用于双极天线、共形天线等处理的场合。对于并矢格林函数分析分层介质中天线辐射问题将是下一步研究的重点。

[1] Harrington R F. Field Computation by Moment Methods[M]. New York: Wiley-IEEE Press, 1993.

[2] Rao S M, Wilton D R, Glisson A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation,1982,30(3):409-418.

[3] Savage J S, Peterson A F. Quadrature Rules for Numerical Integration over Triangles and Tetrahedra[J]. IEEE Antennas and Propagation Magazine,1996,38(3):100-102.

[4] Sergey N M. Antenna and EM modeling with MATLAB[M]. New York: Wiley Blackwell, 2002: 32-40.

[5] 于涛,尹成友,刘海义.基于RWG-MoM 金属球表面天线的全波分析[J].微波学报,2012,28(1)：23-28.

[6] 杨超,靳伟.基于电磁散射特性的地面特征参数反演[J].西安邮电大学学报,2013,18(4):55-58.

[7] 靳伟,杨超.一种新颖的多频带超材料的仿真研究[J].西安邮电大学学报,2013,18(2):97-100.

[8] 戴振铎,鲁述.电磁理论中的并矢格林函数[M]. 武汉:武汉大学出版社,2005:65-67.

[9] 王长清.现代计算电磁学基础[M].北京:北京大学出版社,2005:153-157.

[10] Balanis C A. Antenna theory: analysis and design[M].2nd ed. New York: John Wiley & Sons Ltd,1997:342-401.

[11] 张青,宗鹏.基于RWG法分析考虑互偶的阵列方向特性[J].现代雷达,2010,32(6)：73-76.

[12] 王生水,毛钧杰,姜永金,等.利用时域电场积分方程分析天线辐射问题[J].电波科学学报,2007,22(5):837-841.

[13] 胡怀宏,孙玉发.一种快速计算阻抗矩阵的有效方法[J].合肥工业大学学报,2011,34(4):617-619.

[14] 韩国栋.矩量法中阻抗矩阵的优化填充技术[J].微波学报,2010(S1):15-19.

[15] Warren L S, Gary A T. Antenna theory and design[M]. 2nd ed. New York: John Wiley & Sons Ltd,1998:60-80.

[责任编辑:王辉]

Analysis of shortwave antenna radiation performance based on RWG-MoM

CHEN Bin1, ZHAO Peng1, YANG Lugang1, YAN Hui2

(1.School of Electrical Engineering, Naval University of Engineering, Wuhan 430033, China;2. Unit 91917 of PLA, Beijing 102100, China)

There would be too much data and little ground effect to calculate the radiation filed correctly when shortwave antenna and ground are all meshed by RWG-MoM. Therefore a new calculation model is proposed in this paper. In this model, some auxiliary triangles are introduced to improve the feed source model, only the antenna radiator is meshed by RWG (RAO-Wilton-Glisson, RWG) edge elements, and the electric field’s dyadic Green’s function integral solution is obtained on perfectly electric conducting flat. The Method of Moment (MoM) is adapted to discrete the Electric Field Integral Equation (EFIE). The singular integral and highly ringing in impedance matrix calculating are analysed and solved by Nine Points Integral Method. Using shortwave whip antenna as example, the field pattern and input impedance are simulated and calculated. Results are in good agreement with the ones calculated by commercial electromagnetic simulation software FEKO and published papers. This new model could reduce the quantity of data and formulated time and increase the calculation accuracy.

method of moment, impedance matrix, dyadic Green’s function, shortwave antenna, radiation performance

10.13682/j.issn.2095-6533.2014.05.019

2014-05-19

陈斌(1975- )，男，硕士，副教授，从事数字通信研究。E-mail：chenbin197501@126.com 赵鹏(1990- )，男，硕士研究生，研究方向为数字通信。E-mail：feixiangzhaopeng@163.com

TN82

A

2095-6533(2014)05-0096-05