基于快速回波算法的雷达仿真

杨瀚涛

(西安邮电大学 教务处, 陕西 西安 710121)

基于快速回波算法的雷达仿真

杨瀚涛

(西安邮电大学 教务处, 陕西 西安 710121)

针对弹载雷达系统仿真速度较慢的问题，提出一种适用于弹载雷达系统的快速回波模拟算法。新算法引入了慢时间的概念，重新推导了雷达回波的表达式，以相参雷达为例,比较了新算法与常规回波模拟算法的运算量，分析了两种算法的等价约束条件。仿真实验结果表明，新算法比常规算法运算量小，并在满足一定误差要求的情形下与常规算法等价。

雷达系统;仿真;快速回波算法;SAR

现代雷达具有高分辨的特点，目标往往要求被认为是多散射点模型。而多散射点在计算回波的过程中，需要大量的乘法和加法运算，消耗大量时间，拖慢了整个仿真过程，成为了提高仿真速度的一大瓶颈，严重限制了雷达仿真的应用范围。如何实现快速仿真工作是目前研究的热点之一。

关于快速回波生成算法方面,文献[1]利用分布式仿真平台，多台机器并行生成一段回波，拼接成最后的SAR回波。该算法通过分布式平台实现，需要多台机器协作，且雷达飞行轨迹已知,但常规单机仿真不能满足上述条件。文献[2]通过FFT实现SAR回波算法，整个流程需要插值，降低了仿真效率。文献[3-5]推导了SAR回波的快速生成算法。该算法是通过二维卷积获得时域回波，需要已知雷达的运行轨迹，且要求雷达天线保持稳定。由于机载、弹载雷达系统，轨迹变化较大，且天线实时调整，因此该算法不能直接应用。文献[6-8]给出了频域及混合域的SAR回波快速算法，但其针对的都为SAR系统，对本文所述系统也不适用。

本文根据文献[3-5]推导弹载雷达仿真系统的回波快速算法，以相参雷达为例，比较了快速算法相对于常规算法的运算复杂度，分析了该快速算法与常规算法等价的约束条件。

1 问题分析

现代高分辨雷达的照射目标看成多散射点模型，散射回波计算需要大量的复数乘法和加法运算，速度往往不尽如人意。

设雷达为脉冲体制，射频发射信号表示为[9]

ut(t)=Aexp(-j2πf0t)×p(t),

(1)

其中A为发射信号幅度，f0为发射载频，p(t)为视频调制脉冲。

设第i散射点的射频回波为

uri(t-τ)=

Ariexp[-j2πf0(t-τi)]×p(t-τi),

(2)

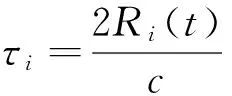
经混频器后输出的视频回波信号为

ui(t)=

(3)

其中ki为混频后第i个散射点的回波幅度。

多散射点的视频回波信号输出表示为

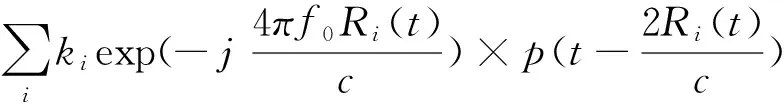
(4)

分析可知，式(4)中的相位项与p(t)的乘法为向量乘法、多散射点回波信号的累加为向量累加，都是比较耗时的步骤。提高这两部分的运算速率，就有可能大幅度的提高仿真效率。

2 算法分析

文献[3-5]给出了快速生成SAR回波算法，该算法通过距离、方位二维卷积生成SAR回波。其中方位卷积运算的前提是雷达运行轨迹已知，且天线稳定。而对于弹载雷达来讲，轨迹不稳且天线实时调整，不能直接引入到弹载雷达回波模拟中来。利用文献[3-5]的分析方法，重新推导弹载雷达回波模拟快速算法。设此时雷达波门宽度为N，目标有P个散射点。

傅里叶变换有如下性质

f(t-τ)=δ(t-τ)⊗f(t)。

(5)

根据式(5)，式(3)的第i个散射点的视频回波可以重写为

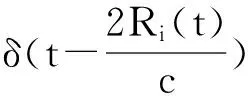
(6)

式(6)卷积的第一部分是一个含有时间t的向量，设长度为N。引入SAR雷达运动模型的“一步一停”[2-5]运动模式，即在产生回波的过程中，认为雷达静止不动的；回波生成后，雷达位置步进；重复生成回波。也就是说，在一次回波产生过程中，雷达到第i个散射点的径向距离Ri(t)认为是不变的，仅与脉冲起始位置有关，可记为Ri(tm)，其中tm为脉冲的起始时间，在SAR中称为慢时间。通过这样的近似，卷积的第一部分转化为tm的函数，不再是t的函数。

对于确定的tm，卷积的第一部分简化为一个复的冲击函数δ(tm)。式(6)可以重写为

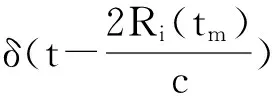
(7)

利用式(7)，重写多散射点的视频回波信号为

(8)

利用卷积分配律，式(8)首先累加卷积的第一部分，最后统一与p(t)卷积得到回波。因此式(8)可分为两部分，第一部分称为散射密度函数，第二部分为视频发射信号P(t)。可以看到散射密度函数的累加为复的冲击函数δ(tm)的累积，相对于前面常规算法的复向量加法，运算量大大减小。

下面首先论证该算法与常规算法等价的约束条件，然后对于两种算法运算量定量分析。最后给出仿真试验验证该算法的相关特性。

3 算法约束条件

设常规算法和快速算法均是以一个脉冲为步长推进仿真，且两者均是仅仿真脉冲内信号。

由于不同位置的散射点，其散射的回波信号相同，只是其相位会随着距离的变化而受到调制，即多普勒效应。本文算法中，雷达以周期Tpr发射脉冲信号，相当于对调制的相位以重复周期Tpr采样，即对多普勒以Tpr采样，而忽略了多普勒在一个脉冲内的变化。

一个脉冲内多普勒的最大相位差为

Δφ=2πfdτ,

(9)

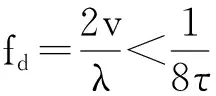
(10)

式(10)表明，一个脉冲内的多普勒变化率远小于脉冲宽度的倒数。频域采样定理很容易解释式(10)。脉冲宽度为τ，频域采样定理要求频域采样间隔[10]

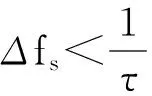
(11)

若一个脉冲内的多普勒变化率可以忽略，就要求多普勒的变化率远小于频域采样间隔，这里取

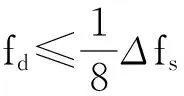
(12)

式(12)代入式(11)可得式(10)。

雷达波长λ=3cm，雷达与目标的径向速度v=300m/s，脉冲宽度τ=1μs。则多普勒为

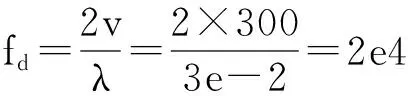
因此该参数设置可满足本文算法的需求。

上面分析可以表明，满足约束条件式(10)，快速算法忽略多普勒在快时间的变化，与常规算法是等价。

4 生成回波运算量比较

为了比较本文快速算法与常规算法的运算量，以相参雷达为例说明。仿真参数如表1所示。设目标散射点有P个，雷达波门采样点数为N，脉冲宽度采样点数为M=τ×fs。微型计算机中，1次乘法的运算量等效于4次加法运算。

4.1 常规算法

常规算法流程如图1所示。

(1)由天线和目标参数计算散射点回波的幅度、相位、延时信息。

(2)利用幅度、相位、延时信息生成多普勒信号，长度为M(仅生成与脉冲等长的多普勒信号)。

(3)多普勒信号与发射信号相乘生成单个散射点的回波信号，需计算M点的复数乘法，等效于4M点加法。

(4)回波累积，需要计算M点加法。一个散射点回波计算共需要5M点加法运算。

(5)重复步骤(1)～(4)，完成多散射点回波信号的计算。

计算回波运算量是5PM点加法。

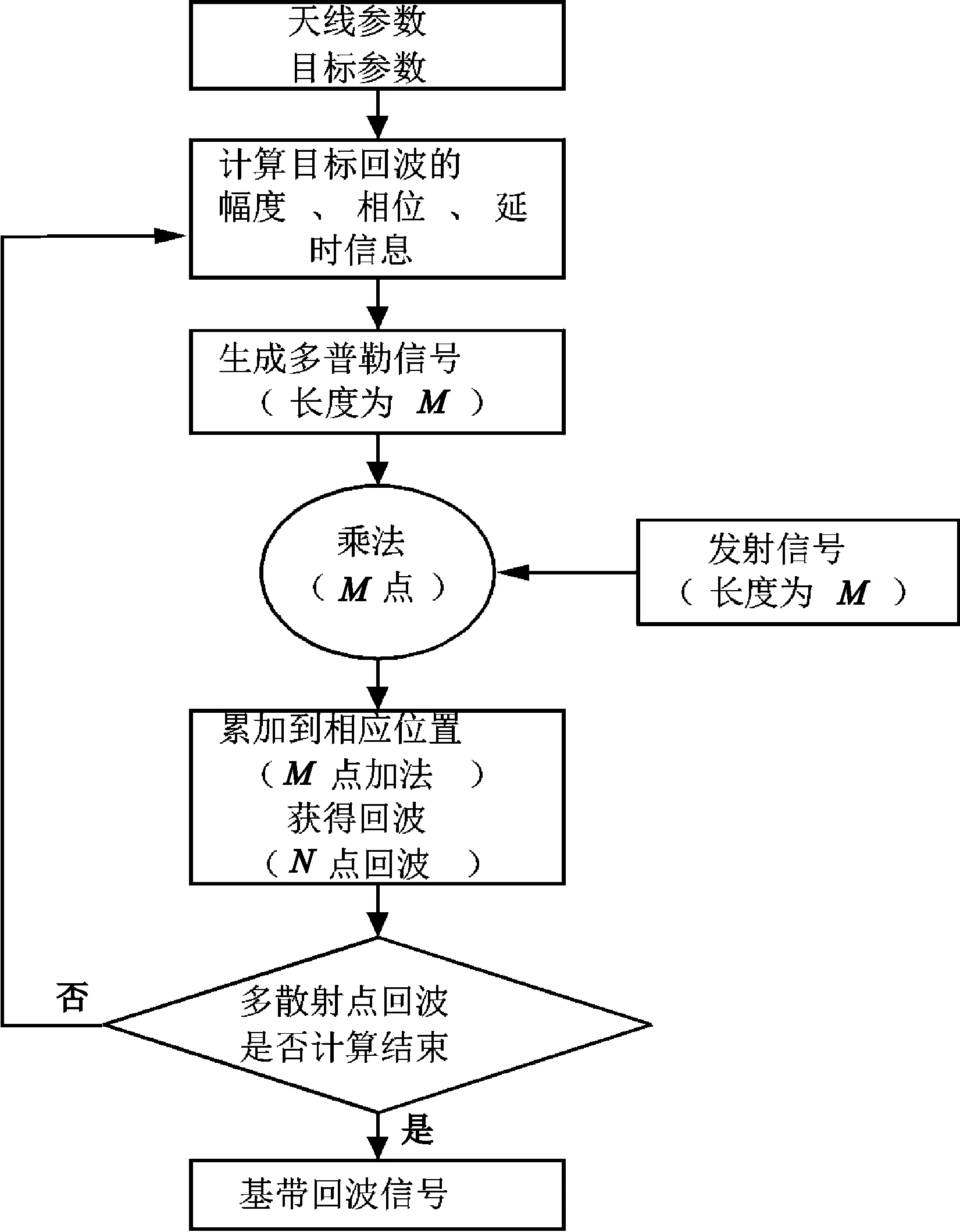
图1 常规算法流程

4.2 快速算法

快速算法流程如图2所示。

(1)由天线和目标参数计算散射点回波的幅度、相位、延时信息。

(2)将其累加到散射密度函数的对应位置，需1点加法，1次乘法，等效于5点加法。

(3)重复(1)(2)多散射点模型，得到散射密度函数。

(4)与发射信号卷积，得到多散射点回波信号，需3次2(M+N)点FFT运算9(M+N)log2(M+N)，一次2(M+N)点乘法，等效于8(M+N)点加法。

计算复杂度

5P+8(M+N)+9(M+N)log2(M+N)。

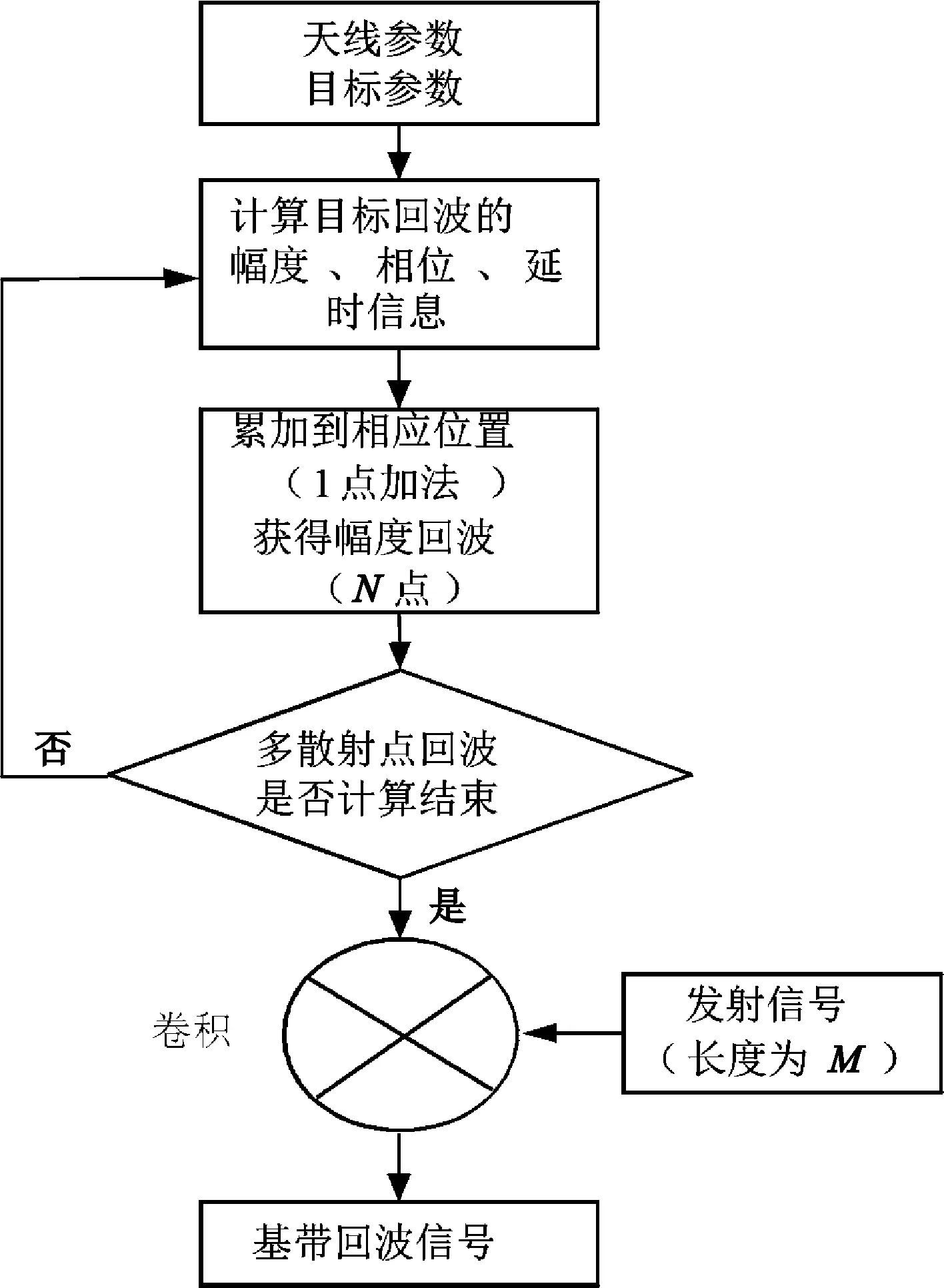
图2 快速算法流程

通过对常规算法和快速算法的比较可以看出：多散射点累加过程中，快速算法5P次加法的速度远小于常规算法的5PM次加法运算。但是快速算法在多散射点累加结束后有一次2(M+N)点的卷积运算，该部分的运算量也相当大的。因此，快速算法不是在任何条件下提高仿真效率，具体在何种情况下该算法可提高仿真效率需要定量分析。

5 生成脉压后信号运算量比较

对于相参雷达而言，回波通过接收机放大后，信号处理机的第一步做脉冲压缩。若将回波生成与脉冲压缩过程结合在一起，则可以进一步提高仿真效率。

5.1 常规算法

常规算法，回波直接做脉冲压缩。运算量为回波模拟和脉冲压缩运算量的累加,即5PM+8(M+N)+9(M+N)log2(M+N)。

5.2 快速算法

快速算法多散射点回波模型为式(8)，其脉冲压缩表示为

(13)

其中s(t)=p*(t0-t)，为发射脉冲p(t)的翻转共轭。

利用傅立叶变换的结合律，式(13)首先计算p1(t)=p(t)⊗s(t)，存储p1(t)，然后卷积散射密度函数。对于式(8)回波模型，快速算法脉冲压缩后回波信号的生成仅将式(8)的p(t)换成p1(t)即可。因此，快速算法的运算量并无增加，为5P+8(M+N)+9(M+N)log2(M+N)。将脉冲压缩与回波模拟结合，快速算法运算量比常规算法减小了约5P(M-1)次，可较大程度的提高仿真效率。因此，若将脉冲压缩与回波模拟结合，快速算法的优势更加明显。

然而是否将脉冲压缩与回波模拟结合，需要根据具体情况而定。若仿真系统为没有脉冲压缩的非相参系统，且散射点数目较多，则仅用快速算法生成回波。若仿真系统为含有脉冲压缩的系统，则快速算法优势明显。

6 仿真实验

实验1 针对散射点数目和数据长度的不同对回波生成效率的影响进行了仿真。仿真散射点最大取P=1 000个，波门采样点N=500点，脉冲采样点取M=τ×fs=100点。

图3给出的是脉冲采样点数固定时，运算量随散射点数目变化曲线。可以看到，回波生成算法：散射点小于121时，常规算法运算量较小；随着散射点数目的增加，常规算法运算量迅速增加，而快速算法运算量变化不大；将回波生成算法与脉冲压缩结合起来，常规算法运算量明显增加，而快速算法没有变化，且常规算法的运算量恒大于快速算法。

图4给出的是散射点为1 000个，运算量随脉冲采样点数的变化。对于回波生成算法：随着脉冲采样点数的增加，常规算法运算量成线性增长，快速算法运算量则是以对数增长。将回波生成算法与脉冲压缩结合起来，同样的，常规算法运算量变化明显，而快速算法没有变化，且常规算法运算量恒大于快速算法。

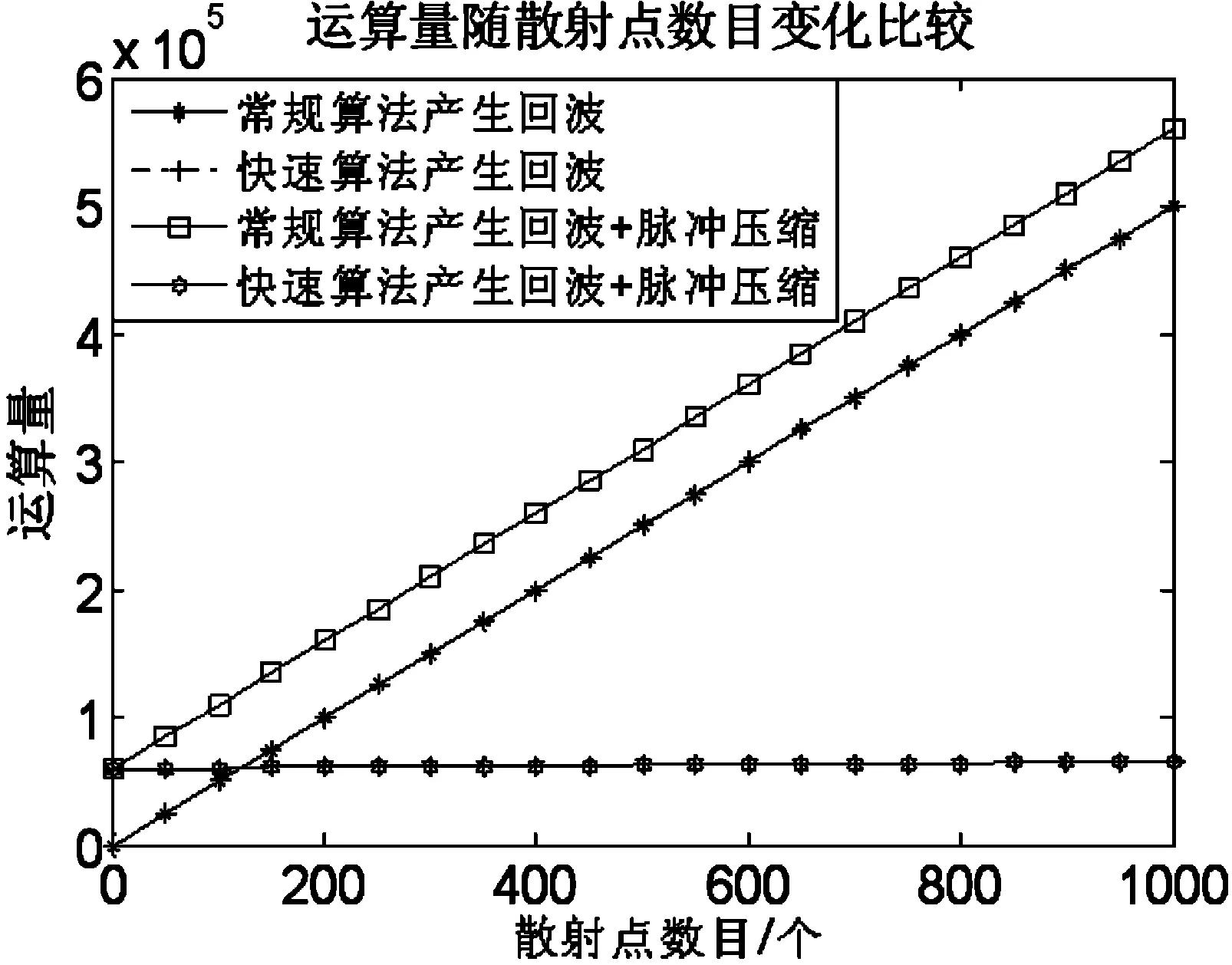
图3 不同算法运算量随散射点数目变化比较

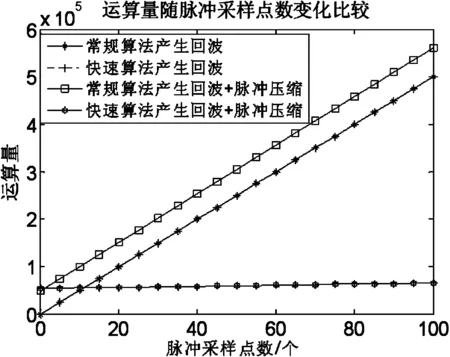
图4 不同算法运算量随脉冲采样点数变化比较

实验2 主要验证快速算法与常规算法的速度差异，以相参雷达为例，通过两种算法分别产生回波，比较两者的差异。这里忽略天线增益。雷达参数如表1所示。

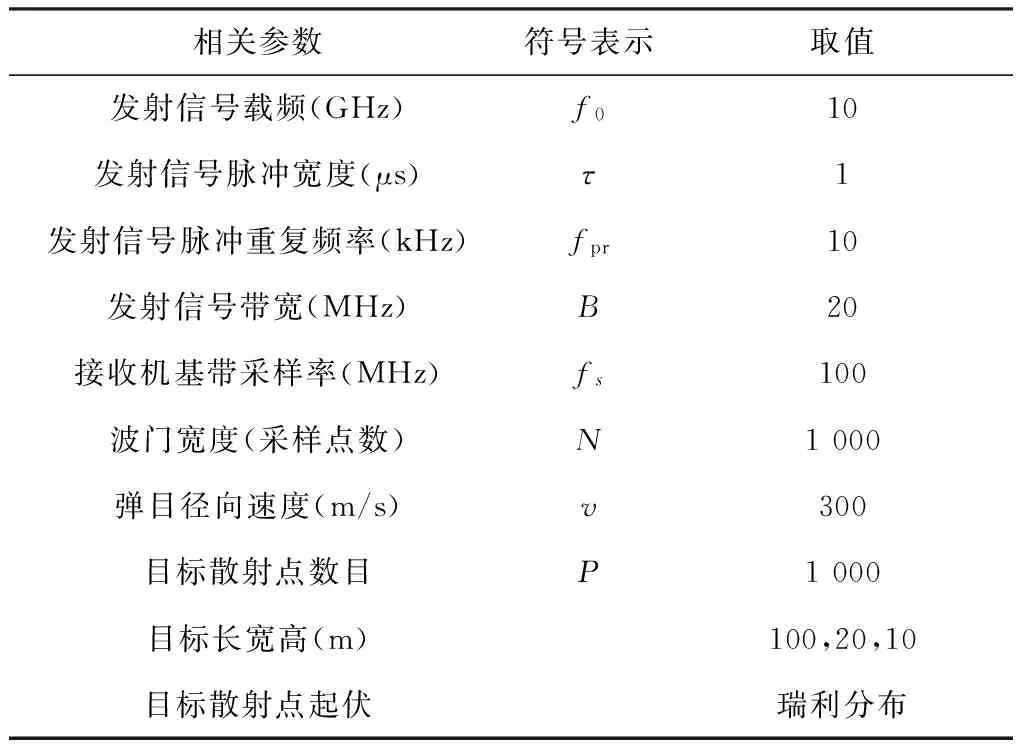
表1 参数列表

图5给出了相参雷达两种不同回波生成算法的结果比较图。图5(a)和图5(b)分别是两种算法的仿真结果，两者几乎完全相同，图5(c)给出的则是将图5(a)和图5(b)做差得到的结果，误差在10-2数量级。

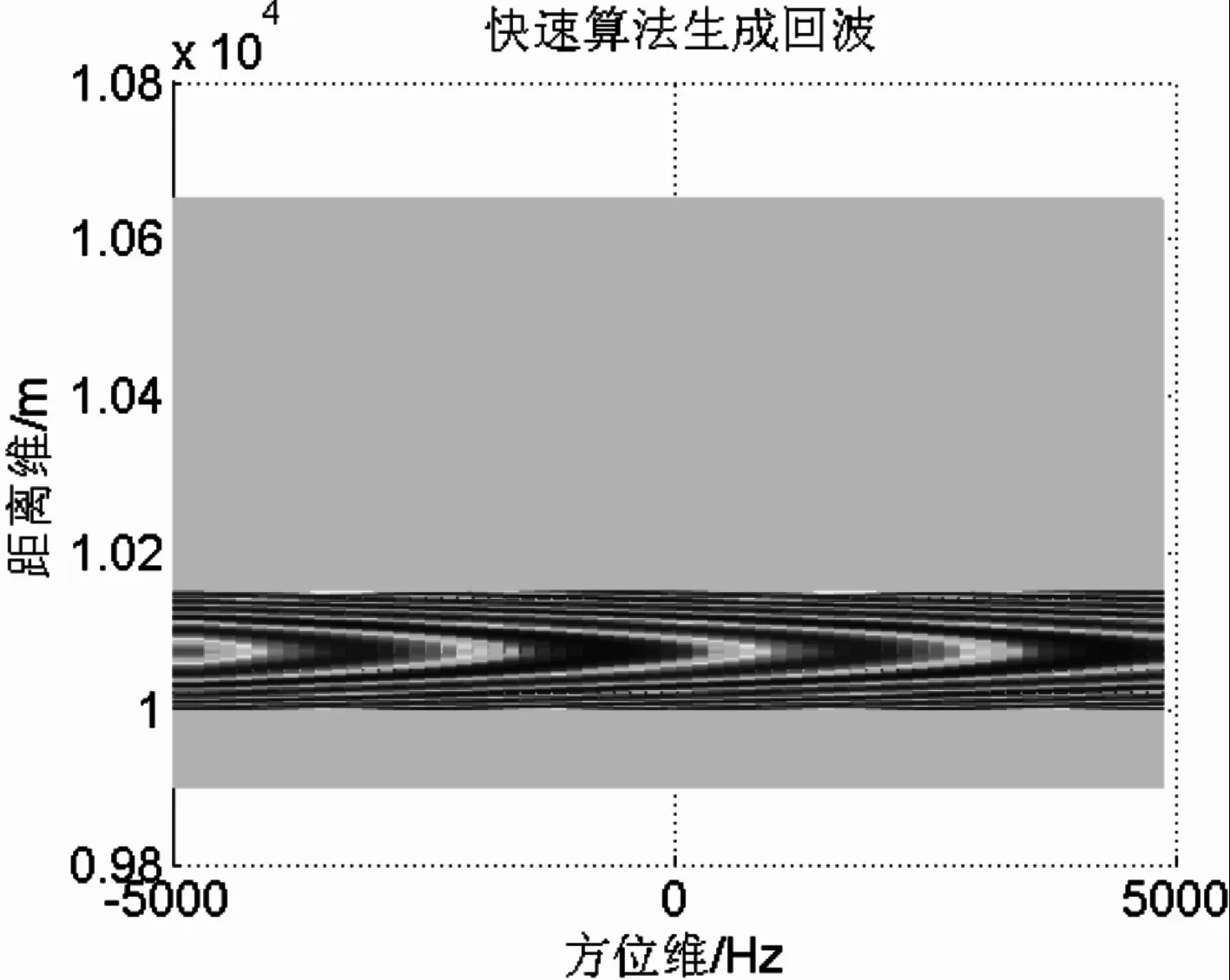
(a)快速算法生成回波

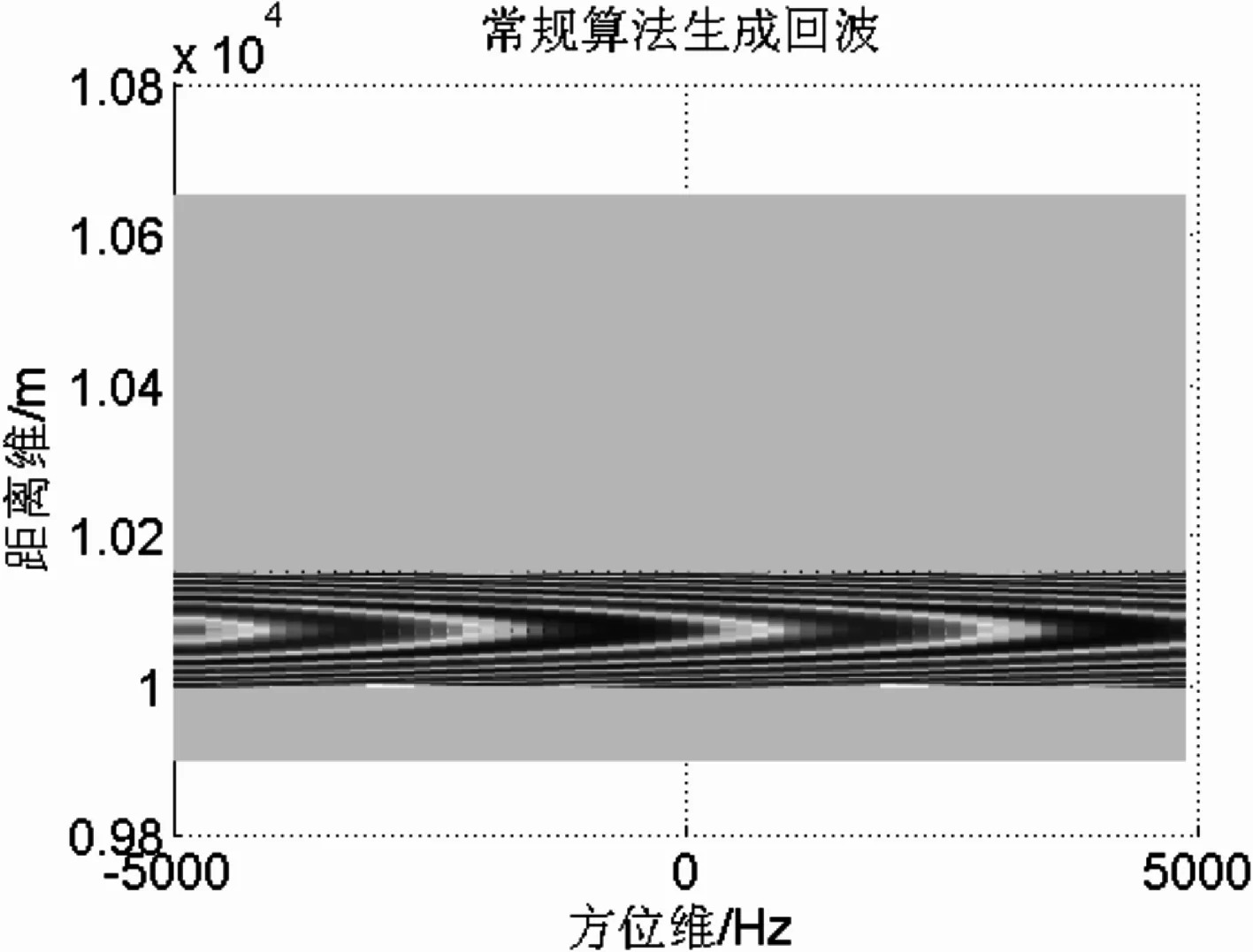
(b)常规算法生成回波

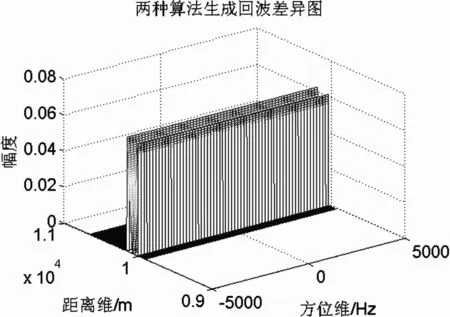
(c)两种算法生成回波差异图

可以看出，本文的快速算法和常规算法在表1的参数条件下，仿真结果在满足一定误差要求的条件下等价。

7 结束语

引入SAR成像回波算法，推导了快速回波模拟算法，分析了该快速算法与常规算法的等价的约束条件，最后通过仿真结果验证了该算法的有效性和正确性。通过分析发现，常规的雷达参数，快速算法和常规算法几乎完全等价。由于该算法的卷积特性，若将脉冲压缩与回波生成结合起来，可以进一步提高仿真效率。

[1] 易予生，刘昕，刘楠，等. SAR回波数据并行化模拟研究[J]. 系统仿真学报， 2008,20(4): 1064-1067.

[2] 黄立胜，王贞松，郑天垚. 基于FFT的快速SAR分布目标回波模拟算法[J]. 遥感学报, 2004,8(2): 128-135.

[3] 何峰，梁甸农，刘建平. 星载双基地SAR空间几何关系和信号模型[J]. 系统工程与电子技术, 2004,26(10): 1328-1331.

[4] 张志勇, 曹治国, 张天序. 一种SAR原始回波数据模拟方法[J]. 信号处理, 1999,15(增刊):77-79.

[5] 宋曦, 周荫清, 陈杰, 等. 一种星载SAR模糊区回波信号仿真方法[J]. 北京航空航天大学学报， 2008,34(2): 144-147.

[6] 韦立登, 李绍恩, 吴一戎, 等. SAR 原始回波信号生成算法的性能比较研究[J]. 电子与信息学报, 2005, 27(2): 262-265.

[7] 汪丙南，张帆，向茂生. 基于混合域的SAR回波快速算法[J]. 电子信息学报, 2011, 33(3): 690-695.

[8] 刁桂杰, 许小剑. 大斜视SAR原始数据的快速模拟算法研究[J]. 电子信息学报, 2011, 33(3): 685-689.

[9] 张居凤, 冯德军, 王雪松, 等. 雷达目标动态 RCS 仿真研究[J].系统仿真学报, 2005, 17(4): 834-837.

[10] 吴大正, 杨林耀, 张永瑞. 信号与线性系统[M]. 北京：高等教育出版社， 2005: 187-192.

[11] 薛爱军，王晓丹，宋亚飞. 基于移动散射点模型的雷达回波仿真及分析[J]. 计算机科学，2013，40(9):201-207

[责任编辑:祝剑]

Radar simulation based on fast echo algorithm

YANG Hantao

(Department of Academic Administration, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

In order to obtain the rapid simulation of the radar system, a new echo algorithm for missile-borne radar system is presented in this paper. A concept of time called slow time is adopted in this new algorithm. A new function of radar echo can then be derived. The constrained equality and the comparison for the operational quantity between the original algorithm and the fast echo algorithm are studied. Simulation results demonstrate the validity of the proposed algorithms. The algorithm can effectively improve the efficiency of simulation.

radar system, simulation, fast echo algorithm, SAR

10.13682/j.issn.2095-6533.2014.05.017

2014-06-16

陕西省国际科技合作基金资助项目(2013KW04-05)

杨瀚涛(1979-)，男，硕士，工程师，从事通信与信息系统研究。E-mail: 37110016@qq.com.

TN958

A

2095-6533(2014)05-0086-06