增强伪自协方差矩阵直接数据域波束合成

陈 杰, 黄友火

(1. 西安航空学院 电气学院, 陕西 西安 710077； 2. 西安电子科技大学 天线所, 陕西 西安 710071)

增强伪自协方差矩阵直接数据域波束合成

陈 杰1, 黄友火2

(1. 西安航空学院 电气学院, 陕西 西安 710077； 2. 西安电子科技大学 天线所, 陕西 西安 710071)

对各天线单元方向图相同且均为全向天线的N元均匀线阵，直接数据域波束合成中已有方法存在着孔径损失，为克服此缺陷，提出一种基于增强伪自协方差矩阵的直接数据域波束合成新方法。将天线阵扩展为一个新的实-虚2N元均匀线阵，建立新2N元阵列的导向向量的伪自协方差矩阵和数据向量的伪自协方差矩阵，通过阵列扩展，增加伪自协方差矩阵的秩和阵列自由度，以消除直接数据域波束合成中已有方法存在的孔径损失。仿真表明，由于新方法没有孔径损失，采用新方法合成的波束增益更高，输出信号的信噪比更大。

波束合成；均匀线阵；直接数据域波束合成；伪自协方差矩阵；自由度

天线的自适应波束合成和波达方向估计在过去几十年被广泛研究,在这一领域有很多研究成果。传统的方法，如子空间法必须计算接收数据的自协方差矩阵[1]，需要大量的接收采样数据和较多的采样时间，并且计算复杂，一般不适合实时应用。为了缩短处理过程的时间，提高处理速度，文献[2]提出了改进的差分遗传波束合成算法；文献[3-5]采用压缩感知的方法完成波束合成；文献[6-11]采用直接数据域(Direct Data Domain Approach, DDDA)方法进行波束合成和波达方向估计，包括波束合成、波达方向估计的算法和各种场合的应用研究。

直接数据域波束合成和波达方向估计方法用接收采样数据的一个或几个快拍建立伪自协方差矩阵，该矩阵具有前述方法中自协方差矩阵的类似功能，但需要的快拍数据却大幅减少，从而降低了计算的复杂度，特别适合于实时处理和自适应处理[6-11]。文献[8]提出了基于伪自协方差矩阵的快速波达方向估计方法，该方法在相干信源的情况下也能得到优良的估计结果，然而前向方法中[8-9]，伪自协方差矩阵构建时会引入天线阵孔径损失，造成阵列的自由度(Degree of Freedom, DOF)降低，从而使阵列可区分的信源数目减少。例如，对N单元均匀线性阵列，伪自协方差矩阵构建时引入的天线阵孔径损失使天线的自由度和可区分的信源数目均不超过(N+1)/2。为了减少天线阵的孔径损失，文献[9]提出了前向-后向法。通过在前向法中的前向矩阵中增加后向矩阵，前向-后向法将天线阵的自由度和可区分的信源数目增加到2(N+1)/3。然而，在传统方法中，N单元天线阵的自由度和可区分的信源数目均为N-1，所以与其相比较，前向-后向法也存在孔径损失。文献[10]提出了直接数据域方法的实数域自适应处理。文献[11]采用时空结合处理提高阵列的自由度和可区分的信源数目，但这种方法需要对接收数据进行二阶处理，计算较为复杂。文献[6-7]采用直接数据域的最小二乘法进行自适应处理，对天线阵的孔径损失并未涉及。

本文提出增强伪自协方差矩阵的直接数据域波束合成的方法。对N元线性阵列，首先按一定的规则将天线阵扩展为一个新的实-虚2N元均匀线阵,并根据其阵元结构建立数据向量和导向向量；然后按直接数据域的方法，建立新阵列数据向量的伪自协方差矩阵和导向向量的伪自协方差矩阵，并合成波束；最后用两个数值仿真例子验证方法的有效性。和传统方法不同，直接数据域的波达方向估计依赖于波束合成技术[8]，因此本文只讨论直接数据域的波束合成方法。

1 增强伪自协方差矩阵的波束合成

考虑一个N元均匀线性阵列，其阵元均为全向天线且方向图相同，相邻阵元的间距为d。假设从各个角度入射的信号为窄带信号，其中心波长为λ。入射信号包括目标信号和其多径信号及干扰。此外，在每个天线单元处还存在热噪声。为了简单明了且不影响问题的分析，假定入射信号共面且为天线阵的远场信号。

首先，在N元均匀线性阵列的左侧放置N个虚阵元，每个虚阵元的特性和实阵元完全相同。实阵元和虚阵元形成一个新的2N元均匀线性阵列，其相邻阵元的间距等于实阵元的相邻阵元的间距d。新的2N元均匀线性阵列称为实-虚均匀线阵。新阵列的阵元排列如图1所示，其中阵元1到N为原实阵列单元，阵元N+1到2N为增加的虚阵列单元。采用新的2N元均匀线性阵列进行直接数据域波束合成可以增加其天线自由度。

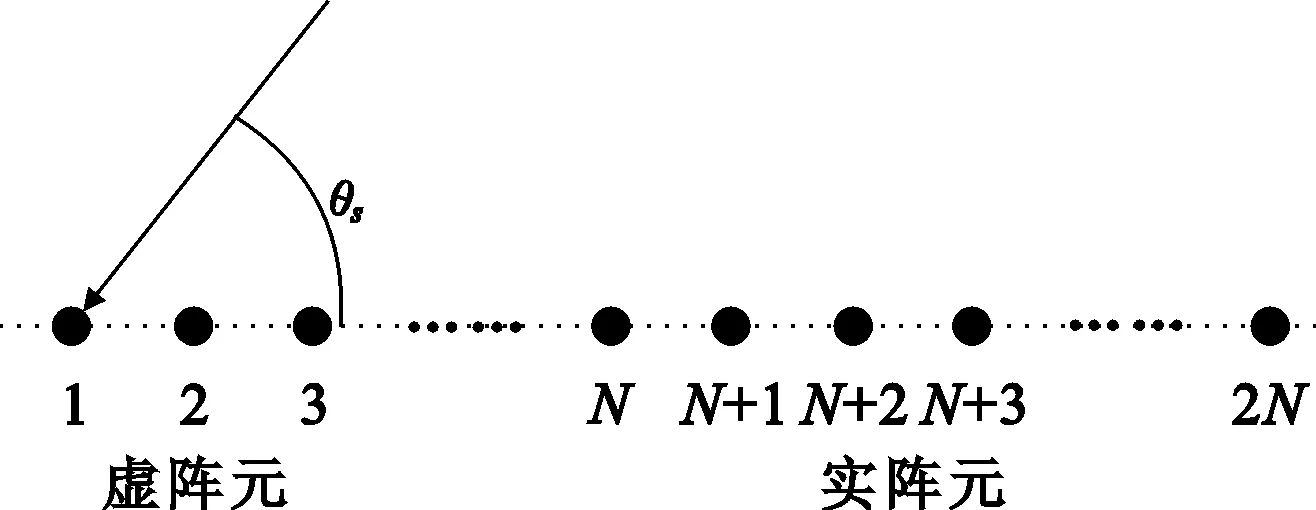
图1 新方法的天线单元排列结构

设实阵列单元在时刻k接收到的数据向量

xr(k)=(xN+1(k),xN+2(k),…,x2N(k))T,

(1)

称为实信号数据向量。虚阵列单元在时刻k的接收数据向量

xv(k)=(x1(k),x2(k),…,xN(k))T=

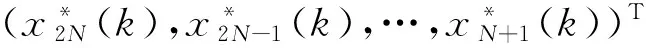
(2)

称为虚信号数据向量。实-虚均匀线阵在时刻k的接收信号数据向量

xa(k)=(xv(k),xr(k))T=

(x1(k),x2(k),…,x2N(k))T。

(3)

设信号的入射角为θs,类似地，分别定义相应实阵列单元的导向向量和虚阵列单元的导向向量为

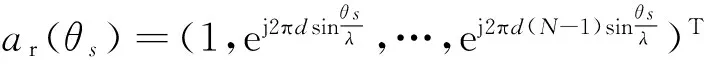
(4)

(5)

其中d表示相邻阵元的间距，λ表示中心波长，则实-虚均匀线阵的所有单元的导向向量可表示为

a(θs)=(av(θs),ar(θs))T=

(a1(θs),a2(θs),…,a2N(θs))T。

(6)

对实-虚均匀线阵采用前向方法形成矩阵，信号数据的伪自协方差矩阵为

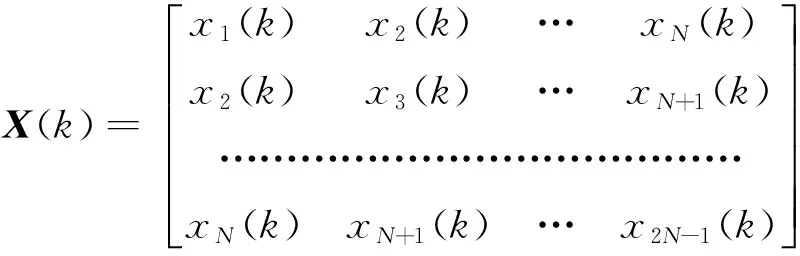
(7)

类似地，可以形成导向向量的伪自协方差矩阵

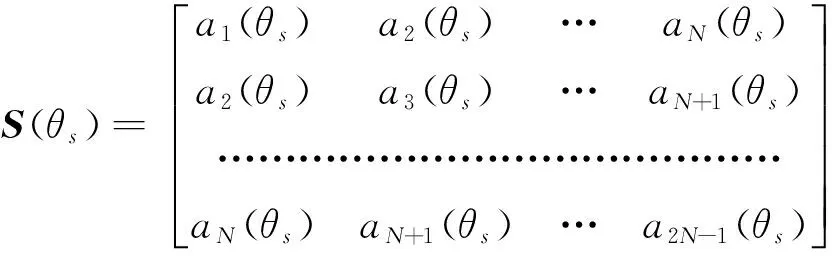
(8)

式(7)和(8)中的信号数据的伪自协方差矩阵X(k)和导向向量的伪自协方差矩阵S(θs)的行列数均为N-1，等于原N元均匀线阵的自由度。此数值和参考文献中的前向和前向-后向伪自协方差矩阵方法的伪自协方差矩阵的秩最大值2(N+1)/3相比有约1/3的提升，所以称为增强伪自协方差矩阵。相对于时-空结合的直接数据域处理方法中采用的二阶处理，新方法对天线接收数据只进行一阶处理，计算的复杂度下降。

设α是目标信号在天线处的信号强度。因为增强伪自协方差矩阵X(k)代表天线单元接收的数据，所以X(k)-αS(θs)只包含热噪声和干扰。如果阵列单元权值向量V可以使热噪声和干扰最小化，则其为期望的权值向量,为此只需使V满足方程[1]

[X(k)-αS(θs)]V=0。

(9)

式(9)可以表示为广义特征值方程的形式，即

X(k)V=αS(θs)V，

(10)

解式(10)可以得到沿θs入射的信号强度。

为了求解式(9)，也可以使其系数矩阵的行列式等于0，即

det[X(k)-αS(θs)]=0。

(11)

式(11)是α的线性方程组。当阵列单元数大于3时求解式(11)相当复杂，故可考虑将其转化为一个块托普利兹系数方程组，以方便求解[1]。首先令

(12)

对于i=1,2,…,2N-2，因为

yi(k)=xi(k)-Z-1xi+1(k)

中不包含来自入射角θs的信号，所以可以得到

(C, 0, 0, …, 0)T，

(13)

其中C为常数，是天线阵列沿方向θs的增益,而Wi(i=0,1,…,N-1)是实-虚均匀线阵的天线单元的权值。

解式(13)得到权值向量后，再由

(14)

可得信号强度α，这就是要求的最终合成波束。

2 仿真实验

用两个例子说明增强伪自协方差矩阵直接数据域波束合成方法的性能,并和原直接数据域波束合成方法比较。两个例子均采用13阵元的均匀线阵，阵元均为全向天线且方向图相同。假设从各个角度入射的信号为窄带信号，其中心波长为λ，相邻阵元的间距d等于入射波中心波长λ的一半。

第一个例子假定目标信号为单位幅度，以θs=60°入射到天线阵；两列按空间分布的干扰群分别沿θ=0°到θ=53°和θ=67°到θ=90°入射到天线阵。两列干扰群中的干扰的入射角在空间等间隔排布，相邻干扰的入射角间隔0.2°，每个干扰都来自点干扰源。由于信号源和干扰源均处于天线阵的远场，所以天线阵的入射波可以用平面波描述。两列干扰波束的幅度用一个等分布随机数产生器产生，其值介于0和1之间。信号和两列干扰波束的相位用另外一个等分布随机数产生器产生，其值介于0和2π之间。天线处还存在热噪声，其幅度和相位也用两个等分布的随机数产生器产生，其幅度介于0和1之间，相位介于0和2π之间，在天线处信号和热噪声的信噪比为10 dB。此外，还有2个50 dB的干扰分别沿θ=15°，θ=30°入射到天线阵，两个45 dB的干扰分别沿θ=46°，θ=72°入射到天线阵。分别用增强伪自协方差矩阵直接数据域波束合成方法和前向-后向法进行波束合成，合成波束的总信噪比(SNR)和入射信号对干扰群的信噪比(Signal to Cluster Interference Ratio, SCIR)的关系如图2所示。

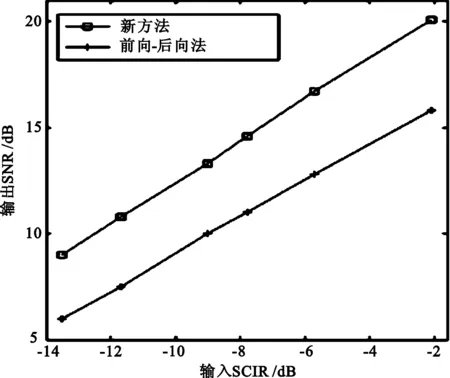
图2 性能对比

如果入射信号对干扰群的信噪比SCIR为-11.7 dB，用前向-后向法合成波束，输出的总信噪比为7.5 dB；但若用增强伪自协方差矩阵直接数据域方法进行波束合成，输出的总信噪比为10.9 dB。两种方法合成波束的总信噪比随入射信号对干扰群的信噪比SCIR增加而增加。

两种方法合成的波束场强信号对比如图3所示,从中可见，新方法的增益更高而干扰的衰减更大。

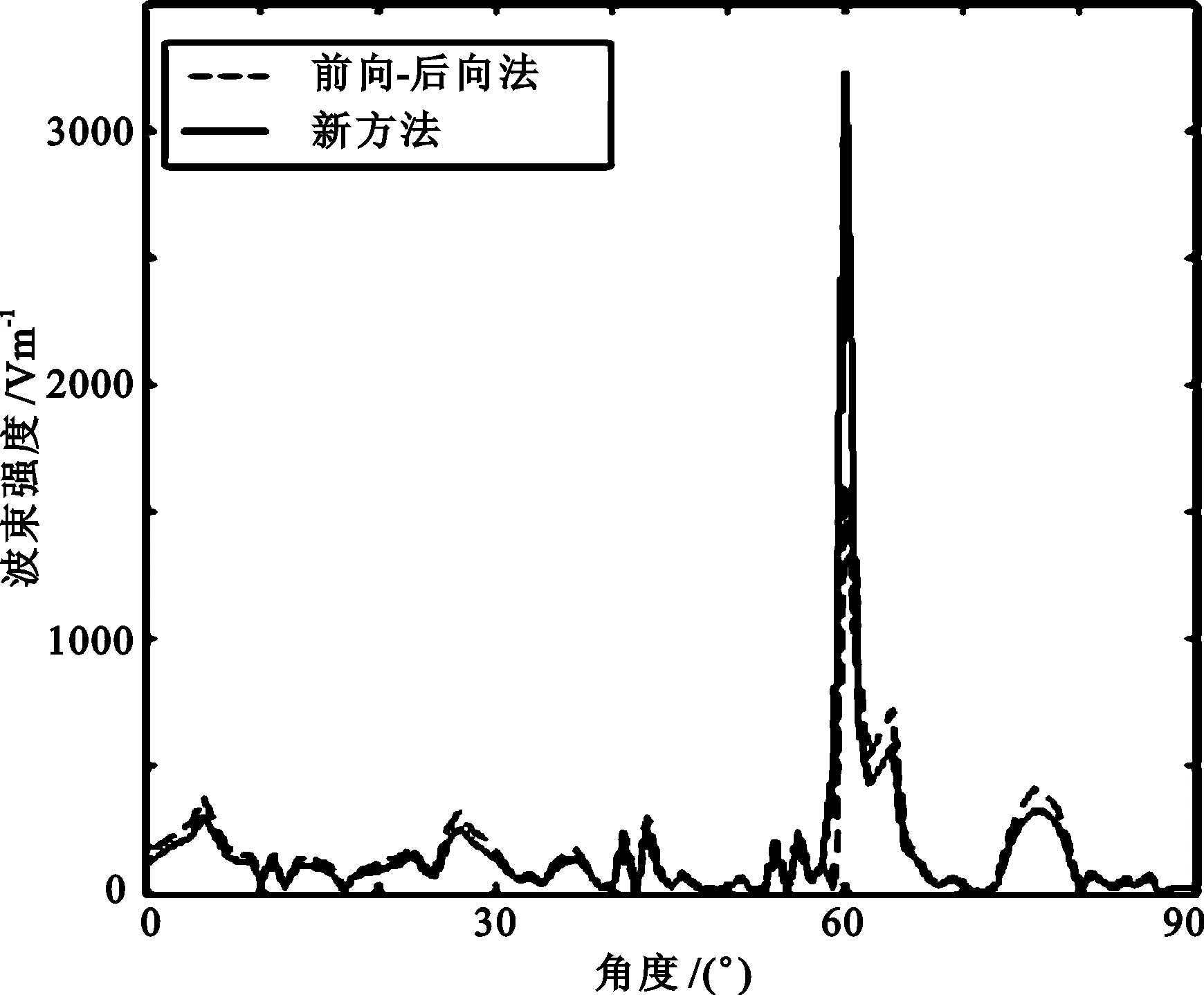
图3 场强信号对比

第二个例子采用和第一个例子相同的天线阵合成波束。目标信号从θs=42°入射到天线阵。4个干扰以不同方向入射到天线阵：56 dB的干扰入射角θ=81°，51 dB的干扰入射角θ=16°，61 dB的干扰入射角θ=26°，48 dB的干扰沿θ=62°入射。两列按空间分布的干扰群分别沿θ=0°到θ=31°和θ=46°到θ=76°入射到天线阵。两列干扰群中的干扰的入射角在空间等间隔排布，相邻干扰的入射方向间隔0.1°，每个干扰都来自点干扰源。此外，天线处还存在热噪声。干扰、噪声和信号的复幅度均用和例1相同的等分布随机数产生器产生。入射信号对干扰群的总信噪比(SCIR)为-6.5 dB，天线处信号和热噪声的信噪比为10 dB。如果用前向-后向法进行波束合成，输出的总信噪比为11.6 dB，而新方法的结果为17.1 dB。

从两个仿真实例可以看到，和前向-后向法相比，新方法合成波束的总信噪比更大，合成波束的增益更大，这正是期望的结果。

3 结 语

采用增强伪自协方差矩阵的直接数据域方法对N元线性阵列进行波束合成。通过将天线阵扩展为一个新的实-虚2N元均匀线阵，其导向向量的伪自协方差矩阵和数据向量的伪自协方差矩阵的秩增加到N-1，比以前的前向和前向-后向法提高了1/3。仿真结果表明，和前向-后向法比较，采用新方法合成的波束增益更高，输出信号的信噪比(SNR)更大。新方法对天线接收数据只进行一阶处理，避免了时-空结合的直接数据域处理方法中采用的二阶处理的复杂计算。

[1] Sarkar T K, Koh J, Adve R, et al. A pragmatic approach to adaptive antennas[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 2000, 42(2): 39-55.

[2] Li Xin, Li Weitian, Shi Xiaowei, et al. Modified differential evolution strategy for antenna array pattern synthesis[J]. Progress in Electromagnetics Research, 2013, 137(2): 371-388.

[3] Oliveri G, Massa A. Bayesian compressive sampling for pattern synthesis with maximally sparse non-uniform linear arrays[J]. IEEE Transactions on Antennas Propagation, 2011, 59(2): 467-481.

[4] Oliveri G, Carlin M, Massa A. Complex-weight sparse linear array synthesis by Bayesian Compressive Sampling[J]. IEEE Transactions on Antennas Propagation, 2012, 60( 5): 2309-2326 .

[5] Chen He, Wang Qin, Fan Rui. Beampattern synthesis using reweighted l1-norm minimization and array orientation diversity[J]. Radioengineering, 2013, 22(2):602-609 .

[6] Sarkar T K, Bhumkar S, Yilmazer N, et al. Non-Statistical Multi-Beamformer[J]. Journal of Signal and Information Processing, 2012, 3 (1): 26-29.

[7] Ren Yanfei, He Haidan, Zhang Yun, et al. An amplitude-only direct data domain least square algorithm of wideband signals based on the uniform circular array[C]//Proceeding of Wireless Communications, Networking and Mobile Computing, 2009. WiCom’09. 5th International Conference on. Beijing: IEEE, 2009: 2271-2274.

[8] Kim J T, Moon S H, Han D S, et al. Fast DOA estimation algorithm using pseudocovariance matrix[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(4):1346-1351.

[9] Wen Zhang, Li Linpei, Wei Ping. Fast direction finding using modified pseudocovariance matrix[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(12):3914-3918.

[10] Choi W S, Sarkar T K,Wang Heng, et al. Adaptive processing using real weights based on a direct data domain least squares approach[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(1): 182-191.

[11] Kim K J, Sarkar T K, Wang Heng, et al. Direction of arrival estimation based on temporal and spatial processing using a direct data domain (D3) approach[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(2): 533-541.

[责任编辑:王辉]

Novel direct data domain approach beamforming using enhanced pseudocovariance matrix

CHEN Jie1, HUANG Youhuo2

(1. School of Electrical Engineering, Xi’an Aeronautical University, Xi’an 710077, China;2. National Key Laboratory on Antenna and Microwave Science, Xidian University, Xi’an 710071, China)

For a uniform linear array withNisotropic omni-direction antenna elements, an enhanced direct data domain approach (DDDA) beamforming is presented to reduce aperture losses in the former DDDA method. In this new method, the array is firstly extended to a new real-virtual uniform linear array with 2Nelements. The pseudocovariance matrices of the data vector and the steering vector of the new 2Nelements array are then formed. By expanding the array, the rank of pseudocovariance and the degree of freedom of the array are all increased to reduce aperture losses of the past DDDA method. Simulation results illustrate the higher output signal to noise ratio can be obtained due to no aperture losses in the new method, and the beam formed by the new method has the higher gain.

beamforming, uniform linear array (ULA), direct data domain approach (DDDA), pseudocovariance matrix, degree of freedom (DOF)

10.13682/j.issn.2095-6533.2014.05.016

2014-05-14

国家自然科学基金资助项目(60871008);陕西省自然科学基金资助项目(2011K09-16)

陈杰(1974-)，男，博士，讲师，从事天线和微波研究。E-mail：chenbinglin88888@163.com 黄友火(1972-)，男，博士，讲师，从事天线和微波研究。E-mail：yhhuang@mail.xidian.edu.cn

TN821+.91

A

2095-6533(2014)05-0082-04