一种面向打印的低维光谱空间构造法

王 莹, 王忠民, 翟社平

(西安邮电大学 计算机学院， 陕西 西安 710121)

一种面向打印的低维光谱空间构造法

王 莹, 王忠民, 翟社平

(西安邮电大学 计算机学院， 陕西 西安 710121)

基于Kubelka-Munk混色理论模型，对其光谱吸收散射比空间进行线性修正，对光谱反射率空间进行正态化处理，并在两种空间之间建立经验变换，之后利用非线性优化技术和主成分分析方法，得到一个保持打印基色光谱特性的低维空间，将光谱反射率数据变换至该空间，以实现针对彩色打印的多光谱数据降维。实验结果表明，新方法能使低维空间数据保持高维光谱空间数据的最主要信息，克服传统主成分分析法导致重建光谱超出光谱数据范围的缺陷。和主成分分析法相比，新方法的色度精度、光谱精度以及同色异谱指数三个评价指标都有提高。

多光谱图像；Kubelka-Munk混色理论模型；非线性优化；主成分分析

对场景高质量的图像采集与输出日益成为科技和商用追求的目标。随着多通道相机与超四色打印机的发展和普及，多光谱图像越来越受到人们的重视。利用多通道相机采集场景图像，通过光谱反射率重建技术即可获得多光谱图像，因此多光谱图像的数据为源场景的光谱反射率。该类图像主要用于源场景在不同观察环境下的精确再现，目前在艺术作品分析与修复[1-2]、医学[3-4]、军事目标图像采集与分析等领域已获得广泛应用。

多光谱图像不同于传统RGB三通道的色度图像，它是利用窄带滤色镜，在可见光波长范围内对场景反射光进行采样，通常在380nm到730nm之间间隔几纳米，因此图像数据维数高，这导致在进行显示器显示、打印机输出等硬拷贝设备再现时，对图像的处理难度高、计算耗时长、所需存储空间大。所以建立一个低维空间，将高维光谱反射率图像数据降维至该空间，然后对降维后的图像进行处理，成为多光谱图像硬拷贝设备再现的重要一环。

目前针对多光谱图像进行降维的方法主要有非负主成分分析法[5]、WSPCAplus法[6]、主成分分析降维法[7-8]、LabPQR空间法[9]等，这些方法都是在主成分分析(Principal Component Analysis, PCA)法的基础上，将光谱反射率降维至一个6维空间。但光谱反射率空间为非正态空间，使用主成分分析法导致降维不稳定，低维数据并不能真正表示高维光谱的最主要信息。此外，在使用经典主成分分析法降维时，从低维数据重构高维数据往往导致高维光谱反射率超出范围[0,1]。当光线照射到物体表面时，反射辐通量与入射辐通量之比就是光谱反射率，因此图像的光谱反射率是一个比值，且为正，这使不在区间[0,1]的反射率数据失去了物理意义。

本文针对多光谱图像的打印应用，在Kubelka-Munk混色模型基础上，提出面向打印的低维光谱空间构造法，用以实现多光谱数据的降维。新方法对Kubelka-Munk模型中的吸收散射系数比空间进行修正，并对源光谱反射率空间进行正态变换，用以提高降维空间的线性性及正态性；并用修正后的空间进行降维变换，以提高多光谱图像的降维精度。

1 理论概述

1.1 Kubelka-Munk混色理论模型

场景物体受到光线照射后会产生反射与吸收，反射辐通量与吸收辐通量相关[10-11]。

假设在可见光波段范围内，总的采样数为h,场景物体在第i(i=1,2,…,h)个采样波长上对光的光谱吸收系数为ki，对应的光谱散射系数为si，则光谱反射率在各波长上的反射系数可表示为光谱吸收系数ki与散射系数si的比值的函数，且吸收与散射系数比和基色颜料的浓度成近似线性关系。另设混合色在第i个采样波长上的光谱吸收系数为Ki，光谱散射系数为Si，那么，由相应的基色颜料混合形成混合色的混色公式可表示为

(1)

其中cj表示基色颜料的浓度，n表示基色数。光谱反射率与Φi的转换关系可由Kubelka-Munk理论得出。

针对不透明介质作变换

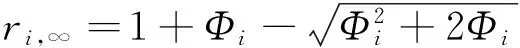
其中ri,∞是不透明介质的厚度为无穷大时的光谱反射率在第i个采样波长上的光谱反射系数，即厚度再增加也不会影响物体的光谱反射率。

材料表面光谱反射率与透明色膜及不透明承印介质底层之间在光学上的相互关系可描述为

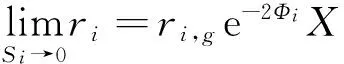
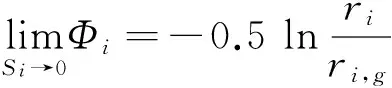
其中ri,g为不透明承印介质的光谱反射率在第i个采样波长上的光谱反射系数，X为色层的厚度。

1.2 主成分分析法

主成分分析法能将高维度数据变换至一个低维特征空间并尽最可能地保持源高维数据的方差，即能用少数变量来表示源数据，同时保持这组数据的最重要信息，是常用的降维方法。

设有由m个h维列矢量形成的矩阵

R=(R1，R2，…，Rm),

其协方差矩阵Σ的秩为u。根据PCA方法，首先求出Σ的所有非零特征值λ1,λ2,…,λu及其对应的特征向量α1,α2,…,αu。利用求得的特征向量形成降维矩阵

V=(α1,α2,…,αu)，

实现源数据的降维，得降维后数据

B=VTR=(β1,β2,…,βu)T，

其中β1称为第一主成分，能反映出源数据的最主要信息，β2称为第二主成分，能反映源数据次主要信息，依此类推，βu为第u主成分。

为实现从低维数据重构高维数据,可取

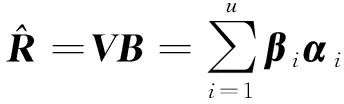
其中β1α1是源数据R的最大近似；β2α2为源数据R的第二大近似；依此类推，βuαu为源数据R的第u近似。

采用主成分分析法降维本质上是使源数据和降维重构数据尽可能地接近[12]，即使得两者的误差尽可能地小。

2 低维光谱空间构造法

文[13]为预估构成一幅多光谱图像的颜料基色的谱密度，从测量得到的多光谱图像的光谱反射率中，通过PCA法得到三个特征向量，对其进行变换获得三个非负向量，以此代表颜料基色的谱密度。一旦计算出基色颜料的谱密度，则可以生成光谱图像的任何谱密度，且其色度误差和光谱误差均较小。重建的谱密度进而可以变换为光谱透射率或反射率。由此得到启示，相对于采用主成分分析法进行降维时以光谱反射率空间作为降维空间，Kubelka-Munk模型中以Φi为特征形成的空间可能更适于作为降维空间，因为光谱吸收散射系数比Φi与基色颜料的浓度成近线性关系，在用有限种基色去合成混合色的应用中，一个线性的高维混色空间更易用一个低维空间去近似。以下将Kubelka-Munk模型中具有m个混合色，且以Φi为特征形成的混色空间记为Φ。

2.1 混色空间与特征向量空间的变换

由PCA法得到的特征向量之间线性无关，这就导致从低维的特征向量空间重构出的高维光谱空间数据有正有负，会出现超出范围[0,1]的现象，这时重构数据并不能真正反映物理颜料的光谱特性；同时，由特征向量空间变换到高维光谱反射率空间的系数矩阵元素也有正有负，不能用于表示真实颜料的浓度。由于颜料的吸收系数与散射系数在各波长上均为正值，所以Φi=Ki/Si的值也为正值，而基色颜料的单位吸收系数在各波长上也均为正，所以对应各基色浓度必然非负。由Kubelka-Munk混色模型可知，任何打印色均是由不同浓度的基色颜料混合而成，式(1)即为混色公式。

根据式(1)可将Φ表示为h×m矩阵

Φ=φC,

(2)

其中h×u矩阵φ是基色颜料的单位吸收散射系数比的矩阵，u×m矩阵C是重建Φ的浓度矩阵。为推导出特征向量矩阵V与矩阵φ之间的相互变换关系，对表征矩阵Φ施加PCA分析，得到其特征值矩阵B和对应的特征向量矩阵V。由

Φ=VB=φC

看出特征向量矩阵V与矩阵φ之间是近线性关系，可表示为

φ=VBC-1=VN,

(3)

其中C-1为C的广义逆。若已知φ，则基色浓度矩阵

C=φ-1VB。

(4)

推导出特征向量与颜料基色的光谱特性之间的变换关系后，可采用非线性优化技术获得基色的光谱特性。

2.2 替代空间的建立

使用PCA法降维，当样本集为非正态分布时，得到的低维空间并不能代表样本的光谱特性。由于不确定样本如何分布，所以PCA法忽略了那些信息贡献率小，但对重构光谱反射率很重要的特征值所对应的特征向量。若样本集为多元正态分布，则可保证从样本集中计算出的特征值与特征向量能用来表征整体采样空间的特征值与特征向量，这等同于在采样空间中进行最优采样，使所采样本的特征向量张成的空间能表征整体样本空间。若一个空间中的样本是多元正态分布，则其中99%的样本应分布于2维椭圆、3维椭圆体和多维超椭球内。在特征向量坐标系内，椭球的轴向长度与其对应的特征值成正比。若空间中的样本分布为非椭球体，则降维后的数据并不能很好地重构出源光谱数据。

Kubelka-Munk混色模型在推导时有两个假设前提:(1) 颜料的膜层在水平方向朝向二维空间蔓延，当光以水平方向通过与之垂直的边缘时，其能量损失与向上和向下扩展时的损失相比非常小，可忽略不计； (2) 仅考察漫射光在色膜中向上下两个方向扩展时，其在色膜中传播时所产生的情况。应用中，往往实际情况与假设前提相违背，这就使得该模型在使用中往往会遇到问题而需要进行改进。

Kubleka-Munk模型本身仅是着色过程的近似，真实的材料是向四面八方散射光，这就背离了Kubleka-Munk模型的假设前提。此外，在采用分光光度计进行光谱测量时，仪器的照明光几乎为直光，而并非现实环境中的漫射光。对于吸收光较少的厚膜，在光线照射入色膜不太深之前就被全部辐射了，遵从Kubelka-Munk混色模型。但假如色膜很薄以至于光未能进行充足的散射或光尚未发生散射就已经被全部吸收，这将使实际结果与Kubelka-Munk模型的模拟结果有很大不同，致使Φ空间的线性假设不成立，此时基色颜料的浓度与混合色的吸收散射系数比已经不再是线性关系，这些均给式(3)带来严重误差。

针对Kubelka-Munk混色模型存在的问题，研究者提出了很多办法来提高混色预测精度，但是这些方法大多较为复杂，在实现时主要依靠优化技术，为使精度达到要求，需设置较多的优化参数。

为了解决Kubelka-Munk混色模型和PCA法自身在使用时所产生的问题，基于Kubelka-Munk混色模型中的Φ空间，建立一个类似的线性光谱吸收散射系数比空间，以该空间替代Φ空间,建立关于基色颜料光谱特性φ的线性变换，将该空间记为Ψ空间。对新空间的推导与对Φ空间的推导一致，不再赘述。针对多光谱降维，需要建立一种针对Ψ空间与光谱反射率空间的变换关系。

(1) 由于样本正态性是影响光谱降维稳定性及精确度的重要因素，因此该变换要能够将非正态分布样本集转换为正态分布样本集，而对正态分布样本集的变换要求仍然能保证样本的正态分布特性。

(2) 对正态变换后的矩阵进行降维，能够获得一个与颜料基色光谱特性相对应的低维空间。

(3) 针对打印输出，在所建立的低维空间中，标量相乘与矢量相加能够描述减色成色原理，即打印及印染成色原理。

为满足上述特性要求，在实验基础上总结得到经验变换

Ψ=a- norm(R),

(5)

其逆变换为

norm(R) =a-Ψ,

(6)

其中Ψ表示新建立的线性空间，该空间数据符合正态分布。a为变换补偿矩阵，主要用于减小Kubelka-Munk混色模型的假设前提与实际不符时所产生的线性误差。a矩阵从样本集中通过优化方法求得，优化的目标函数为样本集与通过PCA法得到的低维空间中重构的光谱的均方根误差。R表示源光谱反射率数据，norm(R)表示对R施加正态变换。

式(5)要满足前述变换特性，必须具备三个条件。

(1) 补偿矩阵a为常量矩阵，norm(R)为对R进行正态变换，结果为正态分布，因此两者相加结果仍符合正态分布。

(2) 新空间Ψ是吸收散射系数比空间Φ的替代，也是关于φ的线性空间，可将其分解为特征值矩阵和特征向量矩阵的乘积。特征向量空间是一个低维空间，可取其维数与颜料基色的个数相同。

(3) 采用非线性优化技术对Ψ空间降维，将其变换到一个低维空间，其光谱特性与颜料基色的光谱特性一致，因此在利用超四色打印对多光谱图像输出时，颜料基色的光谱特性可用Ψ空间降维后形成的低维光谱空间的光谱特性φ近似表示。

2.3 基于替代空间的多光谱图像降维算法

建立Ψ空间后，可在Ψ空间上实现多光谱图像的降维。具体算法分为如下3个步骤。

(1) 对于任意一幅多光谱图像，利用式(5)，首先对图像的光谱反射率数据进行正态变换，进而变换到Ψ空间。

(2) 通过式(3)，对Ψ空间数据采用主成分分析法，得到特征向量矩阵V及特征值矩阵B，并利用非线性优化技术，得到非负特征向量矩阵φ，作为对颜料基色的光谱特性的近似，并用φ张成低维的光谱空间。

(3) 根据非负特征向量矩阵φ，利用式(4)，将光谱反射率数据变换为打印颜料的基色浓度矩阵，作为光谱反射率的降维数据，从而实现了多光谱图像面向打印的数据降维。

从低维的浓度数据重构高维光谱反射率数据的过程分为以下3个步骤。

(1) 利用式(2)，计算得到Ψ空间数据。

(2) 利用式(6)，得到正态分布的光谱反射率数据。

(3) 对上述数据实施正态变换的逆运算，获得重建的光谱反射率数据。

3 实验验证

为验证算法的有效性，实验中对超四色打印机HP designjet 130nr的色空间进行采样，生成实验样本集。130nr为C(青)、M(洋红)、Y(黄)、K(黑)、c(浅青)、m(浅洋红)6通道打印机；光谱测量设备为GretagMacbeth SpectroScanT分光光度计，测量值为光谱反射率，该设备在380 nm到730 nm波长范围内每隔10 nm进行采样，可取得36维光谱反射率，实验选择400 nm到700 nm谱段内的31维光谱反射率数据。实验中的样本集是在130nr的 CMYKcm空间中，每个色轴上均匀划分5级，将各个色轴上的分级数据进行组合，然后对组合得到的色块进行打印，采用分光光度计进行测量，得到15 626个样本。实验中，非正态分布的样本集到正态分布样本集的变换采用Box-cox变换族中的平方根变换。

实验针对超四色打印色空间中的15 626个样本，分别采用PCA法及新算法进行仿真。对降维结果分别从色度、光谱及同色异谱指数三方面予以评价。

对色度精度的评价，需要将多光谱图像变换至色度图像，在此不妨采用CIELAB均匀颜色空间的标准色差公式ΔEab进行评价，其定义为

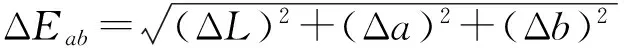
其中L、a、b分别表示CIELAB空间色度值的三个分量，可由光谱反射率与光照的光谱功率分布及观察者色匹配函数积分计算获得。

光谱精度评价采用均方根误差ERMS公式，定义为

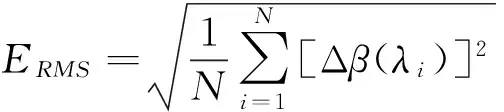
其中N为高维光谱空间的维度，Δβ(λi)为在波长λi处，由低维空间重构的高维光谱反射率与源光谱反射率的误差。

同色异谱指数是指同色异谱对在改变光照情况下的色差大小，实验中将光照从D65变换为A，采用ΔEab进行衡量。

表1给出采用两种方法，将光谱反射率样本降维至6维空间的平均误差统计结果。由表1可知，新算法在三个评价指标上明显优于经典主成分分析降维法。

表1 PCA法与新算法的实验结果比较

图1给出实验样本集中的10个样本采用两种方法的降维效果比较。图1(a)为源光谱反射率曲线，图1(b)为采用PCA法降维后重构的光谱反射率曲线，图1(c)为采用新算法降维后重构的光谱反射率曲线。从图1可以看出，采用PCA法重构的光谱反射率，有超出范围[0, 1]的现象，这使得重构光谱失去了光谱反射率的物理意义。此外，对于波长大于650 nm的光谱，PCA法对源光谱的模拟明显变差，而新算法基于Kubelka-Munk理论模型，利用光谱吸收散射比空间的线性特性及光谱吸收系数和散射系数均为正数的特点，使重构光谱数据保持在 范围内，可用于表征光谱反射率的真实特性。对于波长大于650 nm的光谱，通过新算法重构的光谱，对源光谱的模拟远远优于PCA法。

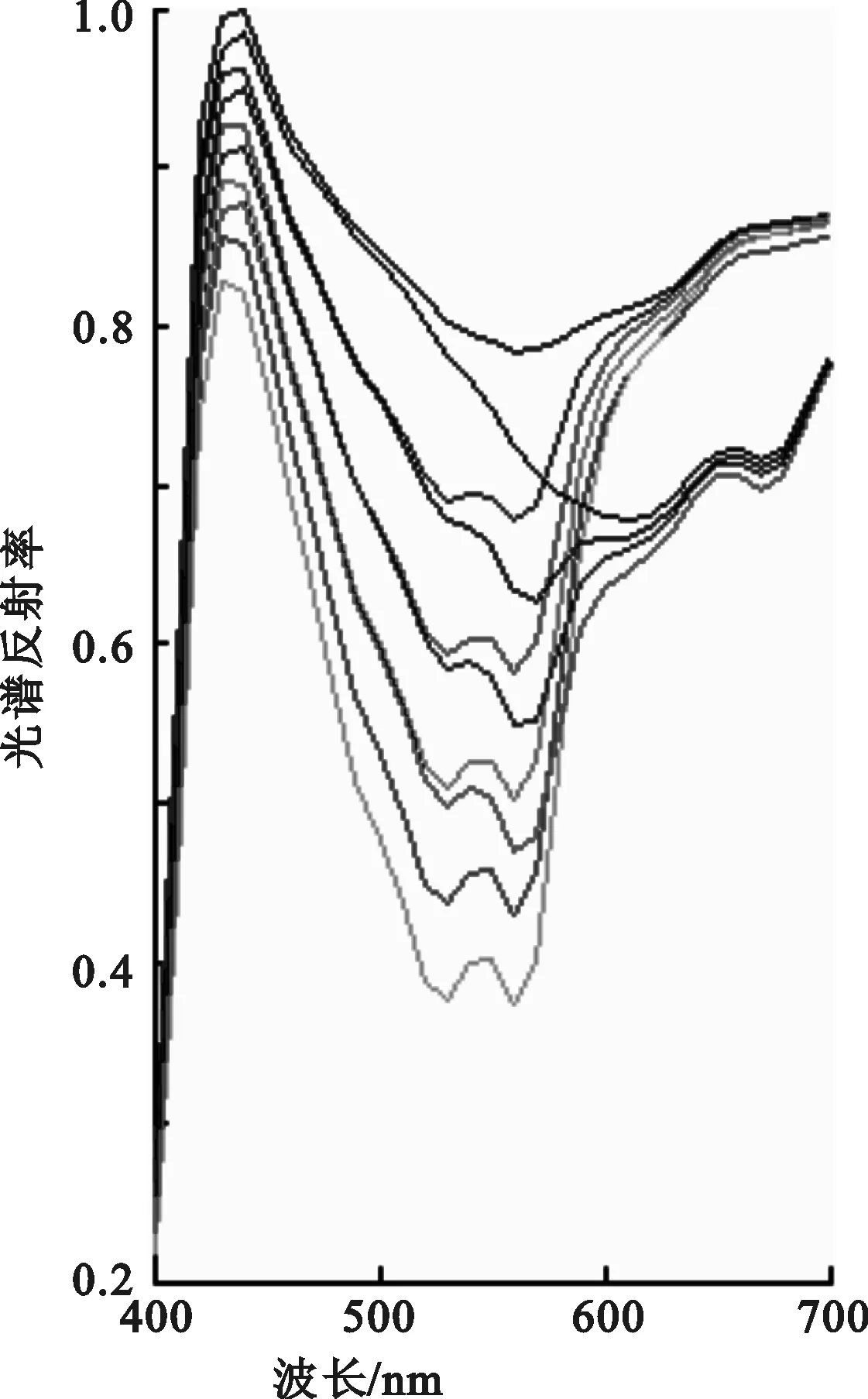
(a) 源光谱

(b) PCA法重构光谱

(c) 新算法重构光谱

图1 源光谱反射率与重构光谱反射率对比

4 总结

针对多光谱图像维度高导致图像打印输出困难的问题，提出一种构造低维光谱空间的方法，并将图像的光谱反射率变换至该空间，实现了多光谱图像的降维。

新方法通过采用Kubelka-Munk混色理论模型，并结合主成分分析法，利用光谱吸收散射比空间为颜料基色浓度的线性变换这一特点，用光谱吸收散射比空间代替光谱反射率空间作为降维空间，提高了降维过程的线性性。

针对Kubelka-Munk模型的局限性，建立了一个新的线性空间。新空间通过引入补偿矩阵，显著缩小了PCA及Kubelka-Munk模型实际应用时所带来的误差。

在将光谱反射率变换至新空间时，首先对光谱反射率进行正态变换，保证了线性降维的稳定性，使得低维空间数据能保持高维光谱空间数据最主要信息。

此外，新方法克服了传统主成分分析法导致重建光谱超出光谱数据范围的问题。与主成分分析法相比，新算法有效降低了多光谱图像降维的误差，从而提高了彩色打印的精度。

[1] Sitnik R, Krzeslowski J, Maczkowski G. Archiving shape and appearance of cultural heritage objects using structured light projection and multispectral imaging[J]. Optical Engineering, 2012, 51(2): 021115-021123.

[2] Berns S R, Chen Tongbo. Practical total appearance imaging of paintings[C]//Proceedings of IS&T. Denmark Copenhagen: Wiley, 2012: 162-167.

[3] Bouzid M, Khalfallah A, Bouchot A, et al. Automatic cell nuclei detection: a protocol to acquire multispectral images and to compare results between color and multispectral images[C]//Proceedings of SPIE, Imaging, Manipulation, and Analysis of Biomolecules, Cells, and Tissues. USA California San Francisco:SPIE, 2013: 85871-85881.

[4] Jakovels D, Kuzmina I, Berzina A, et al. Noncontact monitoring of vascular lesion phototherapy efficiency by RGB multispectral imaging[J]. Journal of Biomedical Optics, 2013, 18(12): 126019-126026.

[5] 王莹, 曾平, 罗雪梅, 等. 一种用于低维光谱空间构造的非负主成分分析法[J]. 四川大学学报, 2010, 42(2):165-170.

[6] 王莹, 王忠民, 王义峰, 等. 面向色彩再现的多光谱图像非线性降维方法[J]. 光学精密工程, 2011, 19(5):1171-1178.

[7] Wu Chongyi, Lee Shunming, Wen Chanhua, et al. Multi-spectral image acquisition system for color spectrum reproduction[C]//Proceedings of CVGIP. Taiwan Kinmen:Mingchuan University Press, 2003: 115-122.

[8] Bakke M A, Farup I, Hardedberg Y J. Multispectral gamut mapping and visualization: a first attempt[C]//Proceedings of SPIE. USA California San Jose: SPIE, 2005, 5667: 193-200.

[9] Derhak W M, Rosen R M. Spectral colorimetry using LabPQR: An interim connection space[J]. Journal of IS&T, 2006, 50(1): 53-63.

[10] Kubela P, Munk F. Ein Beitrag zur Optik der Farbanstriche[J]. Zeitschrift fur Technische Physik (German), 1931,12(5): 593-601.

[11] Kubleka P. New Contribution to the Optics of Intensely Light-Scattering Materials[J]. Journal of the Optical Society of America, 1948, 38(5): 448-457.

[12] 王小刚, 田小平, 吴成茂. 基于压缩感知的图像快速重构去噪算法[J]. 西安邮电学院学报,2012, 17(4):11-14.

[13] Ohta N. Estimating Absorption Bands of Component Dyes by Means of Principal Component Analysis[J]. Analytical Chemistry, 1973,45(2): 553-557.

[责任编辑:瑞金]

Construction of low-dimensional spectral space for multi-ink printing

WANG Ying, WANG Zhongmin, ZHAI Sheping

(School of Computer Science and Technology, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

By correcting coefficient ratio space of the absorption based on scattering of Kubelka-Munk turbid media theory, and exerting a normalization transformation to the spectral reflectance space, a new linear space is created. Then a transformation between the spectral reflectance space and the new space is established. A low dimension spectral space which is consistent with the multi-ink color space is finally achieved by utilizing the nonlinear optimization and principal component analysis. The dimensionality reduction of the multi-spectral image for multi-ink printing is accomplished through the transformation of spectral reflectance to this low dimension space. Experiments show that the data obtained by this new method in the low dimension space can keep the main spectral information of the data in the high dimension spectral space. Furthermore, the new method can overcome the shortcoming brought by the principal component analysis, which is that the spectral reflectance reconstructed from the low dimension space may exceed the range of the spectral data. Compared with the principal component analysis method, this new method can make great improvements in the colorimetric accuracy, spectral accuracy and metamerism index.

multispectral image, Kubelka-Munk turbid media theory, nonlinear optimization, principal component analysis

10.13682/j.issn.2095-6533.2014.06.016

2014-06-05

陕西省自然科学基金资助项目(2012JM8044)；陕西省教育厅科学研究计划资助项目(12JK0733)；西安邮电大学青年教师科研基金资助项目(ZL2011-09)

王莹(1977-)，女，博士，讲师，从事颜色科学及多光谱图像处理研究。E-mail:wangyingjsj@xupt.edu.cn 王忠民(1967-)，男，博士，教授，从事智能信息处理研究。E-mail:zhmwang@xupt.edu.cn

TP391.4

A

2095-6533(2014)06-0080-06