蜗杆传动的可靠性优化设计研究

胡启国,谢国宾，庹 奎

(重庆交通大学 机电与汽车工程学院，重庆 400074)

蜗杆传动的可靠性优化设计研究

胡启国,谢国宾，庹 奎

(重庆交通大学 机电与汽车工程学院，重庆 400074)

将可靠性设计理论与优化设计理论相结合，讨论了在应力及强度服从对数正态分布的情况下，蜗杆传动的可靠性优化设计的问题，建立了蜗杆传动可靠性优化设计的数学模型。通过使用Matlab优化工具箱对该模型进行求解，得出了既可靠又最优的参数值，并从蜗杆传动的可靠度方面验证了此种方法的可行性。结果显示，该方法不仅提高了蜗杆传动设计的效率和可靠度，对解决其他机械优化设计问题同样具有重要的参考价值。

蜗杆传动；Matlab优化工具箱；可靠性

0 引言

在机械设计领域，优化设计和可靠性设计的发展给整个机械设计学科带来了深刻的影响[1]。但优化设计和可靠性设计往往不能同时实现。所以，要使产品既有可靠性要求，又有最优的设计结果，就必须将这两个理论结合起来，即可靠性优化设计方法[2]。可靠性优化设计既保证了零部件的经济效益，又能使其安全可靠的运行。

机械零部件可靠性优化设计问题一般包括三个方面的内容：质量(重量)、成本、可靠度。机械零部件的可靠性优化问题可分为两类：①使零部件的可靠度最大；②使零部件费用(或体积、重量等)最小或性能最好[3]。目前国内外学者对可靠性优化设计方法进行了深入的研究，魏宗平等[4]基于非概率可靠性理论和优化设计方法，提出了机床主轴结构的非概率可靠性优化设计方法。樊立梅[5]提出了把减小斜齿轮体积和提高传动平稳可靠性结合，进行多目标联合优化设计的方法。Tae Min Cho等[6]提出了基于移动渐近线法的可靠性优化设计方法。张伟强等[7]应用摄动法和可靠性设计理论，在基本随机参数的概率特性已知的情况下，对蜗杆传动进行可靠性设计。本文以普通圆柱蜗杆传动为例，在蜗轮轮齿应力及强度均服从对数正态分布情况下，以蜗轮蜗杆体积之和最小作为可靠性优化设计的目标函数，并建立可靠性优化设计的数学模型。

1 蜗杆传动可靠性优化模型

1.1 设计要求

已知输入功率P，输入轴转速n1，传动比i，要求在满足蜗杆传动齿面接触疲劳强度、齿根弯曲疲劳强度的可靠度和几何边界约束的条件下，使得蜗杆传动的结构最紧凑。

1.2 目标函数及设计变量

根据设计要求，使蜗杆传动的结构最紧凑。同时考虑到在蜗杆传动中，通常采用淬硬磨削的钢制蜗杆，而采用贵重的青铜等材料制造蜗轮齿圈，以使传动副具有良好的减磨性、耐磨性和抗胶合的能力。为了节省较贵重的有色金属，降低成本，也常要求蜗杆传动的结构紧凑。故在本文中，可靠性优化设计的目标函数为蜗轮蜗杆的体积之和最小，即

+m2(q-2.4)2(0.9mZ2-L′)]

(1)

式中，B2—蜗轮齿宽,

B2=[m(q+2)-0.5m]sinγ+0.8m;

γ—蜗轮包角的一半，一般取γ=50°;

L'—蜗杆螺纹部分的长度;

L'=(12.5+0.09Z2)m+25。

由式(1)可知，蜗杆的头数Z1、蜗杆的直径系数q和蜗轮的端面模数m决定了蜗轮蜗杆的体积之和，而式中传动比μ一般为给定值，故取设计变量为：

X=[x1,x2,x3]T=[Z1,q,m]T

1.3 建立约束条件

(1)接触疲劳强度的可靠度约束

g1(X)=[RH]-RH≤0

(2)

假设蜗轮轮齿应力及强度均服从对数正态分布。则根据应力—强度对数正态分布的干涉模型可知，可靠度R与可靠度系数ZR有一一对应的关系，故式(2)亦可表示为：

g1(X)=Z[RH]-ZRH≤0

式中Z[RH]的值由给定的可靠度系数[RH]的值查正态分布表得到。接触疲劳强度的可靠度可表示为：

(3)

(2)弯曲疲劳强度的可靠度约束

g2(X)=[RF]-RF≤0

(4)

与(1)同理，式(4)亦可表示为：

g2(X)=Z[RF]-ZRF≤0

式中Z[RF]的值由给定的可靠度系数[RF]的值查正态分布表得到。弯曲疲劳强度的可靠度可表示为：

(5)

(3)蜗杆头数的约束

为提高传动效率，对于做动力传递的蜗杆头数要求Z1=2～4。

(4)蜗轮齿数的约束

对于做动力传递的蜗轮，其齿数一般要求Z2=μZ1=30～80。

(5)模数的约束

对于中小功率的蜗杆传动，其模数要求m=2～18。

(6)蜗杆直径系数的约束

根据蜗杆传动的使用情况，其直径系数一般推荐为q=7～20。

(7)蜗杆刚度的约束

当蜗杆轴啮合部位受力后，将使轴产生挠曲，从而造成偏载，加剧磨损。所以，一般要求蜗杆轴的最大挠度不超过0.01m，即：

(6)

式中，L—蜗杆的支撑跨度，L=0.9d2=0.9mμZ1；

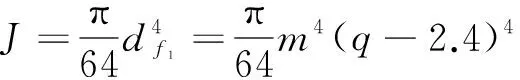
E—弹性模量E=2.06×105MPa

由于材料和结构上的原因，蜗杆螺旋部分的强度总是高于蜗轮轮齿的强度，所以失效经常发生在蜗轮轮齿上，蜗杆很少发生疲劳破坏，所以建立约束条件时不考虑蜗杆轮齿强度的可靠性约束。

2 应用实例

设计某驱动机构上的普通圆柱蜗杆传动，数据处理之后为，蜗轮转速n2=6r/min，输出轴扭矩T2=4.2×105N·mm，工作平稳，齿数比μ=18，压力角α=20°，蜗轮齿圈材料为ZCuSn10P1，接触疲劳极限为σHlim=220MPa，弯曲疲劳极限为σFlim=56MPa，传动效率η=0.83，要求蜗杆传动的工作可靠度大于0.99，最大使用期限8年。

2.1 计算可靠度系数

(1)计算接触应力和弯曲应力的均值及变异系数

蜗轮的接触应力均值计算公式：

(7)

式中，ZE—材料的弹性影响系数，

K—载荷系数；

蜗轮的接触应力变异系数：

(8)

式中，CZE,CK,CT2分别为材料弹性影响系数、载荷系数、输出轴扭矩的变异系数。

蜗轮的弯曲应力均值计算公式：

(9)

式中，mn—蜗轮法面模数；

b2—蜗轮齿根弧长。

蜗轮的弯曲应力变异系数：

(10)

式中，CFt2,Cb2分别为蜗轮圆周力、蜗轮齿根弧长的变异系数。

(2)计算接触疲劳极限和弯曲疲劳极限的均值及变异系数

对于本文所选取的蜗轮，根据参考文献[8-9]，接触疲劳极限的对数标准差SlσHlim=0.1，弯曲疲劳极限的对数标准差SlσFlim=0.2。

对数接触疲劳极限均值

klσHlim=2.326SlσHlim+lnσHlim

接触疲劳极限均值

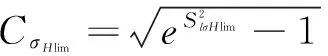
同理

对数弯曲疲劳极限均值

klσFlim=2.326SlσFlim+lnσFlim

弯曲疲劳极限均值

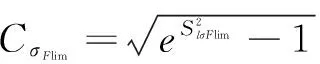
(3)计算接触疲劳强度和弯曲疲劳强度的均值及变异系数

接触疲劳强度的均值及变异系数

式中，ZN—接触疲劳寿命系数；

ZL—润滑油系数；

ZR—表面粗糙度系数；

Zv—速度系数。

弯曲疲劳强度的均值及变异系数

式中，YN—弯曲寿命系数；

Yω—齿根圆角敏感系数；

Yβ—尺寸系数。

(4)计算接触疲劳强度和弯曲疲劳强度的可靠度系数

(11)

(12)

2.2 可靠性优化设计数学模型

目标函数：

非线性不等式约束：

线性不等式约束：

g4(X)=x1-4≤0，g5(X)=2-x1≤0

g6(X)=18x1-80≤0，g7(X)=30-18x1≤0

g8(X)=x3-18≤0，g9(X)=2-x3≤0

g10(X)=x2-20≤0，g11(X)=7-x2≤0

2.3 优化设计模型的求解

MATLAB在由美国的Mathwork公司发布后，就因其功能强大、使用简单、容易扩展而立刻风靡全球。在这个强大的计算平台既可以利用MATLAB优化工具箱(Optimization Toolbox)中的函数，又可以通过对算法编程实现相应的最优化计算。其优化工具箱的序列二次规划算法(SQP)，被公认为最优秀的非线性约束优化算法之一[10]。MATLAB优化工具箱中的fmincon函数使用了SQP算法，求解时可直接调用该函数，fmincon函数的调用格式为：

[x,fval,exitflag,output]=fmincon (fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2, ...)

该优化问题是有3个目标变量，11个约束条件的约束优化问题，应用MATLAB优化工具箱的fmincon函数求解该优化问题。编写目标函数的文件objf.m，非线性约束条件函数的文件nlcon.m。在MATLAB命令窗口中输入变量的初始搜索值和线性约束，并调用优化程序。结果为：

X*= [2.1622 9.1917 4.5270]

f(X*)=1.1701×106mm3

对优化结果进行圆整，取其离散最优解：蜗杆齿数Z1=2，蜗杆直径系数q=9，模数m=5，此时蜗轮和蜗杆的体积为V=1.34×106mm3。

2.4 可靠性优化设计与常规设计的对比

(1)基本参数对比

可靠性优化设计与常规设计的参数的对比结果见表1。

表1 设计参数的对比

(2)可靠度的对比

在闭式蜗杆传动中，其失效形式主要为点蚀或胶合，为证明此可靠性优化设计方法的合理性，本文从蜗轮轮齿接触疲劳强度的可靠度方面与常规设计可靠度进行了对比。设蜗轮转数N=60nt，t=8×300a，寿命系数为

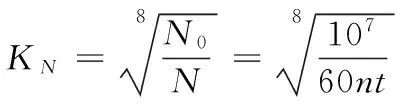
按上述条件及式(11)可计算出可靠度与时间的变化关系，与常规设计可靠度的对比结果见表2。

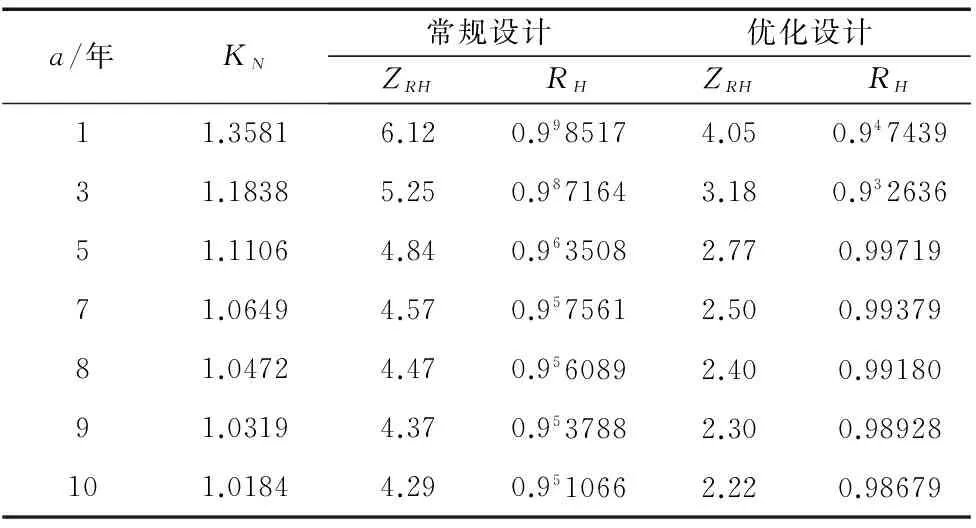
表2 可靠度的对比

注：0.99表示在小数点后有9个9，其他同理。

3 结论

(1)将可靠性设计理论与优化设计理论相结合，并采用MATLAB优化工具箱进行求解，解决了在应力及强度服从对数正态分布的情况下，蜗杆传动的可靠性优化设计的问题；由表1及表2得出的结果来看，MATLAB优化工具箱不仅算法可靠，而且编程简单，使设计效率也有很大提高。

(2)与常规的设计方法相比较，可靠性优化设计的效益十分可观。首先蜗杆传动副的整体体积得到了很大减少；其次，按常规设计所得到的蜗杆传动的可靠度在使用10年后仍能达到0.951066，这很显然造成了材料的浪费。而按本文的设计方法所得到的蜗杆传动的可靠度在8年内均能达到所要求的可靠度0.99，刚好满足设计使用期限，实现零部件的合理利用。

[1] 刘混举. 机械可靠性设计[M]. 北京：科学出版社，2012.

[2] 贺向东，张义民，薛玉春，等. 压杆稳定可靠性优化设计[J]. 中国工程科学，2007，9(5)：33-35.

[3] 张义民. 机械可靠性设计的内涵与递进[J]. 机械工程学报，2010，46(14)：167-188.

[4] 魏宗平，李飞舟. 机床主轴结构非概率可靠性优化设计[J]. 组合机床与自动化加工技术，2009(12)：17-20.

[5] 樊立梅. 基于MATLAB的斜齿轮传动多目标可靠性优化设计[J]. 机械设计与制造，2008，8(8)：15-16.

[6] Tae Min Cho, Byung Chai Lee．Reliability-based design optimization using a family of methods of moving asymptotes [J]．Structural and Multidisciplinary Optimization，2010，42(2)：255-268．

[7] 张伟强，佟连福. 蜗杆传动的可靠性设计[J]. 科技资讯，2008，1(3)：28.

[8] 王启，王文博. 常用机械零部件可靠性设计[M]. 北京：机械工业出版社，1996.

[9] 濮良贵，纪名刚. 机械设计(第八版)[M]. 北京：高等教育出版社，2006.

[10] 龚纯，王正林. 精通MATLAB最优化计算(第二版)[M]. 北京：电子工业出版社，2012.

(编辑 李秀敏)

Research on Reliability Optimization Design of Worm-Drive

HU Qi-guo，XIE Guo-bin，TUO Kui

(College of Mechatronics and Automotive Engineering , Chongqing Jiaotong University , Chongqing 400074 , China)

Based on the integration of reliability design theory and optimization design theory, the reliability optimization design of the worm-drive is extensively discussed when its stress and intensity obey logarithmic normal distribution, and the mathematic model of reliability optimization design of the worm-drive is built. It obtains the reliable and optimal parameter by using the Matlab optimization toolbox, and demonstrates the feasibility of this method in the reliability of worm-drive. The optimal results show that this method not only improves the efficiency and reliability of the worm-drive design, but also can be of significance reference value in solving optimal design issue of the other mechanisms.

worm-drive；optimization toolbox of Matlab；reliability

1001-2265(2014)07-0042-03

10.13462/j.cnki.mmtamt.2014.07.012

2013-10-19

胡启国(1968—)，男，重庆人，重庆交通大学教授，博士，主要从事机械可靠性及机械系统动力学的教学与研究，(E-mail)swpihqg@126.com；通讯作者:谢国宾(1988—)，男，河南扶沟人，重庆交通大学硕士研究生，主要从事机械可靠性及机械系统动力学的研究，(E-mail)xgbin008vip@126.com。

TH122;TG65

A