基于瑞利法的压电微夹持器动力学建模与优化*
2014-07-18李龙根陈永刚
李龙根,陈永刚,2
(1.东莞职业技术学院 机电工程系,广东 东莞 523808;2. 广东工业大学 机械工程学院,广州 510006)
基于瑞利法的压电微夹持器动力学建模与优化*
李龙根1,陈永刚1,2
(1.东莞职业技术学院 机电工程系,广东 东莞 523808;2. 广东工业大学 机械工程学院,广州 510006)
压电微夹持器优越的动力学性能对引线键合设备高效工作和延长使用寿命具有重要意义。文章利用瑞利法对压电微夹持器进行动力学建模,并将结果与其他求解结果进行对比,证明了瑞利法求解结果更接近精确解。在搭建动力学模型基础上采用遗传算法进行优化,得到动力学结构最优配置。研究结果为更深入开展压电微夹持器动力学分析提供了一定的支持。
瑞利法;压电微夹持器;动力学模型;遗传算法;优化
0 引言
引线键合是LED芯片制造的重要环节,其基本原理是通过超声、压力与温度等多能场能量的耦合,实现芯片(Die)与引线框架(Lead frame)之间的互连。目前,引线键合装备正向更高产能、功能性更强、系统更稳定等方向发展[1]。压电微夹持器是引线键合系统关键部件之一,它的基本作用是,利用自身机构夹紧与张开运动,对数十微米引线进行固定与放松的操作,通过与其它机构协同工作,实现引线键合功能。压电微夹持器广泛应用在医学微动平台、机器人焊接、太空探索中的太空材料提取等方面[2-5]。压电微夹持器在高速张开和闭合中,需要提高自身固有频率以避开系统频率,避免张开与关闭的振动,当弹性元件质量远远小于振动物体的集中质量时可略而不计,原来有分布质量的振动系统可简化为简单的自由度振动系统。然而,该抽象模型的振动系统中弹性元件的分布质量并不小于集中质量,对于这样的振动系统,可以利用瑞利法把能量加以引申,考虑分布质量的影响[6],搭建其动力学模型并进行优化,得到压电微夹持器的最高固有频率,从而有效避免与系统发生共振。这对于引线键合系统高效工作和使用寿命具有重要意义。
1 压电驱动微夹持器
1.1 系统组成
引线微夹持器综合利用了柔性联接与压电智能材料组合的概念[6-9]。本文引线微夹持器包括:压电陶瓷堆、直臂、红宝石等,如图1所示。通过电信号驱动,压电陶瓷经逆压电效应产生位移运动,通过柔性铰链带动系统支臂打开,即将引线放开;当压电陶瓷材料不加载电信号,系统回到初始位置,即对引线夹持与固定。在持续电信号驱动下,微夹持器将对引线进行固定与放松的连续操作,以实现焊线的键合工艺要求。
1.2 微夹持器模型
由于该微夹持器是对称结构,所以取其下部进行动力学分析。因为压电陶瓷堆把振动动力传递给柔性连接,柔性连接再作用支臂实现微夹持器的夹紧和松开功能。我们在这里把柔性连接部分和支臂部分组成的系统进行抽象建模得到悬臂梁的模型;由于红宝石具有一定的质量,抽象为悬臂梁一端的一个质量块为m,如图2所示。

图1 IC/LED引线微夹持器原理图
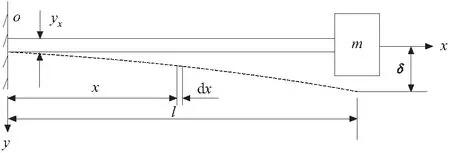
图2 抽象模型
2 动力学模型搭建
利用瑞利法对建立的抽象模型进行动力学建模,求出系统的基频,这样在系统加载振动动力的时候就可以避开共振,降低对于微夹持器的破坏,延长了使用寿命。
将微夹持器对称结构的下半部分简化为如图2所示的模型,取简化后悬臂梁单位长度质量为ρ,梁端点有集中质量为m,弹性模量为E,惯性矩为I=bh3/12,长度为l,由材料力学可知,在梁端静载荷F的作用下,悬臂梁在截面x处的挠度为:
(1)
而梁的振动可表示为
y(x)=y(x)sinωnt
(2)
其中,ωn是圆频率,t是时间。
则梁动能的最大值为:
(3)
故整个系统的动能的最大值为:
(4)
而系统的势能的最大值为:
(5)
此系统为保守系统,则:
Tmax=Vmax
(6)
所以:
(7)
则,
(8)

(9)
将梁的均布质量向自由端简化,则可假定梁在横向振动时变形曲线的形式同梁在自由端有一静载荷作用下产生的静弯曲线相同,当m=0时:
(10)
假定梁在横向振动时弯曲曲线y(x)的形式与在均布载荷作用下产生的静变形曲线相同,则系统的固有频率为[6]:
(11)
用瑞利法求得系统的固有频率都与精确解的误差为0.4%,而质量为0时求得固有频率与精确解误差约为1.5%,如图3所示。瑞利法搭建动力学模型求解系统固有频率与精确解更接近。
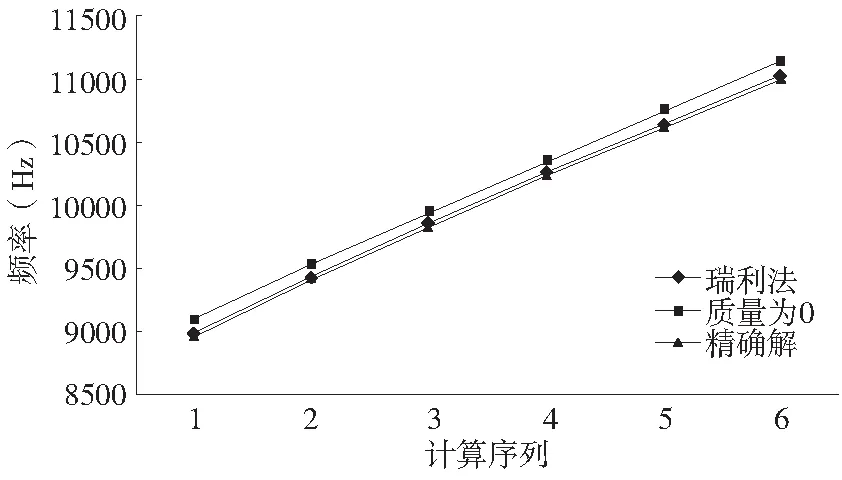
图3 瑞利法与其他方法比较
3 优化
通过对微夹持器进行优化,得到其更高的固有频率,这对于避免与其他部件产生共振和保障自身刚度及其使用寿命具有重要意义。遗传算法效仿生物界“物竞天择,适者生存”的演化法则,把问题参数编码为染色体,再利用迭代方式进行选择、交叉及变异等运算来交换种群中染色体信息,以最终实现符合优化目标的染色体[10]。遗传算法以不依赖问题的具体领域和对问题种类有很强的鲁棒性的优势广泛应用与各种科学领域,它提供了一种复杂系统优化问题的通用求解框架。利用遗传算法计算通过瑞利法搭建固有频率目标函数的最大值,选择二进制编码,遗传算法相关参数设置如表1所示。

表1 遗传算法相关参数
图4所示为目标函数图,其中“o”是每一代的最优解。从图中可知,最优解大部分集中在图形顶端,即最大固有频率位置。图5所示为种群优化50代的进化图,在进化过程中,目标解在迭代到12次时就进入了收敛,这也体现了利用遗传算法的快速收敛的优点。通过优化得到最优解:b=h=0.49993 mm,最大固有频率为205.3219 Hz。

图4 瑞利法三维模型及每代最优解

图5 基于瑞利法模型最优解进行过程
4 总结
本文对LED引线键合中压电微夹持器建立抽象模型,运用瑞利法对其模型进行建模分析,得到了微夹持器的固有频率,并将结果与其他求解结果进行对比,瑞利法求解结果与精确解的误差为0.4%。在搭建动力学模型基础上采用遗传算法进行优化,通过优化得到最优解:b=h=0.49993 mm,最大固有频率为205.3219 Hz。这为微夹持器的动载荷加载时避免与固有频率相近产生共振现象,延长了压电微夹持器的使用寿命,对于压电微夹持器的发展起到了一定的推动作用。
[1] Zhili Long, Lufan Zhang, Jianguo Zhang. FEM Design and Experiment of a Micro-Gripper Based on Piezoelectric Material[C]. Advanced Materials Research, Switzerland: Trans Tech Publications, 2012, 434-438.
[2] Rao R., Tummala. Microelectronics Packing Handbook [M]. Holland: Kluwer Academic Publisher. 2001.
[3] G.G. Harman. Wire Bonding in Microelectronics: Materials, Processes Reliability and Yield, 2nd Edition[M]. New York: McGraw-Hill, 1997.
[4] 张福学.现代压电学下[M]. 北京:科学出版社, 2002.
[5] 应崇福.超声学[M], 北京:科学出版社, 1990.
[6] 王伟.振动力学与工程应用[M]. 郑州:郑州大学出版社,2008.
[7] Shorya Awtar,Alexander H. Slocum .Constraint-Based Design of Parallel Kinematic XY Flexure Mechanisms[J].Journal of Mechanical Design, 2007,129(8): 816-830.
[8] 于靖军,裴旭,毕树生,等.柔性铰链机构设计方法的研究进展[J]. 机械工程学报,2010,46(13):2-13.
[9] 阴学朴.平行梁结构电热微夹持器研究[D]. 秦皇岛:燕山大学,2007.
[10]史峰,王辉,郁磊,等,MATLAB智能算法30个案例分析[M]. 北京:北京航空航天大学出版社,2011.
(编辑 李秀敏)
Dynamical Modeling and Optimization of Piezoelectric Micro Gripper Based on Rayleigh′s Method
LI Long-gen1,CHEN Yong-gang1,2
(1.Department of Mechanical and Electrical Engineering Dongguan Polytechnic, dongguan Guangdong 523808, China;2.College of Mechanical and Electrical Engineering Guangdong University of Technology, Guangzhou 510006, China)
It is an important significance for high efficient working and service life extension of wire bonding equipment to have superior dynamic performance of piezoelectric micro gripper. The dynamical model of is built by Rayleigh’s Method, and its result is compared with others, the result of Rayleigh’s Method is more close to the exact solution. The dynamical model is optimized by genetic algorithm (GA) and optimal configurations are obtained. The results provide a certain support to carry out dynamical analysis of piezoelectric micro gripper in a deep-going way.
rayleigh’s method; piezoelectric micro gripper; dynamical model; GA; optimization
1001-2265(2014)07-0009-03
10.13462/j.cnki.mmtamt.2014.07.003
2013-12-02
国家自然科学基金(51305082)
李龙根(1966—),男,江西吉安人,东莞职业技术学院副教授,硕士,研究方向为机械制造,(E-mail)mslilg@163.com。
TH166;TG65
A
