碗形砂轮热力结构耦合作用对磨削可转位刀片的精度影响*

张祥雷，姚 斌,2，王萌萌，陈 站，朱 健

(1.厦门大学 物理与机电工程学院，福建 厦门 361005；2.陕西理工学院 机械工程学院，陕西 汉中723003)

碗形砂轮热力结构耦合作用对磨削可转位刀片的精度影响*

张祥雷1，姚 斌1,2，王萌萌1，陈 站1，朱 健1

(1.厦门大学 物理与机电工程学院，福建 厦门 361005；2.陕西理工学院 机械工程学院，陕西 汉中723003)

针对可转位刀片周边刃磨的五轴数控工具磨床，研究其高速旋转碗型砂轮的热力结构耦合特性，得到砂轮尺寸变化对磨削刀片的精度影响。首先考虑高速旋转的砂轮受离心力的作用导致外形尺寸的变化，并进一步研究其在不同的转速下应力刚化与旋转软化对其尺寸精度的影响。同时，采用磨削运动的三角形热源理论模型，计算相关热量与温度，并进行仿真，获得砂轮磨削40s的温度变化情况以及温度场云图。最后综合考虑砂轮受离心力、磨削热共同作用下的热-力-结构耦合情况在不同转速下的结构变形。相关的分析结果为砂轮在磨削可转位刀片过程中的刀片精度控制与补偿具有一定的参考价值。

工具磨床;砂轮;离心力;磨削热

0 引言

硬质合金可转位刀片因为具有不需重磨、可迅速转位、更换切削刃的辅助时间短、重复定位精度高、能够提高劳动生产率等特点，在高效、精密数控加工中的应用日趋广泛。图1所示为专门用于加工硬质合金可转位刀片的CNC可转位刀片周边五轴工具磨床磨削部分结构简图,其有XYABC五个运动轴联动机床形式(包括砂轮主轴箱所在的X、Y两个移动轴和夹具所在的A、B、C三个旋转轴)。图2所示为此工具磨床加工刀片用的碗型砂轮。

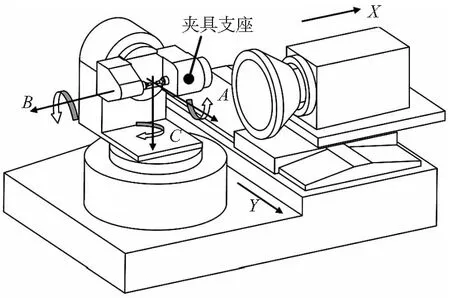
图1 可转位刀片周边五轴工具磨床磨削部分简图

图2 金刚石砂轮

在精密磨削加工中，由磨削力、热变形所引起的制造误差占总制造误差的40%～70%[1]。针对磨削力、磨削温度场对制造精度影响的研究，众多学者做了大量的工作[2-3],但是针对高速旋转砂轮受离心力引起的制造精度问题，还很少有研究文献见诸，常见考虑离心力的研究主要集中主轴单元[4]、轮盘[5]、涡轮叶片[6]等。在高速、精密数控磨削加工中，高速旋转的砂轮外形变化势必对刀片的磨削精度产生一定的影响，为了提高磨削精度，建立了碗型砂轮的有限元模型，综合分析其在不同的磨削转速下受应力刚化、旋转软化和磨削热共同作用时砂轮变形情况，进而探讨砂轮热力耦合变形对制造精度的影响。

1 应力刚化与旋转软化分析

碗型砂轮结构是轴对称的，沿着砂轮轴向可将碗型砂轮看做由若干个变半径变厚度的空心圆盘连接而成，它们旋转时会在离心力作用下发生膨胀变形。砂轮的端截面为空心旋转圆盘，如图3所示，设圆盘内孔表面与外边界均无面力，则砂轮的端截面应变分量为[9]：

图3 砂轮端截面的示意图

(1)

(2)

其中，a、b为砂轮端截面的内外半径，r为半径，ν为泊松比，ρ为密度，ω为角速度，E为弹性模量。

设砂轮沿轴向坐标为x，则径向变形可以表达为：

u(x)=

(3)

当砂轮在高速旋转时，由于离心力对砂轮运动产生预应力的影响，导致砂轮刚度发生改变。与此同时，由于离心力作用使砂轮发生不同程度的变形，这种变形引起刚度减小称为旋转软化[10]。因此，砂轮转速的变化不但产生不同的离心力，也会使砂轮发生应力刚化和旋转软化的作用，从而使砂轮基体的刚度和应力发生变化，下面将对其进行有限元仿真分析。

将碗型砂轮建立三维有限元模型，碗型砂轮基体材料为40Cr，弹性模量EX=2.1e11 N/m2，泊松比σ=0.28，密度ρ=7870kg/m3，砂轮端面最大直径为400mm，砂轮的厚度为250mm，采用SOLID95三维实体单元对结构进行扫略网格划分，在砂轮安装部位接触的面上施加约束，并施加全局角速度载荷，砂轮最大线速度是120m/s。仿真砂轮在不同转速下受离心力作用产生的最大几何尺寸变形和最大应力的变化数据如图4所示，其中横坐标是转速(r/min)。考虑砂轮受应力刚化和旋转软化的作用，砂轮最大几何尺寸变形和应力的结果数据如图5所示。由结果图可知，砂轮的最大位移变形与最大应力值随着转速的增加而增加，呈非线性上升趋势，同样应力刚化与旋转软化的影响也随转速提高呈非线性增加，且增幅非常大。因此，为了精密磨削可转位刀片，在数控刀位计算中，针对砂轮尺寸变化所引起的直径和宽度变化要加以补偿，补偿值可参照图5的数据。当然，图1数据仅可作定性的参考，具体变化值仍需结合实际中的测量情况。

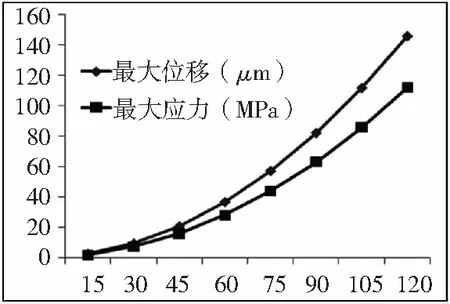
图4 砂轮最大位移、应力值

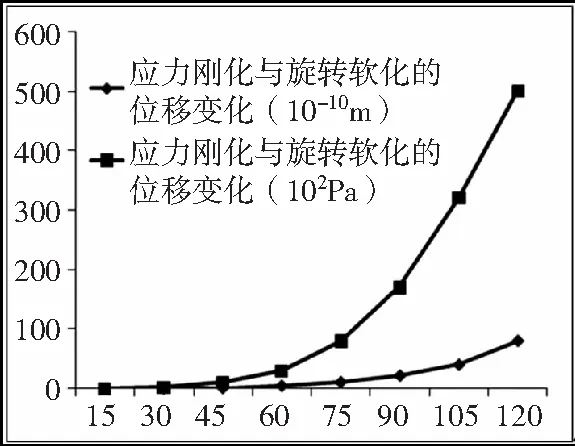
图5 考虑应力刚化与旋转软化的砂轮位移、应力变化值

2 砂轮磨削热的计算与仿真

磨削温度是加工时由磨削热所引起的工件温度升高的总称，主要是由摩擦和切削变形产生的[11-12]。磨削过程就其实质而言是一种由大量无规则的离散分布在砂轮表面的磨粒所完成的滑擦、耕犁、切削作用的随机综合。实际磨削可转位刀片采用一次性磨削，故切削深度较大，接触弧长也较长，从磨削区的切削和摩擦情况来看，磨粒上所受的力，由切入处向切出处逐渐变大，故采用三角形热源分布更为合理。根据J.C.Jaeger提出的磨削运动热源的理论模型，假设磨削区域热通量为q，并以速度v移动产生的温度场T公式为[13]：

(4)

其中，K0是零阶二类Bessel函数，λ是导热率，a=λ/(ρc)是热扩散率，ρ是材料密度，c是比热容，积分变量li代表了热源的位置。将初始条件z=0 代入可得

(5)

当x=-lc/2时，即接近热源的移出端时，T(x，0)温度值最大，此时：

(6)

关于热量q的求法，许多学者都做了专门的研究，提出了许多不同的方法与模型，此处采用 Outwater 和 Shaw 的方法，他们认为热量q可以通过磨削力求得，磨削过程中的机械能转换为热能[8]：

QT=Ft(Vs+Vw)

(7)

其中，Ft为切向磨削力，Vs为磨削进给速度，Vw为热源移动速度，由于热源移动速度远大于进给速度，式(7)中进给速度可以忽略不计。

q=βQT/A

(8)

其中，β为传入工件的热量比，可根据C.Guo和S.Malkin的热分配比模型计算；A为磨削接触区面积。

超高速磨削过程中达到最高磨削温度的时间是很短的，一般仅有百分之几秒，这是因为工件速度较高，即热源运动速度较高。在此考虑了冷却液、空气介质对流换热的情况，把模型建成三维的且有X、Y、Z三个方向，有移动热源的磨削温度场满足瞬时温度场模型，即[15]：

(9)

磨削温度场没有内热源，则最后一项为零。在磨削温度的有限元仿真过程中，由于实际边界条件复杂，故此需要对边界问题进行了必要的简化。磨削的工件为硬质合金可转位刀片，砂轮线速度为120m/s。由于碗型砂轮磨削可转位刀片属于高速端面磨削，磨削区域温度迅速在砂轮端面扩展，故将热源进行简化，直接在砂轮的端面施加面载荷热流密度，同时在砂轮的表面施加对流换热系数，以模拟冷却液和空气所带走的热量。砂轮40s瞬态热分析仿真结果如图6所示，图7为砂轮端面某节点的温升曲线，图8为其热变形云图。

图6 砂轮磨削40s后的瞬态温度云图

图7 砂轮端面磨削40s的温升曲线图

图8 砂轮磨削40s后的热变形云图

3 高速旋转砂轮热力结构耦合分析

在以上分析基础上，综合考虑转速、离心力、磨削热对砂轮温度场分布情况的影响以及砂轮热力结构耦合变形，通过热弹性本构方程，建立热力耦合方程，应用变分原理，产生下列有限元矩阵方程[15]：

(10)

高速砂轮热力结构耦合分析采用顺序耦合的方式，温度场分析采用了SOLID90单元，热变形分析转换为结构单元SOLID186，并假设初始温度为20℃，砂轮磨削时间40s。分析高速砂轮在最高转速范围内因离心力、磨削热的作用产生的变形和热应力，结果如图8所示。其中横坐标单位为m/s。

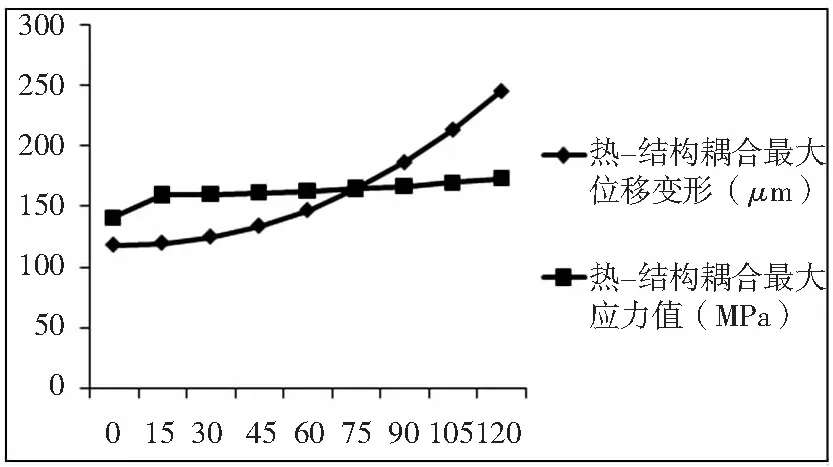
图9 砂轮热-结构耦合分析结果

由图9可知，随着转速的增加，砂轮的位移变形与应力值都呈非线性增加，但应力的增加呈减缓趋势，说明温升可减少应力集中。碗型砂轮的尺寸位移变形势必影响可转位刀片的加工精度，比如砂轮沿轴向后扩，刀片的磨削量就会减少，这必然影响磨削精度。

4 总结

五轴数控工具磨床的碗型砂轮在不同的转速下会因离心力作用而产生不同的尺寸变化，通过力学分析、有限仿真、理论计算和所得分析数据，系统地剖析了在高速旋转下的砂轮外形变化对刀片的磨削精度所产生的一定影响。其中着重分析了应力刚化、旋转软化随转速的变化对砂轮尺寸的影响，磨削热对砂轮基体的热变形，并综合分析了它们对碗型砂轮外形轮廓的作用。为了提高可转位刀片的磨削精度和消除砂轮尺寸变形影响，有必要针对砂轮尺寸变化所引起的直径和宽度变化加以补偿，以上的研究为提高刀片磨削精度和消除此影响提供了理论依据。

[1] 姚博世, 谭晓庆, 贺文辉. 砂轮离心力对磨削精度的影响[J]. 机电技术, 2011(10): 36-38.

[2] 明兴祖, 严宏志, 陈书涵, 等. 3D力热耦合磨齿模型与数值分析[J]. 机械工程学报, 2008, 44(5): 17-24.

[3] 黄志刚, 柯映林, 王立涛. 金属切削加工的热力耦合模型及有限元模拟研究[J]. 航空学报, 2004, 25(3): 317-320.

[4] 曹宏瑞, 李兵, 陈雪峰, 等. 高速主轴离心膨胀及对轴承动态特性的影响[J]. 机械工程学报, 2012, 48(19): 59-64.

[5] 宋兆泓, 熊昌炳, 郑光华. 航空燃气涡轮发动机强度设计[M]. 北京:北京航空学院出版社, 1988.

[6] 郭军刚, 韩志富, 胡丽国, 等. 涡轮叶片材料非线性应力数值分析[J]. 导弹与航天运载技术, 2007(6): 40-44.

[7] 王媛媛, 姚斌, 张德云, 等. 多线型组合平面刀具的自动编程磨削技术[J], 工具技术，2010, 44(3): 48-50.

[8] 刘立明, 侯忠滨, 王友利. 基于UG 的可转位刀具参数化设计[J]. 工具技术. 2007, 41(6): 65-67.

[9] 徐秉业, 刘信声. 应用弹塑性力学[M]. 北京：清华大学出版社, 1995.

[10] 杨永谦, 肖金生. 实用有限元分析技术——ANSYS专题与技巧[M]. 北京：机械工业出版社, 2010.

[11] 谢桂芝, 黄含, 盛晓敏，等. 工程陶瓷高效深磨磨削力和损伤的研究[J]. 湖南大学学报(自然科学版), 2008, 35(5): 26-30.

[12] G.Z.Xie, H.huang. An experimental investigation of temperature in high speed deep grinding of partially stabilized zirconia[J]. International journal of Machine tools & Manufacture, 2008, 48: 1562-1568.

[13] 盛晓敏, 宓海青, 谢桂芝，等. 超高速磨削技术[M]. 北京：机械工业出版社, 2010.

[14] Outwater J O, Shaw M C. Surface temperatures in grinding[J]. Trans ASME. 1952, 74: 73-78.

[15] 张朝晖. ANSYS12.0热分析工程实战手册[M]. 北京：中国铁道出版社, 2010.

[16] 陈虹微, 王荣杰. 基于模型的离心压缩机电机振动应用研究[J]. 徐州工程学院学报(自然科学版), 2012, 27(4): 69-73.

(编辑 李秀敏)

The Effect of Thermal-Mechanical-Structure Coupling on Precision for Indexable Insert Grinded by Bowl Wheel

ZHANG Xiang-lei1, YAO Bin1,2, WANG Meng-meng1, CHEN Zhan1, ZHU Jian1

(1.Department of Mechanical and Electrical Engineering, Xiamen University, Xiamen Fujian 361005, China; 2. School of Mechanical Engineering，Shaanxi University of Technology, Hanzhong Shanxi 723003, China)

For the five-axis CNC tool grinder of grinding indexable insert around, the paper studied thermal-force-structure coupling characteristics of its high-speed rotating bowl grinding wheel, and obtained how the grinding wheel size variation affected the accuracy of the blade. Firstly, considering the effect of centrifugal force on the high-speed rotating wheel by which leads to overall dimensions change, the paper further studied stress stiffening and spin softening effect on the dimensional accuracy under different rotational speed. Meanwhile, the paper used the grinding movement triangular heat source model to calculate the heat and temperature and carried out the simulation of grinding, which obtained the grinding temperature variation and the temperature field cloud picture of 40 seconds. Finally, comprehensively considering the structural deformation under centrifugal force and grinding heat couple action in different speeds, related analysis results have a certain reference value on the blade precision control and compensation for grinding indexable insert.

tool grinder; wheel; centrifugal force; grinding temperature

1001-2265(2014)07-0015-04

10.13462/j.cnki.mmtamt.2014.07.005

2013-10-07；

2013-10-28

数控国家科技重大专项(2010ZX04001-162)

张祥雷(1987—)，男，浙江温州人，厦门大学博士研究生，主要研究方向是多轴数控加工、机械结构设计与优化及有限元分析等，(E-mail)zhxile2008@sina.com。

TH166;TG593

A