时域与频域两点法误差分离技术的精度分析*
2014-07-18母德强谢新旺
母德强,崔 博,谢新旺,陈 懿
(长春工业大学 机电工程学院,长春 130012)
时域与频域两点法误差分离技术的精度分析*
母德强,崔 博,谢新旺,陈 懿
(长春工业大学 机电工程学院,长春 130012)
为了分析时域与频域两点法误差分离技术中所包含的原理误差及该原理误差的规律和特性,建立了进行误差分离的零件模型,通过对不同影响因素的分析找到了两点法误差分离技术所含原理误差的规律和特性,并对两种误差分离技术的精度进行了比较。使用时域与频域两种误差分离技术和圆度测量仪对同一零件进行测量比对,发现仿真结果和实验结果与理论分析相符。因此得出结论:采样点数N每扩大一倍,各参数的绝对误差值的比值越来越接近于2;对置安装传感器使两点法分离结果的误差最小;在相同的采样参数下,频域法误差分离技术的分离精度高于时域法。
两点法;误差分离;原理误差;影响因素;影响规律
0 引言
近年来,随着高精度机械加工技术的不断发展,对零件形位误差也在不断地提高。为了保证被加工工件的形位精度要求,在线测量是首选的检测方法。而由于加工系统中存在着许多不可预测的影响因素,使得对工件形位误差的在线测量变得十分困难,误差分离技术(Error separation technique,EST)的出现为形位误差的在线测量提供了可能[1]。
在众多的误差分离技术中,两点法误差分离技术因容易安装而受到许多研究者的青睐。两点法误差分离技术也可以分为时域两点法误差分离技术和频域两点法误差分离技术,但无论是时域两点法还是频域两点法,他们都存在缺陷:因原理误差的存在,使该方法无法完全分离零件的偏心误差。此外两点法误差分离技术的分离结果的误差规律还没有一个明确的规则。本文正是基于此而进行的探索,分别对时域两点法和频域两点法原理误差的影响因素及影响规律进行了研究,并比较两种方法的分离精度,力求提高两点法误差分离技术在线测量的精度。
1 两点法误差分离原理
两点法误差分离技术是从三点法误差分离技术发展而来的。三点法误差分离原理如图1所示。
O为传感器A、B和C所在位置处的位移敏感中心线的交点。在以O为原点,A、B的中心线分别取为X轴和Y轴的测量坐标系中,O0为截面的最小二乘心,与实际回转中心O的偏心距为e[2]。

图1 三点法误差分离原理图
设工件的圆度误差为h(θ);主轴回转误差在x,y上的分量分别为δx(θ)和δy(θ);传感器之间的夹角如图1所示[2]。则三个传感器的输出为
sA(θ)=h(θ)+δx(θ)
(1)
sB(θ)=h(θ+α)+δx(θ)cos(α)+δy(θ)sin(α)
(2)
sC(θ)=h(θ+α+β)+δx(θ)cos(α+β)+δy(θ)sin(α+β)
(3)
对(1)~(3)式乘以不等权系数1,a和b,然后相加得到三点法误差分离的基本方程
s(θ)=sA(θ)+asB(θ)+bsC(θ)
=h(θ)+ah(θ+α)+bh(θ+α+β)
(4)


式中m、p为整数,将(4)式离散化,得
s(n)=h(n)+ah(n+m)+bh(n+m+p)
=sA(n)+asB(n)+bsC(n)
(5)
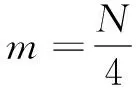
因此等式(5)可以化为
s(n)≈h(n)+bh(n+m+p)
=sA(n)+bsC(n)
(6)
1.1 频域两点法误差分离技术原理
sA(n) 、sC(n)都为所测得的已知量。对式(6)作离散傅立叶变换,根据傅立叶变换的时延相移特性可得
S(k)=H(k)G(k)
(7)
在式(7)中:S(k)=DFT[s(n)];H(k)=DFT[h(n)];G(k)=1+bej2π(m+p)k/N。
由h(n)=DFT-1[H(k)]=DFT-1[S(k)/G(k)],可求出工件的圆度误差h(θ)的离散形式h(n)。
使用频域法进行求解时,若被测工件表面存在突变点而不连续,傅立叶变换会使变换结果产生严重的失真,从而影响计算精度[3]。因此洪迈生[2]等人提出了时域两点法误差分离技术。
1.2 时域两点法误差分离技术原理
当α+β→180°,a→0,b→1 。式(5)因而变为
s(n)≈h(n)+bh(n+m+p) =sA(n)+bsC(n)
(8)
令l=m+p,将(8)改写为

(9)

2 影响两点法的因素及其规律分析
误差分离技术在分离的过程中会受到很多因素的干扰,如:采样误差、谐波抑制、传感器安装误差、噪声及其随即干扰等[4]。
噪声可以经降噪滤波减小甚至消除其影响;随即干扰是无法避免的,只能通过多组求平均值来尽可能的减小。因此影响时域法误差分离技术的因素主要有谐波抑制、采样误差和传感器安装误差。
2.1 谐波抑制对两点法的影响
谐波抑制现象只出现在傅立叶变换的过程中,因此谐波抑制只对频域法误差分离技术有影响。在三点法误差分离技术中应用傅立叶逆变换时,不论参数m、p、α、β如何取值,都有G(1)≡0,常用的处理方法是令S(1)=0。在傅立叶逆变换时,该位置的谐波分量就因为置零而损失[5],从而引入谐波抑制现象。为了避免谐波抑制,令G(1)=1[4]。然后在进行傅氏逆变换就可以得到被测工件的圆度误差h(θ)的离散形式h(n)。
但是,在频域两点法误差分离技术中。
G(k)=1+bej2π(m+p)k/N
(10)
所以G(k)≠0,k∈(0,N-1)恒成立。所以两点法误差分离技术中不存在谐波抑制现象。
2.2 采样点数对两点法的影响
传感器B所采集序列在进行消除回转误差时的常权系数a=-sin(α+β)/sinβ。当N增大时会使得α+β→180°,因而a→0;但a不等于零。在其他条件都正确的条件下,忽略传感器B就无法完全消除主轴回转运动误差。设aN、αN、βN、γN为采样点数取N时参数a、α、β、γ的值,所以采样点数对误差的影响取决于
f(N)=aN[δx(θ)cosαN+δy(θ)sinαN]
(11)
的大小。则
(12)
因γN=2π/N,所以采样点数N越大,角度γN越小,tan2γN越趋近于0。则
(13)
通过以上分析可知:应用频域法和时域法时,采样点数N越大,分离结果的绝对误差值越小;aN/a2N→2,说明各参数的绝对误差值随着采样点数N的增大而减小的倍数越来越趋近于2。
2.3 安装角度对两点法的影响
因为γN=2π/N,当采样点数N过大,会使夹角γN过小。从而给传感器C的安装带来困难。当传感器C的安装角度不精确时,也会给分离结果带来误差。
在安装传感器C的时候,设角度α+β的安装角度误差为Δφ,则
s(θ)≈sA(θ)+bsC(θ+Δφ)
=h(θ)+δx(θ)+bh(θ+α+β+Δφ)
+bδx(θ)cos(α+β+Δφ)+bδy(θ)sin(α+β+Δφ)
(14)
又δx(θ)=e0cosθ、δy(θ)=e0sinθ、α+β=π-γ,则
s(θ)≈s′(θ)=h(θ)+bh(θ+α+β+Δφ)
+e0cosθ-be0cos(θ+γ-Δφ)
(15)
由式(15)可看出,由偏心误差和安装角度误差共同引起的误差大小为
g(Δφ)=e0cosθ-be0cos(θ+γ-Δφ)
(16)
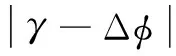
因此对置安装两个传感器对频域法和时域法误差分离技术来说,有利于消除转轴的偏心误差。
3 仿真分析
为了检验上述的分析并比较两种方法的精度,我们进行了如下的仿真验证。
3.1 采样点数对两点法误差分离技术的影响
在仿真实验中,取基本半径为20mm、偏心距为3mm、表面有四组振幅为3mm的正弦波所叠加而成的轴。保证除采样点数N除外的一切条件不变,N的取值为16、32、64、128、256、512、1024、2048。采集这几组信号,分别用时域法与频域法对数据进行分析,结果如表1所示。

表1 时域两点法与频域两点法的分离结果比较
通过表1可以看出:各量的绝对误差值随着采样点数N的增大而减小,且减小的倍数越来越接近于2;当采样点数N≥256时,可认为圆度误差值的绝对误差减小的倍数等于2;在相同的采样点数下,频域法中的绝对误差要明显小于时域法,因此频域法精度要高于时域法。证明了采样点数对误差值的影响规律的理论分析是正确的。
3.2 安装角度对两点法误差分离技术的影响
在检测安装角度对分离误差带来的影响时,选取的采样点数N=256,所以α+β的理论角度应为178.59375°。令安装角度α+β的值从174.6°到180.6°等间隔变化,间隔为0.2°,除此之外保证其他参数不变。
检验时把数据分别做时域和频域分析。分析时的数据为:被测件基本半径为20mm,表面上有振幅为3mm的正弦信号。偏心距取3mm。结果如图2所示。
由图2知:时域法中,分离误差会随着安装角度的增大而减小,在180°的位置达到极值并大致关于180°对称。频域法中,分离误差会随着安装角度的增大而减小,在180°的位置达到极值并且关于180°对称。对置安装使两种方法的分离精度都得到提高。证明了3.3中的分析和推导是正确的。
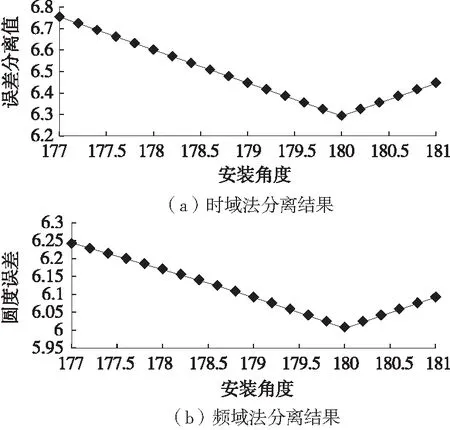
图2 安装角度对两点法误差分离技术的影响
4 试验验证
通过上面的仿真分析验证了影响两点法误差的因素及其影响规律符合理论分析。在实验室环境内通过实验来进一步验证理论分析与仿真分析。
实验所用设备为:通过磨削加工一个长度280mm,直径为50mm的轴进行验证;传感器采用的是德国米铱的NCDT系统控制的单通道精密电容位移传感器CapaNCDT620[6-8]。实验时,分别取采样点数N=64、128、256、512,则安装角度α+β=(1-2/N)π。对工件测量5遍取平均值以减小测量过程中的随机误差。结果如表2所示:

表2 实验验证误差分离结果 (单位:μm)
通过试验结果可看出:两种分离方法的分离结果与理论分析和仿真验证相符,证明了在使用两点法误差分离技术时,对置安装两传感器可以得到更高的精度,且频域法的精度要高于时域法。
5 结论
(1)相同的检测条件下,频域法比时域法具有更高的分离精度;
(2)实际的加工过程中,检测时采用对置安装传感器可以得到更精确的圆度误差值;
(3)在时域法和频域法中,采样点数N越大,有aN/a2N→2,从而说明采样点数N每扩大一倍,各参数的绝对误差值的比值越来越接近于2;
(4)两点法误差分离技术虽然有原理误差,但选择合适的参数后仍可达到很高的精度;因此,在一定精度要求下仍然可以使用。
[1] 张镭,赵莹,张玉. 三测头法误差分离技术的理论与试验[J]. 机械工程学报,2009,45(6):256-261.
[2] 洪迈生,邓宗煌.圆度和回转运动误差的时域二点法分离技术[J].中国机械工程,1997,8(2):88-89,92.
[3] 张玉梅.基于多尺度分析的圆度误差在线检测研究[D].长春:吉林大学,2009.
[4] 黄建健.基于频域三点法的主轴回转误差的测量方法与应用研究[D].广州:广东工业大学,2011.
[5] 李超. 基于误差分离技术的精密回转及直线运动部件精度测量[D].哈尔滨:哈尔滨工业大学,2010.
[6] Horikawa O, Maruyama N. A low cost high accuracy round-ness measuring system [J]. Precision Engineering,2001,25(4):254-259.
[7] Kim K, Lee S, Jung H B. Assessing roundness errors using discretevoronoi diagrams [M]. [S.I.]:Advanced Manufacturing Technology,2000.
[8] 曹麟祥,王丙甲.圆度检测技术[M].北京:国防工业出版社,1998.
[9] 丁曙光,李浩,桂贵生. 三点法圆度误差分离技术在轴类零件测量中的应用研究[J].机床与液压,2008,36(2):116-118.
[10]雷贤卿,李言,周彦伟,等.3点法圆度误差分离技术的新算法 [J].兵工学报,2007,28(1):73-77.
[11]伍良生,杨 勇,周大帅.机床主轴径向回转误差的测试与研究[J]. 机械设计与制造,2009(1):107-109.
(编辑 李秀敏)
The Accuracy Analysis of Error Separation for Two-point Separating Technique Method of Time Domain and Frequency Domain
MU De-qiang,CUI Bo,XIE Xin-wang,CHEN Yi
(School of Mechatronic Engineering, Changchun University of Technology, Changchun 130012, China)
In order to analysis the principle of error and the principle error’s regularity and characteristics in the two point error separation method of time domain and frequency domain. Established a part model to march the error separation, through the analysis of different influence factors found the principle error’s regularity and characteristics of two point method error separation technique, and compared the accuracy of two kinds of error separation technique.Using two kinds of error separation technique and roundness measuring instrument to measure the same parts, found that the experiment results and the results of simulation agree with the analysis of theory.So we can draw the conclusions: When the number of Samples—N expand 1 times,the ratio of the absolute error of the parameter value is getting closer to 2; with facing mounting the two sensors, the results of two point separation error is the smallest.;with same sampling parameters, the precision of error separation technique in frequency domain method is higher than error separation technique in time - domain method.
the two-point algorithm;error separation;principle error;influential factor;influencing rule
1001-2265(2014)07-0031-03
10.13462/j.cnki.mmtamt.2014.07.009
2013-12-14
吉林省科技厅重点科技攻关项目(2130206027GX)
母德强(1961—),男,辽宁昌图人,长春工业大学教授,博士,博士生导师,主要研究方向为精密加工及检测;通讯作者:崔博(1988—),男,吉林舒兰人,长春工业大学硕士研究生,研究方向为精密加工及检测,(E-mail)db0425@126.com。
TH161;TG65
A
