基于有限元与智能算法的工程陶瓷切削温度研究*

马廉洁，李 琛，曹小兵，陈小辉，单增瑜

(1.东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004; 2.东北大学 机械工程与自动化学院,沈阳 110819)

基于有限元与智能算法的工程陶瓷切削温度研究*

马廉洁1,2，李 琛1，曹小兵1，陈小辉1，单增瑜1

(1.东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004; 2.东北大学 机械工程与自动化学院,沈阳 110819)

以工程陶瓷切削过程为研究对象，通过DEFORM有限元分析、灰色系统和BP神经网络算法，研究了工程陶瓷切削温度特征。根据切削温度有限元仿真数据，构建了不等时距灰色预测模型，预测了工程陶瓷切削温度，在此基础上建立了两层BP神经网络，结合两种算法的优点，提高了预测精度。研究结果表明，切削开始阶段切削温度迅速达到峰值，随后趋于稳定。随着切削速度、进给速度、切削深度和主偏角的增加，切削温度均呈上升趋势，其中切削温度对切削速度最为敏感。

切削温度；灰色系统；BP神经网络；有限元；工程陶瓷

0 引言

切削过程所产生的切削热导致刀-屑接触面温度升高，直接影响加工表面质量和刀具使用寿命。陶瓷材料在切削过程中的冲击、振动较大，更加容易导致高温、高热现象发生。因此，其切削温度的研究更具实用价值。金属材料切削温度的研究一直比较活跃[1-2]，而陶瓷材料具有电绝缘、脆性大、难加工等特点，加工过程的温度测量难度更大，所以，相关的研究工作较少[3-4]。

Johnson-Cook模型是描述塑性材料去除过程的经典理论，长期以来，塑性材料加工的有限元仿真异常活跃[5-6]，但是该模型并不适合硬脆难加工材料。因此，工程陶瓷材料的机械加工有限元仿真的研究工作进展较为缓慢。针对这一技术瓶颈，本文从模型改进入手，建立了适合于陶瓷材料的本构模型，并将其在DEFORM有限元分析中实际应用，以此来研究陶瓷材料加工过程的温度特性。

人工神经网络具有很强的记忆、非线性映射、自学习等能力，在给定的训练样本范围之内，其预测精度较高，因此被广泛应用[7]。但是要求样本数量较大，同时在训练样本范围之外，预测误差会急剧增大。在很多情况下，这一缺点使得神经网络的作用失去了实际意义。灰色系统是一种研究少数据、贫信息不确定性问题的新方法，弥补了数理统计方法进行系统分析对样本数据量需求大的缺点，可避免量化结果与定性分析结果不符的情况[8]，不等时距灰色预测对单调的数据具有更理想的预测效果[9]。不仅如此，灰色系统对样本数据范围之外的预测结果，具有较高的精度。鉴于此，本文将BP神经网络和灰色系统两种算法融合，来研究工程陶瓷的机械加工过程中切削温度随工艺参数变化的规律。

1 陶瓷材料切削温度有限元仿真

车削时的切削热来源主要有两方面：一是切削层发生弹性变形和塑性变形所耗散的能量；二是切屑与刀具前刀面、后刀面间消耗的摩擦功。其中，切削用量对切削温度T影响较大。金属材料切削时，切削温度经验模型[10]如式(1) 所示(本文称之为经验模型)。

(1)

式中：x一般取0.26～0.41，vc为切削速度，f为进给量，ap为切削深度，CTv，CTf，CTap为相应的修正系数。

切削试验表明，切削温度不仅与切削速度vc，进给量f，切削深度ap有关，同时也与刀具主偏角κr有关，所以有限元分析主要研究四者同切削温度的关系。

图1c所示为切削温度变化过程，切削开始阶段刀具切削刃作用点的温度急剧上升，在0.000222s时温度达到一个峰值，此后的温度都在平均值的上下波动，这与切削温度定性分析结论比较一致。因此，仿真数据具有一定的实用价值。随工艺参数的变化，温度仿真结果如图4～图7所示。

(a)刀片温度 (b) 工件温度 (c)刀具温度仿真 变化过程图1 切削温度仿真

2 不等时距灰色系统的温度预测

2.1 不等时距灰色预测模型构建

假设原始数据序列为：

(2)

将间距作为乘子，对原始数据序列进行一次累加生成。得：

(3)

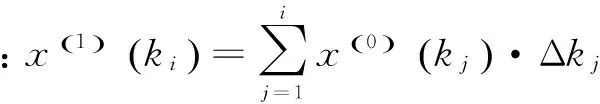
Δkj=ki-ki-1≠const，，其中i=2，3，…，n。

(4)

将微分方程离散化：

(5)

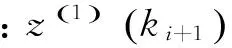
令：

用矩阵形式表示公式(5)，即：

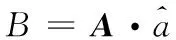
(6)

采用最小二乘法求解公式(6)得：

(7)

(8)

再将公式(8)累减还原，得原始数据的预测表达式：

(9)

其中，i=1,2，…，n

2.2 基于不等时距灰色系统的切削温度预测

切削温度-切削速度预测。如表1所示，其1～15组数据中，把前11组数据作为训练样本，后4组作为检验数据，检验后的最大误差为4.05%，说明模型具有较高的可靠性。据此预测更高切削速度下的温度，其预测结果如图4所示。

切削温度—进给速度预测。表1中，16～29组数据中，把前10组数据作为训练样本，以后4组数据作为检验数据，检验后的最大误差为0.7%，说明模型具有高的可靠性。据此预测更高进给速度下的温度，其预测结果如图5所示。

切削温度—切削深度预测。如表1所示，其30～42组数据中，把前10组数据作为训练样本，以后3组数据作为检验数据，检验后的最大误差为5.71%，说明模型具有一定的可靠性。据此预测更大切削深度下的温度，其预测结果如图6所示。

切削温度—主偏角预测。如表1所示，其43～50组数据中，把前6组数据作为训练样本，以后2组数据作为检验数据，检验后的最大误差为3.09%，说明模型具有高的可靠性。据此预测更大主偏角下的温度，其预测结果如图7所示。

表1 有限元仿真实验条件

3 基于BP神经网络的函数拟合

3.1 BP神经网络

BP神经网络是利用误差反向传播算法对网络进行训练，对网络权值和阈值沿着函数下降最快的方向(负梯度方向)进行修正，如式(10)所示。

xk+1=xk-akgk

(10)

式中：xk是当前的权值和阈值矩阵；gk是当前表现函数的梯度；ak是学习速率。

激活函数为：

(11)

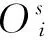
(12)

相应的输出状态为：

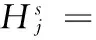
(13)

网络最终输出为：

(14)

误差为：

(15)

每一步的修正量为：

(16)

以上权值的修正量如式(17)。

(17)

3.2 BP神经网络构建

根据有限元仿真、灰色系统两类数据统一组合分析，建立两层BP神经网络，隐层神经元个数按切削速度、进给速度、切削深度和主偏角依次设为150、135、150、150个，输出层为1个神经元单元(如图2所示)。

图2 BP神经网络结构示意图

设隐层训练函数为tansig，输出层训练函数为purelin，后向传播网络的权值和阈值学习函数为learngdm，后向传播网络的训练函数为traingdx。最大训练代数为10000；训练速度为0.05；每10步记一次；训练误差为0.000001。网络训练误差如图3所示，神经网络拟合结果见图4～图7。

图3 神经网络训练误差

4 结果与讨论

4.1 切削速度对切削温度的影响

图4所示，随着切削速度的提高，切削温度明显上升。切削过程中，切屑沿前刀面流出，切屑底层与前刀面发生强烈摩擦，产生了切削热。这些摩擦热主要在切屑很薄的底层里产生，如果在连续流出的切屑中截取极短的一段作为一个单元来考察，当这个切屑单元沿前刀面流出时，摩擦热一面生成一面向切屑的顶面方向和刀具内部传导。如果切削速度提高，则摩擦热产生的时间较短，而切削热向切屑内部和刀具内部传导都需要一定的时间[10]，热量扩散不够及时。因此，随切削速度的提高，切削热在切屑底层大量积聚，从而使切削温度升高。图4中虚线所示为经验模型的计算曲线，当经验系数CTv取不同值时，曲线的趋势与预测趋势均不同，说明了硬脆性材料与金属材料切削温度特性存在差异。

图4 切削速度对切削温度的影响

4.2 进给速度对切削温度的影响

图5所示，随着进给量的增加，单位时间内的材料去除量增多，切削过程中产生的热也增多，使切削温度上升。但是切削温度随着进给量升高的幅度不如切削速率那么显著。这是因为单位切削力和单位切削功率随着进给量的增大而减小，去除单位体积材料产生的热量也减小，所以增大进给量时，较切削速度增加的慢一些。此外，当进给量增加后，切屑变厚，切屑的热容量增大，由切屑带走的热量也多，因此上升不是太显著。图5所示，虚线为经验模型的计算曲线，趋势与预测趋势不同，且与经验系数CTf取值无关。

图5 进给速度对切削温度的影响

4.3 切削深度对切削温度的影响

图6所示，切削深度在0.01mm～0.05mm的时候，温度上升比较迅速，在0.05mm以后升高较缓慢。与切削速度相比，切削深度对切削温度的影响显著性较低，这是因为切削深度增大以后，切削区产生的热量虽然增多，但因为切削刃参加工作的长度也增加了，改善了散热条件，所以切削温度升高趋势不是太大。图6所示，虚线为经验模型的计算曲线，趋势与预测趋势不同，且与经验系数CTap取值无关。

图6 切削深度对切削温度的影响

4.4 主偏角对切削温度的影响

图7所示，随着主偏角的增大，切削温度将逐渐升高，这是因为主偏角增大后，切削刃的工作长度缩短，使切削热相对集中，而且主偏角加大，刀尖减小，使散热条件变差，从而提高了切削温度。反之，适当减小主偏角，使刀尖角加大，切削刃工作长度增加，散热条件改善，从而使切削温度也降低。

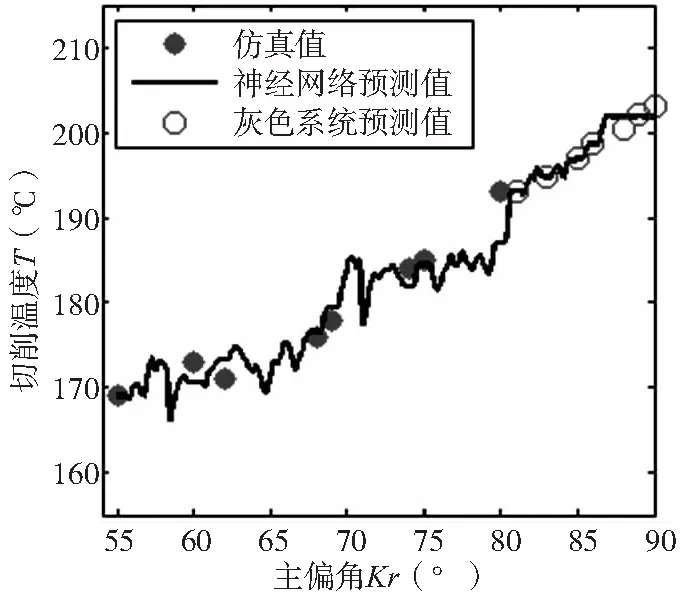
图7 主偏角对切削温度的影响

5 结论

(1) DEFORM-3D切削温度有限元仿真结果表明，切削开始阶段切削温度急剧上升，迅速达到峰值，随后趋于稳定，在平均值上下波动。

(2) 基于有限元仿真数据，利用灰色系统预测对有限元数据进行了更大范围补充，以弥补神经网络预测的不足,误差范围在0.7%～5.71%之间。并建立两层BP神经网络，进行了神经网络函数拟合。

(3) 研究结果表明，随切削速度、进给量、主偏角、切削深度的增加，切削温度均呈上升趋势，但上升速率有所不同。

[1] Leshock C E, Shin Y C. Investigation on cutting temperature in turning by a tool-work thermocouple technique[J]. Transactions of the ASME, Journal of Manufacturing Science and Engineering,1997, 119:502-508.

[2] 盛精,黄丛林,刘超,等.基于切削温度的切削用量优化的实践与研究[J].中国机械工程, 2012,23(17):2066-2070.

[3] 田欣利,李富强,王朋晓,等. Si3N4 陶瓷激光加热辅助引弧微爆炸加工温度场仿真[J].中国机械工程,2013,24(19):2557-2561.

[4] 马廉洁,单增瑜,庞正,等.玻璃陶瓷切削效率多元回归数值模拟研究[J].组合机床与自动化加工技术, 2013(6):113-115.

[5] 董岚枫,钟约先,马庆贤,等.大型水轮机主轴锻造过程裂纹缺陷的预防[J].清华大学学报,2008,45(5):765-768.

[6] 何俊,夏斌.TC4钛合金超声波椭圆振动切削仿真研究[J].组合机床与自动化加工技术, 2013(11):17-20.

[7] 奚立峰,黄润青,李兴林,等.基于神经网络的球轴承剩余寿命预测[J].机械工程学报,2007,43(10):137-143.

[8] 伏玉笋,田作华,施颂椒.灰色系统理论、数据预处理及其应用[J].上海交通大学学报,2001,35(2):288-271.

[9] 江龙平,徐可君.疲劳裂纹三维动态扩展灰色系统预测[J].机械工程学报,2006,42(1):86-89.

[10] 周泽华.金属切削原理[M].上海:上海科学技术出版社,1993.

(编辑 李秀敏)

Cutting Temperature of Engineering Ceramics Based on Finite Element and Intelligent Algorithms

MA Lian-jie1,2, LI Chen1, CAO Xiao-bing1, CHEN Xiao-hui1, SHAN Zeng-yu1

(1.School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao Hebei 066004, China;2.School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China)

The object of study is engineering ceramics cutting process, the temperature characteristic of engineering ceramics was studied respectively by finite element analysis - DEFORM software, gray system and BP neural network algorithm. The unequal interval gray prediction model, was established based on the two-tier BP neural network, which simulated the cutting temperature in the paper. Combining the advantages of two algorithms, the prediction accuracy was improved. The results indicated that the temperature quickly reached a peak in beginning of cutting, and then stabilized, the cutting temperature was increased with increasing of cutting speed, feed speed, cutting depth and main angle. The influence of cutting speed on cutting temperature was most significant.

cutting temperature; gray system; BP neural network; finite element simulation; engineering ceramics

1001-2265(2014)07-0001-04

10.13462/j.cnki.mmtamt.2014.07.001

2014-03-06；

2014-04-01

国家自然科学基金项目资助(51275083)

马廉洁(1970—)，男，内蒙古赤峰人，东北大学副教授，硕士生导师，主要研究方向为硬脆材料加工理论与技术，(E-mail)mlj@mail.neu.edu.cn。

TH161;TG65

A