基于W态和EPR对受控概率隐形传输类团簇态
2014-07-18杨本朝
杨本朝, 曾 光
(信息工程大学 数学工程与先进计算国家重点实验室 河南 郑州 450002)
基于W态和EPR对受控概率隐形传输类团簇态
杨本朝, 曾 光
(信息工程大学 数学工程与先进计算国家重点实验室 河南 郑州 450002)
提出一个利用部分纠缠EPR对和W态作为量子信道,在可信第三方(Charlie)的控制下,发送方(Alice)进行3次Bell基测量、一次Hadmard变换和单粒子测量,接收方(Bob)引进一个辅助粒子,进行相应的幺正操作,则可以以一定的概率实现类团簇态的隐形传输.
隐形传输; 幺正变换; 类团簇态
0 引言
自1993年Bennett等人提出量子隐形传态(teleportation)的概念[1]以来,量子隐形传态在理论和实验上都取得了长足进展, 在此基础上,任意二粒子和三粒子纠缠态的隐形传态基本上得到了解决[2-7]. 2001年,Raussendorf和Briegel提出了当粒子数大于等于4时, 类团簇态具有一些GHZ类态和W类态所没有的特殊性质,并具有更强的退纠缠性[8]. 近年来,类团簇态的制备和隐形传态已经引起了人们的关注.
文[9]中给出了用4对EPR对共8个粒子纠缠态的量子信道实现隐形传送四粒子类团簇态的方案;文[10]中提出了用7个粒子最大纠缠态作为量子信道的传送方案,但实际中由于量子态和周围环境的相互作用不可避免,而且实验制备的纠缠态大都是非最大纠缠态. 因此,本文提出了一种以部分纠缠的EPR对和W态作为量子信道,用7个粒子非最大纠缠态实现四粒子类团簇态的量子受控概率隐形传态方案. 与上述方案相比,本方案节省了1个粒子资源,采用了具有一般意义的非最大纠缠态,更具实验操作性.
1 类团簇态的概率隐形传态
假设Alice要传送类团簇态
(1)
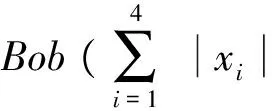
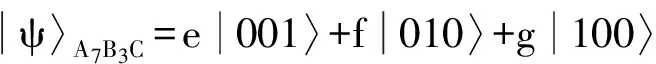
(2)
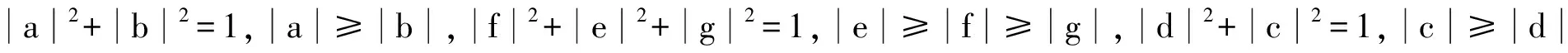
整个系统的态可以表示为
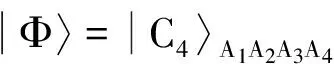
(3)
其中Alice拥有粒子(A1,A2,A3,A4,A5,A6,A7),控制者Charlie拥有粒子C,粒子(B1,B2,B3)归Bob所有.
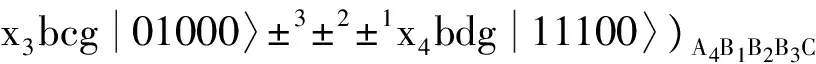
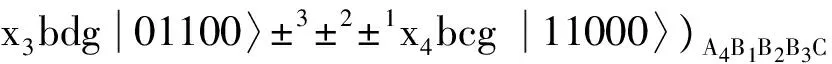
(5)
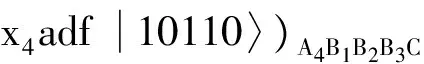

(7)
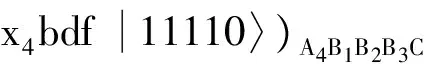
(8)
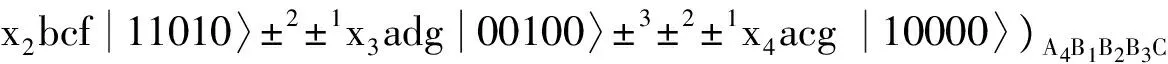
(9)
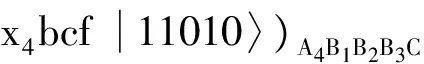
(10)
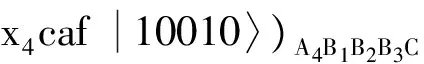
(11)
这里的4个Bell态为:
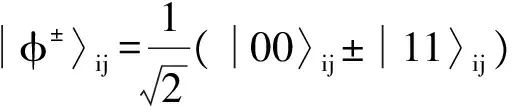
(12)
其中,±3,±2和±1中的上标分别对应于由粒子(A1,A7),(A2,A5)和(A3,A6)组成的Bell态.接着,Alice对粒子A4施行Hadamard操作
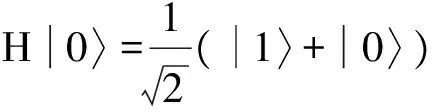
(13)
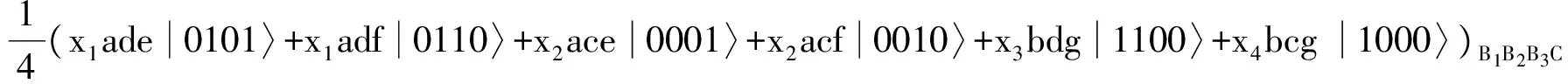
(14)

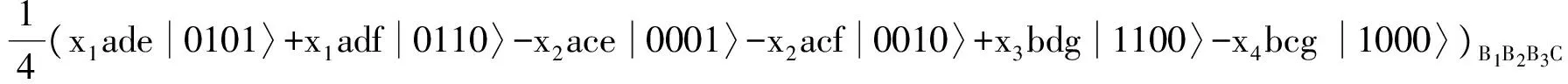
(15)
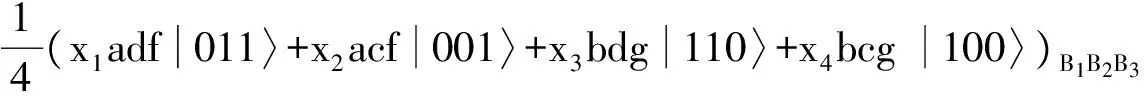
(16)
U1=(σx)B2⊗(σx)B3⊗(CONT)B2B4⊗(SWAP)B2B3,
则将(14)式中的态变换为
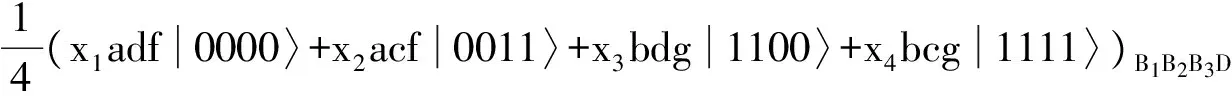
(17)
对于其他的情况,在表1中给出了涉及到的所有可能的操作.其中,σx,σy,σz是Pauli矩阵,(CONT)BiBj是以粒子Bi为控制比特,粒子Bj为目标比特进行的控制—非操作,(SWAP)BiBj是对粒子Bi,Bj执行二元交换门操作.

表1 Alice和Bob需要做的所有操作Tab.1 Bob’s operations according to Alice’s results
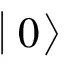
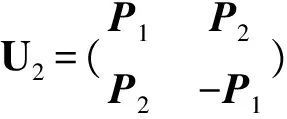
(18)
其中Pi(i=1,2)是一个4×4的矩阵,可以表示为
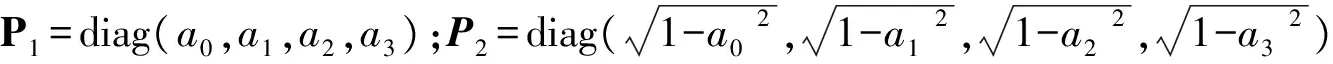
(19)
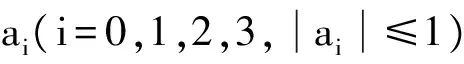
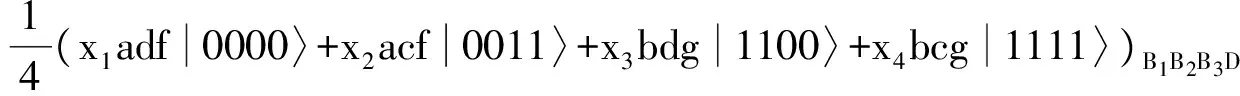
变换为:
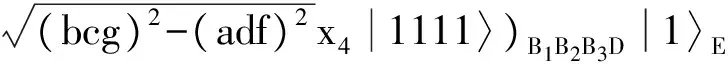
(20)
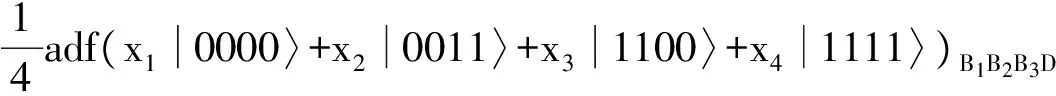
(21)

表2 各种情况下a0,a1,a2,a3,a4的取值Tab.2 The values of a0,a1,a2,a3,a4
2 结论
本文以部分纠缠的EPR对和W态为量子信道,隐形传送一个在量子信息的应用中比GHZ态和W态更有使用价值的四粒子类团簇态.发送方经过一系列测量操作,在可信第三方的控制下,接收方引进一个辅助粒子,进行相应的幺正变换后,可以一定的概率实现该隐形传输.
[1] Bennete C H, Brassard G, Crépean C, et al. Teleporting an unknown state via dual classical and Einstein-Podolsky-Rosen channels [J]. Phys Rev Lett, 1993, 70(13): 1895-1899.
[2] 温巧燕,郭奋卓,朱甫臣. 量子保密通信协议的设计与分析 [M]. 北京:科学出版社,2009.
[3] 马蕴超,徐明东. 远程制备三粒子纠缠态 [J].量子光学学报,2004, 10(4): 153-156.
[4] 杨本朝,韩学锋. 一般WGHZ态的概率隐形传输 [J]. 郑州大学学报:理学版,2012,44(4):55-58.
[5] Dai H Y, Li C Z, Chen P X.Probabilistic teleportation of an arbitrary three particle state via a partial entangled four-particle state and a partial entangled pair [J]. Chin Phys, 2003, 12(12): 1354-1359.
[6] Xiong X S, Fu J, Shen K, et al. Controlled teleportation of an unknown two-particle partly entangled state [J]. Acta Photonica Sinica, 2006, 35(5):780-782.
[7] 杨本朝, 张昭, 王洪. 利用 Cluster 态实现三粒子纠缠 GHZ 态的概率隐形传态 [J]. 信息工程大学学报, 2012, 13(5): 540-543.
[8] Bregel H J, Raussendorf R. Persistent entanglement in arrays of interacting particles [J]. Phys Rev Lett, 2001, 86(5):910-913.
[9] 洪智慧,聂义友,易小杰,等. 四粒子团簇态的量子隐形传态[C]//2007年全国第16届13省(市)光学学术会议.拉萨,2007.
[10]陈智鹏,李渊,胡之惠,等. 利用GHZ态和EPR态隐形传送四粒子团簇态 [J]. 上海电机学院学报,2010,13(3):135-139.
[11]Zhang Xiaoqui, Li Hongmei, Zeng Haosheng, et al. Teleportation of multi-qubit entangled states [J]. Chin Phys Lett,2006, 23(11):2900-2902.
Probabilistic Teleportation of the Cluster StateBased on W State and EPR Pairs
YANG Ben-chao, ZENG Guang
(KeyStateLaboratoryofMathematicalEngineeringandAdvancedComputing,InformationEngineeringUniversity,Zhengzhou450002,China)
A scheme of teleportation of the cluster state was presented when a non-maximally entangled W state and two EPR pairs were used as quantum channels. With the help of Charlie, the teleportation could be successfully realized with a certain probability by performing three Bell measurements and a Hadmard operation on the sender’s side, and by introducing an auxiliary particle and performing unitary transformations on the receiver’s side.
probabilistic teleportation; unitary transformation; cluster state
2013-06-30
杨本朝(1981-),男,助教,主要从事量子密码协议研究,E-mail:yang_benchao@aliyun.com.
O 431.2
A
1671-6841(2014)01-0068-05
10.3969/j.issn/1671-6841.2014.01.016
