双边生灭过程的轨道结构与Motoo理论
2014-07-18薛玲霞
陈 丽, 薛玲霞
(1.郑州师范学院 数学与统计学院 郑州 450044;2.郑州旅游职业学院 基础部 郑州 450009)
双边生灭过程的轨道结构与Motoo理论
陈 丽1, 薛玲霞2
(1.郑州师范学院 数学与统计学院 郑州 450044;2.郑州旅游职业学院 基础部 郑州 450009)
主要研究双边生灭过程的轨道结构和构造理论中的生灭过程与Motoo理论之间的对应关系,并且说明了构造理论中各个参数的概率含义.
双边生灭过程; Ray-Knight紧化; 右过程; Motoo理论
0 引言
文献[1-2]利用Markov过程中的一般理论刻画了生灭过程的轨道结构:从(-)是流入的,(-)是流出的,(-)是自然的,(-)是正则的等几个方面指出双边生灭轨道结构与构造理论之间的对应关系,本文在文献[1-2]的基础上,继续给出和-都是流出的情况下双边生灭过程的轨道结构和构造理论,并研究生灭过程与Motoo理论之间的对应关系,说明双边生灭过程构造理论中各个参数的概率含义.
1 预备知识
设E={…,-2,-1,0,1,2,…},ai,bi,i=0,±1,±2,…是一组正数,Q=(qi,j)是E上的双边生灭矩阵,其中

如文献[1-2],定义Q的自然尺度zi,i=0,±1,±2,…如下:
z0=0,

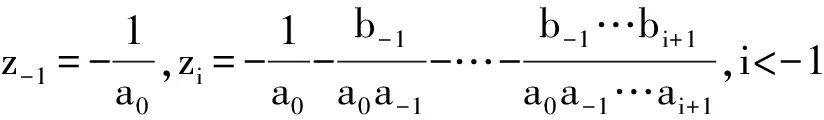

定义标注测度μi,i=0,±1,±2,…,如下:
(1)
令
(2)
在R-,R,S-,S分别取有限和无限的情况下,把-和分为正则、流入、流出和自然4种情况.并且对于任意的i∈E,令xi=Ei{e-λσ0},yi=Ei{e-λσ},ωi=Ei{e-λσ-}.这些量都是由Q的最小过程唯一确定的.
在文献[1-2]中,讨论了和-在一些特殊情况下的轨道结构和构造理论,本文利用Motoo理论及文献[3-5]继续讨论在其他情况下的轨道结构和构造理论.
2 Mootoo理论简介
设S是一个Lusin空间,X=(Ω,R,Rt,Xt,θt,Px)是一个状态空间为S的Hunt过程,即X满足假设:
1)X的轨道是右连左极的;
2)滤子{Rt}是右连续的;

4)X满足正规性,即Px{X0=x}=1,∀x∈E;
5)对于任意的X的α-过分函数f(·),过程{f(Xt)}t≥0是右连续的;
6)X是拟左连续的.
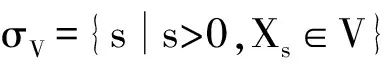
令φ(x)=Ex{e-σ},x∈S.存在唯一的可加泛函{Lt},使得
φ(x)=Ex{∫(0,)e-sdLs},∀x∈S,
(3)
并且Lebesgue-Stieltjes测度dL(ω)的支撑几乎必然等于Z(ω),{Lt}称为X在V上的局部时.
由文献[6],存在V上的函数l(·),使得
∫(0,t)IV(Xs)ds=∫(0,t)l(Xs)dLs
(4)
存在(Ω,R)上的σ有限测度族P(x,·),x∈V,使得对于任意的x∈E,F∈R及可料过程{Zt},有
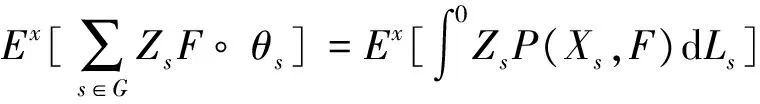
(5)
并且对于任意的{Rt}停时T,B∈R,Λ∈RT,
P(x,IΛ·IB∘θT)=P(x,IΛ·EXT{IB}),
(6)
P(x,·),x∈V称为X在V上的游程测度,式(6)说明游程测度具有强Markov性.(P,L)称为X在V上的流出系统.此外,P(x,·)还满足方程
P(x,1-e-σ)=1.
(7)


ωα(x)=P(x,(1-e-ασ)I{x}(Xσ)),∀x∈V,
(8)

(9)


(10)
对于任意的x∈S,f∈B+(S),有

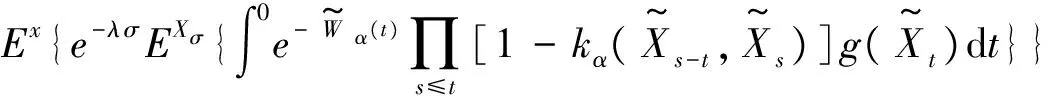
(11)

3 生灭过程与Motoo理论
文献[3]给出了-和都是流出的, 而生灭过程的豫解式Rij(λ)诱导的Ray-Knight紧化的附加点有两个或一个,其中只有一个是正则点的情况.在本文中假定:
1)-和都是流出的,Rij(λ)是密度矩阵为生灭矩阵Q的诚实的豫解式;
2)E在Rij(λ)下的Ray-Knight紧化为E∪{-,};
3)对Rij(λ)诱导的右过程X=(Ω,R,Rt,Xt,θt,Px)来说,-和都是非分支点.
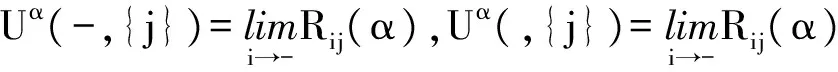

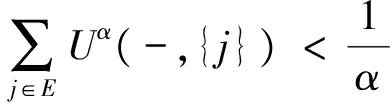
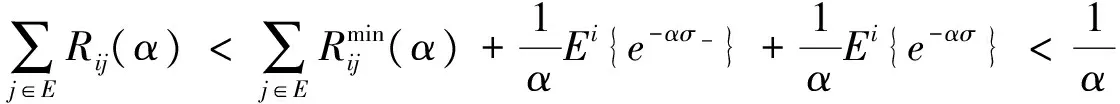
与Rij(λ)是诚实的豫解式矛盾.所以



所以
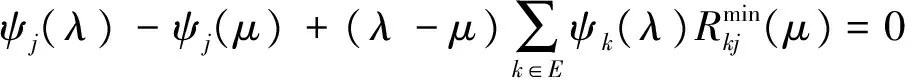



由文献[3]中引理3,(ψj(λ),j∈E)满足方程组
(12)
但由于-和都是流出的,由文献[3]中引理4,方程组(12)只有零解,矛盾.所以P{τ=0}=1,即是右过程X=(Ω,R,Rt,Xt,θt,Px)的正则点.同理-也是正则点.
由于-和都是正则点,所以V的首中时和首达时几乎必然相同,也和马氏链的爆炸时间相等,即σV=σ,此外,由于生灭矩阵Q有两个Martin积极流出边界-和,在t→σ-时,最小过程的极限也有两种情况,所以Martin积极流出边界-和Ray-Knight紧化中的极限相同,也是-和,所以-和既是Martin积极流出边界,又是Ray-Knight紧化中的附加点.
令V={-,}.由式(3),存在X的可加泛函Lt使得

由于


由游程测度P(x,·),x∈V的强Markov性(6),则
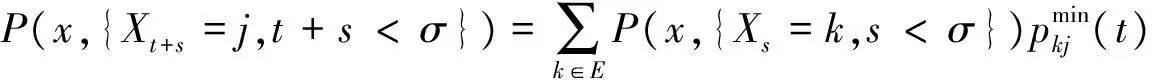
令

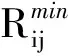


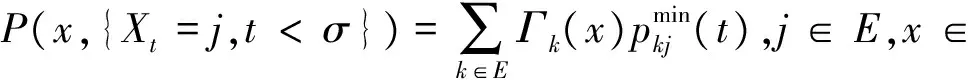
由式(7)可得
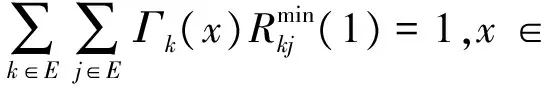
(13)
由式(8),有

即

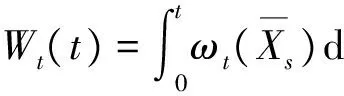

令


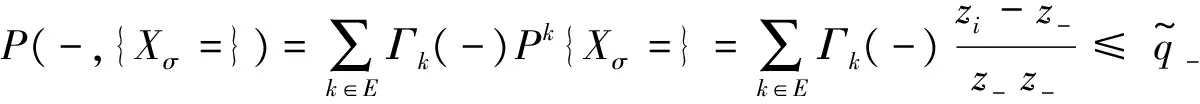
(14)

(15)
由式(10)容易得出
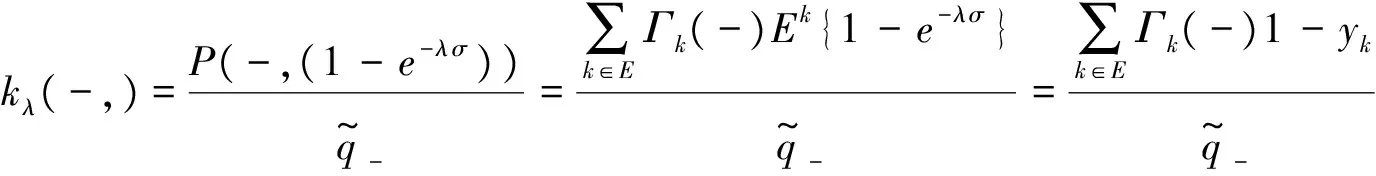
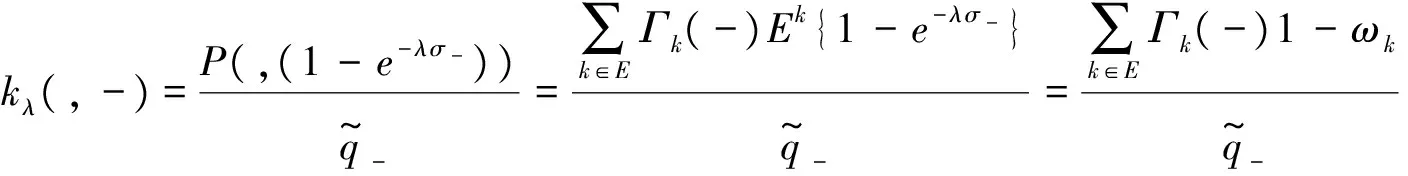
将这些量带入式(11),有定理1.
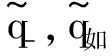

(16)
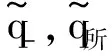
[1] 陈丽,薛玲霞,兰社云,等.双边生灭过程的轨道结构和构造理论[J].河南大学学报:自然科学版,2012,42(4):337-342.
[2] 陈丽,薛玲霞.双边生灭过程的轨道结构和构造理论(II)[J].河南大学学报:自然科学版,2013,43(1):5-10.
[3] 杨向群.可列马尔科夫过程构造论[M].长沙:湖南科学技术出版社, 1986: 34-205.
[4] 侯振挺,郭青峰.齐次可列马尔科夫过程[M].北京:科学出版社,1980:55-69.
[5] 吕芳,王燕.Ito游程理论下的生灭过程的构造[J].郑州大学学报:理学版,2012,44(3):65-71.
[6] 吕芳.生灭过程自有限态“流入”的轨道性质[J].信阳师范学院学报:自然科学版,2011,24(3):49-55.
[7] 候贤敏,李巧利.生灭过程的Ito 复合定理[J].郑州大学学报:理学版,2011,43(4):23-30.
Paths of Bi-lateral Birth-death Process and Theory of Motoo
CHEN Li1, XUE Ling-xia2
(1.SchoolofMathematicsandStatistics,ZhengzhouNormalUniversity,Zhengzhou450044,China;2.DepartmentofBasic,ZhengzhouTourismCollege,Zhengzhou450009,China)
The orbits of bi-lateral birth-death process and the structures of the general theory of Markov processes were discussed, the corresponding relation between birth-death process and Motoo theory was studied, and the probability meaning of each parameter in the structure was given.
bi-lateral birth-death process; Ray-Knight compactification; right process; Motoo theory
2013-07-15
郑州师范学院校级项目,编号 2012083.
陈丽(1968-),女,副教授,硕士,主要从事概率论研究,E-mail:clxuu6697@sina.com.
O 211.62
A
1671-6841(2014)01-0042-05
10.3969/j.issn/1671-6841.2014.01.010
