基于Bootstrap方法的分布未知情况下的小波动过程质量控制
2014-07-18王海宇
王海宇
(中原工学院 经济管理学院 河南 郑州 450007)
基于Bootstrap方法的分布未知情况下的小波动过程质量控制
王海宇
(中原工学院 经济管理学院 河南 郑州 450007)
讨论了在质量特性分布未知的情况下对小批量生产过程中产生的较小异常波动进行监控的一种Bootstrap WV-EWMA控制图设计方法.首先引入赋权方差法将任意未知分布转换为两个正态分布,由此构造WV-EWMA控制图.然后通过对有限样本进行多次随机有放回抽样的Bootstrap方法对未知分布的集中和离散程度进行较为有效的统计估计,由此建立能够对分布未知的小批量过程进行质量监控的Bootstrap WV-EWMA方法.以平均运行长度ARL(average run length)为监控效率的衡量指标,提出了这种小波动控制图方法的优化参数设计方案,并通过与已有的方法进行对比说明这种方法的有效性.
过程质量控制; Bootstrap方法; EWMA控制图
0 引言
在当今快速多变的市场竞争中,生产制造过程逐步呈现出由传统的大批量生产向多品种小批量生产转变的趋势.在多品种小批量生产环境中,无法像大批量生产过程那样抽取大量的样本来确定数据的统计分布,更不能精确估计均值和标准差.若直接利用传统方法对小样本质量过程建立控制限,会造成虚发警报的概率显著增大,从而导致无谓的调整次数增多,干扰正常的产品生产过程[1].文[2]最早提出了小样本均值极差控制图,文[3]利用概率积分变换方法将小样本观测值转换成标准正态分布,提出了Q控制图.文[4]提出了工序相似性评判的方法将多个小批量过程转换为近似的大批量过程进行质量监控.文[5]将编码相同的工序划分为同一个虚拟工序,再用传统控制图方法进行监控.文[6]应用贝叶斯统计推断的方法对分布参数未知的正态小批量过程构造先验质量控制模型.但是这些方法都需要先进行较为繁杂的转换运算,不利于生产实践的实时应用.近年来,Bootstrap方法受到了国内外专家的广泛关注,该方法只依赖能获得的少量样本来模拟大样本进行统计分析,弥补了传统方法中的不足.文[7]首先提出了Bootstrap控制图的概念,王晶等探讨了正态分布假定条件下小批量生产过程的Bootstrap控制图的应用[8].但上述研究仍然假定过程服从分布参数未知的正态分布,而对于非正态过程,尤其是那些没有先验数据判断过程分布的类型的情况,上述研究方法则难以有效应用.本文将针对这一问题,探讨采用赋权方差法分析构建分布类型不确定情形下的非对称小波动EWMA控制图,进而通过Bootstrap方法用少量样本对总体进行较精确的统计推断,构造Bootstrap WV-EWMA控制图方法,以有效对分布未知情况下的小批量生产过程进行质量监控.
1 赋权方差(WV)法
Choobine和Ballard最早提出用赋权方差(WV)法将非正态分布转换为正态分布[9],本文则将该方法应用在对未知分布进行正态性转换.假设一未知分布f(x)具有未知参数均值μ和标准差σ,如图1(a).将该未知分布从均值的位置分成两个部分,每一部分都分别作为两个不同的正态分布的一半,将这两个正态分布补齐,形成图1(b)和(c)的两个分布fL(x)和fU(x),它们具有相同的均值μ和不同的标准差σL和σU.图1(d)和(e)为fL(x)和fU(x)分别转换后的正态分布φ(x,μ,σL)和φ(x,μ,σU),其概率密度函数分别为φ(x,μ,σL)=φ((x-μ)/σL)/σL,φ(x,μ,σU)=φ((x-μ)/σU)/σU[10],这两个分布分别用来计算控制图的上下控制界限.

图1 赋权方差法Fig.1 Weighted variance method
2 分布未知情况下的WV-EWMA控制图
设X1,X2,…是相互独立的随机变量序列,则EWMA统计量Zi为
Zi=λ(Xi-μ)+(1-λ)Zi-1, 0<λ≤1,i=1,2,…,
(1)
其中,Z0=μ,λ为EWMA平滑系数.
由EWMA控制统计量中的权重特点,可以得到EWMA控制统计量Z的数学期望E(Z)和方差D(Z)分别为:
E(Z)=E(X)=μ;D(Z)=(λ/(2-λ))[1-(1-λ)2i]D(X),
(2)
当i比较大以后,方差就趋向于一个常数,D(Z)=(λ/(2-λ)n)σ,其中n为样本容量.

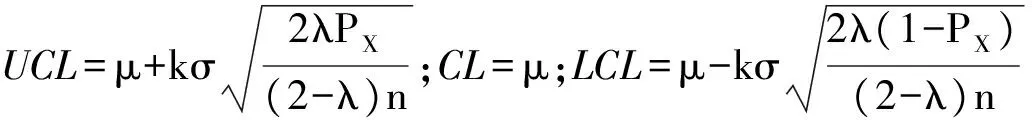
(3)
其中,k为控制线参数,在常规控制图中,通常取k=3.

3 基于Bootstrap方法的WV-EWMA控制图
在式(3)中,均值μ、标准差σ和比例系数PX的估计准确与否将直接决定控制图的使用效果,因此对于多品种小批量的生产环境,有必要采用Bootstrap方法进行参数估计.Bootstrap是一种只能获得少量样本情况下的统计估计,它是一种以原始数据为基础的模拟抽样统计推断方法,通过重采样来扩充样本容量并进行统计推断.设对于某未知的小批量过程采集了数量为m的随机样本集,T0={x1,x2,…,xm},其中xi为该分布的独立随机样本.对样本T0进行反复重采样,即有放回的抽取B个样本容量为n的随机样本,通过对这些样本数据的统计分析来对各类统计量如均值、方差等进行近似.如果B取足够大,那么通过从T0中重复抽样,就可以为各类统计量获得比较精确的估计和推断结果.在实际应用中,只需抽取B=1 000个左右Bootstrap样本即可[11].
Bootstrap WV-EWMA图可以由6个步骤设计完成:
1)对待监控的生产过程,抽取少量的d个样本容量为n的观测值作为原始样本,
T0={x11,…,x1n,x21,…,x2n,…,xd1,…,xdn}.
2)对样本T0进行有放回反复重采样,抽取B≥1 000个样本容量为n的Bootstrap样本Ti,i=1,2,…,B.
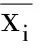

6)计算控制限.将比例系数PX的值代入式(3),就可以得到控制图的控制界限.
4 Bootstrap WV-EWMA图的优化设计
平均运行长度ARL(average run length)常常被用于控制图监控效率的评价指标,是指从过程出现异常波动到该异常被控制图发现之间的样本个数.对于EWMA图,文[12]提出采用积分计算的方法估计运行长度的分布情况,文[13]则提出用马尔可夫链的方法来研究平均运行长度.而对于未知分布下的EWMA图,由于其控制线的不确定性,难以使用积分计算的方法,因此本文采用马尔可夫链的方法来研究平均运行长度,具体计算方法参考文献[14].根据平均运行长度的计算方法可以设计出效果最优的监控方案,其原则是:当过程处于受控状态时,平均运行长度应该尽可能的大,通常为和常规控制图保持同样的错误报警概率,取受控状态的平均运行长度ARL0=370;当过程中发生了不可以接受的偏移时,平均运行长度应该尽可能的小,以尽快地发现出现的偏移,减少其带来的损失.表1给出了在PX分别为0.3,0.4,0.5,0.6,0.7几种情况下对于不同的偏移量l(偏移程度以标准差的倍数来统一度量)的最优设计参数(Bootstrap仿真抽样和平均运行长度的计算可以通过Matlab语言编程获得).

表1 Bootstrap WV-EWMA图优化方案(ARL0=370)Tab.1 The optimal design schemes of Bootstrap WV-EWMA
5 监控效率比较
本文把上面提出的设计方案与其他一些过程监控方案进行简单的比较,包括常规的均值极差控制图、EWMA控制图、Q图等.表2是通过仿真PX分别是0.5和0.6情况下,小批量样本数据计算各种监控方法平均运行长度进行比较的结果.
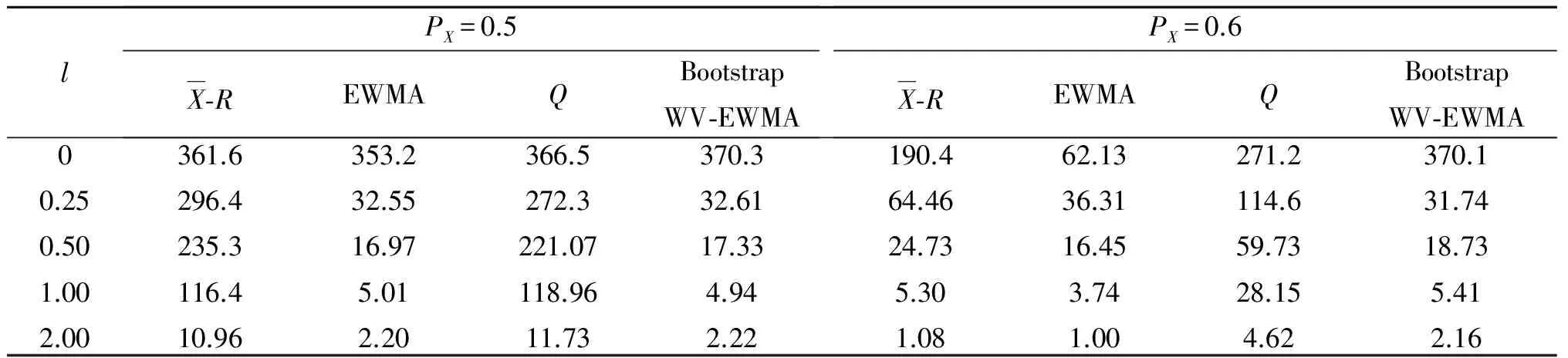
表2 未知分布情况下4种监控方法的平均运行长度Tab.2 ARL of four control charts for unknown distribution

6 应用实例
某零件生产过程中,要求钻孔直径为24.3±0.5 μm,现从生产过程中每隔20 s抽取4个产品,共抽取6个样本进行检测,结果见表3.

表3 原始观测数据Tab.3 The original observation data
按照未知分布下的Bootstrap WV-EWMA控制图实施步骤:
1)首先,对表3中的原始数据进行有放回重复抽样,共抽取1 000个样本容量为4的Bootstrap样本;
2)分别计算样本均值和样本方差,由于数据过多,文中不再一一列出.

5)计算EWMA控制图的控制界限.由表1可知,PX的值近似取0.7,于是有平滑系数λ=0.2,控制限参数k=2.5,就可计算控制界限为:


6)用于过程质量监控.按照控制界限进行绘图,以样本容量为4采集现场的实时数据,计算样本均值进行描点,如图2所示.

图2 钻孔直径的未知分布Bootstrap WV-EWMA控制图Fig.2 Bootstrap WV-EWMA chart of drill diameter
7)过程异常判断.Bootstrap WV-EWMA控制图的判异准则与一般的EWMA图的判异准则一致,如果图中每次描点都处于上下控制限之间,类似于本例中的情形,则可以认为过程处于稳定状态,不需要对过程进行干扰,继续正常生产及采样监控;而一旦出现有点超出上下控制限,则表示过程已经出现异常,应立即采取措施,查明并消除异常发生的原因.
7 结论
多品种小批量生产条件下,由于无法获取足够多的样本以有效估计过程总体的分布状况,传统控制图方法也就不能有效地建立和实施.本文将Bootstrap方法和赋权方差方法应用到小波动EWMA控制图的建立过程中,以此构造更符合小批量生产环境的控制图技术,并通过实证分析验证了这种方法的有效性.
[1] 杨旭. CIMS环境下小批量统计过程质量理论和方法的研究 [D]. 哈尔滨:哈尔滨工业大学, 2001.
[2] Hillier F S.XandRchart control limits based on a small number of subgroups [J]. Journal of Quality Technology, 1969, 1(1): 17-26.
[3] Quesenberry C P. SPCQ-charts for start-up processes and short or long runs [J]. Journal of Quality Technology, 1991, 23(3): 213-224.
[4] 余忠华,吴昭同. 面向小批量制造过程的质量控制方法研究 [J]. 机械工程学报, 2001, 37 (8): 60-64.
[5] 王丽颖,孙丽,王秀伦. 基于虚拟工序的小批量工序质量控制方法研究 [J]. 计算机集成制造系统, 2006, 12(8):1263-1266.
[6] Willemain T R. Designing control charts using an empirical reference distribution [J]. Journal of Quality Technology, 1996, 28(1): 31-38.
[7] 朱慧明,韩玉启. 小批量生产的贝叶斯质量控制模型 [J]. 运筹与管理,2003, 12(5): 66-70.
[8] 王晶,何桢,李范. 面向多品种小批量生产过程的Bootstrap控制图 [J]. 工业工程,2009, 12(2): 64-67.
[9] Choobine F, Ballard J L. Control-limits of QC charts for Skewed distribution using weighted-variance [J]. IEEE Transactions on Reliability, 1987, 36(1): 473-477.
[10]Castagliola P.X-bar control chart for Skewed populations using a scaled weighted variance method [J]. International Journal of Reliability, Quality and Safety Engineering, 2000, 7(3): 237-252.
[11]Efron B, Tibshirani R J. An Introduction to the Bootstrap [M]. New York: Chapman & Hall, 1993.
[12]Crowder S V. A simple method for studying run-length distributions of exponentially weighted moving average charts [J]. Technometrics, 1987, 29(4): 401-407.
[13]Lucas J M, Saccucci M S. Exponentially weighted moving average control schemes: properties and enhancements [J]. Technometrics, 1990, 32(1): 1-12.
[14]王海宇,徐济超,杨剑锋.非正态总体下控制图的优化设计 [J]. 系统工程理论与实践,2007, 27(1):125-130.
Process Quality Control for Small Shifts with Unknown DistributionBased on Bootstrap Method
WANG Hai-yu
(Economics&ManagementSchool,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)
A Bootstrap EWMA control chart used for monitoring smaller abnormal fluctuation of unknown distribution for short run production was discussed. At first, weighted variance method was introduced to split an unknown distribution into two normal distributions and to construct a kind of WV-EWMA control chart. And then Bootstrap method was proposed to evaluate parameters of the unknown distribution and to construct Bootstrap WV-EWMA control chart. Using ARL as a performance assessment method, optimal parameters design scheme of this chart was proposed and the effectiveness of this chart was illustrated by comparing with other control charts.
statistical process control; Bootstrap method; EWMA chart
2013-05-15
国家自然科学基金资助项目,编号71002073.
王海宇(1979- ),男,副教授,博士,主要从事统计质量控制研究,E-mail:wanghy1979@126.com.
TB 114.2
A
1671-6841(2014)01-0063-05
10.3969/j.issn/1671-6841.2014.01.015
