环帆伞可变参数对设计偏差的灵敏度分析
2014-07-18甘和麟荣伟
甘和麟 荣伟
(北京空间机电研究所,北京 100094)
0 引言
因为具有高可靠性、稳定性强的特点,航天器特别是大型航天器的回收着陆应用中的主伞大都是环帆伞,如“双子星座”、“水星号”、“阿波罗”飞船、“神舟”系列飞船等[1-3]。环帆伞在设计之初,需要根据设计指标确定伞衣的名义尺寸并指定基本构型,之后再以名义尺寸和基本构型为基础,逐步确定环帆伞的各个结构参数尺寸,最终得到尺寸完备的实际伞衣结构并投入生产。在这一过程中,受到强度要求、模型简化、工艺限制、舍入误差等因素的影响,设计得到的伞衣面积、结构透气量与设计之初给定的名义面积与结构透气量之间会产生差异[4-5];如果差异过大,设计人员就不得不对伞衣幅的结构参数采用“试凑”的方式进行调整。文献[1]对部分参数的作用规律进行了简要说明,却未对相关调整项的调整效果进行分析,因而在实际工作中可能需要经过多次试凑方能得到各方面都较为满意的结果。如果在进行调整的时候,对各调整参数灵敏度有较为精确的了解,就可以有针对性的、用高灵敏度参数对设计结果进行粗调,用低灵敏度参数进行细调,减少调整的次数,提高设计工作的效率。以此为目的,本文将对环帆伞设计过程中可变参数的灵敏度进行讨论和分析。
1 可变参数定义
对设计流程进行分析发现,大多数结构参数的组成都是有规律的。这些组成因子一部分由任务约束条件直接给定或继承其他参数,可看作是输入因子;另一部分则往往由经验系数或经验公式的形式给出,表征该参数与输入因子之间的关系,见图1。
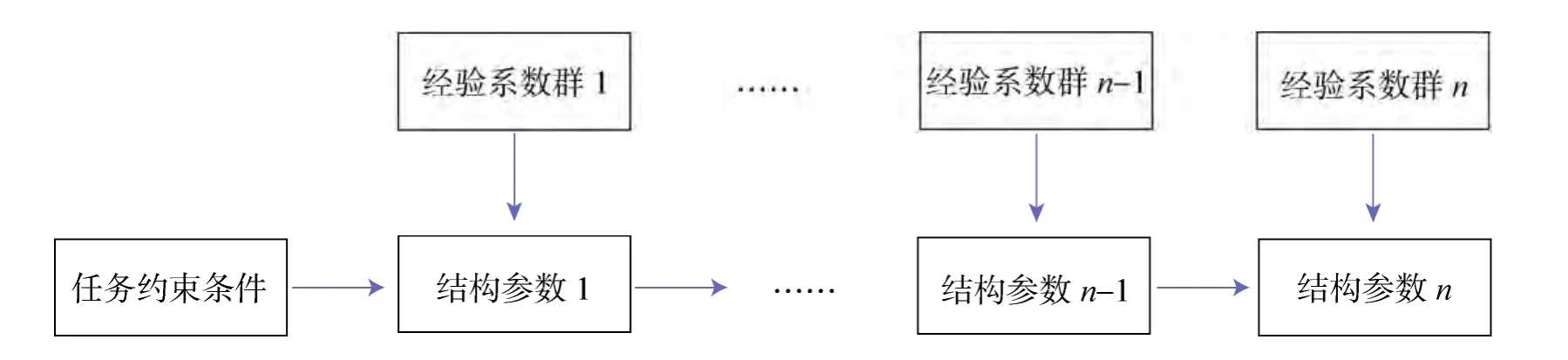
图1 结构参数构成Fig.1 Composition of structural parameters
可将环帆伞设计过程中涉及到的每一个结构参数记为

式中P为当前结构参数;B为输入因子;C为经验系数。输入因子B往往能够追溯到设计的初始输入,在设计框架内是不可调整的。因此,对设计结果进行的调整主要集中在C类参数上。C类参数可以是经验系数或经验公式,考虑到对经验公式进行灵敏度分析是不适宜的,这里特指经验系数。有些经验系数事实上在工程领域中是已经被广泛承认和使用的(如确定大气压强与海拔高度关系的模型系数等),有明确的选取规则,通常能通过查表、曲线或者线性插值的方式获得。这些参数虽然能够起到调节设计偏差的作用,但调整这些参数很可能会对设计过程的真实性、合理性造成影响;同时,后面的分析可以看到控制面积偏差与透气量偏差的可调参数较多,调整裕度较足,对这些选取规则明确的经验系数的调整并不必要。
对结构参数的灵敏度分析主要集中在用来确定当前结构参数、并且在选择的时候只给出了大致范围而并无明确选取规则的部分经验系数上,如确定伞衣幅数的伞衣幅系数syfN,记这一类参数为可变参数,见图2。
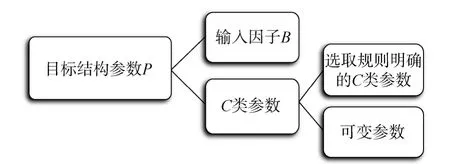
图2 结构参数构成分解Fig.2 Decomposition of structural parameter
通过分析整理环帆伞设计中各个结构参数的组成与继承关系,确定可变参数如下:
1)伞衣幅系数Nsyf。取值范围为2.5~3.0。
2)伞衣幅系数倍数关系。考虑到结构的对称性以及强度分布、安装、开伞完成度等需求,环帆伞幅数通常取为 4、6、8的倍数,视名义面积的大小而定。本文同时对Nsyf以及伞衣幅数倍数进行灵敏度分析。
3)绸布幅宽Hfk。为了保证充气外形与设计一致,小尺寸伞衣幅宽相应的也较小;同时,考虑到方便裁剪与节省布料,尽可能的按照2等分、3等分等进行等分裁剪。布料宽度为1m,实际应用中可裁为1m、0.5m、0.4m等,视名义直径大小而定。
4)环数Nhf。通过对环幅数系数与名义直径相乘的结果取整数获得。
5)三角幅高系数Nfg。通常取值范围为0.02~0.03。
6)缝宽Bhf。通常会根据透气量和强度设计的要求进行调整,比较灵活。考虑到实际型号中调整形式常以增大最后一环缝宽为其他缝宽2倍左右的形式出现[5],因此本文主要研究其它缝宽相同、最后一环缝宽为其它缝宽2倍的条件下,缝宽增大10%和减小10%对面积偏差和透气量偏差的影响。
7)设计阻力系数CD。根据名义尺寸由经验确定。
以上即是选取用于灵敏度分析的可变参数。需要注意的是,这里仅选取与设计面积偏差和透气量偏差相关的参数,其他参数如伞绳直径比等,尽管也属于可变参数的范围,但考虑到这些参数不会对设计的面积与透气量偏差造成影响、与本文研究的内容并无关系,因此不计在内。由于结构参数的调整会对环帆伞的性能产生影响[1,6],使初始设计阶段预估的环帆伞性能发生偏移,同时不恰当的尺寸配合甚至会造成环帆伞的失效[7-9],因此各个参数的调整均在较小范围内进行,尽可能的减小参数调整对环帆伞其他设计指标的影响。
2 分析方法
为了考察可变参数对设计偏差的灵敏度关系,参照环帆伞设计规范[4]编写了环帆伞设计程序。该程序以选定的可变参数作为变量,分析在不同的变量设置下依据设计流程完成一次伞衣幅结构设计时,面积偏差与透气量偏差随可变参数在常见环帆伞尺寸范围内的变化情况。考虑到研究以几何参数灵敏度分析为主,因此强度校核部分未包含在程序中。现定义面积偏差、透气量偏差如下

面积偏差和透气量偏差分别对应各自的灵敏度,如下

式中η为面积偏差灵敏度,表征参数值变化1个单位时,面积偏差值的变化情况。

式中ξ为透气量偏差灵敏度,表征参数值变化1个单位时,透气量偏差值的变化情况;伞衣名义面积由任务给定的阻力面积和设计选择的设计阻力系数决定,伞衣实际面积由设计得到的伞衣幅结构对每一个梯形伞衣片、梯形环缝和顶孔三角幅求和获得。
以某型号的可变参数取值为基础,调整1个可变参数并选定其它6个可变参数,利用环帆伞设计程序完成环帆伞几何结构的设计流程,获得不同可变参数值下、面积偏差和透气量偏差随伞衣尺寸分布的曲线,并分别对各个可变参数对面积偏差以及结构透气量偏差的灵敏度进行分析。这些试验除当前研究的可变参数不同外,其余各输入参数与经验系数均相同。各试验组的可变参数设置如表1所示:
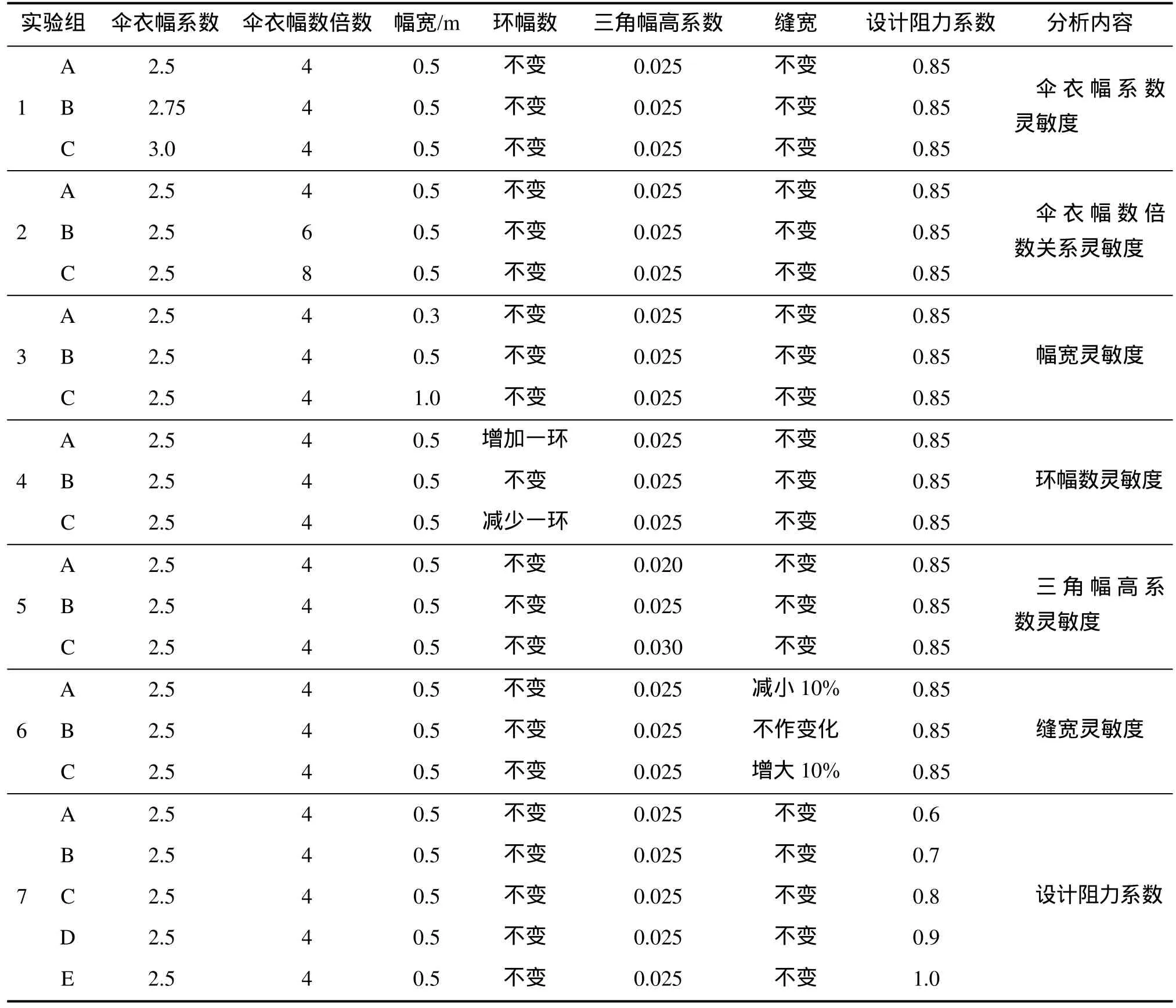
表1 试验可变参数设置Tab.1 Set up of alternative-parameter test
实际分析发现,有的可变参数灵敏度几乎不随伞衣尺寸改变、保持为一固定值,可采用定量的方式利用式(4)和式(5)进行分析;更多的情况则是可变参数灵敏度随伞衣尺寸变化,这时主要采用定性分析对其变化规律进行总结。
3 灵敏度分析
试验数据表明,不同可变参数组合下面积偏差与结构透气量偏差随尺寸变化的分布情况都是相似的,因此这里抽取了实验组1-A的结果对整体的偏差分布情况进行分析,见图3。

图3 典型偏差分布,取自试验组1-AFig.3 Typical distribution of area-deviation and porosity-deviation
考虑到偏差在0附近聚集时,不需做大的调整、设计的效果较好,因此有理由相信,至少从实际面积与透气量的角度上讲,实验组1-A对应的可变参数组合在设计名义直径为25m左右的环帆伞时将会获得较好的设计结果。
实际面积随名义直径变化的曲线呈阶梯状,从伞衣面积偏差图可以看出,这种阶梯状分布是由设计结果的振荡造成的。总的来看,试验结果呈现出局部振荡、整体规律的情况。反映到实际设计工作中,如果针对不同名义面积的环帆伞进行有限的几次设计活动,初次设计的结果可能有的是正偏差、有的是负偏差,看上去没有规律可言;但从统计学的意义上讲,结合图3可知在小尺寸设计时实际面积更可能出现的是负偏差、透气量为正偏差,也即是实际面积偏小、结构透气量偏大的情况,反之亦然。
随着名义直径的增大,面积偏差的分布逐渐由负偏差向正偏差的方向聚集,与之相反的是透气量偏差逐渐趋向于负偏差。在名义直径较小时,面积偏差的负偏差下限可达–20%、透气量偏差上限可达10%,表明在小尺寸条件下这种可变参数组合不可取。同时可以看到,伞衣面积与透气量上、下偏差振动的幅值随着名义尺寸的增大而减小,表明随着面积的增大,设计造成面积偏差与透气量偏差的不确定性逐渐减小。
3.1 伞衣幅系数Nsyf对伞衣面积偏差与结构透气量偏差的影响
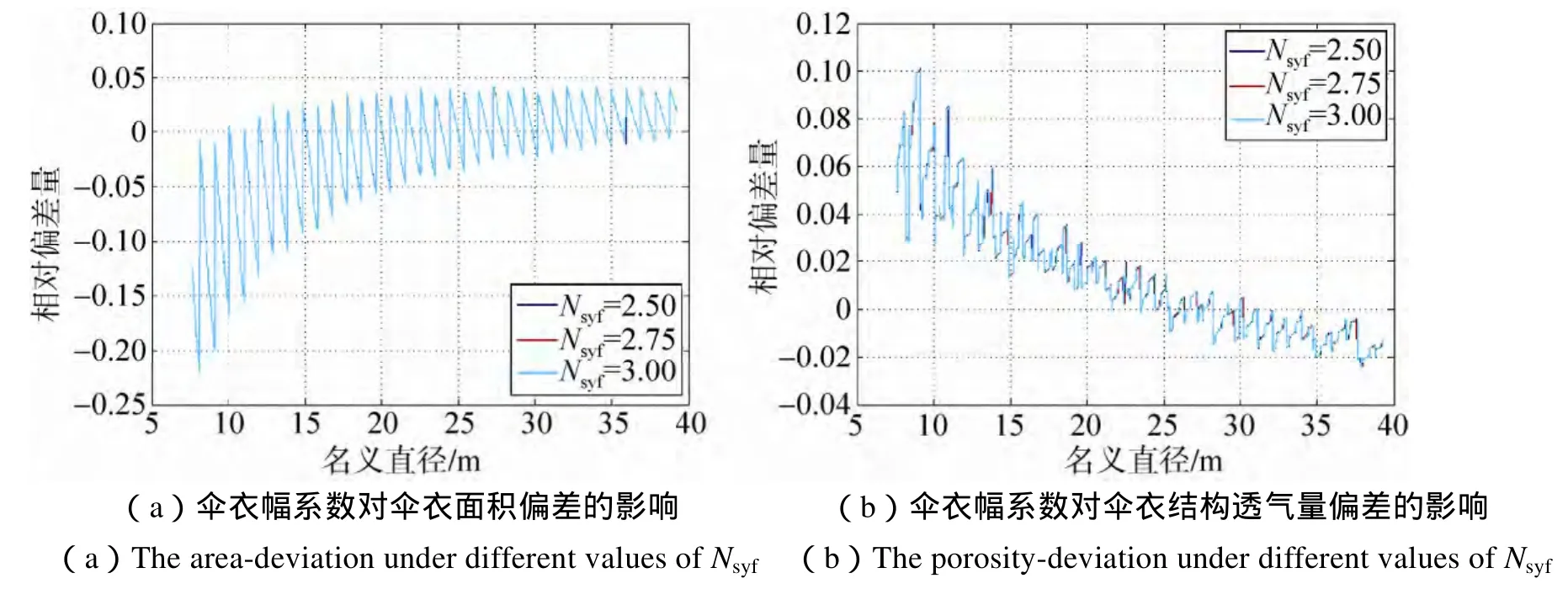
图4 伞衣幅系数对伞衣面积偏差与结构透气量偏差的影响Fig.4 The area-deviation and the porosity deviation under different Nsyf
根据设计规范, 伞 衣 幅数 =Nsyf×D0(D0为伞衣名义直径),并对结果进行取整数。图4为伞衣幅系数对伞衣面积偏差与结构透气量偏差的影响。由图可知,不同伞衣幅系数下的面积偏差曲线或透气量偏差曲线几乎重合,可以认为伞衣幅系数在 2.5~3.0的常用取用范围内,伞衣的面积偏差与透气量偏差几乎不发生变化。也即是说,设计的伞衣面积偏差与透气量偏差对伞衣幅系数不敏感,该系数在实际设计中可作为强度、工艺等其他指标的调节参数而不对伞衣面积与结构透气性造成影响。
3.2 伞衣幅取用倍数对伞衣面积偏差与结构透气量偏差的影响
不同伞衣幅数取用倍数的试验结果如图5。事实上,针对同一名义直径选用不同伞衣幅倍数得到的伞衣幅数之间差别不会大于8幅,仅相当于对伞衣幅数起到微调的作用。由前面面积偏差与透气量偏差对伞衣幅数不敏感的结论可以推断,这2个偏差对伞衣幅数的取用倍数也是不敏感的。试验的结果验证了这一点,面积偏差与透气量偏差几乎不随伞衣幅取用倍数的变化而改变。

图5 伞衣幅倍数对伞衣面积偏差与结构透气量偏差的影响Fig.5 The area-deviation and porosity-deviation under different times of Nsyf
3.3 绸布幅宽Hfk对伞衣面积偏差与结构透气量偏差的影响
不同幅宽的试验结果如图6、图7所示。试验表明,面积偏差的上偏差限对伞衣幅宽不敏感,随幅宽改变的变化较小;下偏差限在小尺寸时对伞衣幅宽较为敏感。同时,随着幅宽的减小,面积偏差趋向于正偏差,透气量偏差趋向于负偏差。环帆伞依据理论几何外形进行设计,幅宽越小,同样尺寸下每幅的环幅与帆幅数越多,设计得到的伞衣几何外形也就越接近于理论几何外形。因此,随着幅宽的减小,可推测面积误差曲线的振荡幅值会逐渐减小。图6中幅宽为0.3m的曲线当名义尺寸较大时聚集在0值附近振动的情况验证了这一点。
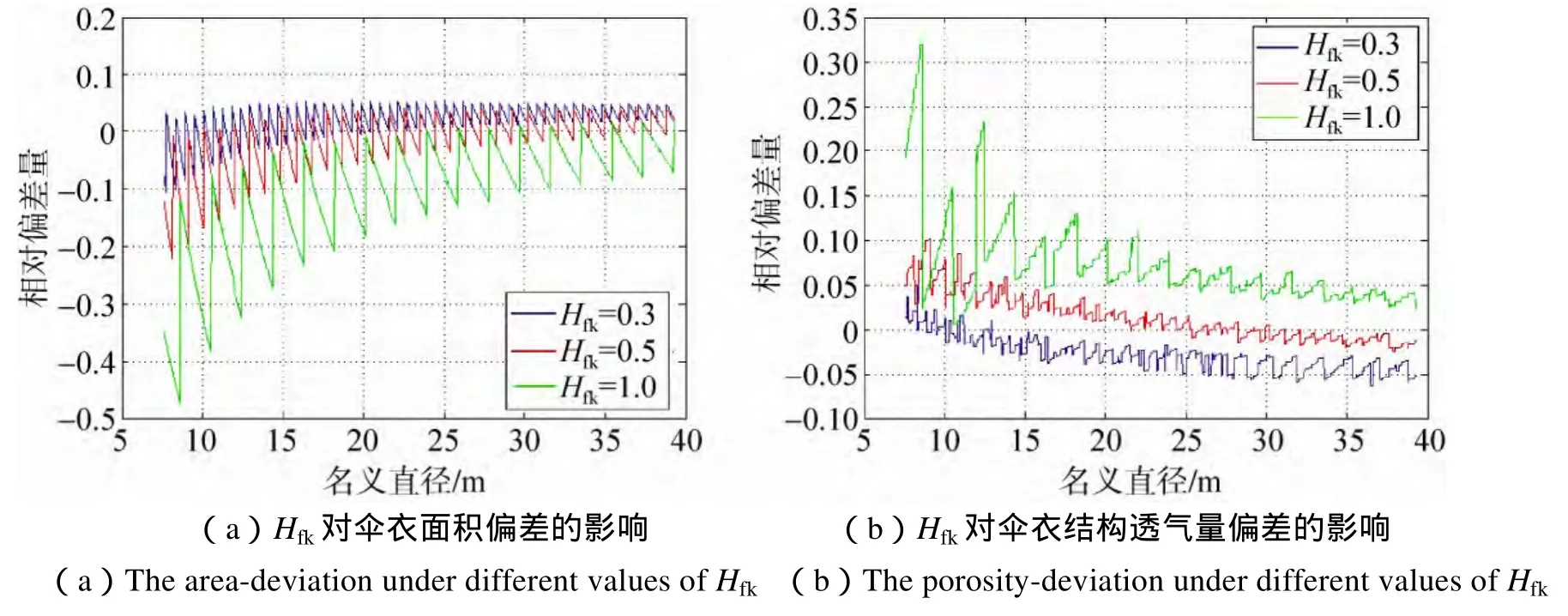
图6 幅宽对伞衣面积偏差与结构透气量偏差的影响Fig.6 The area-deviation and the porosity-deviation under different values of Hfk
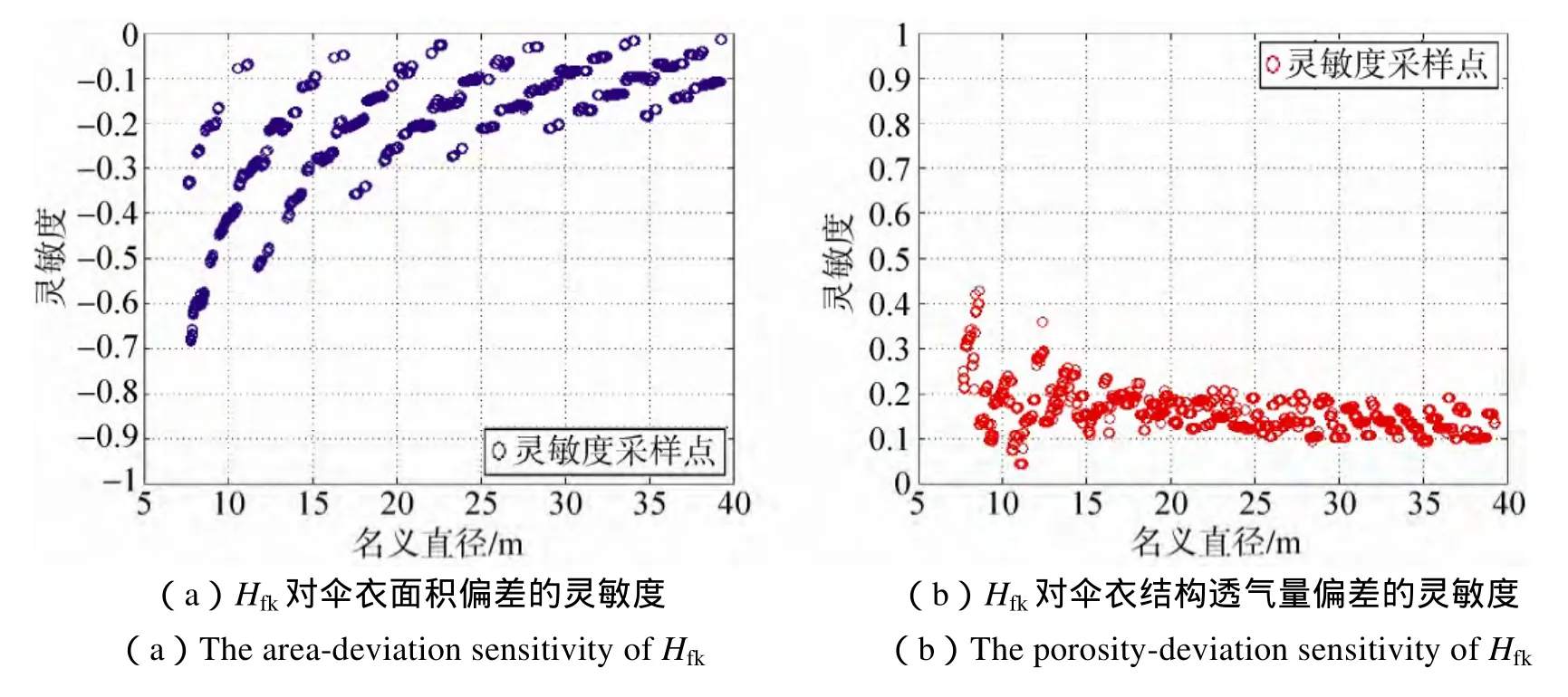
图7 幅宽对伞衣面积偏差与结构透气量偏差的灵敏度Fig.7 The area-deviation sensitivity and the porosity-deviation sensitivity of Hfk
灵敏度方面,无论是面积偏差灵敏度还是透气量偏差灵敏度也都遵循小直径较分散,大直径集中收敛的规律。总的来看,增加幅宽为面积偏差提供负修正量、为透气量偏差提供正修正量;然而,小直径的伞型由于幅宽灵敏度较发散,用幅宽校正不易控制校正结果;而在对大尺寸伞型初次设计结果进行校正时,增大0.1m的幅宽可获得约–1%左右的面积偏差修正量和1.5%左右的透气量偏差修正量。
3.4 环数Nhf对伞衣面积偏差与结构透气量偏差的影响
环数变化的试验结果如图8、图9。对环幅数灵敏度的考察通过人为地在原有设计规范上增加或者减少一环的方式进行,在这一过程中每伞衣幅的总幅高保持不变。由图9可知,相较于幅宽,环幅数对面积偏差灵敏度与透气量偏差灵敏度的收敛性较好,更容易估算利用该参数对2个偏差调整的效果。
总的来看,环幅数对面积偏差为负修正量,对透气量偏差在大部分尺寸范围内为正修正量;在小尺寸条件下,环幅数对2个偏差的灵敏度较强,面积偏差灵敏度可达–0.02,透气量偏差灵敏度可达+0.08;尺寸较大时,偏差灵敏度进一步收敛,面积偏差灵敏度在–0.004左右,透气量偏差在±0.01的范围内。也即是说,在名义尺寸较大时,如果保持总幅高不变而增加一环(相应的帆幅减少一幅),将会带来实际面积约0.4%的负增量;而对透气量的修正量则分布在±1%之间,既有增大透气量、也有减小透气量的可能,因而不易估算修正结果,修正效果并不理想。
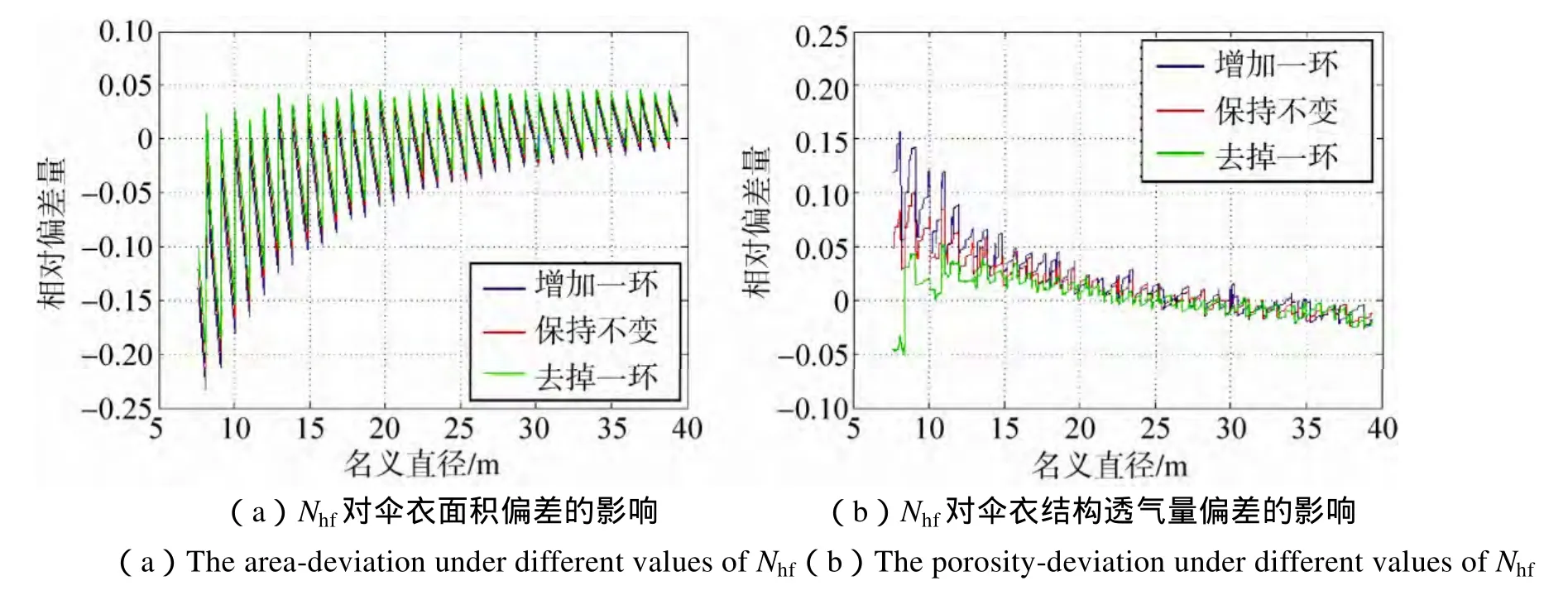
图8 环幅数对伞衣面积偏差与结构透气量偏差的影响Fig.8 The area-deviation and the porosity-deviation under different values of Nhf
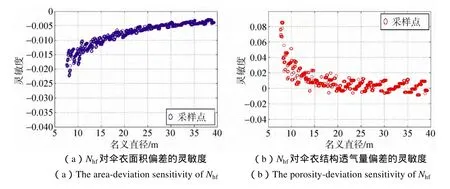
图9 环幅数对伞衣面积偏差与结构透气量偏差的灵敏度Fig.9 The area-deviation sensitivity and the porosity-deviation sensitivity of Nhf
3.5 三角幅高系数Nfg对伞衣面积偏差与结构透气量偏差的影响
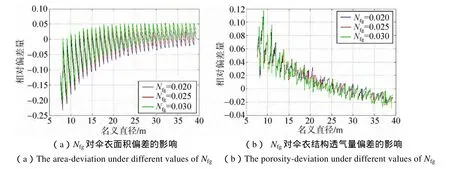
图10 三角幅高系数对伞衣面积偏差与结构透气量偏差的影响Fig.10 The area-deviation and the porosity-deviation under different values of Nfg
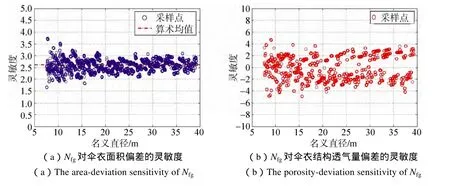
图11 三角幅高系数对伞衣面积偏差与结构透气量偏差的灵敏度Fig.11 The area-deviation sensitivity and the porosity-deviation sensitivity of Nfg
不同三角幅高系数的试验结果如图10、图11。将幅高系数分别取作0.025 0、0.027 5和0.030 0进行3组试验。由图11可知,三角幅高系数对面积偏差的灵敏度随着面积的增大逐渐集中于2.6±0.5的范围内,对透气量偏差的灵敏度则散布在±4的范围内。考虑三角幅高系数取值范围为0.025 0到0.030 0,取值较小、调整的幅度相应较小。也即是说,通过调整三角幅高系数 0.001可获得对面积偏差约 0.2%到 0.3%左右的稳定修正量,对透气量偏差的修正量在±0.4%的范围内。与环幅数类似,由于调整的结果在正负偏差范围内都有较为均等的分布,因而三角幅高对于透气量而言并不是一个好的修正参数。
近年来,旅游地是环境污染的重灾区。一些污染物不容易消解,会对自然环境造成巨大的影响[3]。旅游地产品应尽量使用可再生资源。杜绝景区不文明消费,营造一个绿色消费的旅游环境。在旅游消费中,应注重精神文化消费和适度消费,建立健全景区绿色消费制度。
3.6 设计阻力系数CD对伞衣面积偏差与结构透气量偏差的影响
令CD在0.6~1.0的区间内等分取值共进行5次试验。在环帆伞设计过程中,CD主要用于确定给定阻力面积下的名义面积,如式(6)所示

式中 [CA]0为阻力面积、由任务指标给定;A0为名义面积。
就结构设计而言,CD的作用仅在于为不同的任务指标提供相应的名义尺寸,并不影响设计产生的面积偏差和透气量偏差随名义尺寸变化的曲线;也即只有CD不同、其余输入参数和可变参数均相同的两次环帆伞设计,设计的面积偏差与透气量偏差分别对应的是同样的面积偏差曲线与透气量偏差曲线、只是在曲线上的对应点不同而已。试验结果证实了这一点(图12),不同CD的曲线除了由名义尺寸范围变化而导致的绘图区间差异之外完全重合。对于某次设计活动而言,设计阻力系数只是影响该次设计所对应的名义尺寸大小,也即是在曲线上的取点位置。

图12 设计阻力系数对伞衣面积偏差与结构透气量偏差的影响Fig.12 The area-deviation and the porosity-deviation under different values of CD
3.7 缝宽Bhf调整百分比对伞衣面积偏差与结构透气量偏差的影响
在原有设计流程的基础上减小和增大10%所有缝宽,进行3次试验。由图13与图14可知,缝宽对面积偏差的影响较小,对透气量偏差影响较大,并且在增大缝宽时,实际面积与结构透气量都同时增大。在小尺寸时,缝宽对面积偏差的灵敏度在0.06到0.12之间变动,也即是说增大10%的缝宽会增加0.6%到1.2%左右的面积;而在较大尺寸时,增大10%的缝宽会增大0.6%到0.8%左右的面积,浮动区间较小,能够实现较精确的调节。同时,缝宽在小尺寸与大尺寸环帆伞设计中因为对透气量的灵敏度较高且浮动较小,能够实现对透气量较为快速与精确地调节,10%的缝宽增量可换来9%左右的透气量增量。

图13 缝宽对伞衣面积偏差与结构透气量偏差的影响Fig.13 The area-deviation and the porosity-deviation under different values of Bhf
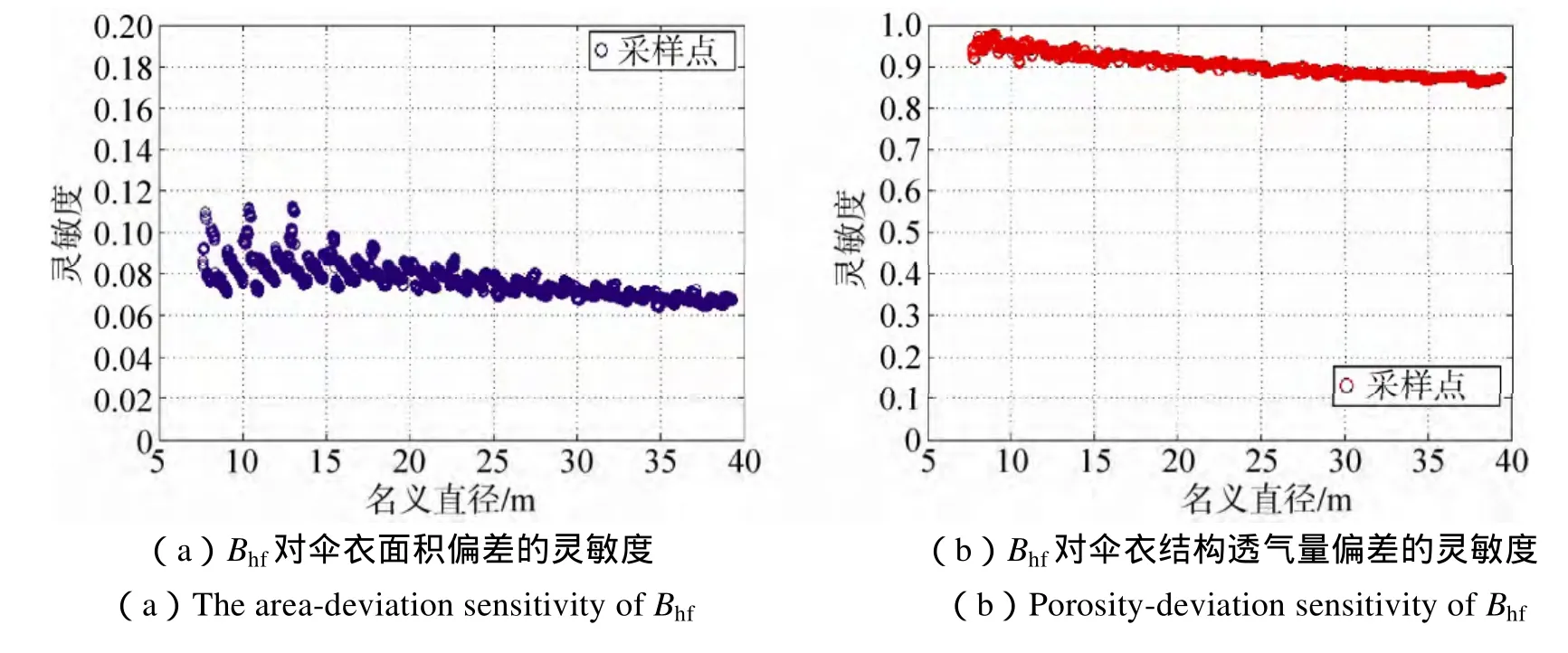
图14 缝宽对伞衣面积偏差与结构透气量偏差的灵敏度Fig.14 The area-deviation sensitivity and the porosity-deviation sensitivity of Bhf
4 结束语
通过对不同可变参数取值下的环帆伞设计结果进行分析和比较,得到关于环帆伞设计偏差的几点结论如下:
1) 设计获得的伞衣实际面积随设计名义尺寸的变化关系是一条振荡并在x轴远端收敛的曲线。也即,尽管随着尺寸的增大,设计结果的离散性会逐渐减弱,但在局部范围、特别是常规环帆伞所取用的尺寸范围内,设计结果的离散性还是很强。
2)对设计产生的面积偏差可以通过增减环幅数、调整三角幅高和环缝宽度获得较好的修正结果,这3个可变参数对面积偏差的灵敏度相似,都在2%到0.2%的范围内。
3)对设计产生的透气量偏差可通过调整幅宽、缝宽以及增减环幅数获得较好的修正,其中幅宽和环幅数的灵敏度较低,可作为细调使用;缝宽的灵敏度较高,可作为粗调使用。
以上结论可作为设计人员对设计结果进行调整的参考。然而,需要注意的是,在设计尺寸较小的环帆伞时设计结果的离散性较强,面积偏差与透气量的偏差分布区间较大,规律性较弱;各个可变参数的灵敏度在小尺寸设计时离散性也都较强,难以实现规范、快速地对设计结果进行修正。同时,考虑到可能的参数组合较多,而本文只是选取了一种较为常见的参数组合作为研究基础,因此这些结论在整个环帆伞设计所覆盖的参数组合范围内是否具有稳定性,需要通过进一步的研究加以明确和细化。
(
)
[1] Edgar G E.Ringsail Parachute Design[R].AFFDL-TR-72-3, California: Northrop Corporation, 1972.
[2] Theo W K.Parachute Recovery Systems Design Manual[M].California: Para Publishing, 1992.
[3] 李健, 唐明章.“神州八号”飞船主伞的改进设计与试验[J].航天返回与遥感, 2011, 32(6): 26-32.
LI Jian, TANG Mingzhang.Improvement and Tests of the SHENZHOU-8 Main Parachute[J].Spacecraft Recovery & Remote Sensing.2011, 32(6): 26-32.(in Chinese)
[4] 王利荣.降落伞设计导论[M].北京: 宇航出版社, 1997.
WANG Lirong.An Introduction to Parachute Design[M].Beijing: China Astronautic Publishing House, 1997.(in Chinese)
[5] 李健, 王立武.伞顶控制带的设计、试验与应用[J].航天返回与遥感, 2010, 31(2): 10-15.
LI Jian, WANG Liwu.Design, Test and Application of the Vent Control Bridle[J].Spacecraft Recovery & Remote Sensing,2010, 31(2): 10-15.(in Chinese)
[6] 连亮, 张红英, 李方, 等.结构参数对火星探测用伞开伞性能的影响[J].航天返回与遥感, 2012, 33(6): 24-29.
LIAN Liang, ZHANG Hongying, LI Fang, et al.Influence of Structure Parameters on inflation Performance of Parachute Used for Mars Exploration[J].Spacecraft Recovery & Remote Sensing.2012, 33(6): 24-29.(in Chinese)
[7] 夏刚, 程文科, 秦子增.航天器回收中几种主伞失效案例介绍[J].航天返回与遥感, 2002, 23(4): 4-8.
XIA Gang, CHENG Wenke, QIN Zizeng.Case Study of Main Parachute Malfunction in Aerospace Recovery[J].Spacecraft Recovery & Remote Sensing, 2002, 23(4): 4-8.(in Chinese)
[8] West R B.Apollo Experience Report: Earth Landing System[R].NASA TN D-7437, 1973.
[9] Runkle R.STS-3 Main Parachute Failure[R].NASA TM-82490, 1982.
