改善返回舱气动稳定特性数值计算研究

陈冰雁 詹慧玲 周伟江 刘周

（中国航天空气动力技术研究院，北京 100074）

0 引言

和第一宇宙速度载人再入飞行相比，以第二宇宙速度再入飞行所面临的难度更大，对返回器（一般采用轴对称钝头体外形）气动特性的要求更高。近地轨道载人飞船返回舱（如“联盟号”）能够成功实现第一宇宙速度的载人再入飞行，但是对于月球返回或星际返回的载人任务，这种返回舱气动外形由于升阻比比较低，难以满足第二宇宙速度载人再入飞行对最大过载限制和纵横向机动能力的要求。美国实施“阿波罗”计划时曾论证过，载人登月任务对返回舱升阻比的最低要求是0.25，设计升阻比在0.3～0.4之间[1]。“联盟号”返回舱的升阻比不能满足这样的设计要求。“阿波罗”飞船返回舱虽然升阻比比较高，但是存在非单点稳定的问题，即在0°～ –180°攻角范围内存在2个或2个以上的静稳定配平点。假如返回器在再入过程中以非设计配平攻角飞行，那么热防护系统不能提供足够保护，其后果将是灾难性的。“阿波罗”采用了一套备用的反作用力控制系统（Reaction Control System）来确保在主控制系统失效的情况下仍能够控制返回器的飞行姿态。但是在控制系统全部失效的情形下，返回器的飞行安全很难得到保证。而对于单点稳定的返回器外形，如“联盟号”，即使控制系统失效，返回器在飞行姿态偏离设计点的情况下也能够自动回到唯一的静稳定配平设计点。因此，单点稳定特性是关乎返回器飞行安全的一项关键气动性能。[2-3]

詹慧玲等针对“联盟号”、“阿波罗”等典型返回器外形开展了气动特性的对比和改进研究[4]，本文在此研究基础上给出了一种升阻比能够满足第二宇宙速度再入需求的返回器基本外形，通过计算流体力学（Computational Fluid Dynamics, CFD）数值模拟对其气动稳定特性进行了分析，分析结果表明基本外形在高超声速和亚声速下均存在第二静稳定配平点。为此，尝试在基本外形的基础上通过安装稳定耳片和改变尾部外形等改进设计来改善基本外形的气动稳定特性以消除第二静稳定配平点。对改进外形气动稳定特性的分析结果表明，这些改进设计对于改善基本外形的单点稳定特性是有效的，但改善的效率有所不同，仅有一种外形消除了第二静稳定配平点，实现了单点稳定。通过对返回器绕流流场特性的详细剖析，外形改进设计对返回器稳定特性的影响机理得到了解释。

1 计算方法

1.1 几何外形

本文所研究的返回器外形如图1所示，其中B0为只有舱体的基本外形，B1～B3是为了改善基本外形气动稳定性的改进外形。B1在基本外形的后体迎风面设计了一对稳定耳片；B2则把基本外形的底部凸台高度增加了一倍，并设计成外扩锥体，外扩锥角为9°；B3同样是对底部凸台进行了改进设计，凸台高度与B2外形一样，但上半部设计成平台形状，下半部设计成柱体形状。

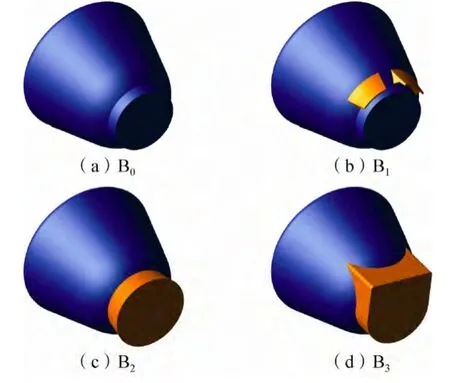
图1 返回器外形Fig.1 Capsule configurations

图2给出了基本外形B0的几何尺寸定义，图中dm为舱体最大截面直径，RN为球冠半径，RC为肩部半径，θ为后体倒锥角。基本外形的后体倒锥角θ设计值为 16°，球冠钝度RN/dm=1.2，相对肩部半径RC/dm=0.04。这3个主要几何参数基本上确定了这种返回器外形的升阻比，事实上基本外形几何参数的设计值主要是根据升阻比要求来确定的[4]。

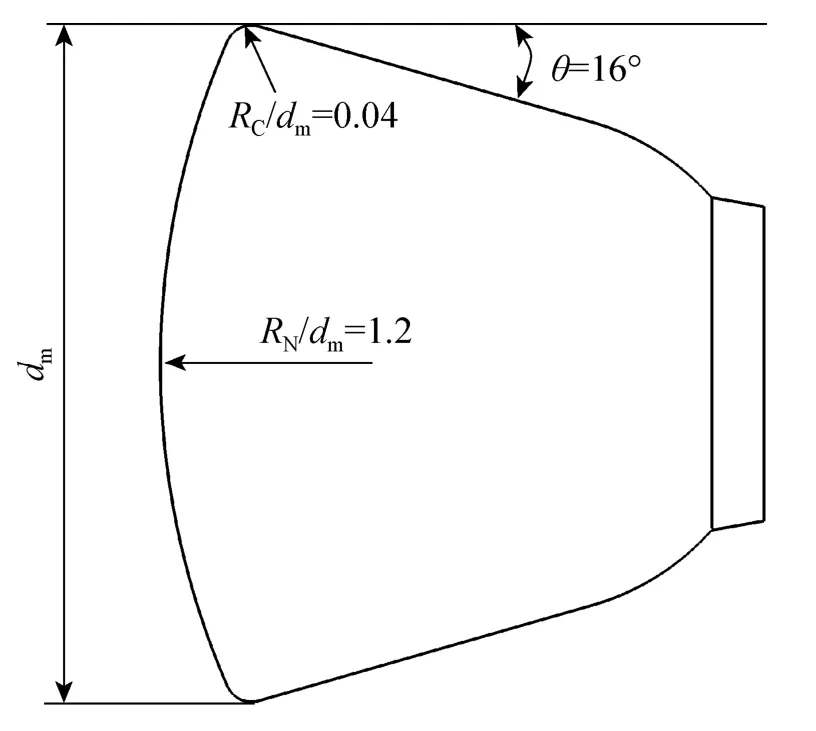
图2 基本外形几何尺寸Fig.2 Geometrical definition of the basic configuration.

1.2 分析工具

本文对返回器气动特性的预测与分析是通过 CFD数值计算来完成的，所采用的CFD工具是由中国航天空气动力技术研究院自主研发的CFD软件平台——CACFD。CACFD软件平台包括1个能够实现贴体粘性笛卡尔网格[3]自动生成的网格生成器以及1个基于Roe[5]格式的纳维–斯托克斯（Navier-Stokes，N-S）方程解算器，解算器集成了一方程湍流模型[6]（Spalart-Allmaras）以及多种两方程湍流模型（如 Wilcox k-omega 1998[6]、Wilcox k-omega 2006[7]、Menter SST k-omega[8]）应用于湍流的模拟。

图3给出了采用CACFD对典型返回器外形生成的笛卡尔网格以及计算得到的流场。图3（a）显示了通过笛卡尔网格生成器获得的典型返回器外形表面网格和对称面的空间网格，图3（b）显示了通过流场解算器获得的典型返回器外形表面压力分布云图以及对称面的流线（计算状态为Ma=10，攻角α=–25°）。

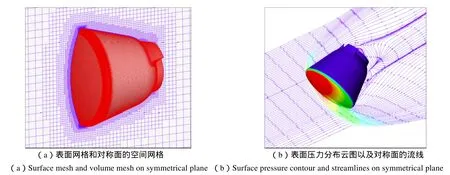
图3 采用CACFD获得的典型返回器笛卡尔网格和计算流场Fig.3 Cartesian mesh and flowfield of a typical capsule obtained by CACFD

1.3 坐标系定义

本文对气动力与力矩系数计算结果的分析均采用如图4所示的弹体坐标系。气动参考面积为返回器迎风最大横截面积，参考长度为返回器迎风最大截面直径，力矩参考点为质心位置。x轴沿舱体向前，从后视图看，y轴朝上，z轴朝右。攻角为0°时大头朝前。图中，CA、CN、CZ、CMx、CMy和CMz分别为轴向力系数、法向力系数、侧向力系数、滚转力矩系数、偏航力矩系数和俯仰力矩系数；Xcg、Ycg和Zcg为量纲一的质心系数；α和β分别为攻角和侧滑角；V∞为来流速度，Vx、Vy、Vz分别为来流速度在x、y、z这3个方向上的分量。

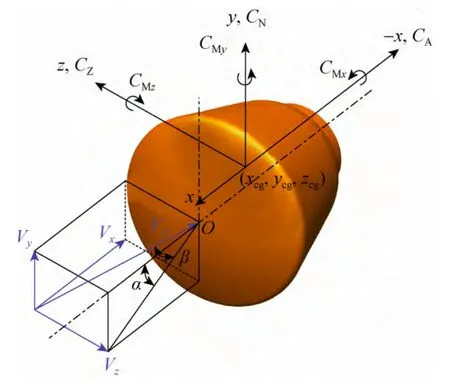
图4 弹体坐标系定义Fig.4 Definition of body coordinate system

2 计算结果与分析

2.1 基本外形的气动特性

通过CFD数值计算，获得了基本外形在Ma=0.6、10，α= 0 ～ –180°时的气动特性，如图5所示。图5（a）给出了升阻比L/D随α的变化曲线，图5（b）则给出了CMz随α的变化曲线。

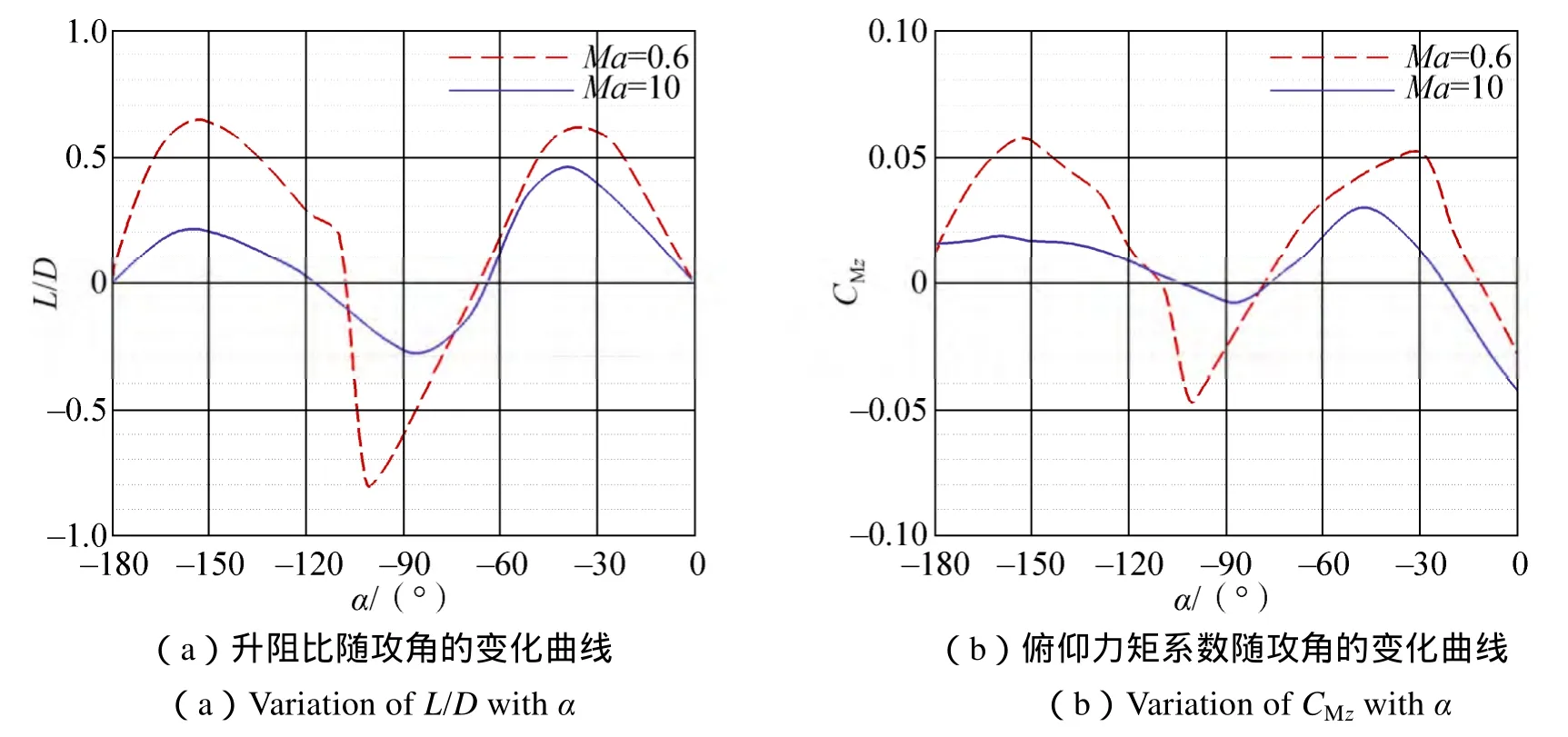
图5 基本外形气动特性的CFD计算结果Fig.5 Aerodynamic characteristics of the basic configuration obtained by CFD calculations

图中数据是在质心位置设定为（Xcg=0.36，Ycg=0.031）的条件下得到的，在此质心位置下，返回器在Ma=10时配平攻角αT为–23°，对应的配平升阻比可达 0.31。这一配平升阻比已略高于“阿波罗”的配平升阻比（0.30），能够满足第二宇宙速度载人再入飞行的升阻比要求。

但是从俯仰力矩系数随攻角变化曲线可以看到，无论是在高超声速（Ma=10）还是亚声速（Ma=0.6），基本外形在–100°～–110°攻角附近均存在第二静稳定配平点。假如返回器在再入过程中以第二静稳定配平攻角飞行，这种情况出现在高超声速时返回器会被烧毁，如果出现在亚声速时可能会影响着陆减速伞的成功展开，同样会威胁到返回器内乘员的生命安全。因此在设计返回器气动外形时应尽可能消除第二静稳定配平点。

2.2 质心位置对单点稳定特性的影响

返回器外形的气动稳定特性是随质心位置的变化而改变的，假如质心位置能够足够靠近防热大头，那么第二静稳定配平点能够被消除。图6给出不同质心位置下，俯仰力矩系数随攻角变化曲线的对比。对于Ma=10和 0.6，图中均给出了 3个不同质心位置下的俯仰力矩曲线。其中质心位置是在Ma=10、αT=–23°的配平线上变化的，也就是说，质心位置的变化不改变Ma=10时的配平攻角。从图中不难看出质心位置变化对单点稳定特性的基本影响规律：随着质心位置的前移（Xcg减小），单点稳定特性逐渐改善并最终实现单点稳定。

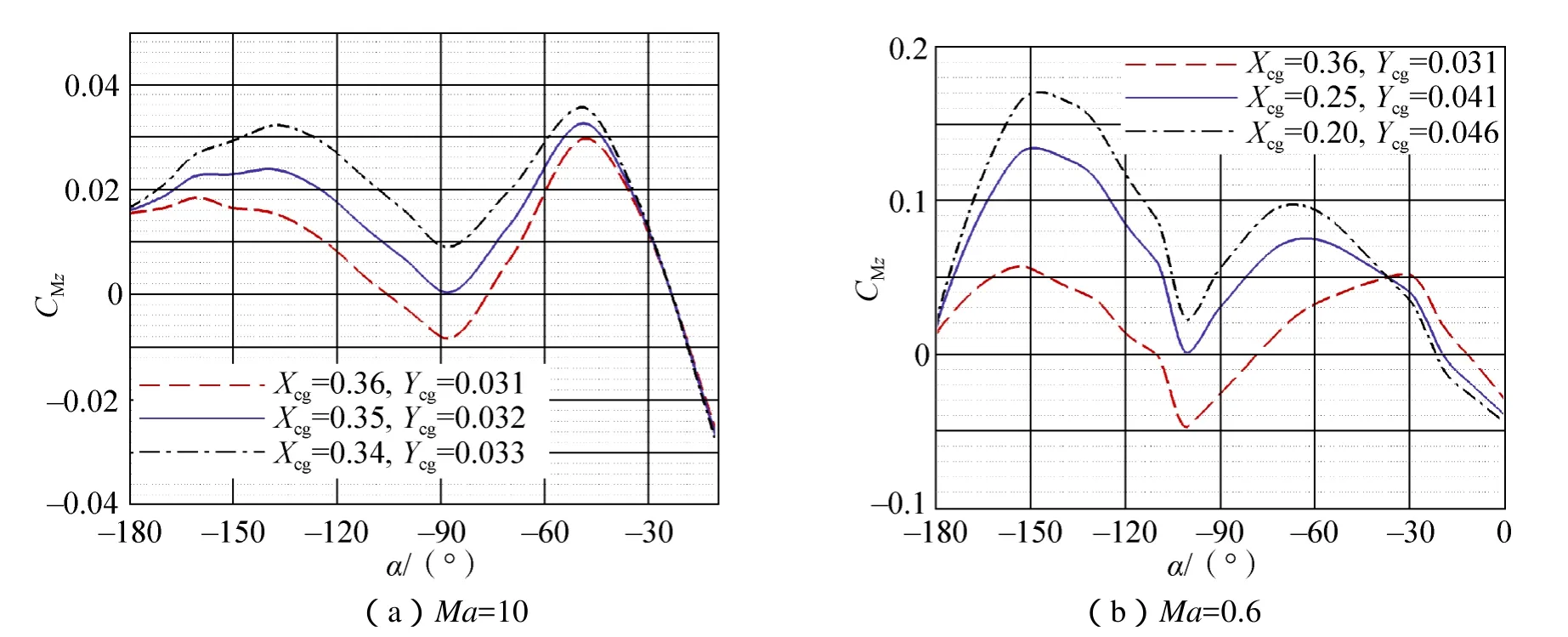
图6 质心位置对基本外形单点稳定特性的影响Fig.6 Effects of center of gravity location on the stability characteristics of the basic configuration

图6中的蓝实线是在临界质心位置下得到的俯仰力矩系数曲线，临界质心位置是指返回器外形从非单点稳定转变为单点稳定时的质心位置。在Ma=10时的临界质心位置为（Xcg=0.35,Ycg=0.032），和初始设计值相差不太远。但Ma=0.6时的临界质心位置则变成（Xcg=0.25,Ycg=0.041），事实上，这样的质心位置在工程设计中是极难达到的。换言之，通过改变质心位置来消除基本外形的第二静稳定配平点在高超声速时或许可行，但在亚声速下则是不现实的。只能通过对气动外形的改进设计来改善其单点稳定特性。

2.3 改进外形的稳定特性分析

为了消除基本外形的第二静稳定配平点，尤其是在亚声速下，本文提出了3种改进外形（图1中的B1～B3）。同样采用CFD数值方法对这些改进外形在Ma=0.6时的稳定特性进行了预测计算，并与基本外形 B0进行了比较。

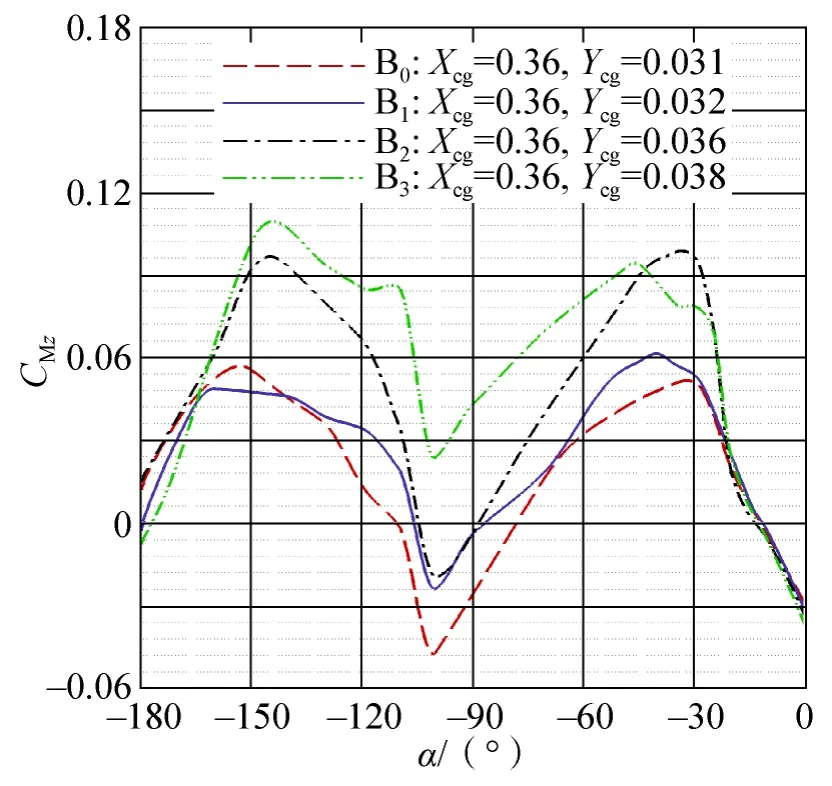
图7 不同外形单点稳定特性的比较Fig.7 Comparison of stability characteristics for different configurations

图7给出了Ma=0.6时，这4种外形的俯仰力矩系数随攻角变化曲线的比较。所有外形的x方向的质心系数均设定为Xcg=0.36，y方向的质心系数Ycg则通过Ma=10时的配平特性来确定，以保证所有外形在Ma=10时的αT=–23°。

由图可见，这3种改进外形设计均能够在一定程度上改善基本外形的稳定特性。B1和B2虽然没有消除第二静稳定配平点，但是非单点稳定的程度和基本外形相比有所减弱（俯仰力矩系数最小值上移）。而B3外形则完全实现了单点稳定，单点稳定特性相对于基本外形得到了极大的改善。

2.4 改善稳定特性的机理分析

从图 7中可以看到Ma=0.6时，α=–100°是俯仰力矩在α=–120°～–90°附近的局部最低点。如果俯仰力矩系数在该点为正，则返回器外形是单点稳定的，如 B3外形；相反，如果俯仰力矩系数在该点为负，那么将会出现第二静稳定配平点。

为了揭示外形改进设计对单点稳定特性的影响机理，根据数值模拟结果对各返回器外形在这一状态点的流场特性进行了剖析。4种返回器外形在关键状态点（Ma=0.6，α=–100°）的表面压力分布云图和对称面的流线走向如图8所示。图中的压力云图以量纲为一的压力参数值p/γp∞来绘制，其中p为计算得到的压力，p∞为来流压力，γ为比热比。从图中可以看到，不同外形的绕流流场结构在迎风面是基本相似的；但在背风面，不同外形之间流场结构存在比较大的差异。这些差异有可能对返回器外形的稳定特性产生比较大的影响。

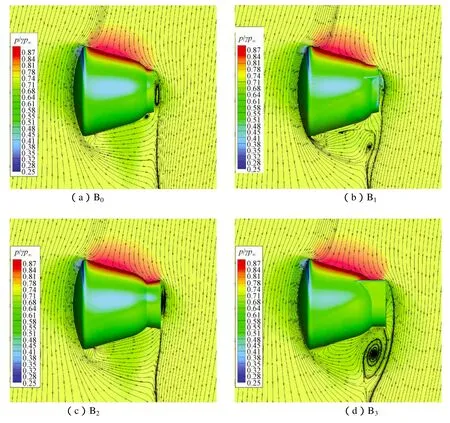
图8 在关键状态点（Ma=0.6，α=–100°）时，4种返回器绕流流场特性的比较Fig.8 Comparison of flow field around capsules under critical condition（Ma=0.6，α=–100°）

从各外形沿对称线上表面压力分布的比较中（如图9所示）可以证实以上推测。图9中纵坐标为量纲一压力p/p∞，横坐标为对称线上的x坐标与返回器最大截面直径dm之比。在迎风面，各外形的压力分布在绝大部分区域是基本一致的，只是在尾部出现差异，这主要是由于不同外形之间尾部几何外形的差异所造成的。很显然，B2和B3外形在尾部的压力和基本外形B0相比要高。

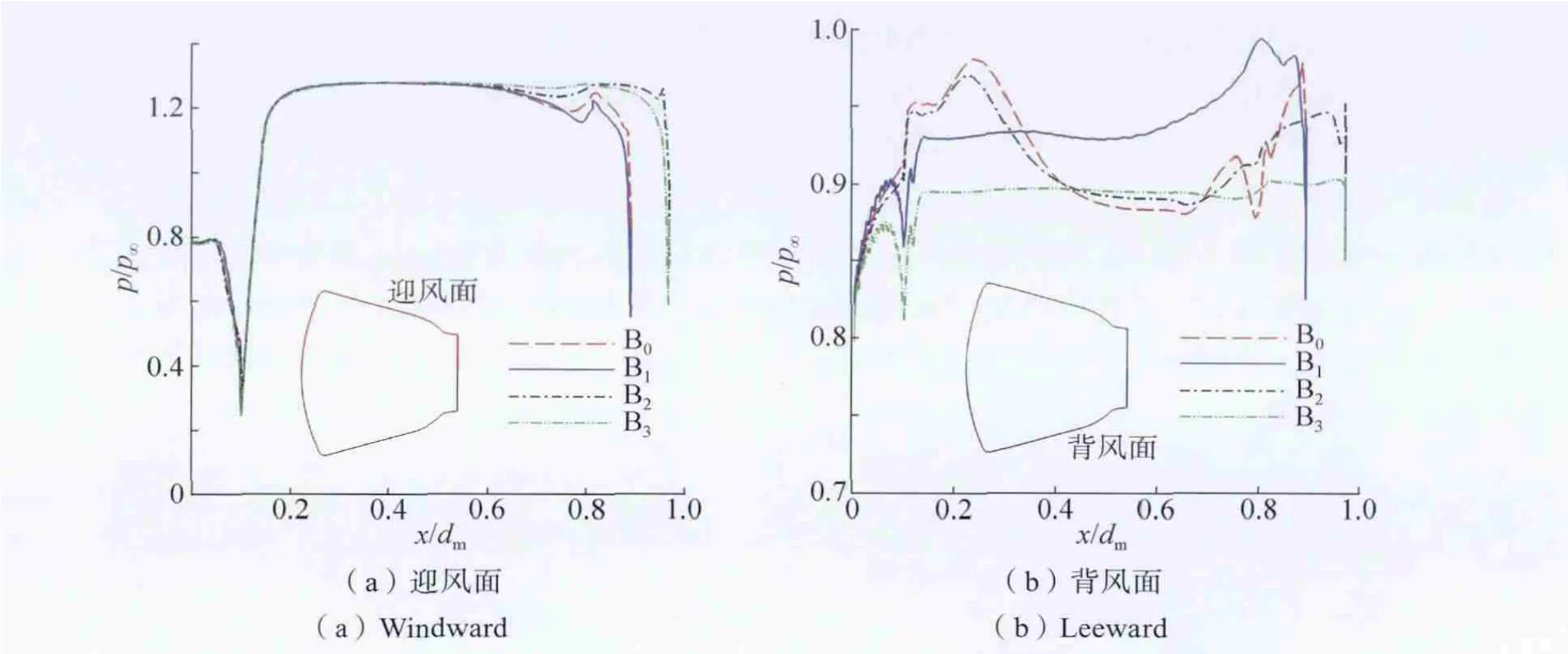
图9 在关键状态点（Ma=0.6，α=–100°）4种返回器沿对称线表面压力分布比较Fig.9 Comparison of pressure distribution along symmetrical line on capsule surface under critical condition（Ma=0.6，α=–100°）

从图中可以看出，在背风面，不同外形的压力分布则完全不一样，即使在几何外形完全相同的前面部分也是如此。值得注意的是，B3外形背风面的压力明显低于其他外形。这一现象与 B3外形的单点稳定性是有联系的。

压力分布的差异对返回器外形气动稳定性的影响机理，见图10示意。在图中所示状态下，使返回器顺时针转的俯仰力矩是起稳定作用的，因为它使返回器回到大头朝前的姿态；反过来，使返回器逆时针转的俯仰力矩则是使返回器不稳定的，因为它是返回器走向小头朝前的姿态。作用在后锥体迎风面和背风面的力对于俯仰力矩的贡献是比较小的，因为力臂很短。作用在球冠大头迎风面的力对于所有外形来说都是一样的，因为压力分布都一样。因此，对稳定力矩和不稳定力矩起主要作用的是作用在尾部（包括耳片）的力以及作用在球冠大头背风面的力。

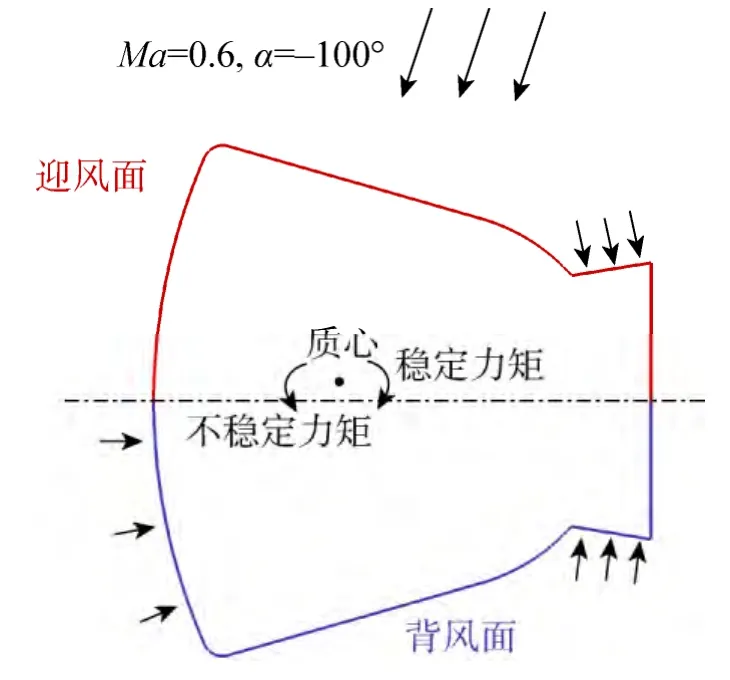
图10 压力分布对返回器稳定特性的影响机理Fig.10 Mechanism of effect of pressure distribution on capsule stability characteristics

作用在尾部迎风面的力产生稳定力矩，而作用在尾部以及球冠大头背风面的力则产生不稳定力矩。因此，B1的耳片以及 B2和B3的长尾部均产生直接的稳定力矩来改善返回器的稳定性；除此之外，B3由于在背风面的压力比较低，作用在尾部以及球冠大头背风面的力比较小，从而减小了不稳定力矩，这一影响因素同样能够改善返回器的稳定性。因此，B3是唯一具有单点稳定的特性。

3 结束语

本文通过数值计算对4种返回器外形的气动特性进行了分析，其中基本外形的单点稳定特性不能满足设计要求，但通过安装稳定耳片或者改变尾部外形等改进设计，基本外形的单点稳定特性能够得到改善，并最终实现单点稳定。通过对流场特性的详细剖析，认识了外形改进设计对返回器气动稳定特性的影响机理。分析结果表明，作用在耳片和增长尾部上的力能够产生稳定力矩来改善返回器的稳定性；此外，外形改进设计对流场结构的改变也是改善返回器稳定性的一个重要因素。要得到单点稳定的外形，这2种改善稳定性的机理都必须得到充分的利用。

（

）

[1] Jon C.Harpold, Minimum Lift-to-drag Ratio Requirement for the Lunar Mission[R].NASA-TM-X-69752, 1967.

[2] ESAS Team.NASA’s Exploration Systems Architecture Study Final Report[R].NASA-TM-2005-214062, 2005.

[3] Graham R E, Hughes J E, Moseley W C.Aerodynamic Stability Characteristics of the Apollo Command Module[R].NASA-TN-D-4688, 1968.

[4] 詹慧玲, 陈冰雁, 刘周, 等.典型再入返回器气动特性对比与改进研究[J].航天返回与遥感, 2013, 34（6）: 11-20.

ZHAN Huiling, CHEN Bingyan, LIU Zhou,et al.Comparative Study and Improvement Desgin on Aerodynamic Characteristics of Typical Reentry Capsules[J].Spacecraft Recovery & Remote Sensing, 2013, 34（6）: 11-20.（in Chinese）

[5] Roe P.Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes[J].Journal of Computational Physics, 1997,135（2）: 250-258.

[6] LIU Zhou, ZHOU Weijiang.Adaptive Viscous Cartesian Grid Generation and Application[J].ACTA Aeronautica et Astronautica Sinica, 2009, 30（12）: 2280-2287.

[7] Spalart P, Allmaras S.A One-equation Turbulent Model for Aerodynamic Flows[R].AIAA 1993-0880, 1993.

[8] Wilcox D C.Reassessment of the Scale-determining Equation for Advanced Turbulence Models[J].AIAA Journal, 1988,26（11）: 1299-1310.

[9] Wilcox D C.Turbulence Modeling for CFD[M].3rd edition.DCW Industries, Inc., La Canada CA, 2006.

[10] Menter F R.Two-equation Eddy-viscosity Turbulence Models for Engineering Applications[J].AIAA Journal, 1994, 32（8）:1598-1605.