钢管下料问题的Mathematica求解及分析

2014-07-18隋英孙常春艾瑛

决策与信息 2014年30期

关键词：下料根数用料

隋英孙常春艾瑛

沈阳建筑大学理学院辽宁沈阳 110168

钢管下料问题的Mathematica求解及分析

隋英孙常春艾瑛

沈阳建筑大学理学院辽宁沈阳 110168

针对钢管切割加工的问题，分别以余料最少和用料最省为目标，建立了该问题的整数规划模型，并用Mathemaica软件进行求解。同时，对两个模型进行了比较分析，得出了以用料最省为目标建立的模型优于以余料最少为目标建立的模型的结论，寻求出了钢管下料的最佳处理方案。

线性规划；整数规划；Mathemaica

生活中常会遇到切割、裁剪、冲压等手段，将原材料加工成所需大小，这种工艺过程称为原料下料问题。按照进一步的工艺要求，确定下料方案，使用料最省或利润最大。本文针对一类钢管的切割加工问题，建立了数学模型，并用Mathemaica软件进行了求解。

问题提出

某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割后售出。从钢管厂进的原料钢管都是19米长，现有一客户需要50根4米长、20根6米长、15根8米长的钢管，应如何下料最节省？

问题分析

首先，应当确定哪些切割模式是可行的。所谓一个可行的切割模式，是指能按照客户需要在原料钢管上安排切割的一种组合。例如：将19米长的钢管切割成3根4米长的钢管，余料为7米；或者将19米长的钢管切割成4米、6米和8米长的钢管各1根，余料为1米。通常，可行的切割模式是只要能按照客户的要求进行切割就行，而不必考虑该切割模式是否合理。显然，可行的切割模式是很多的。

其次，应当确定哪些切割模式是合理的。通常假设一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸。例如：将19米长的钢管切割成3根4米长的钢管的切割模式是可行的，但余料为7米，可以进一步将7米的余料切割成4米钢管余料为3米，或将7米的余料切割成6米的钢管余料为1米。在这种假设下，合理的切割模式一共有7种，如表1所示：

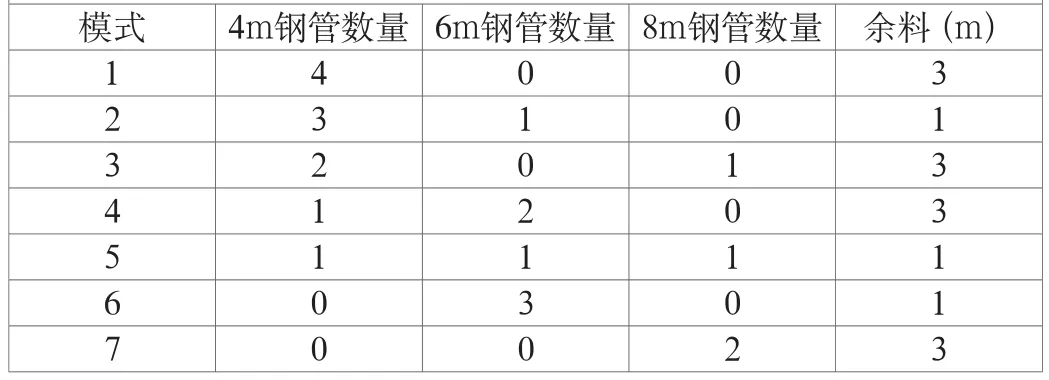
表1 钢管下料的合理切割模式

问题化为在满足客户需要的条件下，按照哪种合理的模式，切割多少根原料钢管，最为节省的问题。所谓的节省，可以有两种标准，一是切割后剩余的总余料量最小，二是切割原料钢管的总根数最少。以此为目标，可建立下述模型。

模型的建立和求解

决策变量：设xi表示按第i种模式i=1，2，L，7切割的原料钢管的数量，xi为非负的整数。

约束条件：4米的钢管要50根，则：4x1+3x2+2x3+x4+x5≥50；

6 米的钢管要20根，则：x2+2x4+x5+3x6≥20；

8 米的钢管要15根，则：x3+x5+2x7≥15；

整数约束：xi为非负的整数，i=1，2，L，7。

目标函数：如果以切割后剩余的总余料量最小为目标，可得：

minz =3x1+x2+3x3+3x4+x5+x6+3x7于是以切割后剩余的总余料量最小为目标，可得模型（1）

xi为非负的整数，i=1，2，L，7

利用Mathematica求解模型

即：按照模式2切割12根原料钢管，按照模式5切割15根原料钢管，共27根，总余料为27米。

目标函数：如果以切割原料钢管的总根数最少为目标，则有

于是以切割原料钢管的总根数最少为目标，可得模型（2）：

xi为非负的整数，i=1，2，L，7

利用Mathematica求解模型

即：按照模式2切割15根原料钢管，按照模式5切割5根原料钢管，按照模式7切割5根原料钢管，共25根，总余料量为35米。

模型的比较分析

经计算得：模型（1）按照模式2切割12根原料钢管，按照模式5切割15根原料钢管，共用料27根，总余料为27米。按照模型（1）的切割方式，共得到了36+15=51根4米长的钢管，12+15=27根6米长的钢管，15根8米长的钢管。而实际客户需要的是50根4米长、20根6米长、15根8米长的钢管。因此，模型（1）实际用料27根，多生产了1根4米长的钢管、7根6米长的钢管，实际的总余料为27+4+42=73米。

经计算得：模型（2）按照模式2切割15根原料钢管，按照模式5切割5根原料钢管，按照模式7切割5根原料钢管，共用料25根，总余料量为35米。按照模型（2）的切割方式，共得到了45+5=50根4米长的钢管，15+5=20根6米长的钢管，5+10=15根8米长的钢管。刚好满足客户的要求，仅用料25根，余料35米。

经分析可得：仅在一次的供货时，在余料没有什么用途的情况下，无论是以切割后实际剩余的总余料量最小为目标，还是以切割原料钢管的总根数最少为目标，模型（2）都较模型（1）更好。