部分射开直井的产能计算方法

李龙龙，吴明录，姚 军，李 阳，2，李晓雪

（1.中国石油大学（华东）石油工程学院，山东青岛266580；2.中国石化油田勘探开发事业部，北京100029）

射孔完井作为油气井的主要完井方式［1］，研究其产能计算具有现实意义。由于地质或工程原因，储层未完全钻穿或未全部射开［2］，加上射孔因素和钻井污染的影响［3－8］，计算部分射开直井的产能存在一定难度。1966年，M.H.Harris［9］运用有限差分法建立了理想射孔时射孔直井产能的数学模型；J.A.Klotz等人［10］将三维流动简化为二维流动，运用有限元法研究了压实损害带对产能的影响；H.O.McLeod Jr.［11］提出了射孔井的简化模型，并分别求出污染带和射孔压实带的表皮系数；Metin Karakas等人［12］运用有限元法得到射孔表皮系数；唐愉拉等人［13－14］论述了有限元数学模型的建立及数值求解方法，并研究了各种参数对射孔油气井产能的影响规律；郎兆新等人［15］运用有限元法和非线性回归法得出21个回归公式；李祥贵等人［16］采用有限元法研究了各种射孔参数对表皮系数和产率比的影响规律。对于部分射开对产能的影响主要通过部分射开表皮系数确定，其计算方法主要有3种［17－18］，都是对问题进行简化后通过经验公式或数值模拟方法得到的。

现有部分射开直井的产能计算方法，主要是通过分别求取射开程度、射孔参数、射孔压实带以及污染带的表皮系数来计算产能，对问题进行了割裂、简化处理。为此，笔者将McLeod射孔几何模型改进为双径向流模型，应用渗流力学原理和等值渗流阻力法，分各向同性油藏射穿与未射穿污染带、各向异性油藏射穿与未射穿污染带等4种情况，得到部分射开直井的产能计算方法，该计算方法充分考虑了射孔深度、射孔密度、孔径、相位角、压实带、射开程度、污染带、各向异性等因素以及这些因素之间的相互影响。

1 各向同性油藏部分射开直井的产能计算方法

考虑单层、均质、各向同性、圆形定压边界油藏中心有一口部分射开直井的情况，对油藏、流体及射孔效果做如下假设：1）油藏中的流体为单相，流动规律符合达西定律；2）油藏中的岩石和流体均不可压缩；3）井筒周围存在污染带，孔眼周围存在射孔压实带；4）忽略流体在孔眼中流动的压力损失；5）忽略毛管力和重力的影响。基于以上假设，对各向同性油藏部分射开直井分孔眼射穿污染带和孔眼未射穿污染带2种情况进行产能计算方法研究。

1.1 未射穿污染带

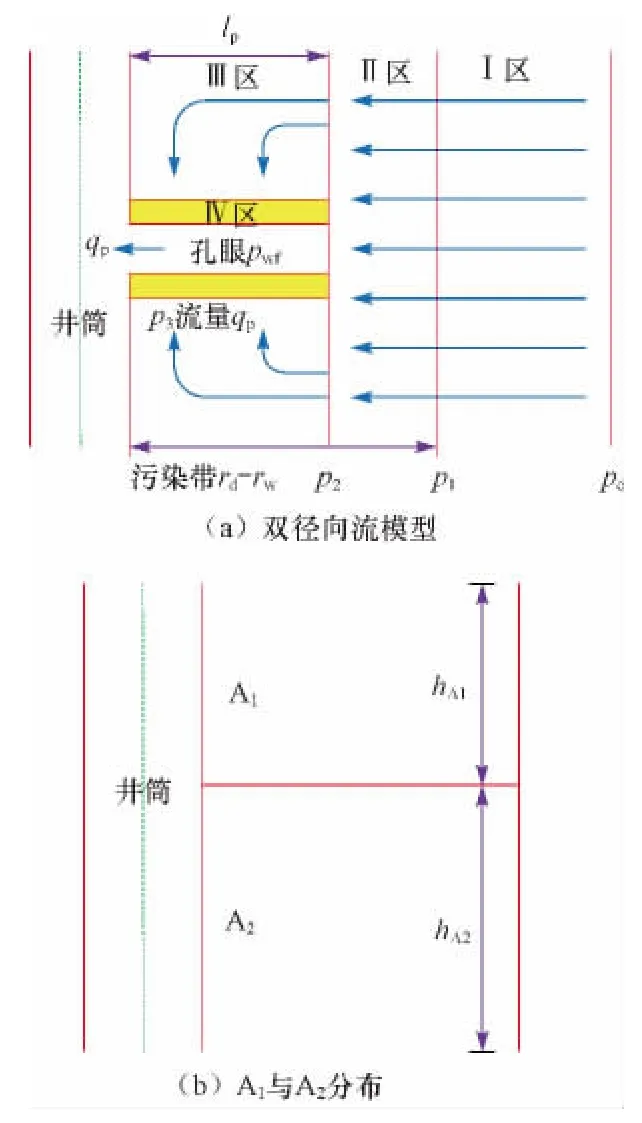
图1 未射穿污染带的双径向流模型Fig.1 The dual radial flow model in the condition of partially penetrated damaged－zone

基于以上假设，对McLeod射孔几何模型进行改进，当孔眼未射穿污染带时，双径向流模型如图1（a）所示，射孔完井后流体的流动主要分为：油藏外边界向孔眼射穿区外边界的流动和孔眼射穿区围绕孔眼的径向流（与未射开区相邻的射孔周期内围绕孔眼的流动采用偏心径向流，其他射孔周期内围绕孔眼的流动采用非偏心径向流）。因此，将油藏分为2部分（见图1（b）），A1代表与未射开区相邻的射孔周期以外的射开区，A2代表未射开区加上与未射开区相邻的射孔周期。其中，A1和A2的厚度可表示为：

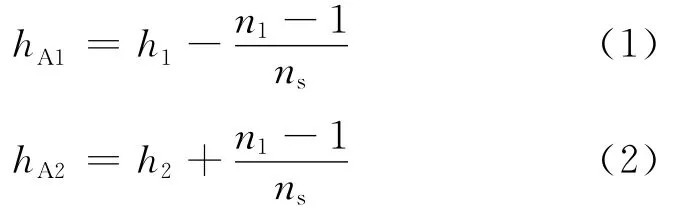
式中：hA1为A1区的厚度，m；h1为射开油层厚度，m；n1为一个射孔周期内的孔眼数（n1＝360／θ，θ为相位角，即相邻2个孔眼之间的夹角，取45°、60°、90°、120°和180°）；ns为射孔孔眼密度，孔／m；hA2为A2区的厚度，m；h2为未射开油层厚度，m。

应用等值渗流阻力法［19］描述双径向流的渗流过程，求解未射穿污染带时的产能。

1.1.1 Ⅰ区渗流阻力

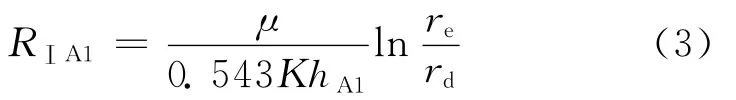
Ⅰ区为储层的未污染区，流动为水平径向流，外边界半径为油藏半径，内边界半径为污染带半径，高度为油藏厚度，渗透率为油藏原始渗透率，则与A1对应部分的渗流阻力为：式中：RⅠA1为Ⅰ区与A1对应部分的渗流阻力，MPa·d／m3；μ为流体黏度，mPa·s；h为油藏厚度，m；re为油藏半径，m；rd为污染带半径，m；h为油藏厚度，m；K为油藏原始渗透率，mD。

与A2对应部分的渗流阻力为：

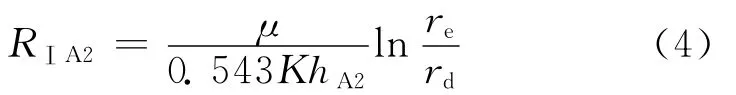
式中：RⅠA2为Ⅰ区与A2对应部分的渗流阻力，MPa·d／m3。

1.1.2 Ⅱ区渗流阻力

Ⅱ区为孔眼未射穿的污染带，流体为水平径向流，外边界半径为污染带半径，内边界半径为水泥环外半径和孔眼长度之和，高度为油藏厚度，渗透率考虑钻井过程中钻井液对油藏的污染。则与A1对应部分的渗流阻力为：

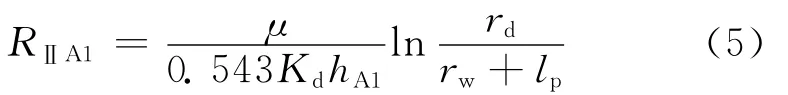
式中：RⅡA1为Ⅱ区与A1对应部分的渗流阻力，MPa·d／m3；rw为水泥环的外半径，m；lp为孔眼长度，m；Kd为污染带的渗透率，mD。

与A2对应部分的渗流阻力为：

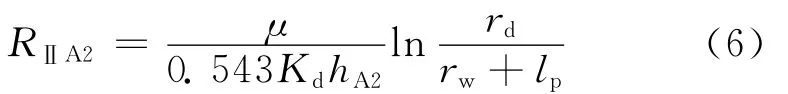
式中：RⅡA2为Ⅱ区与A2对应部分的渗流阻力，MPa·d／m3。

1.1.3 Ⅲ区渗流阻力

Ⅲ区为孔眼射穿的污染带，根据渗流力学中关于偏心径向流的假设条件可知，与A2对应部分的孔眼（与未射开区域相邻的射孔周期内的孔眼）的流体流动为围绕孔眼的垂直平面偏心径向流（见图2），第i个孔眼（从与未射穿区相邻的第一个孔眼算起，1≤i≤n1）的径向流半径为ri（hp为两个相邻的相位相同的孔眼之间距离的一半），偏心距为di；与A1对应部分的孔眼（共n2个）周围的流体流动为围绕孔眼的垂直平面非偏心径向流（见图3），外边界半径为hp，内边界半径为压实带半径rc，该区渗透率为Kd。

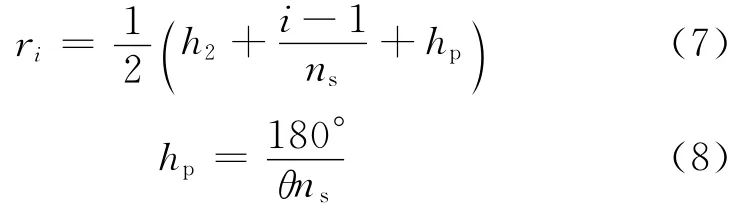
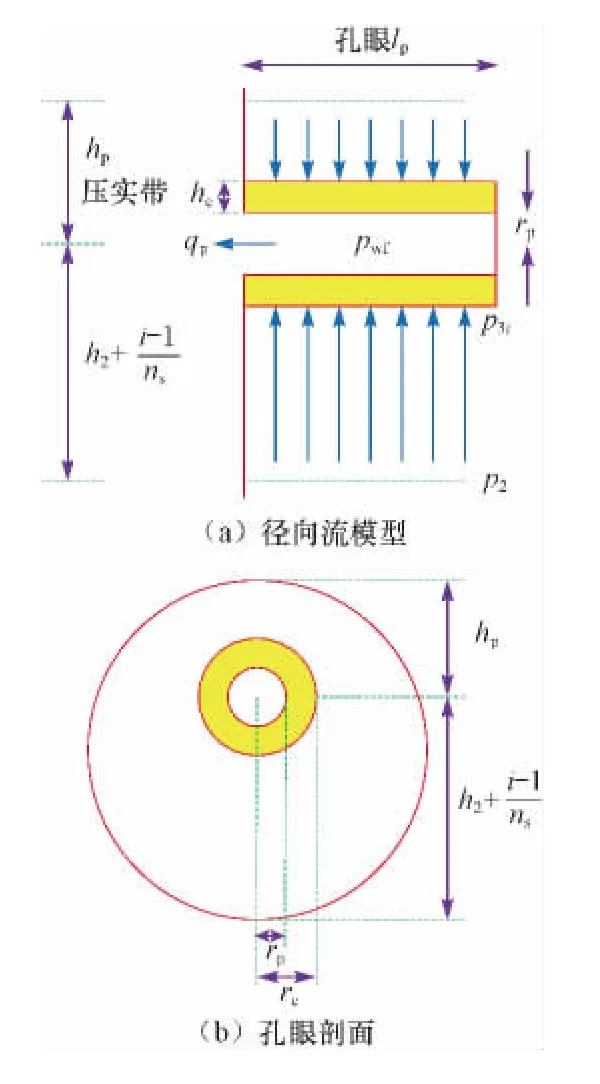
图2 未射穿污染带时与未射开区域相邻的射孔周期内第i个孔眼周围的径向流模型Fig.2 The eccentric radial flow of perforating hole which is adjacent to the unperforated zone and in perforation cycle

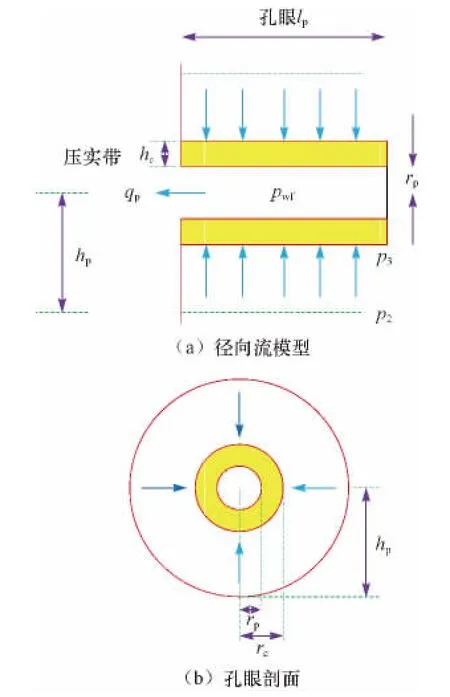
图3 未射穿污染带时与未射开区域相邻的射孔周期以外孔眼周围的径向流模型Fig.3 The concentric radial flow of perforating hole which is adjacent to the unperforated zone but not in the perforation cycle

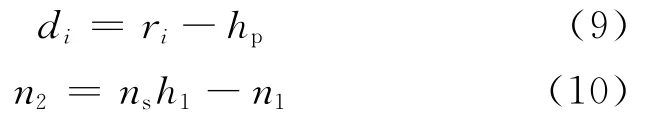
式中：ri为第i个孔眼的径向流半径，m；hp为2个相邻的相位相同孔眼之间距离的一半，m；di为第i个孔眼的偏心距，m；n2为A1部分的孔眼数；rp为孔眼半径，m；hc为压实带厚度，m。

与A2对应部分，围绕第i个孔眼的流体流动为偏心径向流，跟垂直平面内围绕水平井的径向流动类似，因此借鉴S.D.Joshi［20］和陈元千等人［21］推导水平井产能公式时考虑偏心距的方法，得流量方程为：

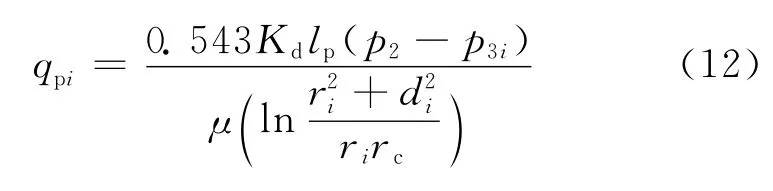
式中：qpi为与A2对应部分的第i个孔眼的流量，m3／d。

其渗流阻力为：

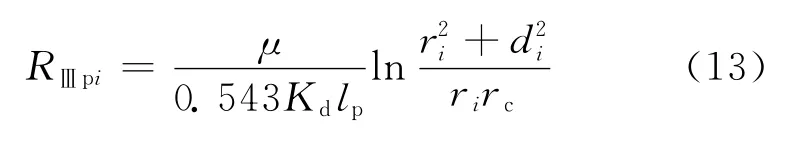
式中：RⅢpi为Ⅲ区与A2对应部分的第i个孔眼周围流体流动的渗流阻力，MPa·d／m3。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

式中：RⅢp为Ⅲ区与A1对应部分的单个孔眼周围流体流动的渗流阻力，MPa·d／m3。

1.1.4 Ⅳ区渗流阻力

Ⅳ区为射孔压实带，流动为围绕孔眼的垂直平面径向流，外边界半径为压实带半径，内边界半径为孔眼半径，渗透率考虑到射孔过程中对孔眼周围产生的压实损害。则与A2对应部分，第i个孔眼周围流体流动的渗流阻力为：

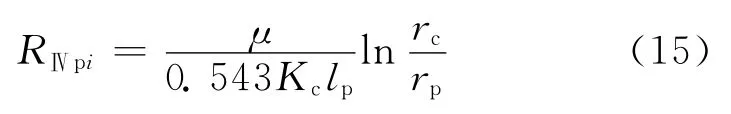
式中：RⅣpi为Ⅳ区与A2对应部分的第i个孔眼周围流体流动的渗流阻力，MPa·d／m3；Kc为压实带的渗透率，mD。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

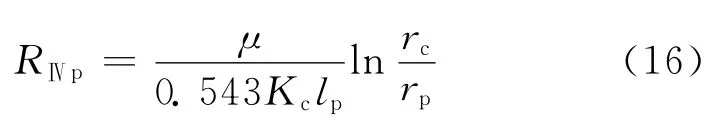
式中：RⅣp为Ⅳ区与A1对应部分的单个孔眼周围流体流动的渗流阻力，MPa·d／m3。

1.1.5 总的渗流阻力及产能

由等值渗流阻力法可知，A2区中的单个孔眼，其在Ⅲ区、Ⅳ区的渗流阻力为串联关系，可得围绕第i个孔眼的流体流动的渗流阻力Rpi＝RⅢpi＋RⅣpi；A1区中的单个孔眼在Ⅲ区与Ⅳ区的渗流阻力也为串联关系，可得围绕单个孔眼的流体流动的渗流阻力Rp＝RⅢp＋RⅣp。则A1区的总渗流阻力为：

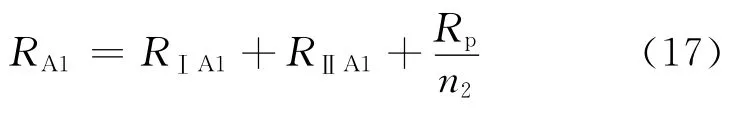
式中：RA1为 A1区的总渗流阻力，MPa·d／m3。A2区的总渗流阻力为：

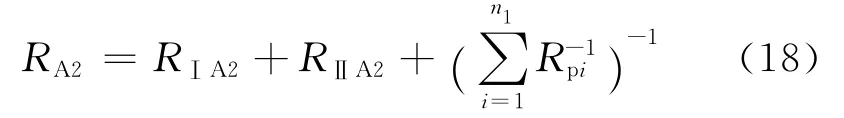
式中：RA2为 A2区的总渗流阻力，MPa·d／m3。

A1区与A2区之间渗流阻力为并联关系，可得油藏的总渗流阻力：

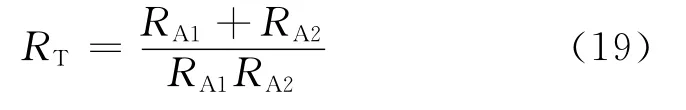
式中：RT为油藏流体流动的总渗流阻力，MPa·d／m3。

根据油藏流体流动的总渗流阻力，可得未射穿污染带时部分射开井的产能：

式中：q为部分射开井的产量，m3／d；Δp为生产压差，MPa；B为原油的体积系数。

1.2 射穿污染带

基于对油藏、流体及射孔效果的假设，对McLeod射孔几何模型进行改进，当孔眼射穿污染带时，双径向流模型如图4所示，射孔完井后流体的流动主要分为油藏外边界向孔眼射穿区外边界的流动以及孔眼射穿区围绕孔眼的径向流（与未射开区相邻的射孔周期内围绕孔眼的流动采用偏心径向流，其他射孔周期内围绕孔眼的流动采用非偏心径向流），A1和A2区的分布见图1。应用等值渗流阻力法描述双径向流渗流过程，求解射穿污染带时的产能。

图4 射穿污染带的双径向流模型Fig.4 The dual radial flow model in the condition of penetrated damaged－zone

1.2.1 Ⅰ′区渗流阻力

Ⅰ′区为储层的未射穿区，流动为水平径向流，外边界半径为油藏半径，内边界半径为水泥环外半径和孔眼长度之和，高度为油藏厚度，渗透率为油藏原始渗透率。则与A1对应部分的渗流阻力为：

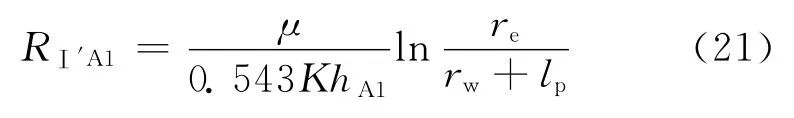
式中：RⅠ′A1为Ⅰ′区与 A1对应部分的渗流阻力，MPa·d／m3。

与A2对应部分的渗流阻力为：

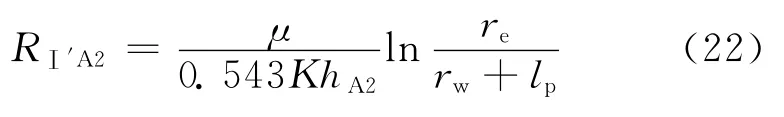
式中：RⅠ′A2为Ⅰ′区与A2对应部分的渗流阻力，MPa·d／m3。

1.2.2 Ⅱ′区渗流阻力

Ⅱ′区为孔眼射穿的未污染区，与A2对应部分，流体流动为围绕孔眼的垂直平面偏心径向流（见图5），其半径、偏心距与未射穿污染带的偏心径向流相同，孔眼剖面如图2（b）所示；与A1对应部分，孔眼周围的流体流动为围绕孔眼的垂直平面非偏心径向流（见图6），孔眼剖面如图3（b）所示，外边界半径为hp，内边界半径为压实带半径，渗透率为油藏原始渗透率。

图5 射穿污染带时与未射开区域相邻的射孔周期内第i个孔眼周围的径向流模型Fig.5 The eccentric radial flow of perforating hole which is adjacent to the unperforated zone and in perforation cycle

与A2对应部分，围绕第i个孔眼的流体流动为偏心径向流，流量方程为：

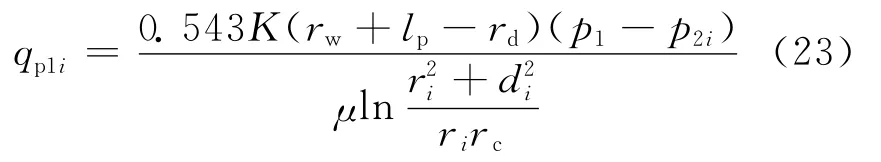
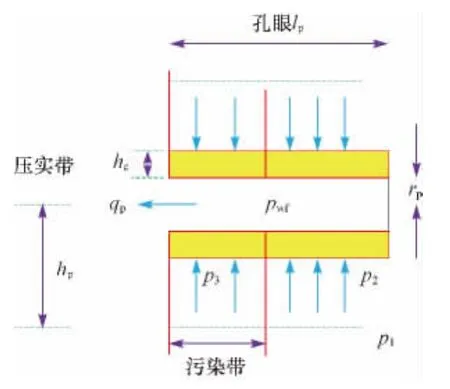
图6 射穿污染带时与未射开区域相邻的射孔周期以外孔眼周围的径向流模型Fig.6 The concentric radial flow of perforating hole which is adjacent to the unperforated zone but not in the perforation cycle

式中：qp1i为Ⅱ′区与A2对应部分的第i个孔眼的流量，m3／d。

其渗流阻力为：

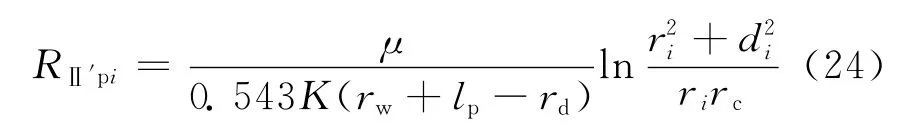
式中：RⅡ′pi为Ⅱ′区与A2对应部分的第i个孔眼周围流体流动的渗流阻力，MPa·d／m3。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

式中：RⅡ′p为Ⅱ′区与A1对应部分的单个孔眼周围流体流动的渗流阻力，MPa·d／m3。

1.2.3 Ⅲ′区渗流阻力

Ⅲ′区为孔眼射穿的污染区，与A2对应部分，流体流动为围绕孔眼的垂直平面偏心径向流（见图5），半径、偏心距与未射穿污染带的偏心径向流相同；与A1对应部分，孔眼周围的流体流动为围绕孔眼的垂直平面非偏心径向流（见图6），外边界半径为hp，内边界半径为压实带半径，渗透率为污染带渗透率。则与A2对应部分，围绕第i个孔眼的流动为偏心径向流，其流量方程为：

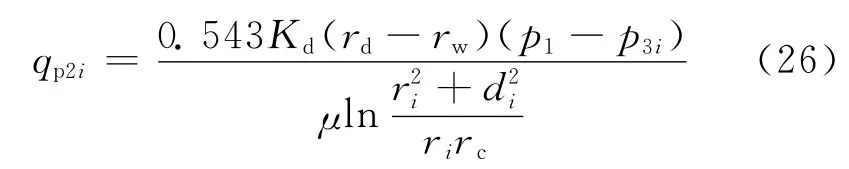
式中：qp2i为Ⅲ′区与A2对应部分的第i个孔眼的流量，m3／d。

其渗流阻力为：

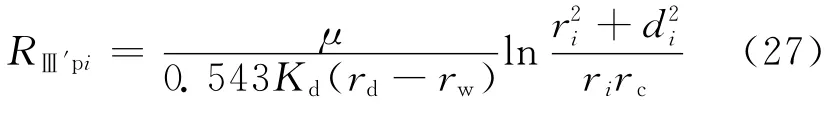
式中：RⅢ′pi为Ⅲ′区与A2对应部分的第i个孔眼周围流体流动的渗流阻力，MPa·d／m3。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

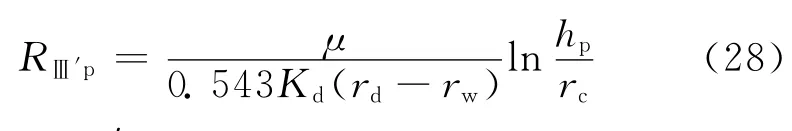
式中：RⅢ′p为Ⅲ′区与A1对应部分的单个孔眼周围流体流动的渗流阻力，MPa·d／m3。

1.2.4 Ⅳ′区渗流阻力

Ⅳ′区为非污染区的射孔压实带，流动为围绕孔眼的垂直平面径向流，外边界半径为压实带半径rc，内边界半径为孔眼半径rp，渗透率为Kc1。则与A2对应部分，围绕第i个孔眼的流体流动的渗流阻力为：

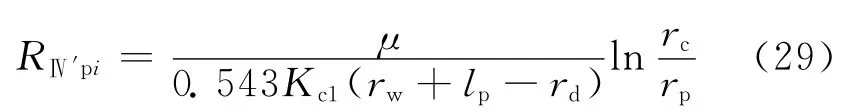
式中：RⅣ′pi为Ⅳ′区与A2对应部分的第i个孔眼周围流体流动的渗流阻力，MPa·d／m3。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

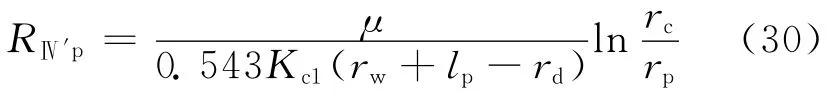
式中：RⅣ′p为Ⅳ′区与A1对应部分的单个孔眼周围流体流动的渗流阻力，MPa·d／m3。

1.2.5 Ⅴ′区渗流阻力

Ⅴ′区为污染区的射孔压实带，流动为围绕孔眼的垂直平面径向流，外边界半径为压实带半径rc，内边界半径为孔眼半径rp，渗透率为Kc2。则与A2对应部分，围绕第i个孔眼的流体流动的渗流阻力为：

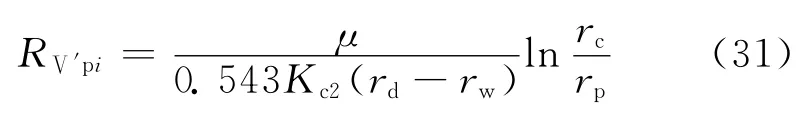
式中：RⅤ′pi为Ⅴ′区与A2对应部分的第i个孔眼周围流体流动的渗流阻力，MPa·d／m3。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

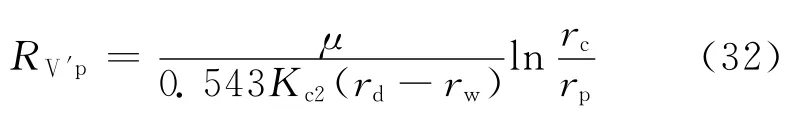
式中：RⅤ′p为Ⅴ′区与A1对应部分的单个孔眼周围流体流动的渗流阻力，MPa·d／m3。

1.2.6 总的渗流阻力及产能

孔眼射穿区中，单个孔眼在Ⅱ′、Ⅳ′区的渗流阻力以及单个孔眼在Ⅲ′、Ⅴ′区的渗流阻力均为串联关系，而对于同一个孔眼，Ⅱ′、Ⅳ′区串联后的渗流阻力与Ⅲ′、Ⅴ′区串联后的渗流阻力之间为并联关系。因此，与A2对应部分，围绕第i个孔眼的流体流动的渗流阻力为：

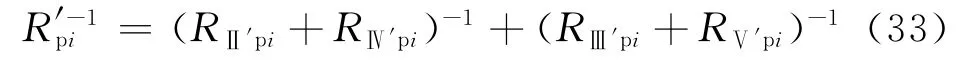
式中：R′pi为与A2对应部分的第i个孔眼的渗流阻力，MPa·d／m3。

与A1对应部分，单个孔眼周围流体流动的渗流阻力为：

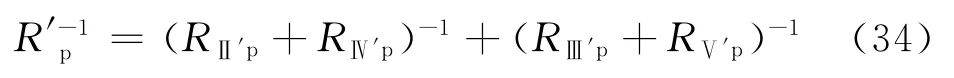
式中：R′p为与A1对应部分的单个孔眼的渗流阻力，MPa·d／m3。

A1区总的渗流阻力为：

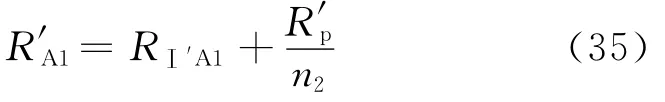
式中：R′A1为与A1对应部分的总渗流阻力，MPa·d／m3。

A2区的总渗流阻力为：

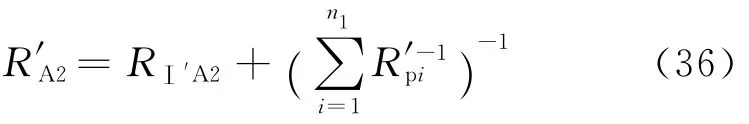
式中：R′A2为与A2对应部分的总渗流阻力，MPa·d／m3。

以上2个渗流阻力之间为并联关系，可得油藏的总渗流阻力：

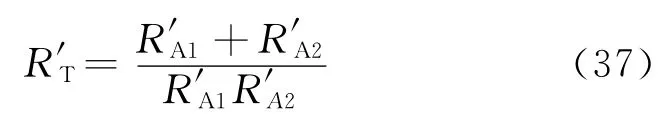
式中：R′T为油藏流体流动的总渗流阻力，MPa·d／m3。

根据油藏流体流动的总渗流阻力，可得射穿污染带时部分射开井的产能为：

2 各向异性油藏部分射开直井的产能计算方法

各向异性油藏与各向同性油藏的差别导致各向异性油藏部分射开直井的产能计算方法不同，考虑污染带和压实带的影响，将各向异性油藏的渗流区域分为非污染区、污染区、压实带。

根据各向异性油藏渗流理论［22－23］，将各向异性油藏变换为等价的各向同性油藏：油藏原始渗透率校正藏厚度校正为h′＝hβ2／3，藏射开厚度校正为h′1＝，油藏未射开厚度校正为h′2＝，油藏半径校正筒半径校正孔深度 校 正孔 直 径 校 正 为r′＝p孔密度校正染带渗透率校正污染带半径校正压实带渗透率校正压实带半径校绕孔眼的非偏心径向流半径校正为h′p＝，偏心径向流半径校正心距校正为d′i＝（ri－hp）·β2／3。其中，Kh为未污染区的水平渗透率，D；Kv为垂直渗透率，D；Kdh为污染区的水平渗透率，D；Kdv为垂直渗透率，D；Kch为射孔压实带的水平渗透率，D；Kcv为垂直渗透率，D。

基于与各向同性油藏未射穿污染带时相似的原理，各向异性油藏未射穿污染带时的渗流阻力求解方法为：将校正后的参数代入式（3）、（4），得到Ⅰ区的渗流阻力RⅠA1与RⅠA2，代入式（5）、（6）得到Ⅱ区的渗流阻力RⅡA1与RⅡA2，代入式（13）、（14）得到Ⅲ区孔眼的渗流阻力RⅢpi与RⅢp，代入式（15）、（16）得到Ⅳ区孔眼的渗流阻力RⅣpi与RⅣp，由以上各区的渗流阻力可得油藏的总渗流阻力，最后得到各向异性油藏未射穿污染带时部分射开直井的产能。

基于与各向同性油藏射穿污染带时相似的原理，各向异性油藏射穿污染带时的渗流阻力求解方法为：将校正后的参数代入式（21）、（22）得到Ⅰ区的渗流阻力RⅠ′A1与RⅠ′A2，代入式（24）、（25）得到Ⅱ区孔眼的渗流阻力RⅡ′pi与RⅡ′p，代入式（27）、（28）得到Ⅲ区孔眼的渗流阻力RⅢ’pi与RⅢ′p，代入式（29）、（30）得到Ⅳ区孔眼的渗流阻力RⅣ′pi与RⅣ′p，代入式（31）、（32）得到Ⅴ区孔眼的渗流阻力RⅤ′pi与RⅤ′p，由以上各区的渗流阻力可得油藏的总渗流阻力，最后得到各向异性油藏射穿污染带时部分射开直井的产能。

3 参数敏感性分析

油藏厚度为20m，射开厚度为15m（上部射开），供油半径为300m，井筒半径为10cm，供给边界压力为25MPa，井底压力为17MPa，油藏原始渗透率为20mD，污染带半径为70cm，渗透率为12mD，射孔压实带厚度为1.2cm，压实程度为70%（渗透率为射孔前的30%），流体黏度为9mPa·s，体积系数为1.1。图7—12中，射孔深度0.6m（60cm）为射穿污染带与未射穿污染带的分界。

首先，比较了射孔深度和井筒半径之和与污染带半径的关系，以判断孔眼是否射穿污染带，选择了相应的产能计算方法；然后，分别计算了各区的渗流阻力，并得到了总的渗流阻力；最后，由总的渗流阻力得到了部分射开直井的产能。在此基础上，分析产量对射开程度、射孔深度、射孔密度、孔径、相位、压实程度、压实带厚度的敏感性。

3.1 射开程度

射孔直径为1.2cm、射孔密度为20孔／m、相位角为90°时，分别取射开程度为50%，60%，70%，80%，90%和100%，研究不同射开程度时产量随射孔深度的变化关系，结果见图7。由图7可知：1）当射孔深度（或射开程度）一定时，产量随着射开程度（或射孔深度）的增大而增大；2）随着射孔深度的增大，产量对射开程度的敏感性逐渐降低，未射穿污染带时比射穿污染带时高；3）在射开程度相同的情况下，随着射孔深度的增大，产量对射孔深度的敏感性逐渐降低，未射穿污染带时比射穿污染带时高。

图7 不同射开程度时产量随射孔深度的变化关系Fig.7 The effect of perforation length on productivity at different perforated degree

3.2 射孔密度

射孔直径为1.2cm、相位角为90°时，分别取射孔密度5，10，15，20，25，30，35和40孔／m，研究不同射孔密度时产量随射孔深度的变化关系，结果见图8。由图8可知：1）当射孔深度一定时，产量随着射孔密度的增大而增大；2）随着射孔深度的增大，产量对射孔密度的敏感性逐渐减小，未射穿污染带时比射穿污染带时高；3）在射孔深度相同的情况下，射孔密度较小时，产量对射孔密度非常敏感，但随着射孔密度的增大，敏感性逐渐降低，当射孔密度达到一定程度之后，敏感性不再明显。

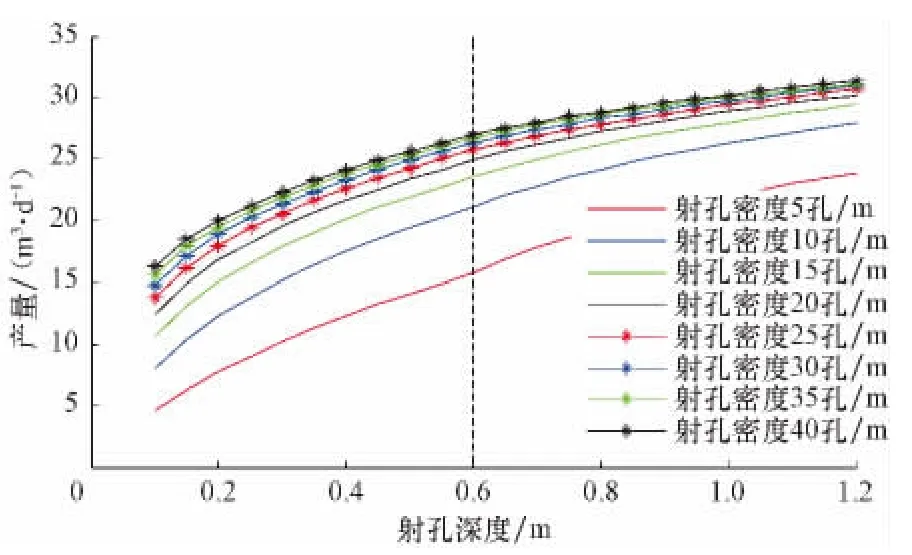
图8 不同射孔密度时产量随射孔深度的变化关系Fig.8 The effect of perforation length on productivity at different shot density

3.3 射孔直径

射孔密度为20孔／m、相位角为90°时，在射孔直径取值范围（0.8～1.2cm）内，分别取射孔直径为0.8，0.9，1.0，1.1和1.2cm，研究不同射孔直径时产量随射孔深度的变化关系，结果见图9。由图9可知：1）当射孔深度一定时，产量随着射孔直径的增大而增大；2）随着射孔深度的增大，产量对孔射孔直径的敏感性逐渐减小，未射穿污染带时比射穿污染带时高；3）在射孔深度相同的情况下，产量对射孔直径的敏感性比较小。

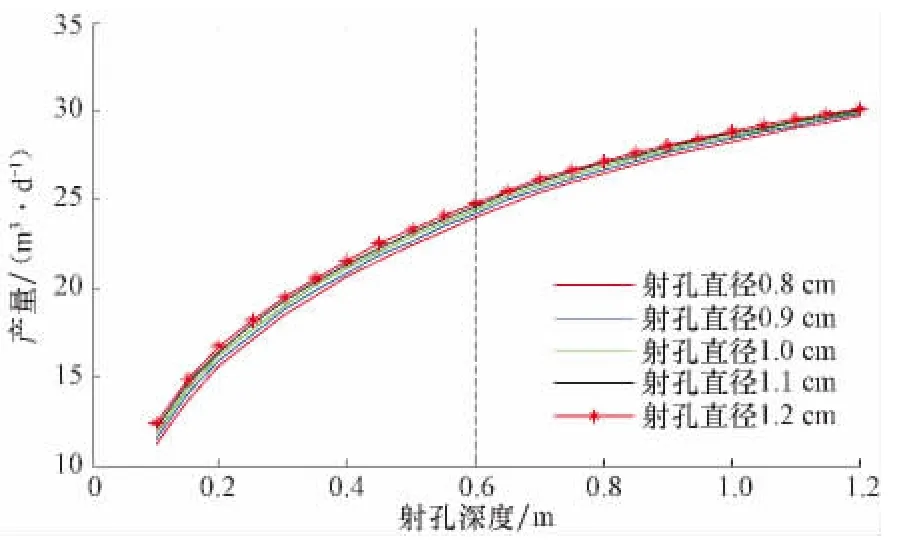
图9 不同射孔直径时产量随射孔深度的变化关系Fig.9 The effect of perforation length on productivity at different perforation diameter

3.4 相位角

射孔直径为1.2cm、射孔密度为20孔／m时，分别取相位角为45°，60°，90°，120°和180°，得到不同相位时产量随射孔深度的变化关系，结果见图10。由图10可知：1）当射孔深度一定时，产量随相位角的增大而增大；2）随着射孔深度的增大，产量对相位角的敏感性逐渐减小，未射穿污染带时比射穿污染带时高；3）在射孔深度相同的情况下，产量对相位角的敏感性比较小。

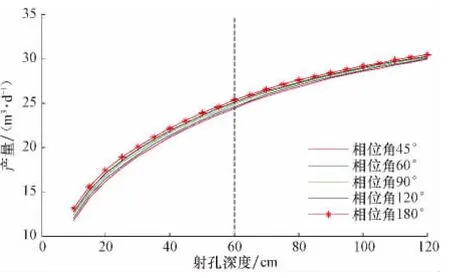
图10 不同相位时产量随射孔深度的变化关系Fig.10 The effect of perforation length on productivity at different phasing

3.5 压实程度

射孔直径为1.2cm、射孔密度为20孔／m、相位角90°时，压实程度分别取50%，55%，60%，65%，70%，75%，80%和85%，得到不同压实程度时产量随射孔深度的变化关系曲线，结果见图11。由图11可知：1）当射孔深度一定时，产量随压实程度的增大而减小；2）随着射孔深度的增大，产量对压实程度的敏感性逐渐减小，未射穿污染带时比射穿污染带时高；3）在射孔深度相同的情况下，压实程度较高时，产量对压实程度非常敏感，但随着压实程度的减小，敏感性逐渐降低，当压实程度减小到一定程度之后，敏感性不再明显。

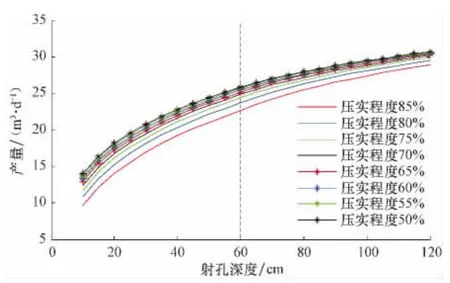
图11 不同压实程度时产量随射孔深度的变化关系Fig.11 The effect of perforation length on productivity at different compaction degree of crushed zone

3.6 压实带厚度

射孔直径为1.2cm、射孔密度为20孔／m、相位角90°时，压实带厚度分别取 0.6，0.7，0.8，0.9，1.0，1.1，1.2和1.3cm，研究不同压实带厚度时产量随射孔深度的变化关系，结果见图12。由图12可知：1）当射孔深度一定时，产量随压实带厚度的增大而减小；2）随着射孔深度的增大，产量对压实带厚度的敏感性逐渐减小，未射穿污染带时比射穿污染带时高；3）在射孔深度相同的情况下，产量对压实带厚度的敏感性非常小。

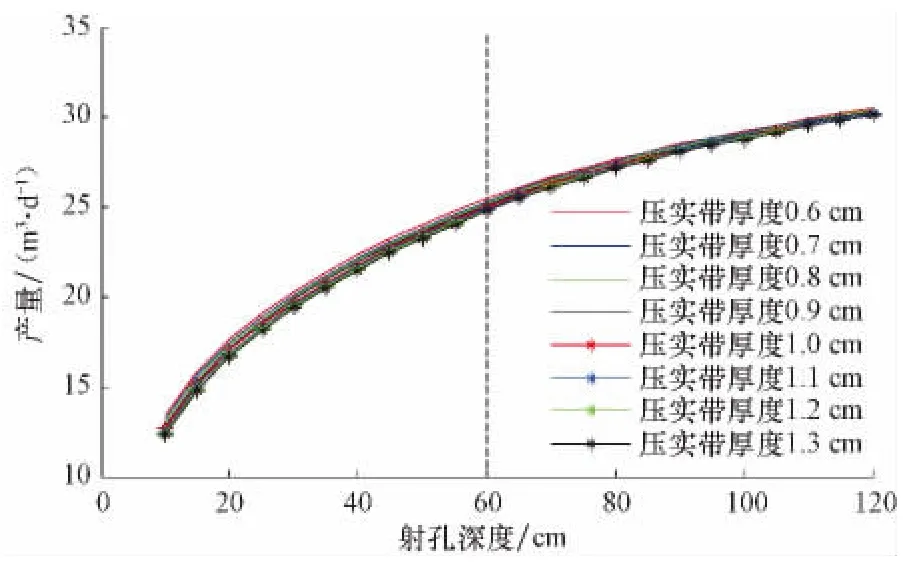
图12 不同压实带厚度时产量随射孔深度的变化关系Fig.12 The effect of perforation length on productivity at different crush zone thickness

4 不同方法的计算结果对比

对于部分射开直井，常用表皮系数法［18］进行产能计算。根据上述油藏参数，分别利用新方法和表皮系数法计算不同射孔方案（见表1）的产量，结果见图13。

由图13可知，新方法计算得到的产量略低于表皮系数法计算得到的产量，相差约为5%。分析认为，两者相差的原因为：

1）表皮系数法是分别求取射开程度、射孔参数、污染带以及射孔压实带的表皮系数，然后计算产能，对问题进行了割裂、简化处理，没有充分考虑以上各因素之间的相互影响。例如，部分射开表皮系数描述的只是直井裸眼完井时部分储层打开对产能的影响，不是射孔完井时部分射开对产能的影响，而且表皮系数法虽然考虑了是否射穿污染带对产能的影响，但是对该问题进行了简化处理：当孔眼未射穿污染带时修正射孔表皮系数，当孔眼射穿污染带时修正射孔深度和井筒半径，且修正过程中不考虑射孔压实损害带的影响。

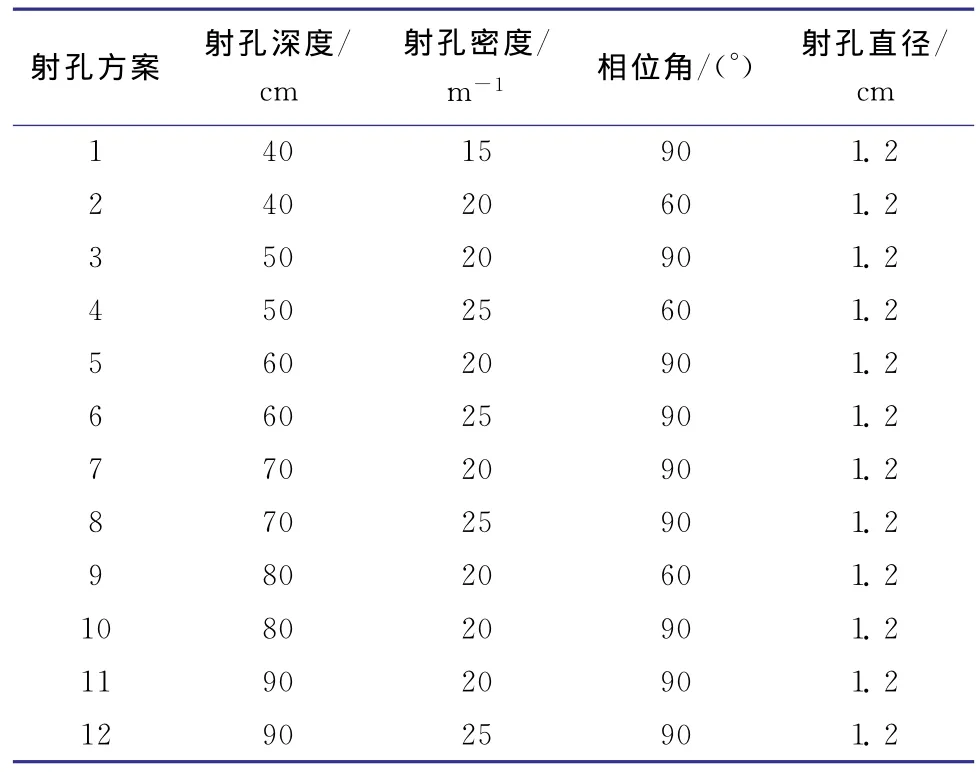
表1 射孔方案Table 1 Perforation scheme

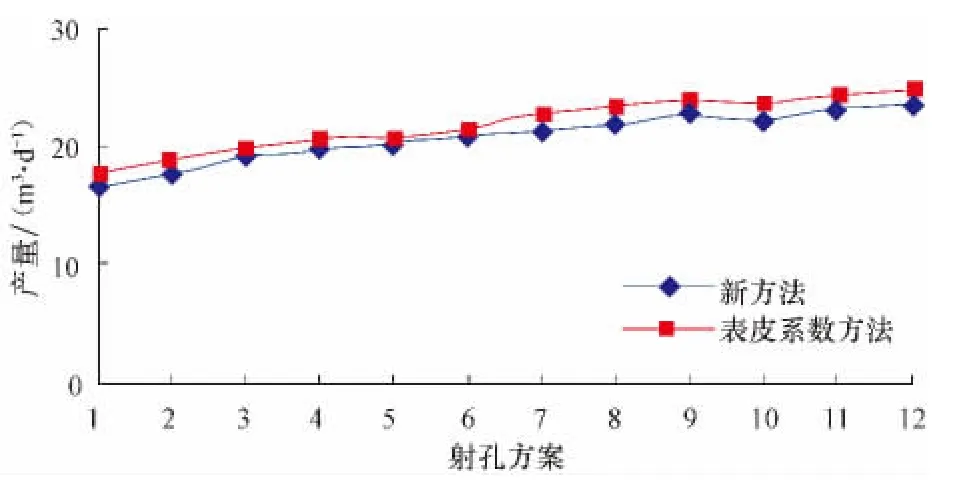
图13 新方法与表皮系数方法计算结果对比Fig.13 Comparison between the new method and the skin method

2）表皮系数法是在对问题进行简化处理的基础上、通过经验公式或数值模拟方法得到的，受认识程度和模拟精度的限制。新方法基于双径向流模型，采用等值渗流阻力法，充分考虑了以上各个因素的影响以及这些因素之间的相互影响，并且简化出的各部分流场之间没有重叠，更符合实际情况。

5 结 论

1）将McLeod射孔几何模型改进为双径向流模型，应用渗流力学原理和等值渗流阻力法，得到部分射开直井的产能计算方法。

2）参数敏感性分析认为，射开程度、射孔深度、射孔密度、压实程度对产能的影响很大，相位、孔径、压实带厚度对产能的影响很小，产能对各参数的敏感性在未射穿污染带时比射穿污染带时高。

3）产能与射孔深度、射孔密度、孔径、相位、压实带厚度、压实程度、射开程度之间均为非线性关系，工程设计时应尽量增大射孔深度、射孔密度、射开厚度，并避免压实损害程度过高。

4）计算实例表明，新方法的计算结果与表皮系数法相差5%左右。

5）在新方法的基础上，研究各射孔参数之间的约束关系，可为射孔参数优化设计提供理论依据。

［1］王海东，孙新波.国内外射孔技术发展综述［J］.爆破器材，2006，35（3）：33－36.Wang Haidong，Sun Xinbo.Perforating technology development inside and outside of china［J］.Explosive Materials，2006，35（3）：33－36.

［2］姚约东，刘艳华.打开不完善井的合理产能评价［J］.石油钻探技术，2010，38（2）：14－18.Yao Yuedong，Liu Yanhua.Productivity evaluations of partial penetrating wells［J］.Petroleum Drilling Techniques，2010，38（2）：14－18.

［3］张丽华.射孔参数对油井产能影响的分析［J］.石油大学学报：自然科学版，1993，17（2）：33－38.Zhang Lihua.Effect of perforation parameters on oil well productivity［J］.Journal of the University of Petroleum，China：E－dition of Natural Science，1993，17（2）：33－38.

［4］牛超群，张玉金.油气井完井射孔技术［M］.北京：石油工业出版社，1994：61－67.Niu Chaoqun，Zhang Yujin.Perforating technology of oil and gas well completion［M］.Beijing：Petroleum Industy Press，1994：61－67.

［5］Asadi M，Preston F W.Characterization of the crushed zone formed during jet perforation by qualitative scanning electron microscopy and quantitative image analysis［R］.SPE 22812，1991.

［6］Pucknell J K，Berhmann L A.An investigation of the damaged zone created by perforating［R］.SPE 22811，1991.

［7］牛华.试论射孔与油气井产能的关系［J］.大庆石油学院学报，1995，19（2）：32－34.Niu Hua.Discussion on the relationship of perforation and oilgas well production［J］.Journal of Daqing Petroleum Insititute，1995，19（2）：32－34.

［8］李东传，唐国海，孙新波，等.射孔压实带研究［J］.石油勘探与开发，2000，27（5）：112－114.Li Dongchuan，Tang Guohai，Sun Xinbo，et al.A study on perforation crushed－zone［J］.Petroleum Exploration and Development，2000，27（5）：112－114.

［9］Harris M H.The effect of perforating oil well productivity［J］.Journal of Petroleum Technology，1966，18（4）：518－528.

［10］Klotz J A，Krueger R F，Pye D S.Effect of perforation damage on well productivity［R］.SPE 4654，1974.

［11］McLeod H O，Jr.The effect of perforating conditions on well performance［R］.SPE 10649，1983.

［12］Karakas Metin，Tariq S M.Semianalytical productivity models for perforated completions［R］.SPE 21477，1990.

［13］唐愉拉，潘迎德.有限元方法在射孔完井中的应用［J］.石油学报，1989，10（3）：48－58.Tang Yula，Pan Yingde.Evaluation of perforating completion by finite element method［J］.Acta Petrolei Sinica，1989，10（3）：48－58.

［14］唐愉拉，潘迎德，冯跃平.油、气井射孔完井产能预测和优化射孔设计［J］.油气井测试，1991（2）：102－125，101.Tang Yula，Pan Yingde，Feng Yueping.Productivity forecast and optimal design of the perforated oil and gas well［J］.Well Testing，1991（2）：102－125，101.

［15］郎兆新，张丽华，朱九成，等.射孔工程应用软件WPSYS－A的开发［J］.石油大学学报：自然科学版，1992，16（6）：42－48.Lang Zhaoxin，Zhang Lihua，Zhu Jiucheng，et al.Development of well perforation engineering software WPSYS－A［J］.Journal of the University of Petroleum，China：Edition of Natural Science，1992，16（6）：42－48.

［16］李祥贵，王清河，李元.射孔完井模型的数值模拟［J］.石油大学学报：自然科学版，1996，20（2）：48－53.Li Xianggui，Wang Qinghe，Li Yuan.Numerical simulation model of perforated well completions［J］.Journal of the University of Petroleum，China：Edition of Natural Science，1996，20（2）：48－53.

［17］成绥民，王天顺.表皮系数系统分解方法［J］.油气井测试，1992（1）：35－40.Cheng Suimin，Wang Tianshun.The system decomposition method of the skin factor［J］.Well Testing，1992（1）：35－40.

［18］张红霞.表皮系数系统分解研究与应用［D］.青岛：中国石油大学（华东）石油工程学院，2006：8－12.Zhang Hongxia.The system decomposition research and application of the skin factor［D］.Qingdao：China University of Petroleum（Huadong），School of Petroleum Engineering，2006：8－12.

［19］张建国，杜殿发，侯健，等.油气层渗流力学［M］.2版.东营：中国石油大学出版社，2009：126－133.Zhang Jianguo，Du Dianfa，Hou Jian，et al.Seepage mechanics of reservoir［M］.2nd ed.Dongying：China University of Petroleum Press，2009：126－133.

［20］Joshi S D.A review of horizontal well anddrainhole technology［R］.SPE 16868，1987.

［21］陈元千，邹存友.考虑各向异性和偏心距影响的水平井产量公式推导、对比与应用 ［J］.新疆石油地质，2009，30（4）：486－489.Chen Yuanqian，Zou Cunyou.Derivation，comparison and application of horizontal well production formula considering anisotropy and eccentricity effects［J］.Xinjiang Petroleum Geology，2009，30（4）：486－489.

［22］葛家理，刘月田，姚约东.现代油藏渗流力学原理：下［M］.北京：石油工业出版社，2003：29－51.Ge Jiali，Liu Yuetian，Yao Yuedong.Seepage mechanics principle of reservoir in modern：partⅡ［M］.Beijing：Petroleum Industy Press，2003：29－51.

［23］Besson J.Performance of slanted and horizontal wells on an anisotropic medium［R］.SPE 20965，1990.