古塔变形参数的分析

张明会

(陇南师范高等专科学校 数学系，甘肃 成县 742500)

1 问题的提出和复述

建筑物(尤其是古代建筑物和高层建筑物)，由于长时间承受自重压力、气温变化、风力影响、雨水侵蚀等作用，偶然还要受地震、飓风等自然因素和爆炸、火灾等非自然因素的影响，都会产生各种变形，诸如倾斜、弯曲、扭曲等。为保护古代建筑——古塔，文物部门需适时对古塔进行观测，了解各种变形量，以制定必要的保护措施。

若某古塔已有上千年历史，是我国重点保护文物。管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测。据附件1提供了这4次观测的数据。请根据这些数据，建立数学模型讨论以下问题。

1.1给出确定古塔各层中心位置的通用方法，并列表给出各次测量的古塔各层中心坐标。

1.2分析该塔倾斜、弯曲、扭曲等变形情况。

1.3分析该塔的变形趋势。

2 模型的假设

为了简化模型，便于讨论和计算，现对模型做一些合理的假设。

2.1古塔在修建时没有任何方向的倾斜，即古塔的中心曲线与地面垂直；

2.2 古塔的任何一个平行于地面的横截面都是正多边形(或圆形)；

2.3 古塔的每一层都接近于一个正棱柱(或圆柱)；

2.4 在四次测量时，每层塔的相同序号的点是相同的，即同序同点；

2.4 每次测量时都在每层塔的下底面和上底面相对应的地方上选点。

3 符号说明与名词的定义

为方便叙述和讨论，现对文中所用的符号、变量和名词做如下的说明与定义。

3.1 重要符号的名称和意义。

Kα表示曲线的倾斜度，α表示曲线的倾斜角；

Kβ表示曲线的弯曲度，β表示曲线的弯曲角；

Kγ表示曲线的扭转度，γ表示曲线的扭转角；

|v|表示向量v的模；

∑Y表示对向量Y求和，即∑Y=Y1+Y2+…+Yn.

3.2相关概念及其定义。

为了便于使用矩阵表示和计算曲线、平面图形、空间图形的相关问题，现引入系列定义。

3.2.1 曲线和图形的矩阵表示。

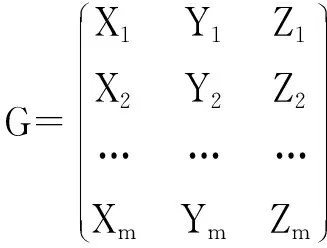
定义1 设曲线C上有n个点，其坐标分别为A1(x1,y1,z1),A2(x2,y2,z2),…,An(xn,yn,zn),则矩阵

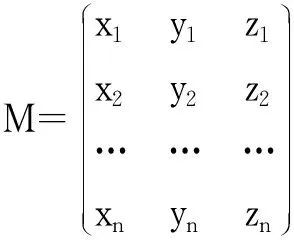
下文中如无特殊说明，曲线和它的坐标将不再区分，即曲线C也称为曲线M。

定义2 设多边形AB…K的顶点坐标依次为A(x1,y1,z1),B(x2,y2,z2),…,K(xk,yk,zk),则矩阵

有了以上的定义，曲线和多边形就可以用矩阵表示了，为数据的处理带来了方便。

3.2.2 正多边形中心的定义、性质和计算。

定义3 设有正多边形AB…N，其外接圆的圆心P称为正多边形AB…N的中心。

需要注意的是，非正多边形不能这样定义中心，但可以定义中心曲线，这个问题见后面讨论。

对于正多边形的中心，有如下的性质

性质1 设P是正多边形AB…N的中心，则必有

(1)

性质2 设正多边形A1A2…A2n是一个正2n边形，P是它的中心，则有

(2)

根据定义和性质1，性质2对于正多边形的中心坐标就有如下的计算方法。

定理1 设正多边形AB…N的坐标为

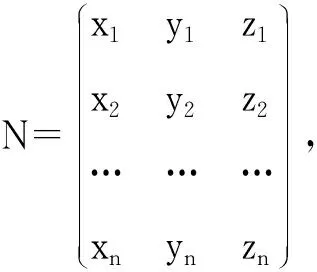
(3)

公式3 称为正多边形中心坐标公式。

定理2 设正多边形AB…N的坐标为

(4)

利用公式4，当已知正多边形的n-1个坐标和中心坐标时就可以求出另外任意一个点的坐标，因此公式4称为余点坐标公式。

3.2.3 非正多边形中心曲线的定义和坐标计算。

定义4 设多边形A1A2…An由两个正多边形

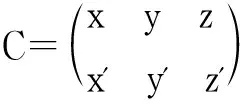
图1 中心曲线

对于由多个正多边形连接成的非多边形同样可以定义中心曲线。

仿照多边形中心的处理，我们可以定义空间多面体的中心和中心曲线。

3.2.4 正面体中心的定义、性质和计算。

定义5 设有空间正多面体AB…N，其外接球的球心P称为正多面体AB…N的中心。

对于正多面体中心的性质和计算方法与正多边形相似，公式1, 公式2, 公式3, 公式4也成立，不再赘述。

对于非正多面体中心曲线的定义与非正多边形相似。

3.2.5 曲线倾斜度、弯曲度的定义及计算。

定义6 设曲线C的起点为A，终点为B，则直线AB的倾斜角α称为曲线C的倾斜角，直线AB的斜率k称为曲线C的斜率。为了避免与直线的斜率相混淆，这里将曲线的斜率称为曲线的倾斜度，记为Kα．

如图2，若A(x1,y1,z1),B(x2,y2,z2)是曲线C的起点和终点，则由倾斜度的定义就有

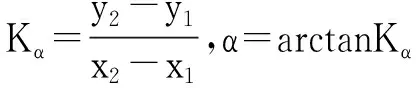
(5)

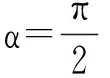
图2 曲线的倾斜度和弯曲度

根据以上的定义，弯曲度有如下的计算公式，如图2

设A1(x1,y1z1),A2(x2,y2,z2),A(n-1)(x(n-1),y(n-1),z(n-1)),An(xn,yn,zn),则

(6)

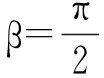
3.2.6 图形扭转度的定义及计算。

图形的扭转度是一个图形或具有对应性质的两个图形的旋转程度的指标，旋转的角度越大扭转度就越大。

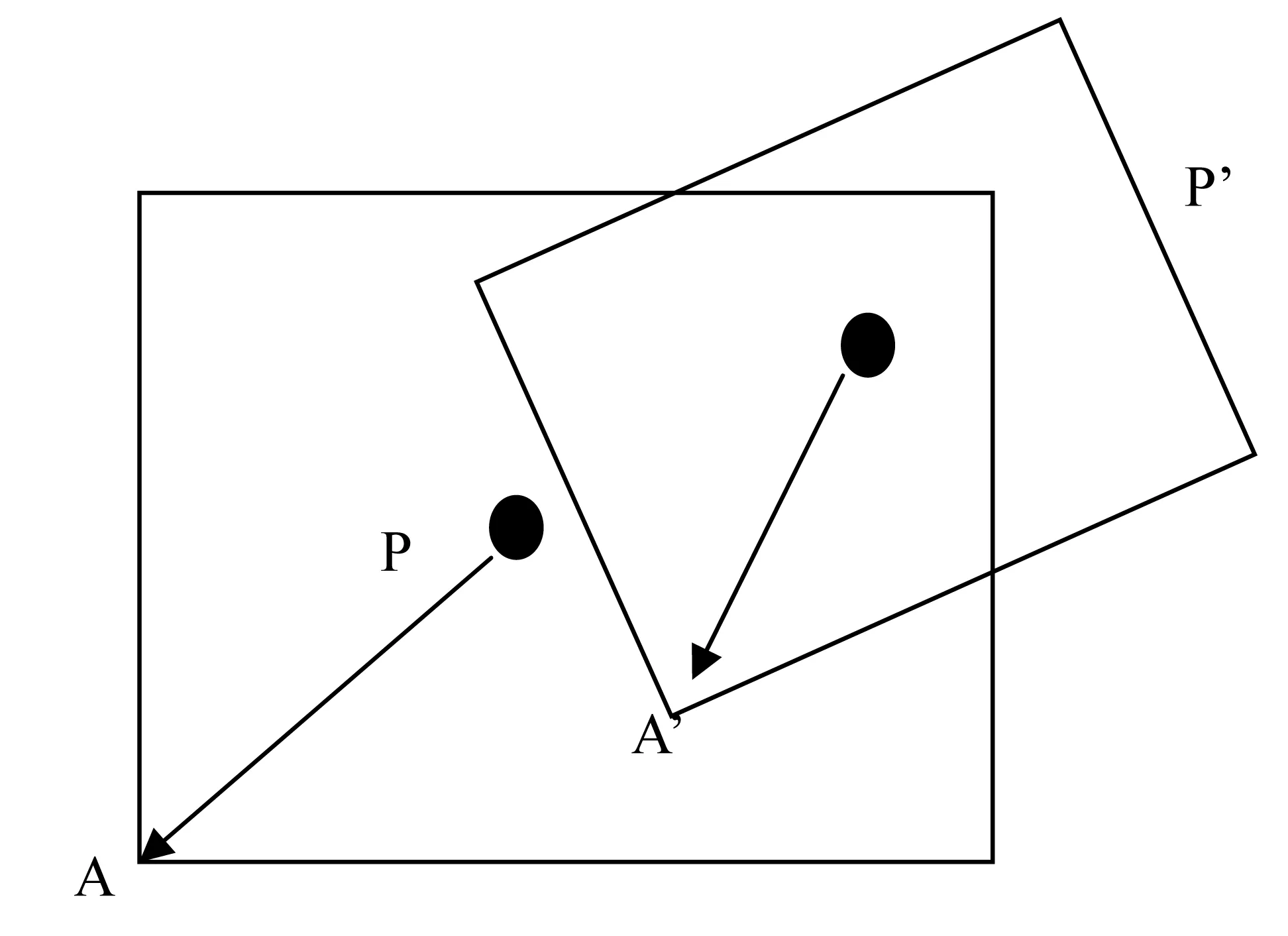
图3 扭转度

根据扭转度的定义，扭转度有如下的计算公式

如图3，设A(x1,y1,z1),P(x,y,z),A'(x1',y1',z1'),P'(x',y',z'),则

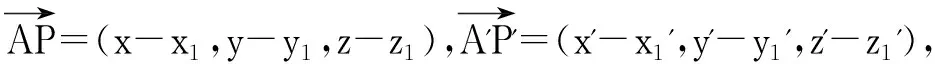
(7)

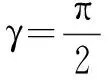
4 模型的建立

在以上讨论的基础上，现对古塔的中心位置、倾斜度、弯曲度和扭转度及其夹角的问题进行处理。

4.1 古塔各层中心位置的确定。

由假设2，即古塔的截面是正多边形，现将1986年对第一层观测的数据利用MathCAD软件做出图形，如图4，可以看出其截面确实接近正八边形，就是说假设是合理的和可以利用的。

图4 古塔截面图

从而就有

上式表明该层古塔的中心就是它的上下底面对应坐标的代数平均数，也就是说对于一层古塔，只要知道它的上下底面的坐标就可以完全确定它的中心的坐标

(8)

下面利用中心曲线讨论古塔的倾斜、弯曲和扭转等变形问题。

4.2 古塔倾斜度和倾斜角的确定。

(9)

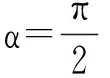
4.3 古塔弯曲度和弯曲角的确定。

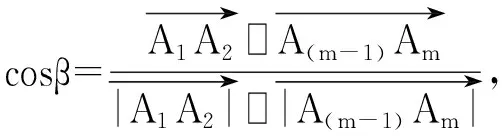
(10)

4.4 古塔扭转度和扭转角的确定。

由定义8，于古塔的扭转度和扭转角就是其最下层和最上层多边形的扭转度和扭转角，因此由公式7，就有

(11)

5 模型的评价与改进

该模型通过定义中心曲线和倾斜度、弯曲度、扭转度等概念，结合四次观测数据，利用MathCAD软件计算，给出了确定古塔中心曲线的通用方法，并在此基础上计算了该古塔的中心曲线、倾斜度、弯曲度、扭转度等衡量变形的指标。

模型结构简单，计算方便，易于理解和应用，模型的结果不仅对于古代建筑安全性的评价有指导意义，而且对于现代建筑(尤其是高层建筑)的安全评估也有一定的参考价值。是一个简单而实用的模型。

然而模型中也存在一些不足：

5.1没有考虑每层观测点在同一平面内的情况；

5.2将各层塔体看成柱体；

5.3舍弃了部分残缺数据等。

这些因素对模型的精确度都有一定的影响，在实际使用时要加以考虑，以提高模型的精确度。

以上不足之处将在以后的研究中继续探讨和完善。

[1]复旦大学数学系. 数学分析[M]. 北京：高等教育出版社，2001.

[2]张禾瑞.高等代数[M]. 北京：高等教育出版社，1997.

[3]袁长迎.掌握和精通Mathcad2000[M]. 北京：机械工业出版社，2001.

[4]冯杰，王勤，等.数学建模原理与案例[M].北京：科学出版社，2007.