正方形五芯光子晶体光纤的耦合特性分析

钱 燕，刘 敏，杨 静，马云华

(重庆大学通信工程学院，重庆400044)

引 言

光子晶体光纤由于其无尽的单模传输、可控的非线性、灵活的色散及大模面积［1-5］等特性而成为近年来研究的热点。其中多芯光子晶体光纤(photonic crystal fiber，PCF)因具有更大的模场面积和更新颖的导光特性而在很多光学器件中有着重要的运用，如光纤定向耦合器［6］、矢量传感器［7］、光纤激光器［8］等。目前对多芯PCF特性的理论研究主要包括双芯 PCF 的耦合特性［9］、模间色散特性［10］、高双折射特性［11］以及三芯、四芯光纤的非线性特性［12-13］等，与三芯、四芯PCF相比，五芯PCF具有更大的模面积，更有望获得高功率、高光速质量的激光输出。多芯PCF纤芯间的耦合特性对相位锁定［14］具有决定作用，是设计多芯PCF波分复用器和定向耦合器的理论依据，目前鲜有报道基于正方形晶格排列的五芯光子晶体光纤的耦合特性的研究。作者由五芯PCF 5个超模的特性研究模式和耦合特性之间的关系，利用有限元法详细分析了五芯PCF结构参量对耦合特性的影响，为设计基于多芯PCF的光学器件提供理论依据。

1 理论模型

基于正方形排列的五芯光子晶体光纤的横截面结构如图1a所示，空气孔采用正方形排列，纤芯1和距离中心3Λ位置的纤芯2、纤芯3、纤芯4、纤芯5通过填充高折射率材料形成纤芯。其结构参量为:纤芯折射率 n1=1.46，背景折射率 n2=1.45，空气孔的折射率n3=1，空气孔间距Λ=2.6μm，空气孔直径为d，占空比d/Λ，纤芯直径D=3μm，此时归一化频率ν＜π，每个纤芯保证单模传输［15］。图1b所示为5个纤芯在波长λ=1.55μm时的同相位模场分布图，可以看出各纤芯中的模场只是强度不同，并没有改变其单模输出特性。

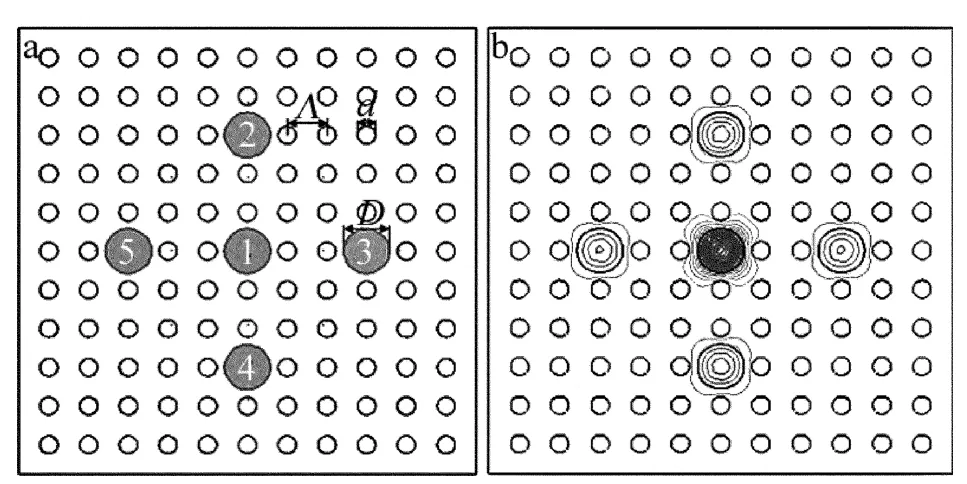
Fig.1 a—cross-section of five-core photonic crystal fiber b—in-phase mode field distribution

利用有限元法求得五芯PCF各超模的电场矢量分布图如图2a～图2e所示，依次为第一超模到第五超模，由图2可知，第一超模与第五超模分别为反对称模和对称模，且除了第一超模和第五超模外，其余超模纤芯1中电场矢量为0，因而对于纤芯1而言，超模1和超模5在传播方向上发生周期性的相加和相减，导致中间纤芯和外围4个纤芯之间的场功率进行周期性交换。利用双芯PCF耦合长度的计算方法［16］来求解五芯PCF的耦合长度，此处耦合长度即为中间纤芯能量完全转移到外围纤芯时所传播的距离，从模式理论角度来说，即为对称模和反对称模产生“差拍”的一半，对应为第一超模和第五超模产生“差拍”长度的一半，因而对于五芯PCF而言，其耦合长度的计算方法为:

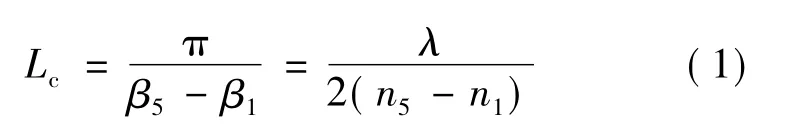
式中，n5，n1表示第五超模和第一超模对应的有效折射率，λ是传输光波长，β5和β1表示第五超模和第一超模对应的传播常数。

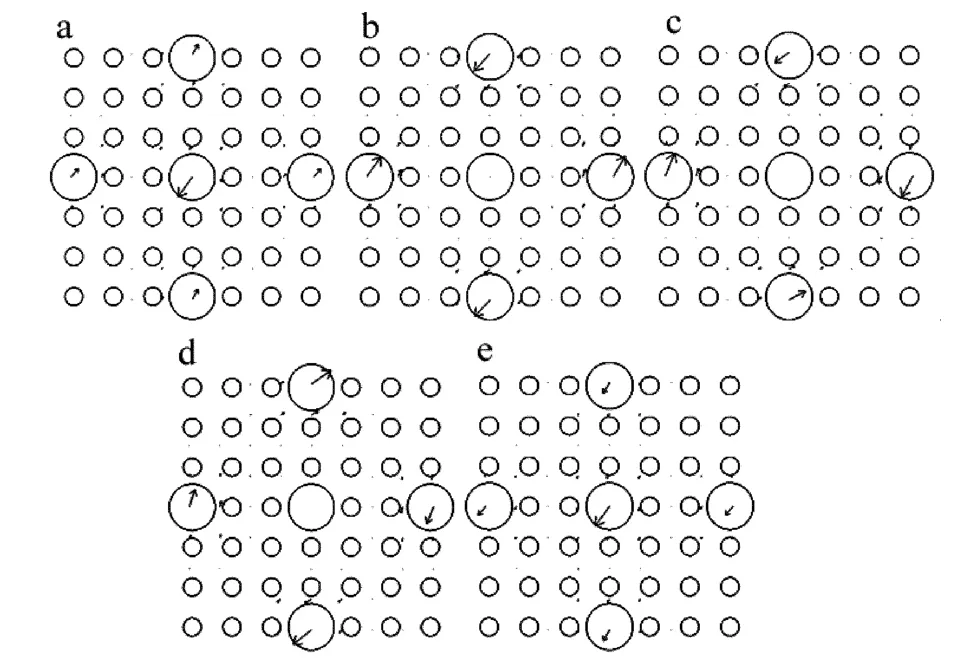
Fig.2 Distribution of the electric field vector

2 耦合特性分析

基于上述求解耦合长度的方法，在结构参量分别为 Λ=2.6μm，d/Λ=0.45，n1=1.46，D=3μm，λ=1.55μm时，通过有限元法求得超模的有效折射率n1=1.441055，n5=1.441157，代入(1)式中得到Lc=7598μm。在相同的参量结构下，通过光速传播法得到的模场分布随传输距离的变化如图3所示。图3a为光从中间纤芯1入射时的模场分布，图3b为经过传输长度L=7357μm时各纤芯的模场分布。由图3b可知，由于周围4个纤芯对称分布，纤芯1中的能量平均分配到周围4个纤芯中，在传输长度L=7357μm时，中间纤芯1中功率由极大值降至极小值，此长度与给出的计算耦合长度求得的耦合长度7598μm比较，两者耦合长度误差为4.45%，研究表明该误差为系统误差，跟计算选取的网格和步长有关。

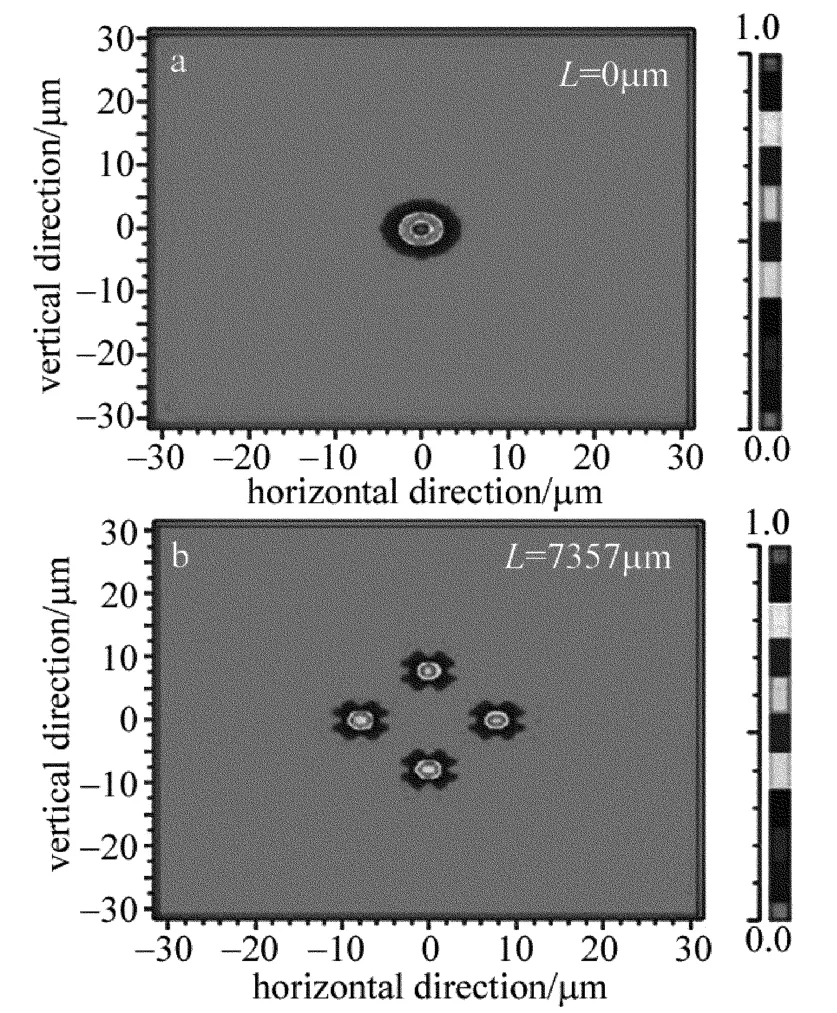
Fig.3 Modefield distributions atλ=1.55μm

由导波光学理论可知，光纤结构和传播波长的改变将导致模场面积和模场分布的变化，从而引起耦合长度Lc的变化。图4为纤芯折射率为n1=1.46、空气孔占空比d/Λ=0.45、纤芯直径 D=3μm、孔间距Λ从2.4μm变化到2.8μm时，耦合长度Lc随波长的变化曲线。由图4可以看出，随着传播波长λ0的增加，耦合长度Lc逐渐减小。这是因为光波在纤芯表面发生全内反射，透射波的衰减系数α［17］可以表示为:α=2π(n12sin2θ1-n22)1/2/λ0，其中λ0代表光在真空中的波长，n1为纤芯的折射率，n2为包层的折射率。由α的计算公式可以看出，当波长λ0增加时，衰减系数α减小，光波从纤芯1中透射到周围4个纤芯时更容易，耦合长度变短。同时在传输波长λ0一定时，耦合长度Lc随着Λ的增大而增大，这是因为纤芯间距的增大将引起相邻两纤芯间模场有效交叠面积的减小，从而导致纤芯间的耦合作用减弱，耦合长度增加。

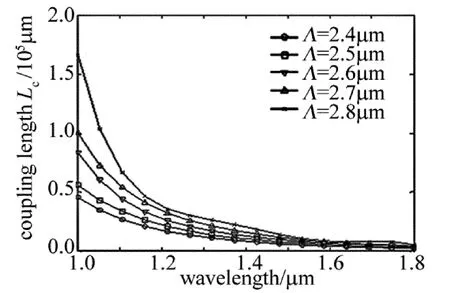
Fig.4 Coupling length Lc as a function of wavelength and core-to-core distance

图5 为纤芯折射率为 n1=1.46、孔间距 Λ=2.6μm、纤芯直径D=3μm、占空比 d/Λ 从 0.35变化到0.55时，耦合长度Lc随占空比的变化情况。由图可知，当占空比d/Λ增加时，耦合长度Lc增加，这主要是由于占空比增加时，纤芯对光的束缚能力增强，模场面积减小，纤芯间耦合效应变弱，导致耦合长度增加。在1.55μm传输波长处，占空比d/Λ=0.35和d/Λ=0.55时，耦合长度分别为 2980μm，23484μm，耦合长度明显增加，因此可以通过减小占空比来减小耦合长度。

Fig.5 Coupling length Lc as a function of air-filling ratio

图6 所示为孔间距Λ=2.6μm、纤芯直径D=3μm、占空 d/Λ=0.45、纤芯折射率 n1从 1.45 变化到1.47时，耦合长度Lc随纤芯折射率的变化曲线。由图6可知，耦合长度Lc随着纤芯折射率n1的增加而增加，导致这一变化趋势的原因是当纤芯折射率n1增加时，透射波的衰减系数α也会增大，导致倏逝波在纤芯间的渗透变得更加困难，耦合长度增加。从6图中可以看出在波长1.0μm～1.6μm范围内，耦合长度差异较大，但在1.6μm～1.8μm范围内，耦合长度差异较小，这一结果表明，随着波长的增加，纤芯折射率对耦合长度的影响减小。

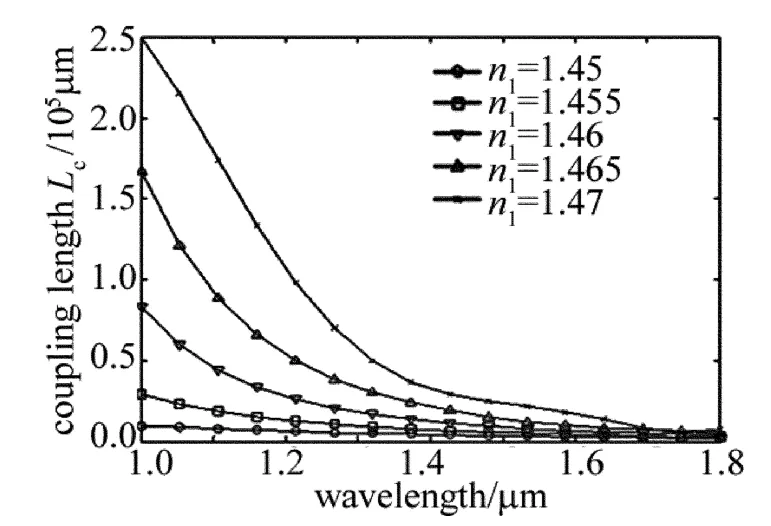
Fig.6 Coupling length Lc as a function of core refractive index

图7 为孔间距 Λ=2.6μm、纤芯折射率 n1=1.46、占空比d/Λ=0.45、纤芯直径 D 从 2.0μm 变化到3.5μm时，耦合长度Lc随纤芯直径的变化曲线。由图7可知，当纤芯直径增加时，耦合长度Lc增加。这主要是因为当纤芯直径增加时，虽然模面积有所增加，但各纤芯对光的束缚能力更强，最终在两者的共同作用下导致纤芯之间耦合效应减弱，耦合长度增加。在通信窗口1.31μm和1.55μm处，耦合长度Lc随纤芯直径变化比较明显，因而可以通过调节纤芯直径来满足特定耦合长度的要求。

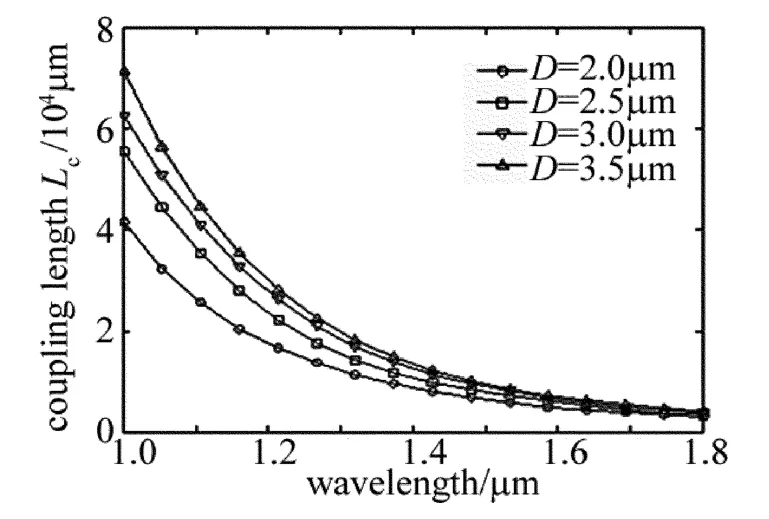
Fig.7 Coupling length Lc as a function of core diameter

3 结论

根据5个超模的电场矢量图研究模式和耦合特性之间的内在联系，通过超模有效折射率求解耦合长度，与光速传播法计算结果比较，两者展现了很好的一致性。对于五芯PCF而言，孔间距Λ、占空比d/Λ、纤芯折射率n1以及纤芯直径D的增加都将导致纤芯对光束缚能力增加，模场的交叠面积减小，消逝波在纤芯之间的渗透变得更加困难，因而导致耦合长度Lc增加。而对于结构一定的五芯PCF而言，随着波长的增加，光的渗透能力增强，纤芯之间耦合变得更加容易，最终耦合长度Lc减小，这些结论对设计用于通信的多芯光纤的波分复用器以及定向耦合器具有一定的参考价值。

［1］SAITOH K，KOSHIBAM.Numericalmodeling of photonic crystal fibers［J］.Journal of Lightwave Technology，2005，23(11):3580-3590.

［2］JAN D，LIU M，HE D，et al.Research of photonic crystal fiber with high nonlinear flattened dispersion property［J］.Laser Technology，2013，37(2):187-190(in Chinese).

［3］LIAO Zh Y，LIU M，QIAN Y，et al.Octagonal dispersion compensation fiber［J］.Laser Technology，2013，37(4):506-510(in Chinese).

［4］LING F，GAN X S，GU M.Nonlinear opticalmicroscope based on double-clad photonic crystal fibers［J］.Optics Express，2005，13(14):5528-5534.

［5］LIMPERT J，SCHREIBER T，NOLTE S，et al.High-power airclad large-mode-area photonic crystal fiber laser［J］.Optics Express，2003，11(7):818-823.

［6］BERGH R A，KOTLER G，SHAW H J.Single-mode fibre optic directional coupler［J］.Electronics Letters，1980，16(7):260-261.

［7］YANG S.Directional pattern of a cross vector sensor array ［J］.The Journal of the Acoustical Society of America，2012，131(4):3484-3489.

［8］WADSWORTH W，PERCIVAL R，BOUWMANSG，et al.High power air-clad photonic crystal fibre laser［J］.Optics Express，2003，11(1):48-53.

［9］LIU M，CHIANG K S.Propagationof ultrashortpulsesin a nonlinear two-core photonic crystal fiber［J］.Applied Physics，2010，B98(4):815-820.

［10］LIU M，CHIANG K S.Two-core photonic crystal fiber with zero intermodal dispersion［J］.Optics Communications，2012，293(15):49-53.

［11］LID，LIU M，JIAN D，et al.Study on characteristics of highly birefringent dual-core photonic crystal fibers［J］.Chinese Journal of Lasers，2012，39(4):106-110(in Chinese).

［12］LIU M，CHIANG K S.Nonlinear switching of ultrashort pulses in multicore fibers［J］.Quantum Electronics，2011，47(12):1499-1505(in Chinese).

［13］YICh Sh，ZHANG PQ，DAISh X，et al.Research progress of large-mode area photonic crystal fibers［J］.Laser ＆ Optoelectronics Progress，2012(10):1-11(in Chinese).

［14］CHEO P K，KINGGG，HUO Y.Recent advances in high-power and high-energy multicore fiber lasers［J］.Proceedings of the SPIE，2004，5335:106-115.

［15］FANG X H，CHAI L，HU M L，et al.Numerical analysis for structure optimization of seven-core photonic crystal fibers［J］.Acta Physica Sinica，2009，58(4):2495-2500(in Chinese).

［16］MA L F，LIU M，LID，et al.A kind of hollow dual-core photonic crystal fiber with zero inter-modal dispersion［J］.Chinese Journal of Lasers，2012，39(8):129-134(in Chinese).

［17］GENG PCh.Research on seven-core and bandgap Yb-doped photonic crystal fibers［D］.Qinhuangdao:Yanshan University，2010:21-25(in Chinese).