改进小波包的滚动轴承故障诊断

任学平，庞 震，邢义通，辛向志

(内蒙古科技大学机械工程学院，内蒙古包头014010)

0 引言

被称之为“机械关节”的滚动轴承是机械设备不可缺少的基础件，对整个机械系统的正常运行起到关键性作用。由于其故障振动信号往往表现为非平稳特征，并且故障特征信息非常弱小，而机械在运转时产生的背景噪声常常很大，故障特征信息一般淹没在噪声中不易被识别出来。如何提取轴承故障特征信息并对其分析出来，是轴承故障诊断的关键技术[1-2］。

经验模态分解(EMD)可将信号分解至不同频段，是一种自适应的信号分解方法。在实际测得的滚动轴承振动信号中，经验模态分解往往含有较多噪声，对齿轮箱振动信号的分析带来不利影响[3-4］。小波分析是一种常用的非平稳信号处理方法，在非平稳信号去噪中具有一定的优势[5-6］。

由于小波包和EMD各有其优缺点，利用两者的结合来提取故障，小波去噪对故障信号作预处理，使信号分解精确度提高[2-3］。但子带信号会出现虚假频率成分，造成严重的频率混叠现象。在此提出改进小波包降噪与EMD分解信号，可以得到更为精确的故障信息。

1 基本理论

1.1 改进小波包

在小波包分解时，小波滤波器进行隔点采样，采样频率的减半往往会引起频率折叠;在波包重构过程中的隔点插零使得采样频率加倍，会产生无法滤去的真实频率映像，也就是虚假频率，对整个分解、重构过程造成频率混淆现象。因此，信号进行理想滤波就是防止分解过程中的频率折叠与去除重构中多余的虚假频率成分。基于此想法，在信号分解过程中，对经过滤波的频率进行快速傅里叶变换(FFT)，依据卷积滤波频带划分规律，将FFT后的低半频段或高半频段进行置零，再进行傅里叶逆变换(IFFT)处理，通过这3个步骤防止频谱发生交错(3个步骤用C与D来表示)，并避免了隔点采样引发的频率混叠。信号节点重构过程也做同样的处理(如图1所示)。图1中，G、H代表小波分解滤波器;g、h代表小波重构滤波器;↓2表示隔点采样;↑2表示隔点插零。

C和D的表达式分别为式(1)和式(2):

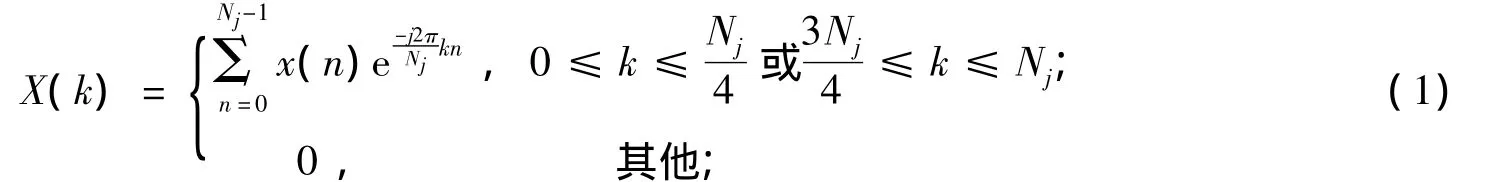
式中，x(n)表示小波变换第j层上的低频子带小波系数;Nj表示小波变换第j层分解信号的长度;k=0，1，…，Nj-1。

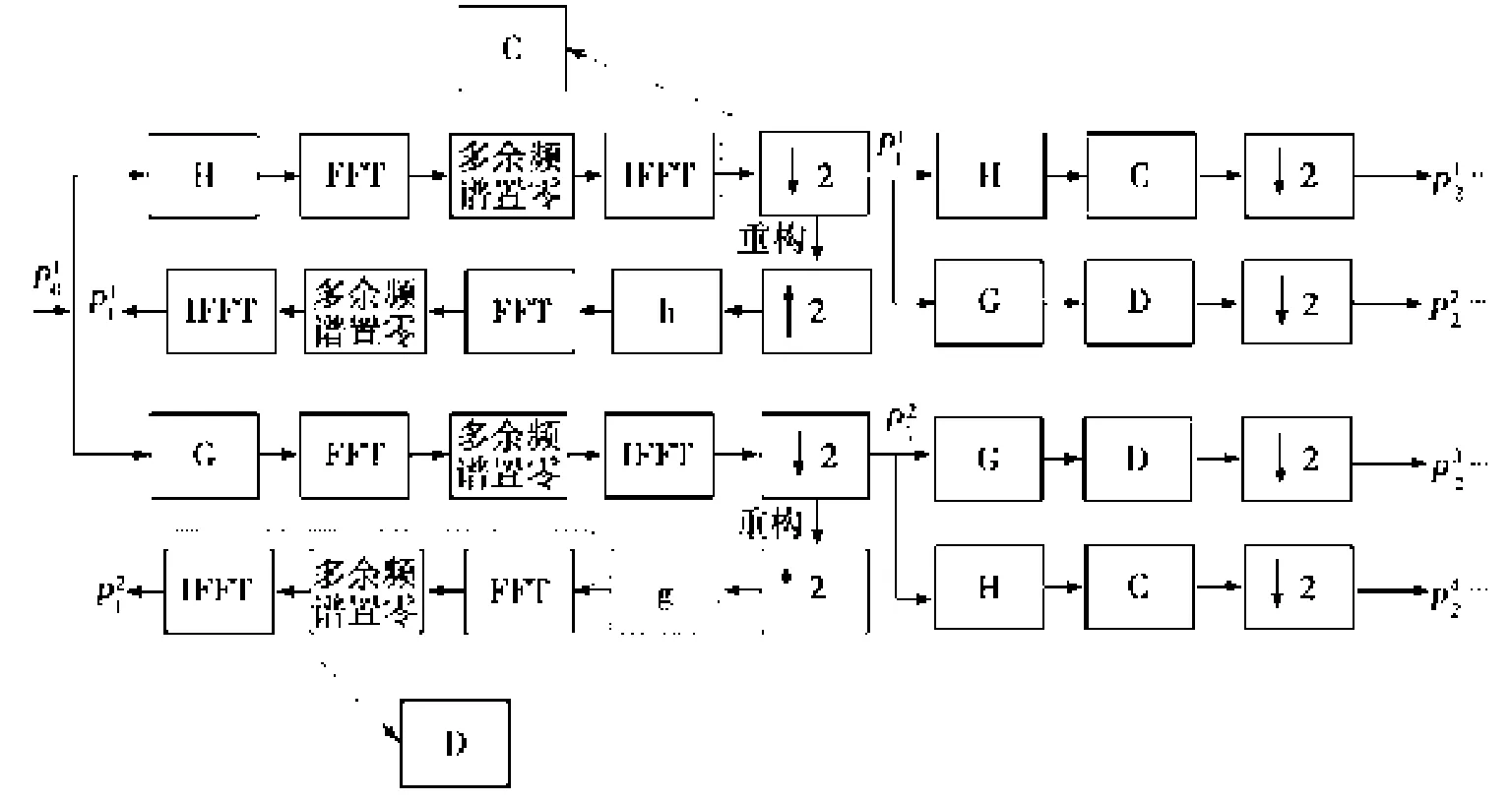
图1 改进小波包算法

由于小波包分解得到的各子带不是按照频率大小的顺序连续排列，而是无明显规律排列，本文采用改进滤波器组结构来解决此问题，其结构与原分解树的结构相同，都是二叉树结构，只是低通和高通滤波器的排列顺序发生了变化(如图2所示)，在每一级滤波器组中的第1个滤波器是LP，第2个滤波器是HP，然后从第2个滤波器开始，从上到下每两个滤波器类型进行一次变换。利用改进的滤波器组结构得到的频带划分是按频率大小顺序连续排列的均匀频带[7］。

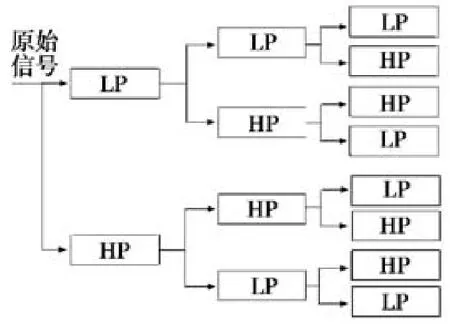
图2 调整的滤波器组

1.2 经验模态分解方法

EMD是把一复杂时间序列信号分解为不同时间尺寸特征的IMF分量之和[8］。每个分量需要达到两个条件:一是每一固有模态函数其极值点个数与过零点个数要相等或者相差不能超过1个;二是其上下包络线要以时间轴局部对称为准[9］。

1.3 仿真分析

为了验证改进小波包可以避免轴承虚假成份产生的有效性，现取具有实际故障特征仿真信号y(t)，y(t)的表达式为:

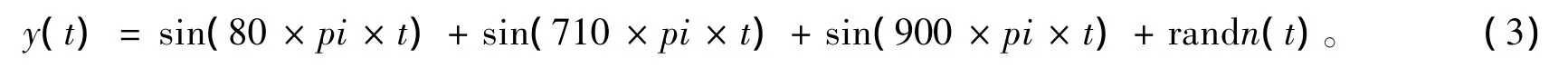
对含噪信号y(t)进行改进小波包处理，对其进行3层分解结果见图3。从图3中可以看出:子带频率顺序是从小到大排列，且从子带节点(3，0)、(3，5)、(3，7)中可以依次找到频率40 Hz、355 Hz、450 Hz。

而传统的小波包分解就产生了虚假频率成份，如图4所示。子带频率顺序排列杂乱，而且在子带节点(3，4)、(3，5)中不仅都产生了有用信号(450 Hz)，造成频率重叠，而且还都产生了无用信号(446 Hz)，导致虚假频率产生的现象。因此，改进小波包优于传统小波包。

2 改进小波包与EMD对轴承故障诊断

2.1 故障分析步骤

利用改进小波包和EMD对轴承故障信号的检测，可以按照以下步骤执行:

(Ⅰ)原始信号小波包分解层数的确定。

(Ⅱ)改进小波包分解。

(Ⅲ)提取属于故障频率范围的子带。

(Ⅳ)对提取信号进行EMD分解，求每个IMF与降噪后信号的互相关系数，并同时求出各个分量的峭度值[10-11］。

(Ⅴ)选择互相关系数与峭度值较大的IMF进行包络谱分析，提取故障信息。

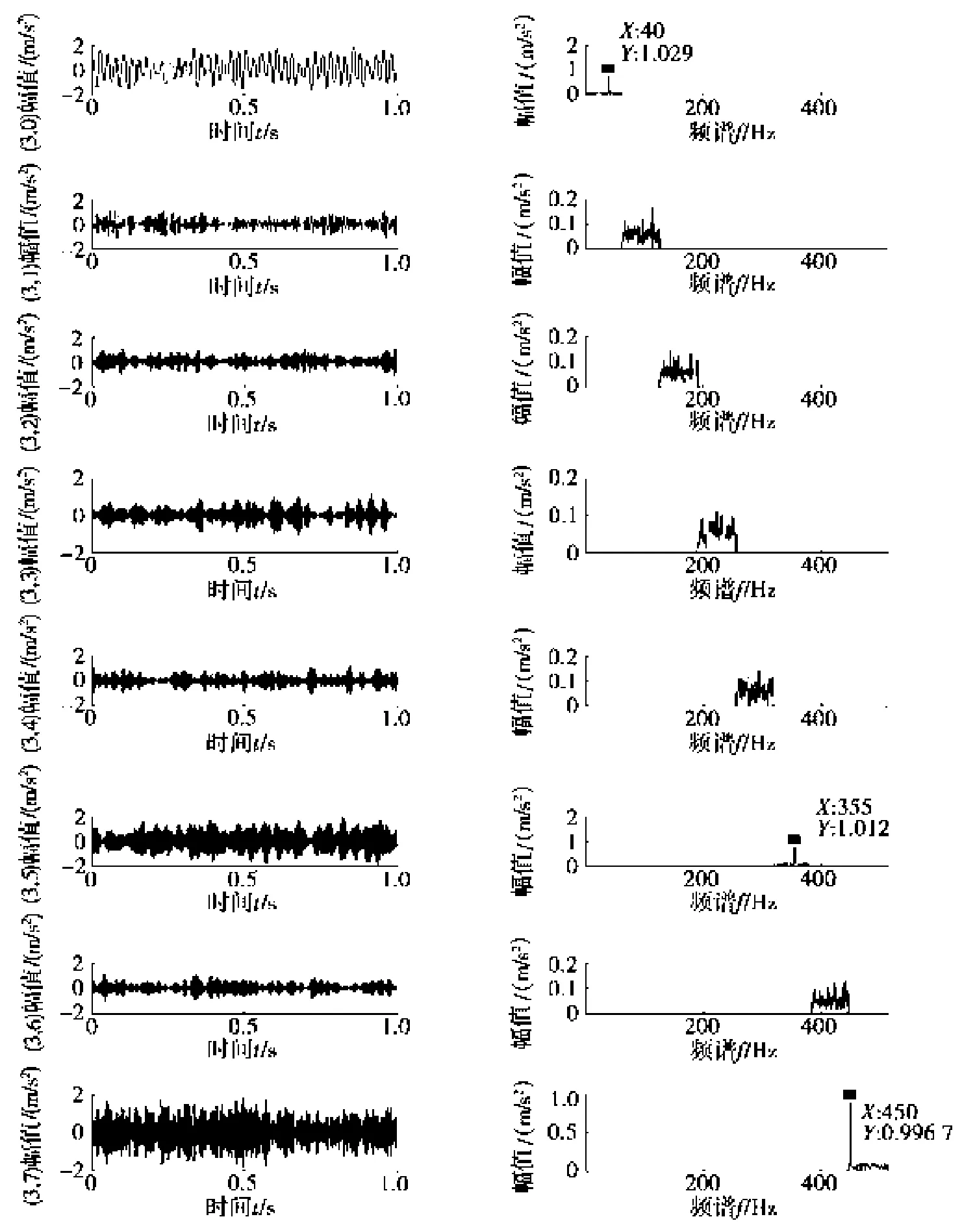
图3 改进小波包各节点结果及其频谱

2.2 实验分析

实验利用ZonicBook/618E测试系统测得一组机械轴承故障信号。轴承转速为1 350 r/min，采样频率为10 240 Hz，采样点N=2 048。轴承为N205EM圆柱滚子轴承，其外圈用线切割机切了一道宽0.1 mm，深0.2 mm平行轴承轴线方向的沟槽。轴承内径25 mm，外径52 mm，滚动体直径为7.5 mm，节圆直径为39 mm，滚动体数为12，接触角为0°。计算所得轴承各部件故障频率如表1所示。

图5为外圈故障信号，从图5中无法得到故障频率，依据前文故障分析步骤，首先确定分解层数，绝大多数滚动轴承故障分解层数取3～5层，本文在此采用5层小波包分解，可以得到更精确、范围更小的频率带，对振动信号(见图5a)进行快速傅里叶变换和快速傅里叶逆变换，对得到的各小波包子带信号进行处理，并调整滤波器组使子带频带顺序排列。

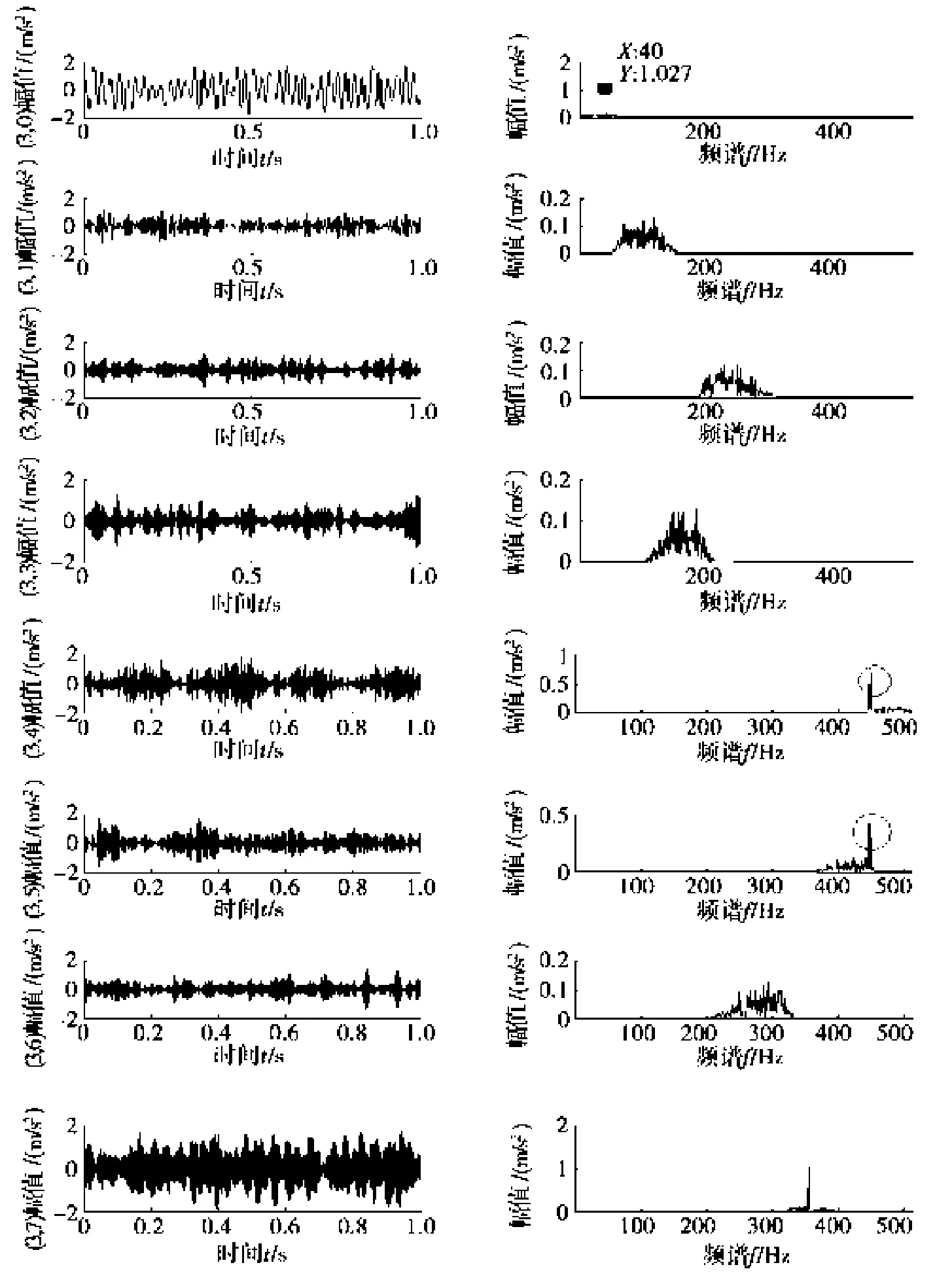
图4 传统小波包各节点结果及其频谱

表1 轴承各部件故障频率 Hz

图6为改进小波包子带信号。经计算，外圈故障应属于节点(5，0)内，图6a为节点(5，0)时域信号，从其功率谱(见图6b)中可以找到包含外圈故障频率110 Hz，但杂质信号依然很大，需要进一步分析。

图7为传统小波包对外圈故障分解得到节点(5，0)的信号，对比图6和图7可以发现:图7b中的频率比图6b中的频率多出了100 Hz、135 Hz、145 Hz信号，造成虚假频率的产生，不利于后续分析，所以，运用改进小波包分析信号。

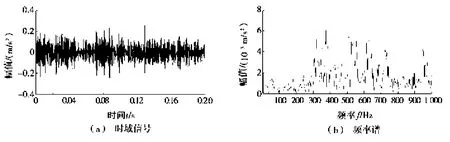
图5 轴承外圈故障信号图

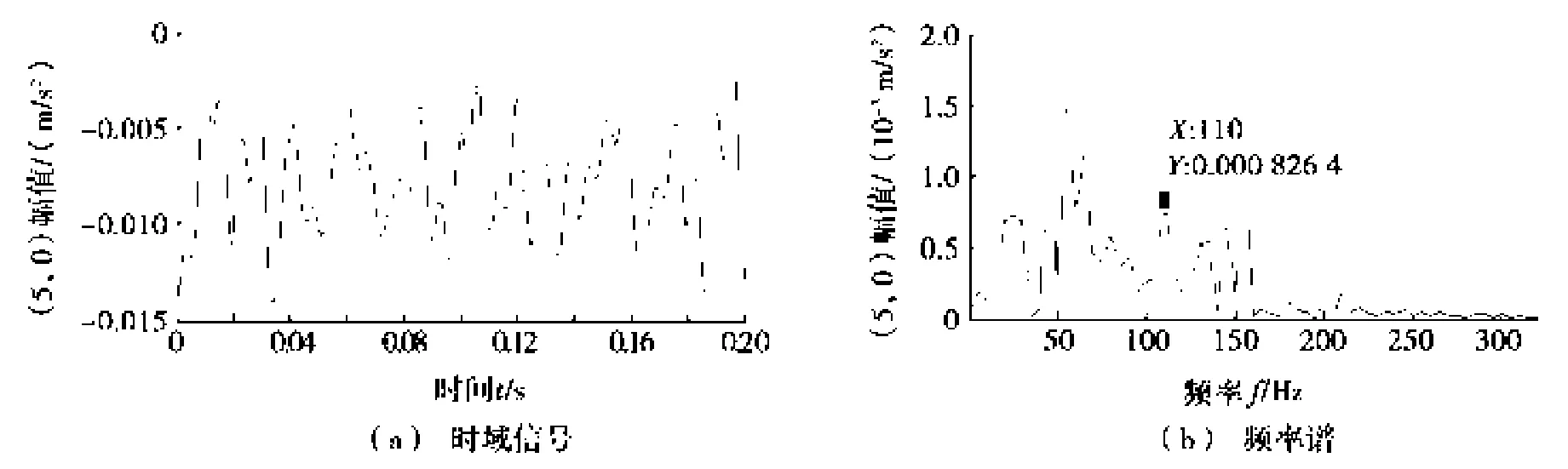
图6 改进小波包子带信号

图7 传统小波包子带信号

接着运用EMD分解图6a信号得到各分量IMF，对其进行相关系数、峭度准则比较(见表2)，发现IMF1和IMF2的相关系数都很大且大于0.1，峭度值都在3到8之间，满足故障数据要求。对IMF1和IMF2重构信号并进行包络谱分析得到图8，从图8中可以找到外圈故障频率为110 Hz，外圈故障频率与轴承转动频率之差为90 Hz。

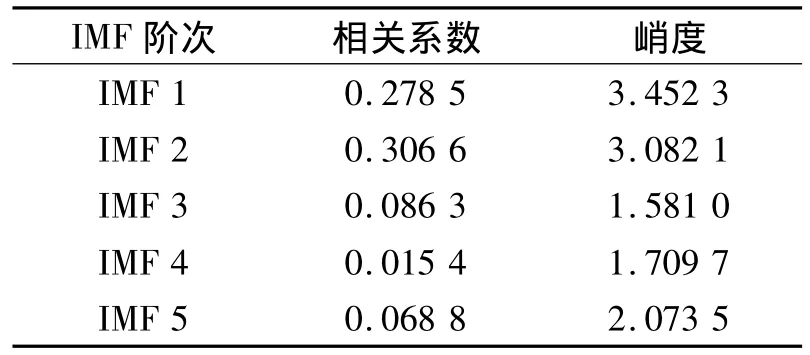
表2 IMF的相关性与峭度

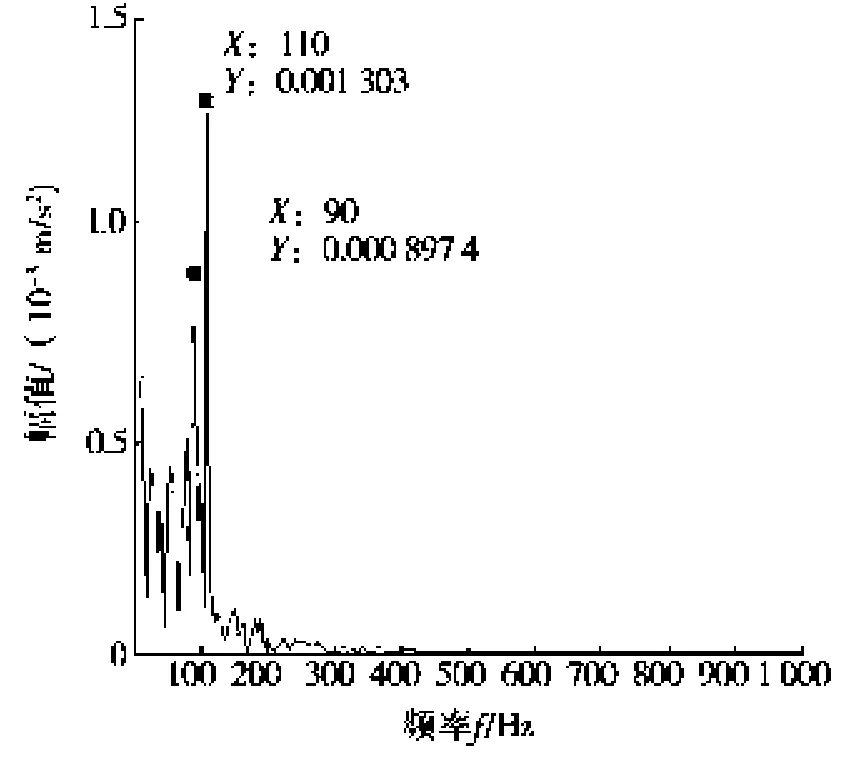
图8 重构信号的功率谱

3 结论

本文主要利用改进小波包和EMD相结合的方法来辨别轴承微弱故障信号。通过仿真与实例得出:该方法对轴承初期故障防止其产生虚假频率及频率混叠现象具有良好的效果，并准确地诊断出故障频率，有利于提高轴承故障诊断的准确性。

[1]杨国安.机械设备故障诊断实用技术[M］.北京:中国石化出版社，2007.

[2]夏均忠，刘远宏，冷永刚，等.微弱信号检测方法的现状分析[J］.噪声与振动控制，2011(3):156-161.

[3]夏均忠，苏涛，马宗坡，等.基于EMD的滚动轴承故障特征提取方法[J］.噪声与振动控制，2013(2):123-127.

[4]朱瑜，王殿，王海洋.基于EMD和信息熵的滚动轴承故障诊断[J］.轴承，2012(6):50-53.

[5]钟飞，郑晓斌，史铁林.基于小波神经网络的轴承未知异常诊断[J］.河南科技大学学报:自然科学版，2007，28(4):10-13.

[6]信思金，舒丹，梁磊，等.损伤识别系统中小波包信号特征量的提取[J］.河南科技大学学报:自然科学版，2006，27(2):29-32.

[7]薛蕙，杨仁刚，罗红.利用小波包变换实现电力系统谐波分析[J］.电网技术，2004，28(5):41-45.

[8]Huang N E.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Analysis[C］//Proc Roy Soc London.1998，A454:903-995.

[9]于德介，程军圣.EMD方法在齿轮故障诊断中的应用[J］.湖南大学学报，2002(6):48-51.

[10]苏文胜，王奉涛，张志新，等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J］.振动与冲击，2010，29(3):18-21.

[11]郭楠，潘宏侠，孙黎明.基于EMD细化包络谱分析在滚动轴承故障诊断中的应用[J］.煤矿机械，2010，31(2):206-208.