某微型车盘式制动器制动噪声分析

高昱斌，陈 燎，盘朝奉，杨 路

(1.江苏大学汽车与交通工程学院，江苏镇江212013;2.山东新大洋电动车有限公司，山东临沂276300)

0 引言

制动器的制动噪声一直以来都是研究的重点，产生制动噪声的机理至今没有达成共识。在几十年的研究过程中，形成了自激振动和“热点”两大理论。多数研究人员主要从几何特性耦合理论来探讨制动噪声问题，不仅考虑各部件的结构固有特性，还要考虑各部件之间的耦合关系[1-2］。清华大学的管迪华教授基于摩擦耦合理论提出了具有指导意义的能量馈入分析方法[3］。近年来一些学者提出了摩擦学理论[4］，主张研究制动噪声不应局限于动力学，也要从摩擦层的动态特性上进行深入研究。

目前，制动器制动噪声研究主要是利用有限元方法，利用弹簧单元来模拟摩擦接触，通过复特征值计算方法来预测可能出现的噪声频率，但是由于弹簧单元不能充分模拟摩擦接触的非线性，结果有很大的偏差。某微型车在制动到低速时前制动器容易出现制动尖叫，针对本问题建立制动盘、制动块、制动钳支架的有限元模型，基于非线性面接触的摩擦耦合理论进行部件的实模态分析以及系统的复模态分析。判定产生制动噪声的不稳定模态，找到各部件对不稳定模态影响最大的几阶模态，分析产生制动噪声的诱因，对制动器系统的结构和参数属性提出改进措施。

1 振动与噪声

声源振动在空气介质中产生波动—声波，继而传入人耳产生声觉。振动是噪声产生的根源，噪声强度级取决于振源表面振动速度的幅值，噪声的振动速度级与声压级关系为[5］:

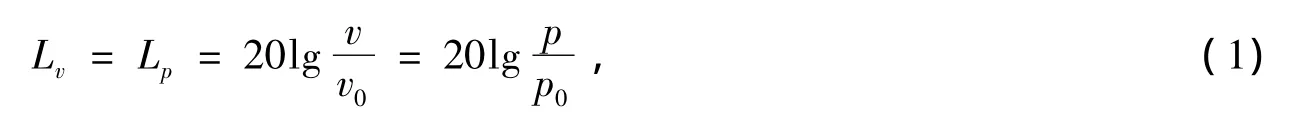
式中，Lv、Lp分别为振动速度级和声压级，dB;v为振动速度，m/s;p为声压，Pa;v0为基准振动速度，一般取v0=1.0×10-8m/s;p0为基准声压，p0=2.0×10-5Pa，是人耳对1 kHz空气声所能感觉到的最低声压。

由式(1)可以看出:已知振动速度后便可以判断这些振动产生的噪声级。制动过程中，系统产生的振动传递给空气进而产生了制动噪声。制动器在不稳定模态时的振动最为强烈，在制动时如果能避免不稳定模态的出现，就能降低制动噪声产生的可能。

盘式制动器的动力学方程可以表示为[6］:

式中，[M］、[C］和[Ks］分别为无摩擦制动器系统的质量矩阵、阻尼矩阵和刚度矩阵;[Kf］为制动盘和摩擦片接触面上的摩擦力导致的摩擦刚度矩阵;{x}为位移向量矩阵。

[Kf］是非对称矩阵，这使得式(1)中的刚度项也是非对称矩阵。从数学上看，刚度矩阵不对称意味着特殊矩阵不对称，而不对称矩阵的特征值和特征向量在一定条件下为复数。从物理上看，刚度矩阵的不对称可能导致系统内部的能量馈入，从而成为不稳定系统。

设式(2)解的形式为:{x}={Φ}eλt，则有:

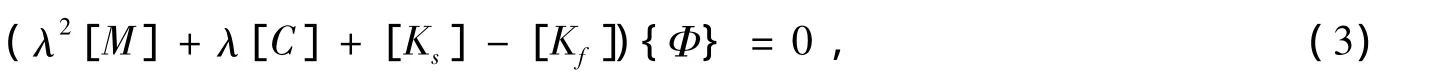
其中，{Φ}为特征向量;λ=α+iω为系统的特征值，实部α反映了系统运动的稳定性，虚部ω反映了振动时的固有频率。若α＞0则说明该阶模态振幅会随着时间的增加而增大，导致系统的发散，这样的模态被称为不稳定模态，可能导致制动噪声。

2 模型有限元分析

2.1 有限元模型的建立

在三维软件CATIA中建立制动盘、制动块以及制动钳支架的三维模型，进行适当的几何优化。在Ansys Worbench中建立3个部件的有限元模型，以及基于摩擦耦合的制动器有限元模型。根据厂家提供的数据以及GB5763—2008《汽车用制动器衬片》做线性材料替代处理，各部件的材料属性参数见表1。

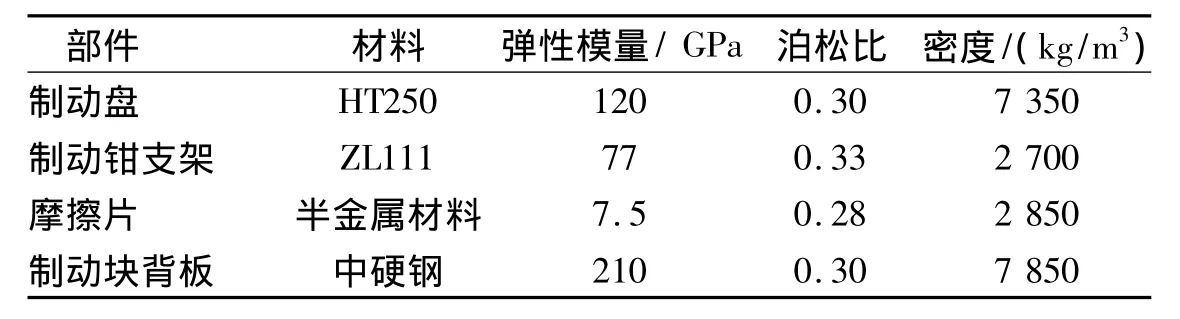
表1 各部件的材料属性参数

网格划分采用的是20节点的六面体单元Solid186以及10节点的四面体单元Solid187，合理选择自由网格或者映射网格，在摩擦面上进行网格的细化处理。在制动盘和摩擦片之间添加一个摩擦接触对，选择增广的拉格朗日接触算法，形成摩擦耦合模型。摩擦片和制动块背板是黏接在一起的，模型中添加绑定接触对。制动块和制动钳支架之间有止动弹簧，模型中两者用弹簧连接进行模拟。制动器有限元模型如图1所示。

2.2 部件实模态分析

对于一个典型无阻尼自由振动系统，其模态分析过程是经典的特征值求解问题[7］。

式中，[M］和[K］分别为系统的质量矩阵和刚度矩阵;{Φi}为第i阶模态的振型向量;ωi为第i阶模态的固有频率。Ansys具有强大的求解特征值的能力，对于规模较大、频域较宽的实模态分析，用分块Lanczos法求解比较合适[8］。

实模态分析之前要明确各个部件的约束条件。在制动器系统中，制动盘通过4个螺栓安装孔固定在轮毂上与前桥相连，因此，在计算实模态时4个安装孔表面节点要约束所有的自由度。制动块仅和制动盘、制动钳相连，和制动器之外的部件没有任何连接，实模态分析时直接计算其自由模态。制动钳支架依靠两个螺栓安装孔固定在转向节上，因此，在分析时要约束两个安装孔表面节点的所有自由度。在Workbench Modal模块中分别进行实模态分析，提取各部件0～15 kHz的模态。制动盘的第1阶和第9阶模态如图2所示，第1阶模态(1.037 kHz)是制动盘的径向弯曲模态，第9阶模态(3.403 kHz)是制动盘断面的弯曲模态，呈波浪形。

2.3 复模态分析

在进行复模态分析之前，先要进行非线性静力学分析，获取制动器在给定的油管压力、制动盘转速以及约束条件下的应力-应变状态，得到系统的非对称刚度矩阵 之后进行复模态分析，提取系统的各阶模态，获取系统的不稳定模态。具体步骤如下:

图2 制动盘第1阶和第9阶模态

(Ⅰ)在内侧制动块背板上施加制动压力，进行非线性静力分析，建立系统的接触应力状态。

(Ⅱ)给制动盘施加角速度，模拟制动盘与摩擦片之间的滑动状态，非线性分析获取系统在给定参数下的完整应力-应变状态，系统此时的刚度矩阵为非对称。

(Ⅲ)在Ansys中利用非对称法进行复模态的提取，获得系统的不稳定模态。

根据噪声出现时的工况，现取制动压力为3 MPa、制动盘角速度5 rad/s、摩擦因数为0.3，依据上述步骤进行计算，复模态提取范围为0～12 kHz。需要指出的是:用非对称法进行模态提取时，实部代表模态的频率，虚部为表征系统稳定性的量，模态是实部和虚部的综合结果。由计算得到系统的3组虚部大于零的复特征值，分别为:第23阶4 756.9+17.197i、第42阶7 909.1+28.246i、第48阶9 615.1+22.345i。这3组模态是制动器系统的不稳定模态。

3 试验与结果分析

噪声试验所用的紧凑型制动惯量试验台由电机舱、惯量模拟舱、试验舱3部分组成，主要用于轻型车、轿车等制动器的综合性能测试[10］，在密闭的试验舱里安装麦克风和声压仪。

据工况设定微型车的整车模拟惯量，参考SAE j2521《盘式制动噪声试验标准》在不同的初始速度、制动压力下进行盘式制动器的制动试验，图3为一次噪声出现时的频谱，声压大于70 dB的频段为650～950 Hz。试验发现在4～6 kHz声压大于70 dB的噪声发生概率为5.8%，在8～10 kHz声压大于70 dB的噪声发生概率为5.3%，都超过了标准要求的2%。复模态分析中发现的3组不稳定模态与上述试验结果是基本吻合的，判断制动噪声还要进行具体的分析。

大量的试验发现:制动噪声与制动盘的径向弯曲有直接的联系，制动噪声频率约等于径向弯曲时制动盘的固有频率[11-12］，根据这一规律可以推测可能的制动噪声频率。查看复模态分析中3组模态的振型，第42阶模态实部主要是内制动块及制动钳支架一侧的弯曲变形(模态分析中的变形都为相对变形)引起的振动，不符合制动噪声的产生规律。判定该制动器系统与制动噪声相关的不稳定模态为第23阶、第48阶，可能的制动噪声频率为4.757 kHz和9.615 kHz。

查看制动器系统第23阶模态实部和虚部的变形以及在6个自由度上的振型参与系数，制动盘盘面外沿部分径向内外弯曲，中间法兰面四周内外凸凹变形也比较大。内侧制动块一边沿弧线方向发生扭转，与之相连一侧的制动钳支架悬臂弯曲变形比较大，另一侧也有较小的弯曲变形。在实模态分析中，各部件与系统第23模态相关的模态为制动盘第17阶(4.673 kHz)、制动块第8阶(4.833 kHz)、制动钳支架第9阶(4.776 kHz)，如图4所示。

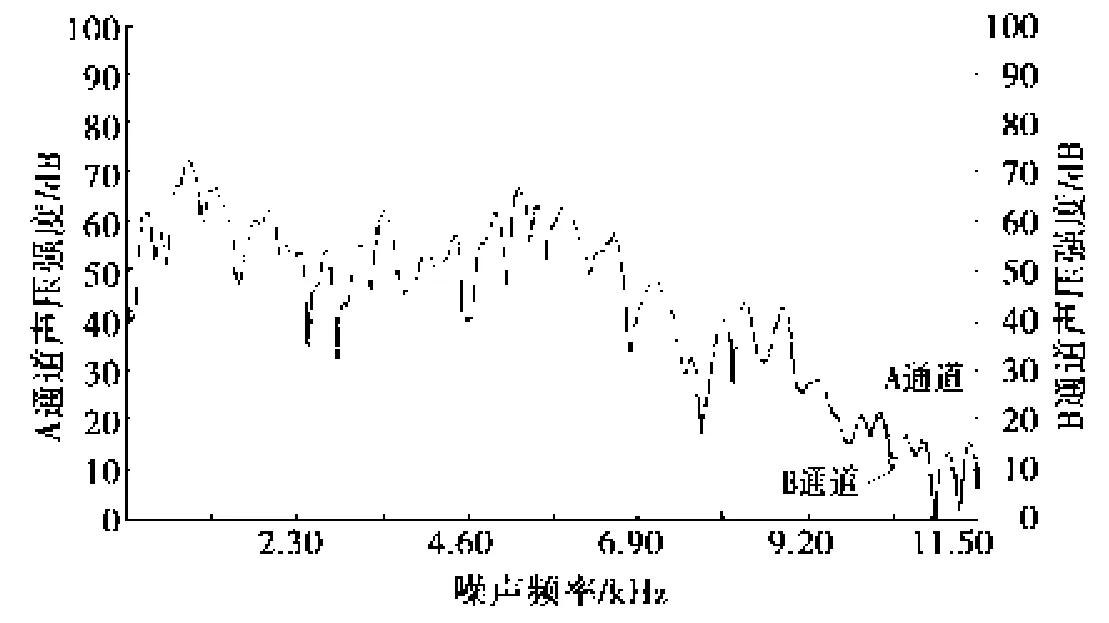
图3 一次噪声出现时的频谱

图4 与系统23阶模态相关的各部件模态

同理，查看制动器系统第48阶模态，制动盘盘面以及中间法兰面沿周向发生了较大变形，呈波浪形。制动块中间部分内外弯曲，一侧发生扭转。制动钳支架的两侧都出现弯曲，变形角度不大。在实模态分析中，各部件与系统第48阶模态相关的模态为制动盘第34阶(9.496 kHz)、制动块第10阶(10.073 kHz)、制动钳支架第14阶(9.445 kHz)。

图5 修正后系统第36阶模态

由结果分析可知:制动盘的第17阶和第34阶盘面部分都出现了弯曲变形，同时中间法兰面也都出现了凹凸变形，可以通过改变法兰面厚度以及盘面的结构使其固有频率避开噪声发生的频率;对于制动块，两个相关模态都出现了一侧扭转变形，可以改变材料参数以及加工工艺使其固有频率发生变化;对于制动钳支架，可以通过改变边梁和悬臂的结构来改变其固有频率，实现降噪目的。制动盘法兰面加厚1 mm，制动块与制动钳支架间止动弹簧的接触刚度、阻尼修正后进行复模态分析，结果只出现了一个不稳定模，即第36阶模态7 197+7.861i，由于其振动状态(见图5)并不符合制动噪声的产生规律，制动器系统没有出现与噪声相关的不稳定模态。

4 结论

根据某微型车制动噪声出现的实际工况，本文基于有限元实模态和复模态分析方法，结合制动噪声试验对其进行了分析。由结果可以看出文中提出的解决方案是可行的，对降低制动噪声有指导作用。主要有以下结论:

(1)基于摩擦耦合的制动器系统有限元模型能近似反映制动噪声发生时的实际工况，摩擦接触导致了系统刚度矩阵的不对称，使得系统出现制动噪声。

(2)复模态分析能得到系统的不稳定模态，结合噪声试验可以获取系统可能的制动噪声频率。查看不稳定模态振型，在实模态分析中可以得到噪声发生时各部件的振动状态。

(3)基于噪声发生时各部件的相关模态频率和振动状态，可以提出结构参数优化方案，通过隔振以及转移频率的措施来实现降噪目的。

[1]余为高，于学华.汽车制动噪声产生机理及控制方法[C］//中国环境科学学会学术年会论文集.北京:北京航空航天大学出版社，2009:1290-1294.

[2]李兵，王庆波.基于Ansys的盘式制动器制动噪声分析[J］.贵州大学学报:自然科学版，2012，29(3):112-115.

[3]管迪华，宿新东.利用子结构动态特性优化设计抑制制动器尖叫[J］.汽车工程，2003，25(2):167-170.

[4]刘伯威，杨阳，熊翔.汽车制动噪声的研究[J］.摩擦学报，2009(4):385-390.

[5]候俊，过学讯.基于有限元方法的盘式制动器噪声研究[J］.机械设计，2008，25(8):50-52.

[6]周冠嵩.汽车盘式制动器振动与噪声研究[D］.上海:同济大学，2008.

[7]靳晓雄，张立军，江浩.汽车振动分析[M］.上海:同济大学出版社，2002:108-110.

[8]马文哲.最新经典ANSYS及Workbench教程[M］.北京:电子工业出版社，2004:378-386.

[9]付薛洁，石博强，姜勇，等.基于ABAQUS的湿式多盘制动器制动噪声分析[J］.煤矿机械，2012，33(2):99-101.

[10]孙鹏龙，付主木，王周忠.并联式混合动力汽车再生制动控制策略[J］.河南科技大学学报:自然科学版，2013，34(3):35-39.

[11]John D F.A Proposal to Predict the Noise Frequency of a Disc Brake Based on the Friction Pair Interface Geometry[DB］.USA:SAE Technical Paper Series，1999-01-3403V001.

[12]Mario T J，Samir N Y，Roberto J.Analysis of Brake Squeal Noise Using the Finite Element Method:A Parametric Study[J］.Applied Acoustics，2008，69:147-162.