液压混合动力汽车燃油经济性最优控制策略

李训明，曲金玉，刘 林，魏 伟，田香玉

(1.山东理工大学交通与车辆工程学院，山东淄博255049;2.潍柴动力股份有限公司新能源中心，山东潍坊261000)

0 引言

液压混合动力车辆动(HHV)力系统由发动机与液压泵/马达双动力源组成，两动力源之间合理的能量分配策略是提高车辆燃油经济性的关键。为了提高液压混合动力汽车的燃油经济性，国内外学者进行了很多相关研究。文献[1-2］利用“if-then”形式控制规则，采用基于规则的控制策略，其功率输出是用一个非线性含参函数来表达的，这种控制策略依赖于车辆传动系统拓扑结构及行驶工况，通用性及可移植性较差。文献[3］利用动态规划算法对燃油经济性优化目标函数进行求解，将有限层优化问题转化为有限的计算问题，该算法是解决有约束非线性问题的有效方法，但要获得精度相对较高的解，需要增大动态网格密度，由此会造成计算量巨大，求解时间非常长。文献[4-8］利用模糊逻辑设计了模糊控制器，通过优化各部件的工作效率，在保证车辆性能的前提下，保证车辆经济性与排放性最优，但模糊控制规则依靠经验制定，当车辆参数及行驶工况发生变化时，控制规则必须重新建立，其通用性及可移植性较差。本文主要研究了液压混合动力汽车的燃油经济性最优控制问题。首先，介绍了液压混合动力汽车动力系统结构及整车评价目标;其次，依据庞特里亚金最小值原理，在液压混合动力系统状态方程的约束下，建立了整车燃油经济性Hamilton最优目标函数，通过求解Hamiton目标函数得出了液压混合动力汽车能量分配最优控制策略。最后在Matlab/Simulink仿真环境下搭建了整车仿真模型，并在欧州循环行驶工况(NEDC)下对最优控制策略进行了验证。研究结果表明:能量分配最优控制策略能够提高燃油经济性26%以上。

1 液压混合动力车辆动力学模型

1.1 液压混合动力系统结构

本文选用宇通ZK6126HG公交车作为试验车，满载时总质量16 500 kg，在城市工况中，此公交车发挥着重要作用。液压混合动力汽车动力系统结构如图1所示。

动力系统采用柴油机和液压马达作为动力源，两动力源采用并联方式连接。电磁离合器分离与结合将整车工作模式分为发动机与液压马达混合驱动、发动机单独驱动、液压马达单独驱动、制动回收能量等工作模式。在制动能量回收模式时，液压油从低压油箱流向高压蓄能器，在液压驱动模式时，液压油从高压蓄能器流向低压油箱 ，高压蓄能器采用气囊式液压蓄能器，其整车结构参数如表1所示。

1.2 最优控制目标函数

液压混合动力汽车最优控制的目标是车辆在特定的循环工况中运行时，在满足动力性要求的前提下所消耗的总燃油量最小，则目标函数可表示为:

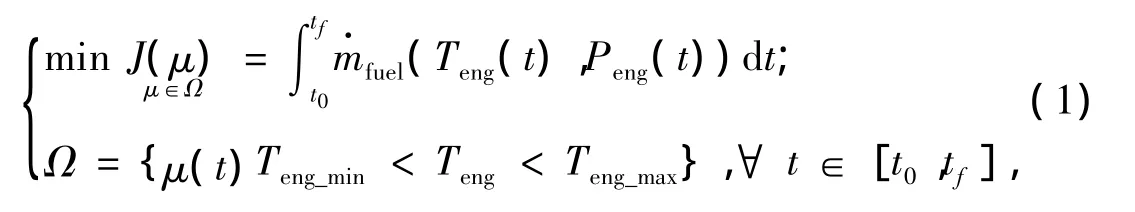
式中，J为优化目标函数;mfuel(t)为发动机油耗总质量;Peng(t)为发动机功率;Teng(t)为发动机输出扭矩;Ω为控制变量容许取值区域。

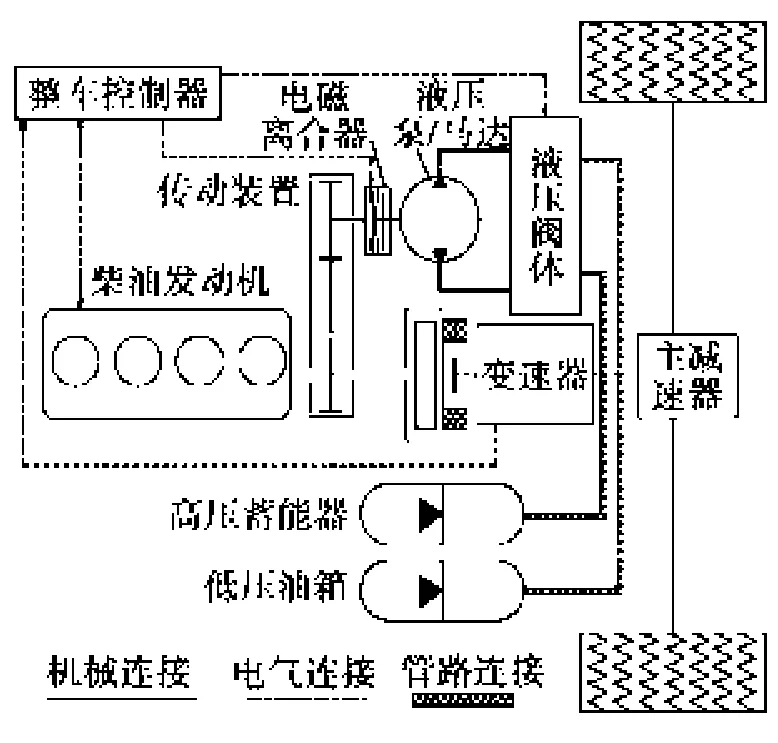
图1 液压混合动力系统结构原理图

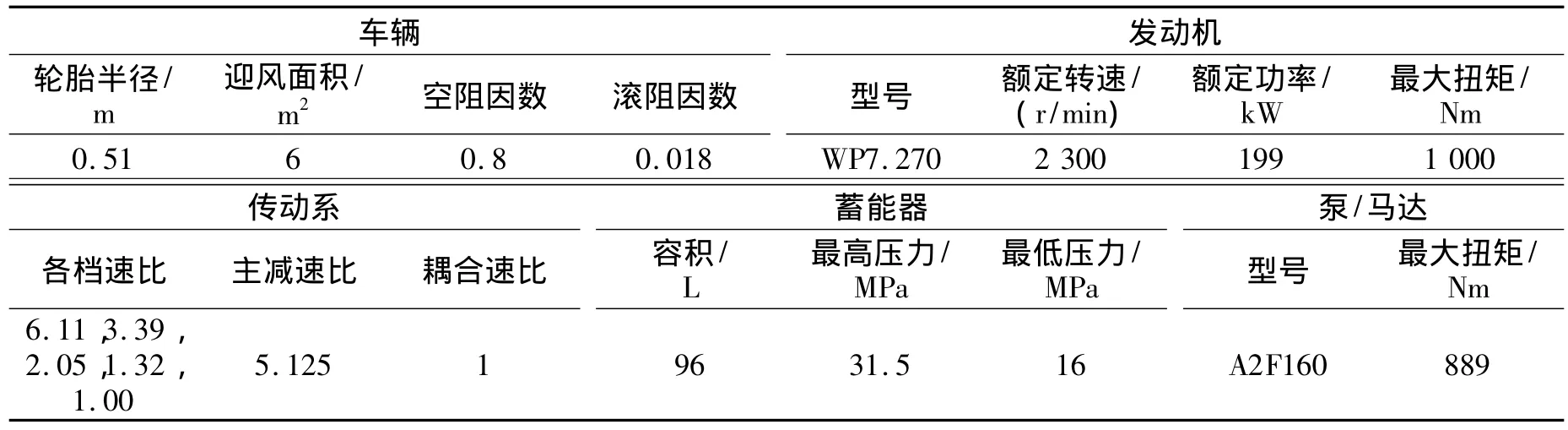
表1 液压混合动力系统结构参数

1.3 系统约束条件

液压混合动力系统是一个高度非线性的复杂系统，其约束条件可以分为两大类:一类称为机械约束，另一类称为性能约束。其中，机械约束包括发动机输出的转矩、转速允许范围和液压泵/马达允许的转速、转矩和流量范围;性能约束包括蓄能器工作压力允许范围、系统流量允许范围及车辆在特定循环工况下应满足的燃油经济性能指标。

式中，Te为发动机输出转矩;Mp为液压马达输出转矩;ωe为发动机输出转速;ωp为液压马达输出转速;p为液压蓄能器工作压力;Qp为液压蓄能器流量;Vliq为液压蓄能器工作容积。

1.4 系统状态方程

液压蓄能器具有功率密度大，能量密度小，全充全放能力强的特点[10］，因此，液压蓄能器存储与释放能量是在很短的时间内完成的，可以认为这个过程为绝热过程。当回收制动能量时，气体温度升高，当释放能量时，气体温度降低。本文选用液压蓄能器内气体温度作为状态变量，为了更加近似地表示液压蓄能器内气体的p-V-T特性，可采用Benedict-Webb-Rubin方程[11-12］来建立系统状态方程，气体压力变化方程为:

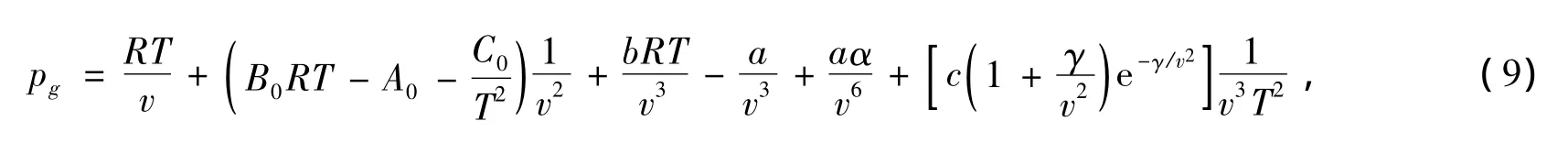
式中，pg为气体绝对压力;R为理想气体常数;T为气体热力学温度;v为气体比体积;A000α、γ为BWR方程常数。液压蓄能器气体满足的规律:

式中，p0为液压蓄能器充气压力;V0为液压蓄能器容积;p1为液压蓄能器的工作压力;V1为液压蓄能器在压力p1下的容积;n为多变指数，等温过程n=1，绝热过程n=1.4。

液压蓄能器气体能量平衡方程[13］:

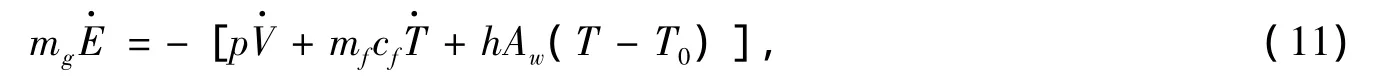
式中，mg为蓄能器气体质量;E为液压蓄能器内储存的能量;mf为隔热材料质量;cf为隔热材料比热容;h为单位质量传热系数;Aw为液压蓄能器壁的有效面积;T0为环境温度。

联立式(9)～式(11)得液压蓄能器气体温度变化状态方程:

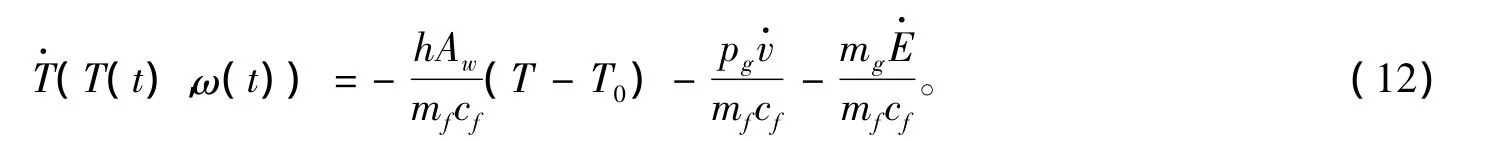
不妨定义初始状态液压蓄能器能量为零，此时液压蓄能器气体温度等于外界大气温度，末状态固定，即液压蓄能器气体温度应满足条件:

2 Hamilton函数的建立与求解

本文所研究的问题属于高度非线性、初末状态固定、有约束的最优控制问题，一般通过变分法、极小值原理或动态规划[14］等解决。本文依据庞特里亚金极小值原理，通过构造Hamilton函数来对目标泛函求解。

Hamilton函数为:

协态方程为:

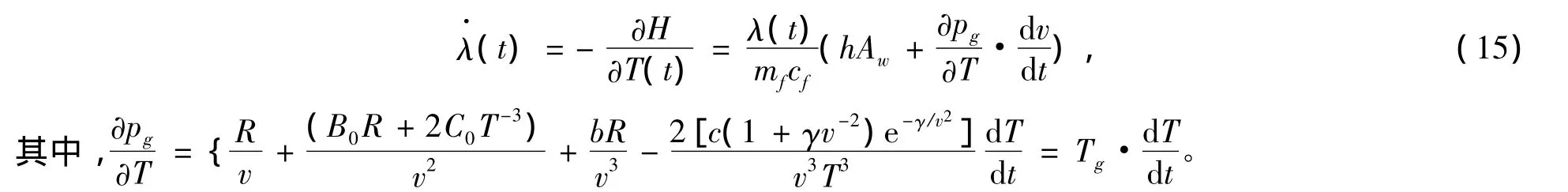
控制变量为:

Hamilton正则方程为:

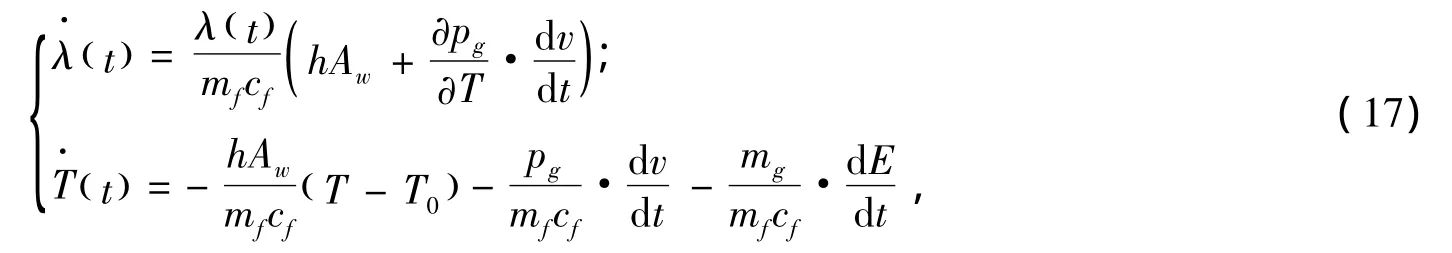
解Hamilton正则方程得:

边界条件为:

据庞特里亚金极小值原理，在最优轨线T*(t)和最优控制P*p(t)上目标泛函极小值存在的必要条件为:

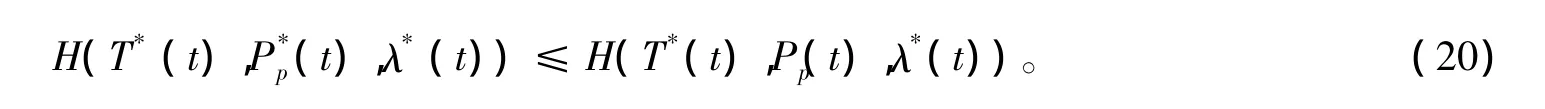
联立式(9)～式(14)和式(18)得最优控制变量Pp应满足的条件为:

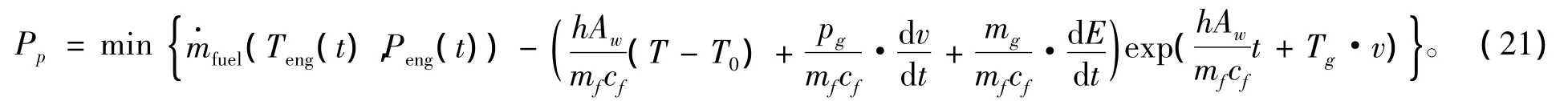
对于本文所研究的液压混合动力汽车经济性最优控制问题，根据最优控制必须满足的条件，确定出最优控制规律，得出最优控制策略。

3 仿真结果分析

在Matlab/Simulink平台中搭建了整车仿真模型，利用表1中的数据对最优控制策略进行仿真验证。图2～图4分别为仿真循环工况、驱动扭矩及换档规律曲线。

3.1 传统控制与最优控制的比较

图5～图7分别为液压混合动力汽车采用传统控制策略与最优控制策略发动机功率、油耗率与百公里油耗仿真结果对比图。由图5～图7可以看出:最优控制策略使发动机输出功率、燃油消耗率与百公里油耗都明显降低。

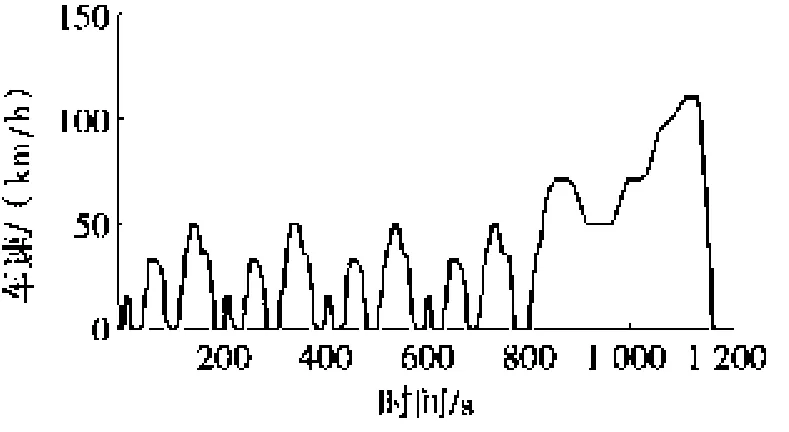
图2 NEDC循环工况曲线

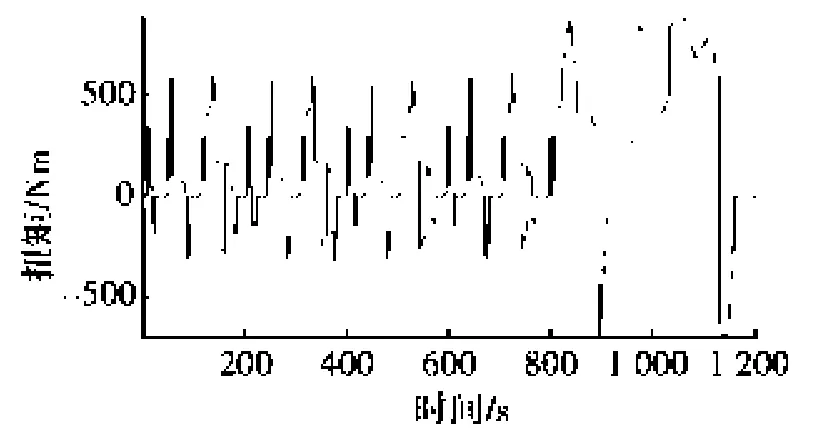
图3 HHV需求扭矩曲线

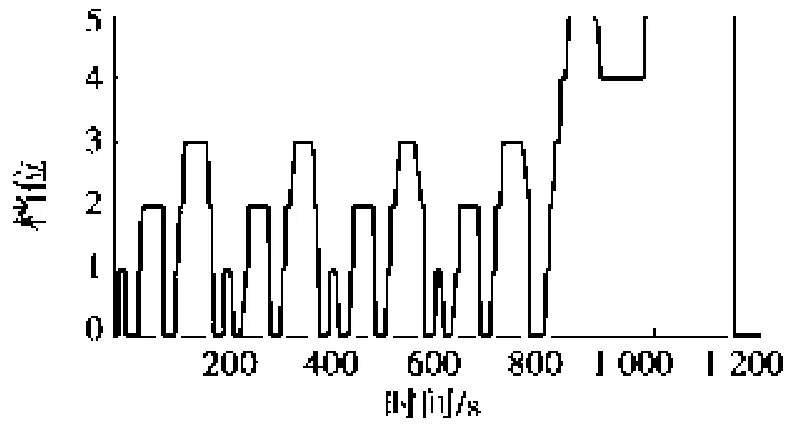
图4 换档规律曲线图

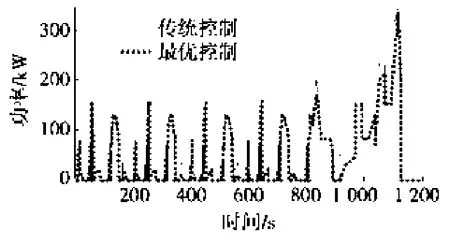
图5 发动机功率对比

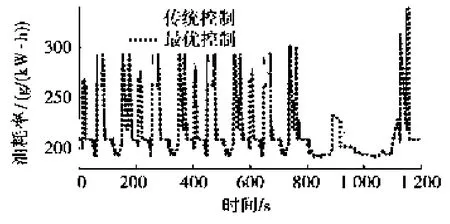
图6 油耗率对比图

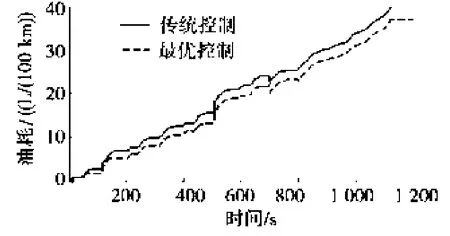
图7 百公里油耗对比图

3.2 发动机起停最优控制对燃油经济性的影响

为了分析发动机起停对整车燃油经济性的影响，在最优控制策略中加入发动机起停控制，最终得到发动机起停最优控制策略。

图8～图10分别为发动机起停优化控制策略对发动机功率、燃油消耗率及整车油耗的影响，可以看出整车燃油经济性进一步提高。

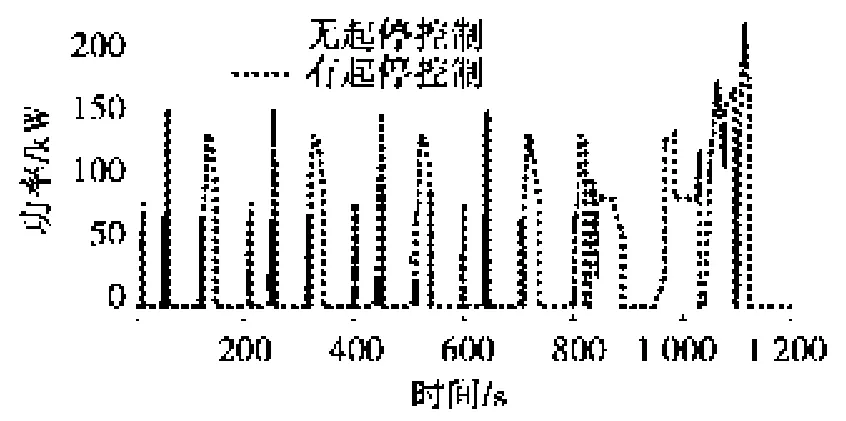
图8 起停控制对发动机功率影响图

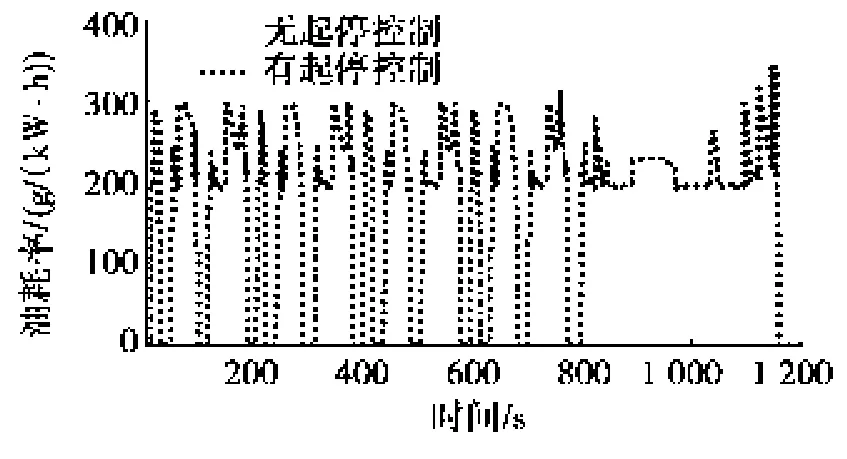
图9 起停控制对发动机油耗率影响图

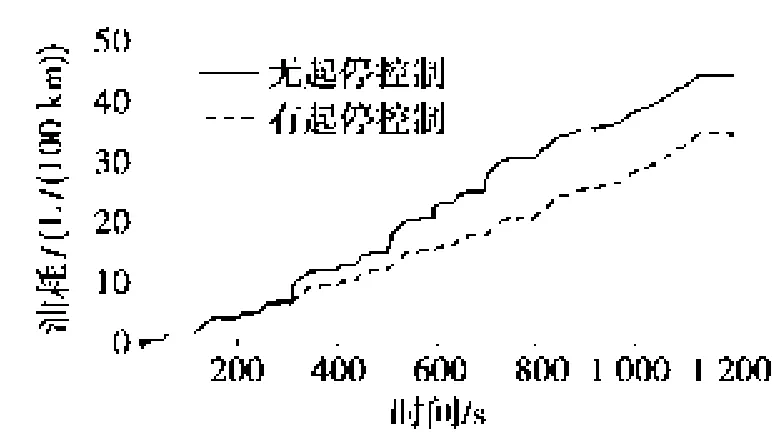
图10 起停控制对整车油耗影响图

表2为液压混合动力汽车在有发动机起停控制与无发动机起停控制情况下，分别采用传统控制策略与最优控制策略下的仿真油耗对比数据，由表2可见:加入发动机起停控制的最优控制策略燃油经济性改善明显。

表2 NEDC工况油耗对比

4 结论

本文研究了液压混合动力汽车燃油经济性最优控制问题，提出了一种能量分配最优控制策略，通过仿真验证得到如下结论:(1)相对于基于规则的传统控制，最优控制策略降低了发动机输出功率及燃油消耗率，使发动机工作在最优区间，从而整车燃油经济性提高12.82%。(2)在最优控制策略基础上加入发动机起停优化控制，发动机的输出功率及燃油消耗率进一步降低，整车燃油经济性提高26.19%。

[1]Lin C，Peng H，Grizzle J W，et al.Power Management Strategy for a Parallel Hybrid Electric Truck[J］.IEEE Trans:Control Systems Technology，2003，11(6):839-849.

[2]Wu B，Lin C，Filipi Z，et al.Optimization of Power Management Strategies for a Hydraulic Hybrid Medium Truck[C］//Advanced Vehicle Control Conference.Hiroshima，2002.

[3]Koot M，Kessels J T B A，de J B，et al.Energy Management Strategies for Vehicular Electric Power Systems[J］.IEEE Trans:Vehicular Technology，2005，54(3):771-782.

[4]Wang D Y，Lin X，Zhang Y.Fuzzy Logic Control for a Parallel Hybrid Hydraulic Excavator Using Genetic Algorithm[J］.Automation in Construction，2011，20(5):581-587.

[5]Schouten N J，Salman M A，Kheir N A.Energy Management Strategies for Parallel Hybrid Vehicles Using Fuzzy Logic[J］.Control Engineering Practice，2003，11(2):171-177.

[6]Kheir N A，Salman M A，Schouten N J.Emissions and Fuel Economy Trade-off for Hybrid Vehicles Using Fuzzy Logic[J］.Mathematics and Computers in Simulation，2004，66(2):155-172.

[7]Poursamad A，Montazeri M.Design of Genetic-fuzzy Control Strategy for Parallel Hybrid Electric Vehicles[J］.Control Engineering Practice，2008，16(7):861-873.

[8]高建平，李晓林，杨博.混合动力汽车工况聚类分析与模糊控制策略[J］.河南科技大学学报:自然科学版，2012，33(4):19-22，27.

[9]孙鹏龙，付主木，王周忠.并联式混合动力汽车再生制动控制策略[J］.河南科技大学学报:自然科学版，2013，34(3):35-39.

[10]刘涛，姜继海，孙辉，等.静液传动混合动力汽车的研究与进展[J］.汽车工程，2009，31(7):586-591.

[11]Hui S.Multi-objective Optimization for Hydraulic Hybrid Vehicle Based on Adaptive Simulated Annealing Genetic Algorithm[J］.Engineering Applications of Artificial Intelligence，2010，23(1):27-33.

[12]范基，吴劲.蓄能器的蓄能性能研究[J］.液压工业，1990，2(2):1-6.

[13]姜继海，刘涛.汽车液驱混合动力技术[M］.北京:机械工业出版社，2011.

[14]张洪钺，王青.最优控制理论与应用[M］.北京:高等教育出版社，2007.