高动态导航自适应噪声带宽跟踪技术仿真研究

徐 娟，毕彦博，王 伶，姚如贵

（2.长安大学 电控学院，陕西 西安 710064；2.西北工业大学 电子信息学院，陕西 西安 710129）

高动态导航自适应噪声带宽跟踪技术仿真研究

徐 娟1，毕彦博2，王 伶2，姚如贵2

（2.长安大学 电控学院，陕西 西安 710064；2.西北工业大学 电子信息学院，陕西 西安 710129）

为解决载体高动态运动引发的多普勒效应给卫星导航接收机捕获、跟踪、定位带来的问题，本文研究了一种动态调节环路噪声带宽的方法，即将卡尔曼滤波技术应用于跟踪环路。卡尔曼滤波是一种应用广泛的最优估值理论，基于它良好的预测性能，考虑将经典跟踪环路中的环路滤波器替换为卡尔曼滤波器。本文建立了相应的卡尔曼滤波模型，选择合适的环路跟踪参数作为系统状态量和观测量，并搭建高动态仿真环境，对其环路跟踪性能较之传统跟踪环路做了对比分析。结果表明，该方案具有更强的环路适应能力，在高动态、低信噪比环境下具有较好跟踪性能。

高动态；导航跟踪；动态噪声带宽；卡尔曼滤波

随着国防技术的飞速发展，导弹等军事武器的高动态应用环境愈加复杂，因而近些年来高动态卫星导航接收机技术一直是国内外相关领域研究热点[1,7]。在高动态环境下，载体高速、高加速度运动引起的多普勒效应给接收机信号的捕获、跟踪和定位带来了挑战。高动态通常指载体运动具有比较高的速度、加速度、加加速度。JPL(美国喷气动力实验室)在高动态GPS信号跟踪技术方面作了较深入的研究，并取得了较多的成果。V.A.vilnroter, S.Hinedi和S.Agurr等研究了扩展卡尔曼滤波(EKF)、叉积自动频率控制环(CPAFC)，频率扩展卡尔曼滤波(FEKF)、数字锁相环(DPLL)等算法在高动态环境中的多普勒频率估计性能。

文献[2]研究将EKF用于高动态环境下的载波相位估计，同时估计载波相位和多普勒漂移，得到比较好的估计误差和动态性能指标；文献[3]在算法推导层面比较分析了高动态环境下EKF、MLE（最大似然估计）、ALS（自适应最小均方算法）等几种跟踪方案；文献[4]仿真分析了EKF算法的估计精度和动态跟踪能力。以上对卡尔曼滤算法或EKF算法在跟踪中的应用研究有如下特点：方法中应用的状态模型都是非线性模型，处理过程较复杂；载波跟踪环路和码跟踪环路分别用一个单独的卡尔曼滤波器来代替原有的环路滤波器；模型中系统过程噪声和测量噪声的统计特性在处理过程中被设定为固定值，导致算法自适应能力比较弱。

文中采用基于卡尔曼滤波理论的自适应跟踪策略，采用四阶线性状态模型和更加紧凑的环路结构，在保证跟踪性能和环路自适应能力的基础上使处理过程更为简单。

1 传统跟踪环路噪声带宽分析

传统导航接收机数字载波跟踪环路中，环路滤波器是影响载波环路性能优劣的主要部分。采用数字锁相环跟踪的导航接收机，其数字环路滤波器是由模拟锁相环中的最佳环路滤波器进行双线性变换离散化得到的，离散间隔为信号预检测积分时间。数字环路滤波器设计过程中的主要参数有环路阶数、阻尼系数和环路等效噪声带宽Bn（以下简称噪声带宽）。

噪声带宽控制经过环路滤波器的噪声数量。为了降低环路噪声，噪声带宽应保持为一个较小的值。但同时，由于导航信号中存在有一定的动态应力，接收机本地的晶振也存在相位噪声，较小的噪声带宽不能保证环路的稳定跟踪。因此，要保证接收机的环路跟踪性能，就必须对噪声带宽进行合理设置。一般根据接收机工作环境下需要接收的强度最弱的信号和所要求支持的最高的用户动态应力来选择一个恰当的噪声带宽。研究分析得，噪声带宽大，载波环能很快锁定频率，但同时锁定状态下的频率噪声相对较大；噪声带宽小，则载波环需要一些时间才能锁定频率，但锁定后频率稳定性较好（前提是动态扰动不超过噪声带宽范围）。在一次跟踪过程中，适当调整噪声带宽，可以实现环路收敛速度和收敛精度的双重改善。因而研究系统适用的自适应噪声带宽跟踪技术非常必要。

2 卡尔曼滤波模型构建

卡尔曼滤波可以解决的问题是对一个离散时间线性系统的状态进行最优估算，因而它具有良好的预测性。图1所示为一种将卡尔曼滤波器用于GPS信号跟踪环路的设计方案，该方案与传统跟踪环路的不同在于，本地复现码生成和复现载波NCO的频率更新来自于卡尔曼滤波器的处理结果。

图1 基于卡尔曼滤波器的跟踪环路原理图Fig. 1 Kalman filter based tracking loop

2.1 系统状态方程

式(1)是所建立的四阶线性状态方程[5]，其具体表达方式见式(2)。其中所选的前三个状态变量是用于载波跟踪的，分别是相位差、多普勒频率和多普勒频率变化率；最后一个状态变量用于码环跟踪。

式(1)中，Xk、Xk-2代表k、k-1时刻系统的状态向量，A为状态转移矩阵，B为在系统输入量与系统状态之间的关系矩阵，w代表过程噪声向量。系统输入量U是可选项，有些系统可以没有输入量。式(2)中，Xp是接收信号真实载波和本地复现载波的相位差，其单位是rad；xω是载波的多普勒频移，单位是rad/s；xa是载波的多普勒频移变化率，单位是rad/s2；xτ是接收信号真实码相位与本地复现码相位的差值，其单位是码片数；ΔTk是两次计算的时间间隔，也是一次预检测积分时间；k表示第几次测量；ωNck是本地载波复现时在中频基础上的自然角频率偏移；fck是本地复现C/A码时码速率在1.023 MHz基础上的偏移；wk-1是4×1的过程噪声向量，主要包括卫星和接收机相对运动的影响，以及由电离层波动引起的码和载波之间不同步而带来的噪声。方程参数中的1540是GPS L1载波与C/A 码频率之比。

2.2 系统测量方程

式(5)是所建立的系统测量方程，其具体表达形式见式(6)。

式(5)中，C为观测量与系统状态间的关系矩阵，D为观测量与输入量之间的关系矩阵，vk表示噪声向量。选用的观测量为Δφk和ΔTk。Δφk是第k次预检测积分时间ΔTk内，信号真实载波和本地复现载波的平均相位差；Δτk是第k次预检测积分时间ΔTk内，信号真实码相位与本地复现码的平均相位差，单位是基码码片数。vk是2×1测量噪声向量。实际观测量来自环路鉴别器的输出，本文中的载波环和码环鉴别器选用的鉴相算法分别为二象限反正切算法和归一化超前减滞后包络算法。

式中，IEs、IPs、ILs、QEs、QPs、Qs分别是I、Q支路第k次预检测积分的超前、即时、滞后相干累加值。

2.3 滤波稳定性判别与环路更新

卡尔曼滤波稳定性定理[6]是：如果随机线性系统是一致完全可控和一致完全可观测的，则卡尔曼滤波器是一致渐近稳定的。

对于式(2)和式(6)描述的系统，一致完全随机可控、一致完全随机可观测的判别式可写为式(8)和式(9)的形式[6]，其中n是系统维数，rank是矩阵的秩。在实际中ΔTk为0.001s的情况下，很容易计算得到此两式成立，所以由卡尔曼滤波稳定性判定定理，可推知本次卡尔曼滤波过程一致渐近稳定，即当滤波时间足够长后，卡尔曼最优滤波值将渐近地不依赖于滤波初值的选取。

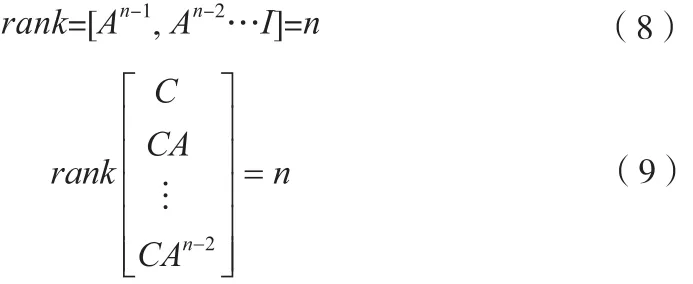
在第k次运算后，卡尔曼滤波器的输出Xk是状态向量的最优估计值，则ΔTk时段yk的最优估计Δφk和Δτk就可由Xk带入式(6)得到；进而ΔTk-1时段本地载波和本地C/A码NCO频率的更新递推计算可由下式(10)和(11)完成。其中ka和kb是可调系数，用于调节本地载波和本地 码NCO的更新速率，本文中ka和kb分别取0.6、0.9。

3 高动态运动目标设计

文中所研究的信号基于高动态环境，但是用于高动态分析的真实数据不容易获得，因而常见的研究方法为设计建立模拟高动态运动目标跟踪模型。本节以GPS系统为例设计高动态运动目标模型，并进行Matlab环境下的GPS信号生成。

高动态指标设计主要表现在对运动目标加加速度的设定上，本文仿真用到的加加速度设定如图2(a)所示，其值最高达到10 gm/s3，图2(b)和图2(c)所示为在此加加速度变化基础上计算得到的加速度和速度显示。由动态引起的附加在载波上的多普勒频移由式(12)计算可得，

式中fc为载波频率，此处选用 波段频率1575.42 MHz，C为光速。图2(d)所示多普勒频移变化情况。

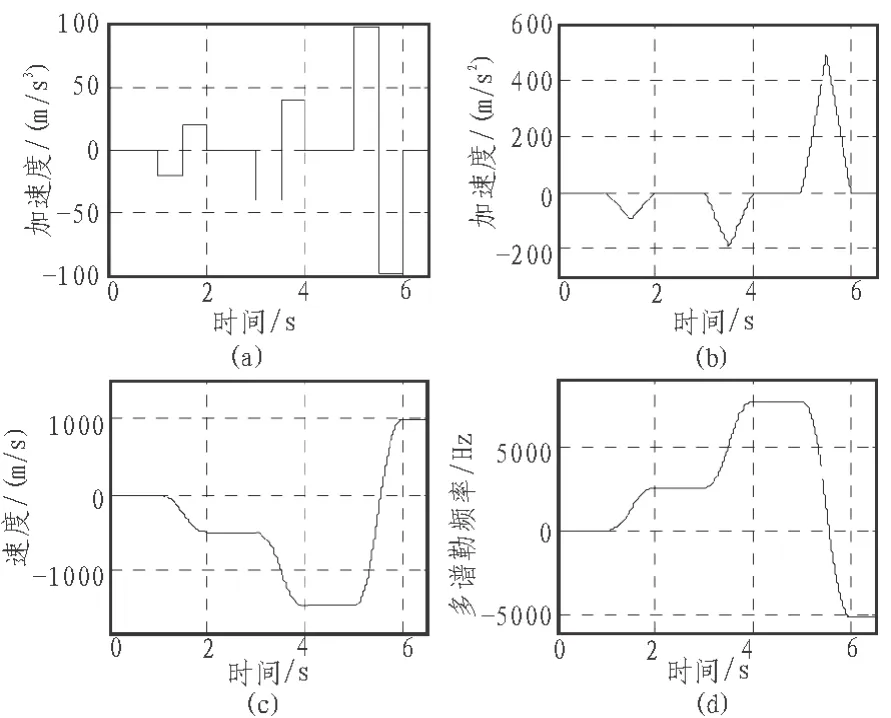
图2 高动态指标设定Fig. 2 Settings of high dynamic index

1)中频信号的合成

GPS信号是由载波信号调制了 码和导航电文后生成的。混频后的载波数字中频设定为9.548 MHz，它是连续的正弦波，不过由于动态的影响频率上会附加有多普勒频移； 码为速率1.023 M基码/秒的伪随机码，周期为1 ms；导航电文是50 Hz的数据。三种信号使用双相相移键控(BPSK)调制。

由动态引起的多普勒频移是中频信号合成过程中最重要的一个参数，它根据运动模型的设计计算得到。仿真中，按照图4给出的高动态模型加加速度、加速度、速度的变化趋势及式(12)首先计算得到原始的多普勒频移数据。对该数据进行1ms为周期的采样、量化，以体现其变化趋势。最后将采样后的数据转化为频率控制字，叠加到中心频率的控制字上。

2)噪声产生

信号中的噪声可用典型的零均值高斯白噪声来模拟。设噪声功率谱密度为N0，噪声带宽为Bn，则噪声功率Pn=N0×Bn。信号载噪比C/N0与信噪比SNR之间的关系为：

式中，Ps为信号载波功率。

普通接收机可以处理的信号载噪比在35-55 dBHz的范围内，下文的仿真中设为40 dBHz ，GPS中频信号噪声带宽约为2 MHz，带入式(13)计算得SNR为-23 dB 。

3)仿真信号的采样、量化

对已经叠加了噪声的中频信号进行采样，采样频率设为38.192 MHz。采样后对合成的数字信号进行4 bit 量化。

4 仿真分析与对比

在Matlab环境下，本节分别应用传统环路跟踪方法和基于卡尔曼滤波的跟踪算法对同一段仿真数据进行了处理和对比。

图3～图5所示为传统载波跟踪环路跟踪结果，其环路参数设置为：预检测积分时间1 ms；二阶PLL噪声带宽25 Hz；DLL噪声带宽2 Hz；环路阻尼因子0.7。由图3可见，0N1 s无动态情况下，PLL环约在94 ms左右实现了收敛，此后的PLL鉴相器输出接近0，直到1s后第一个大小为2 gm/s3的加加速度出现，环路在极短的时间内就变为了发散状态，且不能再次收敛。图4为捕获模块输出结果，可见捕获输出的粗略多普勒值36 Hz在图5所示的PLL跟踪结果中得到了反映，环路发散前PLL的跟踪结果在36 Hz上下浮动，且浮动范围不超过±4 Hz，这也验证了PLL环能够达到无动态下的跟踪精度。但高动态下，PLL环路的输出情况并不理想。

按照上文给出的系统状态方程和系统测量方程搭建卡尔曼滤波跟踪模型，滤波初值和环路更新上文已给出，图6和图7所示为基于卡尔曼滤波理论的环路跟踪结果。图6所示为应用该算法跟踪到的载波多普勒频移，对比动态模型，表明此时环路可以很好地跟踪高动态变化，并且能够保持稳定，环路没有失锁。图7为卡尔曼滤波算法调节更新下PLL鉴相器的输出，其纵轴幅度的单位为rad，相位误差在加加速度达到10 gm/s3时出现最大值-0.2365 rad，即13.55°，均方差为0.0483 rad，即2.77°，按照3σ准则[8]，PLL环相位误差均方差经验门限为15度，故本结果在误差容许范围内。

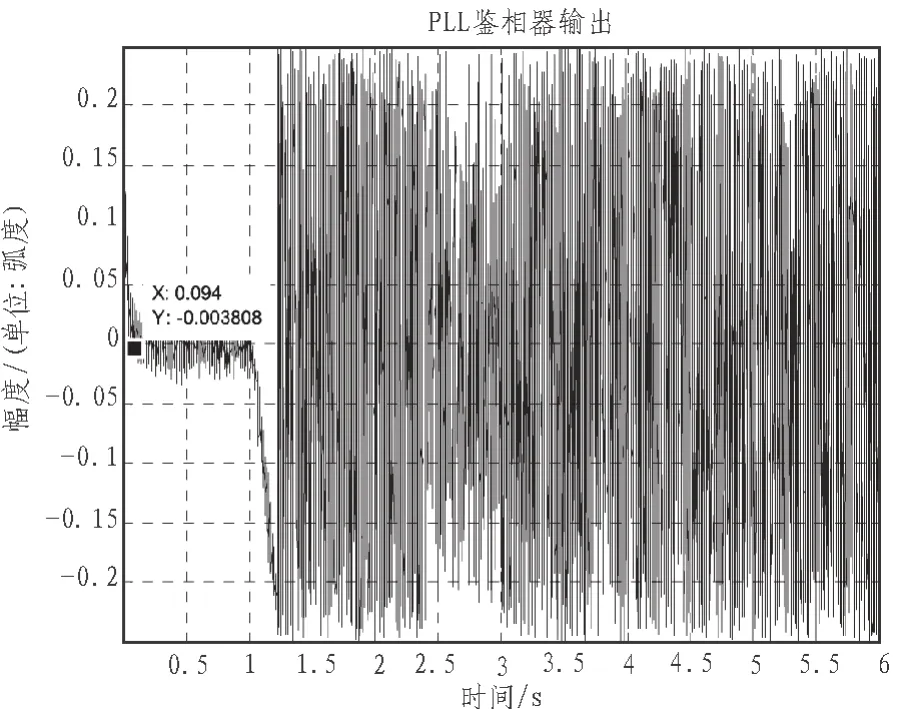
图3 传统跟踪环路PLL鉴相器输出Fig. 3 PLL discriminator outputs in traditional tracking loop

图4 传统跟踪环路PLL环路跟踪结果Fig. 4 PLL loop outputs in traditional tracking

图5 传统跟踪环路PLL环路跟踪结果Fig. 5 PLL loop outputs in traditional tracking

5 结 论

文中研究了高动态环境下导航系统跟踪策略，选择载波相位差异、多普勒频移、多普勒频移变化率和码相位差异为状态量建立四阶线性卡尔曼状态模型。比较验证结果得出，基于卡尔曼滤波理论的自适应噪声带宽跟踪算法在高动态环境下有更强的适应能力和更好的跟踪性能。此外，由于系统模型中矩阵阶次较低，可以将该算法移植到以高速 为处理核心的导航接收机平台上。因此，基于卡尔曼滤波的高动态导航自适应噪声带宽跟踪技术对于星载、弹载等特殊场景，具有较好的工程应用前景。

图6 卡尔曼滤波跟踪算法PLL跟踪结果Fig. 6 PLL loop outputs inKalman filter tracking

图7 卡尔曼滤波跟踪算法PLL鉴相输出Fig. 7 PLL discriminator outputs inKalman filter trackingloop

[1]王慧君.精确制导武器中应用的GPS接收机新进展[J].电光系统,2007(4):47-52.

WANG Hui-jun.New developments of GPS receivers used in precision guided weapons[J].Electronic and Electro-optical Systems,2007(4):47-52.

[2]李小民,田庆民.适应高动态环境的GPS载波相位估计方法研究[J],武汉大学学报:工学版,2003,36(3):20-124.

LI Xiao-min,TIAN Qing-min. Study of GPS carrier phase estimation method in high dynamic circumstances[J].Engineering Journal of Wuhan University,2003,36(3):20-124.

[3]王伟,张廷新,史平彦.高动态环境下GPS信号跟踪算法综述[J].空间电子技术,2000(1):1-9.

WANG Wei,ZHANG Ting-xin, SHI Ping-yan.GPS signal tracking algorithm under high dynamic environment[J].Space Electronic Technology,2000(1):1-9.

[4]吕艳梅,李小民,孙江生.高动态环境的GPS信号接收及其算法研究[J].电光与控制,2006,13(4):24-27.

LV Yan-mei, LI Xiao-min, SUN Jiang-sheng.GPS signal receiving and its algorithmsunder high dynamic circumstances[J].Electronics Optics & Control,2006,13(4):24-27.

[5]左启耀,袁洪,林宝军,等.基于Kalman滤波理论的高动态GPS信号跟踪系统仿真研究[J].系统仿真学报,2009,21(8):2160-2164.

ZUO Qi-yao,YUAN Hong,LIN Bao-jun,et al.Simulation research of high dynamic GPS signal tracking system based on Kalmanfiltering theory[J]. Journal of System Simulation,2009,21(8):2160-2164.

[6]秦永元,张洪钺,汪淑华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社,2004.

[7]Petovello M,O Driscoll C,Lachapelle G.Carrier phase tracking of weak signals using different receiver architectures[C]//ION NTM 2008 Conference, San Diego, CA,January 28-30,2008.

[8]Elliott D.K, Christopher J.GPS原理与应用[M].北京：电子工业出版社,2008.

Simulation research of adaptive noise bandwidth in high dynamic tracking

XU Juan1, BI Yan-bo2, WANG Ling2,YAO Ru-gui2
（1.School of Electronic and Control Engineering,Chang’an Unirersity,Xi’an70064,China;2.Northwestern Polytechnical University,Xi’an710129,China）

Under the high dynamic environment, theDoppler effects caused by the high speed and high accelerated motion have brought agreat challenge to the satellite signal acquisition, tracking and positioning. Mainly aiming at the high dynamic environment, this paper researches a kind of tracking loop optimization with adaptive noise bandwidth. A method of dynamic adjustment on loop noise bandwidth is researched in this paper, which is the technology of Kalman filter. Based on its better prediction performance, it can be applied in the tracking loop to replace a traditional loop filter.

High dynamic; Tracking; Adaptive noise bandwidth; Kalman filter

TN911.4

A

1674-6236(2014)07-0098-04

2014-01-17稿件编号201401132

国家自然科学基金项目(61301093,61271416); 航天支撑基金(2012-ht-XGD); 西北工业大学基础研究基金(JCY20130132)

作者简介：徐 娟(1980—)，女，陕西杨凌人，博士，讲师。研究方向：先进信息编码、高速数据传输技术等。