基于测试代价敏感的多粒度模糊粗糙集模型

徐苏平，杨习贝，范霁月，钱林峰，马 健

（江苏科技大学 计算机科学与工程学院，江苏 镇江 212003）

基于测试代价敏感的多粒度模糊粗糙集模型

徐苏平，杨习贝，范霁月，钱林峰，马 健

（江苏科技大学 计算机科学与工程学院，江苏 镇江 212003）

多粒度模糊粗糙集是经典多粒度粗糙集模型在模糊环境下的有益扩展，然而，已有的多粒度模糊粗糙集并未考虑考虑数据的测试代价，为解决这一问题，本文提出了基于测试代价敏感的多粒度模糊粗糙集模型，分析了其相关性质。研究表明，本文提出的模型是传统多粒度模型在应用背景下的有力扩展。

测试代价敏感；多粒度； 模糊；粗糙集

作为一种处理不精确、不确定性问题的数学工具，粗糙集理论[1](Rough Set)自上世纪80年代由波兰学者Pawlak 提出后便受到了广泛关注。目前，粗糙集理论已被广泛应用于模式识别、知识发现、决策支持、机器学习等众多研究领域[2-5]。

但是，众所周知的是，Pawlak的粗糙集模型本身较为简单，是建立在仅仅一个不可分辨关系的基础上的，而钱宇华等人认为在决策分析问题中，多个决策者之间的关系有可能是相互独立的，因而需采用多个二元关系来进行目标的近似逼近，为此他提出了多粒度粗糙集的概念[6-9]。在钱宇华的多粒度粗糙集中，他采用了两个及两个以上的不可分辨关系进行概念的近似逼近，并分析了多粒度粗糙集与经典粗糙集之间的关系。在钱宇华的多粒度粗糙集中，主要有两种不同的近似逼近方式，一种是多粒度乐观粗糙集方法，另一种是多粒度悲观粗糙集方法。多粒度粗糙集与经典粗糙集最大的不同就是它可以使用多个粒空间中的知识来进行概念的近似逼近。在多粒度的框架下，国内外众多学者做了大量的研究工作，完善充实了多粒度模糊粗糙集，值得一提的是，Yang等人和Xu等人将多粒度粗糙集引入模糊环境中，分别提出了多粒度模糊粗糙集模型[10-11]。

然而，值得注意的是，代价敏感学习[12]在数据挖掘等领域具有举足轻重的地位，所以研究基于代价敏感的粗糙集方法对于粗糙集理论的进一步发展是有着广泛的实际意义。就粗糙集本身的研究现状来看，代价分为误分类代价和测试代价。一方面, 决策理论粗糙集方法充分考虑了数据中的误分类代价和延迟决策代价。另一方面，在现实社会的工程应用中，数据的获取是需要付出一些成本或代价的，称其为测试代价。针对该问题, Min等人率先将测试代价引入到粗糙集的约简问题中. Yang 等人将测试代价引入到信息系统环境下粗糙集本身的近似模型上，提出了基于测试代价敏感的多粒度粗糙集。

文中将模糊多粒度粗糙集与测试代价紧密结合，提出了基于测试代价敏感的模糊多粒度粗糙集模型，研究该粗糙集模型的相关性质，并将其与传统的多粒度模糊粗糙集模糊进行对比分析。研究表明本文提出的基于测试代价敏感的模糊多粒度粗糙集模型是清晰环境下的基于代价敏感多粒度粗糙集的有效拓展，同时，在一定程度上依然保有传统模糊多粒度粗糙集的相关性质。

1 预备知识

1.1 Pawlak 粗糙集与模糊粗糙集

形式化地，一个信息系统可被定义为二元组S= ＜U,AT＞,其中U表示所有对象的集合，称为论域；AT表示所有属性的集合。

对于∀a∈AT, 定义映射a:U→Va,Va表示属性a的值域，即a(x)∈Va(∀x∈U)。

在信息系统S中，根据属性集合AT, 可得到一个不可分辨关系形如

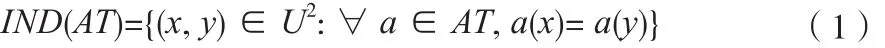
其中[x]AT={y∈U: (x,y)∈IND(AT)}表示U中所有与x具有不可分辨关系IND(AT)的对象的集合，即x的等价类。

Pawlak 经典粗糙集模型只能用于处理具有符号型、离散型的数据系统，为了进一步拓展粗糙集的应用范围，Dubios将其进入模糊环境，提出了模糊粗糙集模型。

令U为论域，定义在U上的一个二元模糊关系是一个映射形如

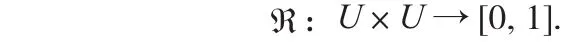
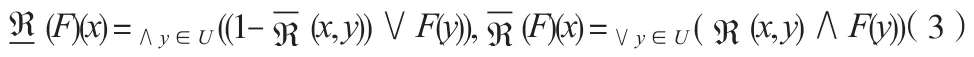
1.2 多粒度模糊粗糙集模型

由定义1可以发现，在经典粗糙集模型中，目标有且仅用一个二元关系近似逼近，为了满足现实生活中分布式数据的处理，Qian 等人提出了多粒度粗糙集，该粗糙集由一族二元关系来近似逼近目标。Qian 等人的粗糙集模型由两种不同的形式构成，分别是乐观多粒度粗糙集模型和悲观多粒度粗糙集模型。Yang等人立足于模糊环境，将多粒度思想引入模糊环境下提出了乐观多粒度模糊粗糙集和悲观多粒度模糊粗糙集模型。

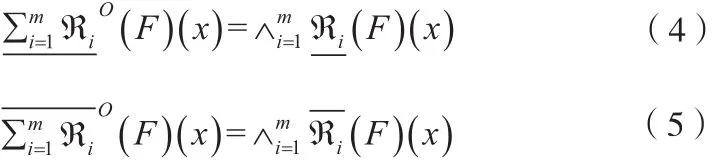
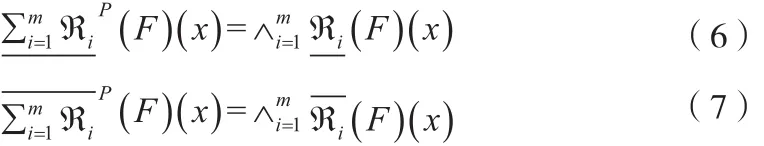
2 测试代价与模糊多粒度粗糙集

上节所涉及到的粗糙集模型都未考虑数据的代价问题,然而在现实工程应用中, 数据的获取并不是免费的. 为了解决这个问题, Min等人[]将测试代价引入到信息系统中,具体的描述见定义5.

2.1 基于测试代价敏感的模糊多粒度粗糙集的定义

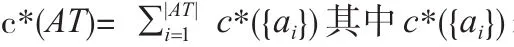
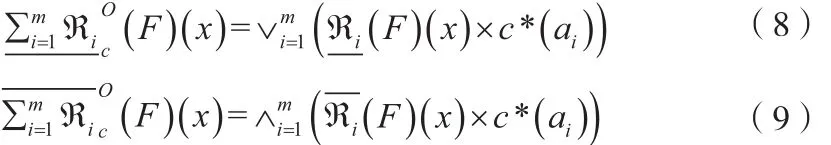
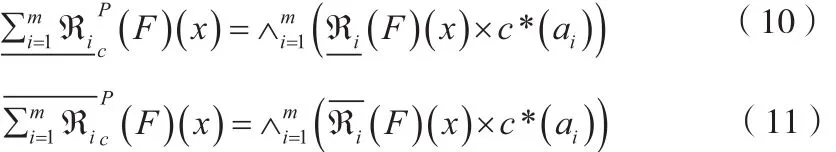
2.2 基于测试代价敏感的多粒度模糊粗糙集的性质

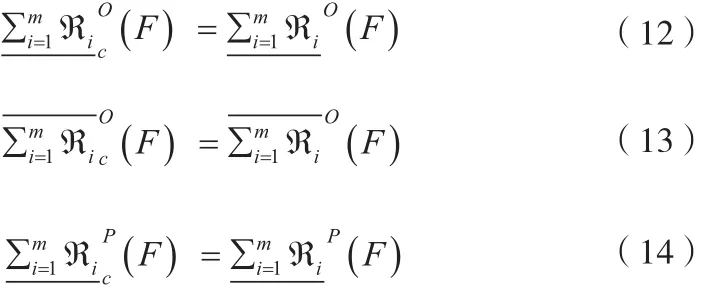
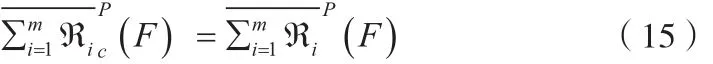
证：仅证公式(12)，其它公式类似可证。

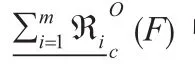
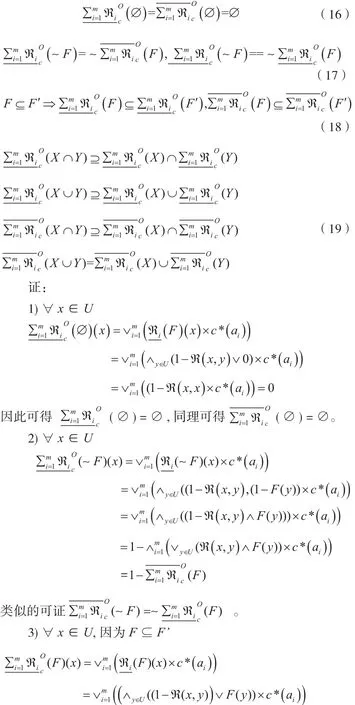
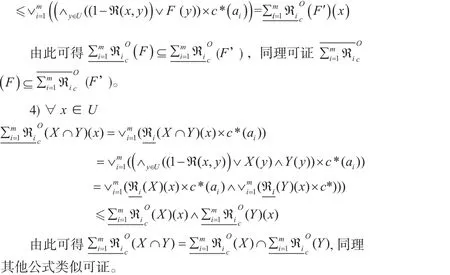
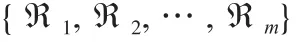
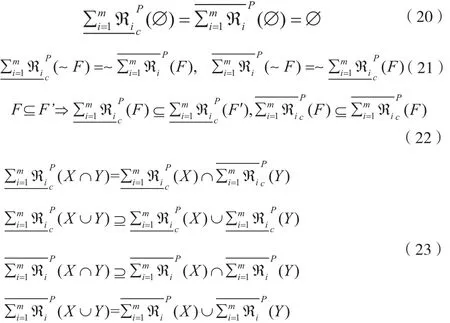
证：与定理2证明类似，故不再赘述。

3 结 论

文中笔者将多粒度模糊环境与测试代价相结合，提出了基于测试代价敏感的多粒度模糊粗糙集模型，即基于测试代价敏感的乐观多粒度模糊粗糙集和悲观多粒度模糊粗糙集。当所有属性的测试代价均为1时，基于测试代价敏感的乐观多粒度模糊粗糙集与悲观多粒度粗糙集分别退化为经典的多粒度模糊粗糙集。

[1]Pawlak Z.Rough sets-theoretical aspects of reasoning about data[M].Dordrecht: Kluwer Academic,1991.

[2]Luo G Z,Yang X B.Limited dominance-based rough set model and knowledge reductions in incomplete decision system [J].Journal of Information Science and Engineering,2010,26(6):2199-2211.

[3]Hu Q H,Che X J, Zhang L,et al. Rank entropy based decision trees for monotonic classification [J].IEEE Transactions on Knowledge and Data Engineering,2012,24(11): 2052-2064.

[4]Hu Q H,Pan W W, Zhang L, et al.Feature selection for monotonic classification [J].IEEE Transactions on Fuzzy Systems,2012,20(1):69-81.

[5]Xie G,Zhang J L, Lai K K,et al. Variable precision rough set for group decision-making: An application [J].International Journal of Approximate Reasoning,2008, 49(2):331-343.

[6]Qian Y H,Liang J Y.Rough set method based on multi-granulations[C]//in:5th IEEE International Conference on Cognitive Informatics,2006:297-304.

[7]Qian Y H,Liang J Y.Dang C Y,Incomplete multigranulation rough set [J].IEEE Transactions on Systems, Man and Cybernetics, Part A,2010,20:420-431.

[8]Qian Y H,Liang J Y,Wei W. Pessimistic rough decision [C].in:Second International Workshop on Rough Sets Theory,19-21,October 2010,Zhoushan,P.R.China: 440-449.

[9]Qian Y H,Liang J Y,Yao Y Y,et al.MGRS:A multi-granulation rough set [J].Information Sciences.2010.180:949-970.

[10]Yang X B, Song X N, Dou H L et al. Multi-granulation rough set:from crisp to fuzzy case [J].Annals Fuzzy Mathematics.Information, 2011,1(1):55-70.

[11]Xu W H,Wang Q R, Zhang X T. Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space [J].International Journal of Fuzzy Systems,2011,14:246-259.

[12]Min F,He H P,Qian Y H, et al.Test-cost-sensitive attribute reduction[J].Information Sciences,2011,181(22):4928-4942.

Test-cost-sensitive based multigranulation fuzzy rough set model

XU Su-ping, YANG Xi-bei, FAN Ji-yue, QIAN Lin-feng, MA Jian
（School of Computer Science and Engineering, Jiangsu University of Science and Technology,Zhenjiang212003, China）

Multigranulation fuzzy rough set is an expansion of the classical multigranulation rough set. However, the exist multigranulation fuzzy rough set model do not take the test cost of the data into consideration. To solve such problem, we propose a test-cost-sensitive based multigranulation fuzzy rough set model in this paper. And we also show the properties of this model. The result shows that, the model which is proposed in this paper is a powerful expansion with the classical multigranulation fuzzy rough set in real world application.

test-cost-sensitive; multigranulation; fuzzy; rough set

TN06

A

1674-6236(2014)07-0005-03

2013-08-04稿件编号201308037

国家自然科学基金(61100116, 61203024);江苏省自然科学基金(BK2011492，BK2012700);江苏省高校自然科学基金(11KJB520004);江苏省青蓝工程，高维信息智能感知与系统教育部重点实验室（南京理工大学）基金(30920130122005);中国科学院计算技术研究所智能信息处理重点实验室开放课题资助(IIP 2012-3)

徐苏平(1991—)，男，江苏扬州人。研究方向：粗糙集。