基于逐次二点法提高加工中心定位精度

何伟铭 贾江森 毛彦朋 封左伟 水洪伟

(上海理工大学机械工程学院，上海200093)

在机械加工领域，数控机床以自动化程度高、柔性好、加工精度高等优点在现代制造业加工中得到广泛应用。数控机床的精度是衡量数控机床设计与使用过程中性能优劣的重要指标，提高机床的精度有两种基本方法:误差预防法和误差补偿法。误差预防法是一种“硬技术”，通过设计和制造途径消除或减少可能的误差源，靠提高机床制作精度来满足加工精度要求。误差预防法有很大的局限性，即使能够实现，在经济上的代价往往是很高的。误差补偿法是使用软件技术，人为产生出一种新的误差去抵消当前成为问题的原始误差，通过统计、分析、归纳及掌握原始误差的特点和规律，使人为误差与原始误差尽可能数值相等、方向相反以提高精度。通过误差补偿可在机床上加工出超过机床本身加工精度的工件，是一种“精度进化”的概念。因此误差补偿是一种既有效又经济的提高机床定位精度的手段。符合我国现有的数控机床提高精度的要求，并且具有广阔的市场［1］。

逐次二点法(sequential two points method，STP)是由Tanka、Tozawa和Sato在1979年提出来的［2-3］，用于进行直线度误差的测量。并且逐次二点法具有误差分离简单，数据处理工作量小，速度快，对初始条件没有严格的要求等优点，只是忽略了测量支架的转角误差，如果被测长度相对于两传感器间距比较大时，在误差测量中是一种较好的方法。本文应用逐次二点法测量出机床的误差，根据测量得到的数据，对数控加工程序进行修改成为新的加工程序之后输入机床，实现误差补偿以提高加工精度。

1 逐次二点法简介

1.1 测量原理

如图1所示，逐次二点法采用安装距离为L的2个传感器，每次向前移动与安装距离相等的长度L，得到2个传感器在L的整数倍位置处的读数，通过数据处理可以同时得到所用机床的直线运动误差以及被测对象的直线度形状误差，推导公式如下。

假设初始条件Xi=0、Yi=0，则可以根据式(1)、(2)求出机床运动轨迹和工件表面误差。由于得出的是离散点的误差，可以根据需要利用插补的方法近似求出连续的误差值。

1.2 测量方法误差分析

逐次二点法本身存在着调零误差、转角误差以及环境变化等方面的影响。如图2所示，调零误差就是要求2个传感器测头安装时处在同一水平面，但实际上总会有一定的高度差Δ，Δ即调零误差。含有调零误差的公式如下。

若要求得调零误差Δ，可以利用逐次二点法先测量一条直线，得出初始点和终止点的高度差，然后用千分表测量直线的起始点和终止点，得出两点的实际高度差。将两个高度差相减再除以调零误差的累积个数，即可求出调零误差进行补偿。通过观察式(3)和(4)可知，调零误差在逐次二点法中是线性累积的，在图像上的体现是围绕着原点旋转了一个角度，利用最小二乘法对直线度、平面度评价时不产生影响［4］。

如图3所示，转角误差就是传感器固定在机床上时，夹具和机床运动所引起的传感器围绕着一点发生旋转偏移所产生的误差，该误差随着位置的不同而不同，产生的误差公式如下。

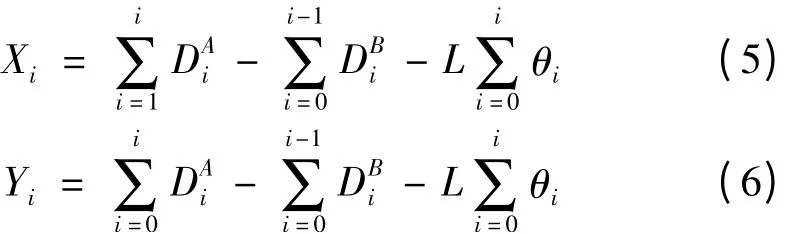
由此可知，被测对象误差和机床运动误差是转角误差的倍数累积，是逐次二点法的主要误差来源，无法从中分离出来。为消除该误差影响又开发出了逐次三点法等方法，但是，在本次实验中仪器精度较高，采样步长为20 mm，产生的转角误差较小，可以忽略不计。

2 逐次二点法在误差补偿上的应用

较早测量机床精度的方法是“圆形-菱形-方形”试切实验，但是这种方法受到标准件本身精度的影响，很难满足高精度机床的测量要求。9线法、14线法或22线法也可用来测量机床的各项误差，但是其前提是建立在准确测量线段长度的基础上。目前广泛采用的高精度测量方法是激光干涉法，可测量线性位置精度、重复定位精度、直线度、垂直度等，而且分辨率高、精度高。但其不足是测量时间长，技术要求高，对环境要求高，不适宜在生产现场操作［5］。

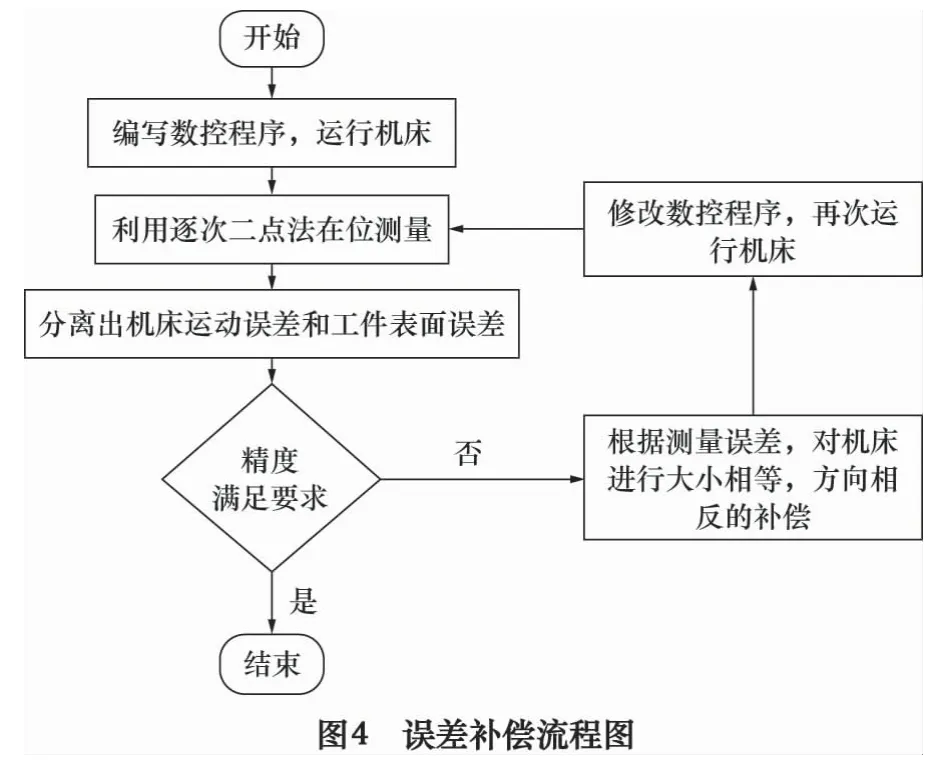
本文利用立式加工中心进行实验，应用逐次二点法在线测量出数控机床运动误差和被测对象的表面误差，根据得出误差结果对加工程序进行与误差大小相等、方向相反的补偿修改，利用修改好的程序再次进行测量实验［6］。如此反复进行补偿提高机床精度，直到再无法提高机床精度为止，这样可以得到高于机床本身精度的运动轨迹。其流程图如图4所示。本次实验测量已经加工好的合金铝板，采样步长为20 mm，以数控程序为基础进行数据的逐次采集，先补偿一条直线度误差，然后补偿10条X方向直线形状误差和1条Y方向边界直线形状误差，由一维直线向二维平面扩展，最后得到Z轴平面形状误差及补偿后误差形状。

3 误差补偿实验

3.1 实验系统

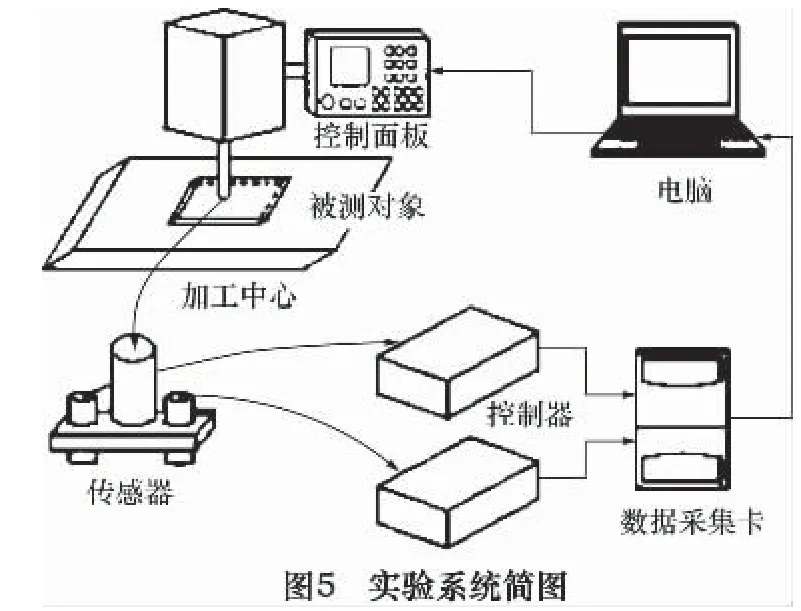
实验中所用机床是沈阳机床集团第一机床厂生产的VMC1165B立式加工中心，测量行程是X=1 100 mm、Y=650 mm、Z=610 mm，进给精度为1μm。传感器是日本ONOSOKKI公司生产的VE-521/VT-510型电容式位移传感器，测量精度为0.1μm。NR-110数据采集卡由日本基恩士公司生产，分辨率为14位、响应速度为20μs，可以将采集的数据自动储存在Excel文件中。实验系统还有设计好的传感器夹具、平行压板、电脑等组成。其连接简图如图5所示，实验平台连接图如图6所示。

3.2 实验结果与分析

VMC1165B立式加工中心基于FANUC系统编程，一些基本指令如下，绝对坐标尺寸指令G90、快速点定位指令G00、直线插补指令G01、程序结束指令M30、进给指令F等等［7］。依靠这些指令实现数控铣床运行，进行传感器数据的采集和误差的补偿。

传感器采集数据时，每个点采集5次，然后取其平均值作为测量的原始数据，以减小随机误差。通过数据采集卡传感器数据可以实时显示在Excel表格中，其中一条X方向直线的测量原始数据及补偿值如表1所示，其中传感器A、B是原始测量值，导轨误差是去除调零误差后的结果。

把这条直线进行反复误差补偿，可以得到加工中心在该位置上Z轴不同点的定位误差值，如图7所示。由图可知，已经无法再提高机床的定位精度。根据测量数据处理结果，按照最大最小值评价的方法，可知原始误差值为21.8μm，补偿后的最小误差值是15.8 μm，将其定位误差提高了27.52%。

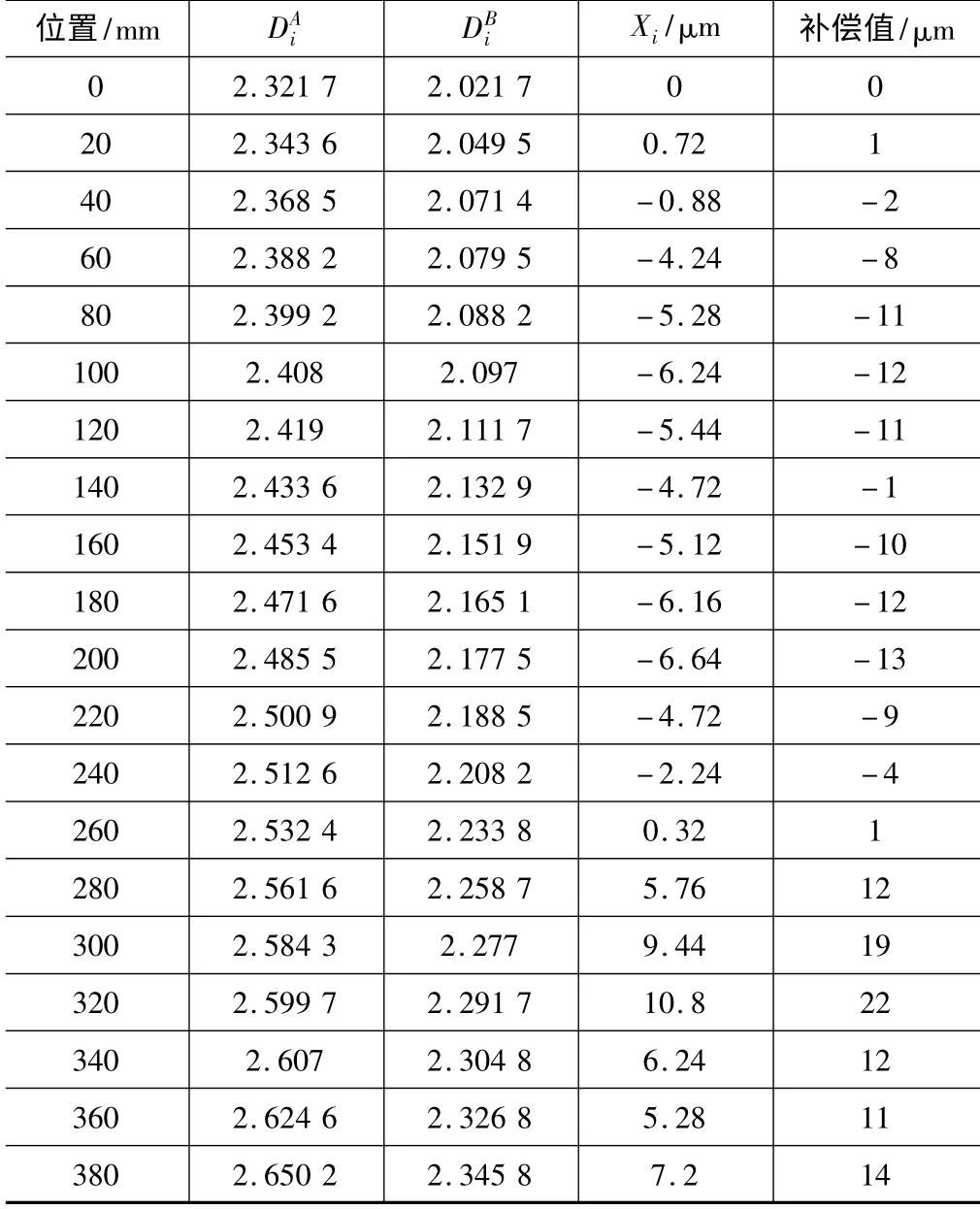
表1 测量数据及结果

利用同样的方法测量并且补偿Z=-55.800 mm处10条X方向直线和1条Y方向的边界直线，得到Z轴在该平面上的定位误差及其补偿效果。然后利用Matlab编程将图像显示出来［8］，进行直观的显示和比较。在Z=-55.800 mm处的Z轴运行轨迹如图8所示，进行误差补偿后位置误差如图9所示。

4 结语

在现代加工制造业中，机床的精度体现着一个国家机械制造业的制造能力和发展水平。而通过误差补偿的方法可以提高机床的定位精度，加工出精度更高的工件，方便高效、节省成本，提高经济效益，具有实用价值。本文通过实验证明:利用逐次二点法进行误差补偿提高机床的定位精度是可行的;并且逐次二点法测量原理简单，数据处理速度快，可以同时分离出机床和被测对象的误差;传感器的调零误差对机床误差评价没有影响;该方法可以推广应用到车床、磨床的加工制造以及三坐标测量机的检测等。

［1］沈金华.数控机床误差补偿关键技术及其应用［D］.上海:上海交通大学，2008.

［2］Tozawa K，Sato H，O—hori M.A new method for the measurement of the straightness of machine tools and machined work［J］.Trans.ASME Mech.Design，1982，104(3):587-592.

［3］Tanaka H，Sato H.Extensive analysis and development of straightness measurement by sequential two-points method［J］.Trans.ASME J.Engng Industry，1986，108(3):176-182.

［4］徐永凯，王信义.两点法测量直线度中传感器对齐误差的探讨［J］.宇航计测技术，1999，19(6):21-24.

［5］刘焕牢，李曦.数控机床几何误差和误差补偿关键技术［J］.机械工程师，2003，15(1):16-18.

［6］李圣怡，戴一帆.精密和超精密加工在位检测与误差分离技术［M］.长沙:国防科技大学出版社，2007:292-293.

［7］李虹霖.机床数控技术［M］.上海:上海科学技术出版社，2012:187-193.

［8］张贤明.MATLAB语言及应用案例［M］.南京:东南大学出版社，2012:82-93.