中国股市波动性解析：基于RS-GARCH模型族的实证研究

郭航

（黄淮学院，河南 驻马店 463000）

中国股市波动性解析：基于RS-GARCH模型族的实证研究

郭航

（黄淮学院，河南 驻马店 463000）

波动性是衡量股市风险和稳定的重要指标之一，对股市的健康发展具有重要影响。以上证指数为研究标的，利用RS-GARCH模型族对股市的波动性进行了比较研究。结果表明：相对于一般的GARCH模型族，RS-GARCH模型族明显改善了“伪持续”现象，能够更好地刻画股市的波动特征；A股市场存在明显的杠杆效应；在高波动状态下，利空和利好消息，对于A股市场波动率的影响时间更长。

股票市场；RS-GARCH模型族；波动性

一、引言

股价波动是证券市场中最普遍的现象之一，对投资者、企业和监管者均会产生较大影响。因此，波动性问题一直是众多学者关注的热点之一。

2008年次贷危机导致全球股市暴跌，为抑制经济下滑，各国央行纷纷放宽货币政策，伴随经济复苏，发达国家股市都呈现出修复性上涨。但中国股市却与中国经济作为全球经济复苏的一面旗帜背道而驰，在2012年创出了近四年的新低，上证指数年线全球罕见地收出三连阴，成为全球表现最差的股市之一。在这一背景下研究中国股市波动，衡量证券市场结构、参与主体、市场制度的变革对股市波动性的影响显得尤为重要。

二、文献综述

收益率方差是衡量收益率波动的重要指标，在对其研究中，通常假定扰动项服从正态分布、t分布等既定分布，既波动的方差是稳定的。随着对收益率方差的研究发现，扰动的稳定性通常要比假设差，而且在不同时期预测能力呈现不同精准程度。为解决扰动方差的变动问题，恩格尔（Engle R，1982）[1]开创性的提出ARCH模型用以刻画方差的特征后，此后，条件异方差模型被广泛运用于时间序列研究中，特别是在金融研究领域。Bollerslev(1986)[2]在Engle的基础上进一步建立了广义自回归条件异方差模型(GARCH)，对波动性的预测效果有明显提升。在ARCH和GARCH模型的基础上，很多学者为了刻画波动率的不同特征进行了大量的研究，诸如EGARCH和TGARCH等模型，形成了GARCH模型族。大量研究显示股市波动确实受结构变化的影响，不同状态、不同国家均有不同的特征，因此后续的更多研究将带有机制转换的Markov链融入了GRACH模型，构建了RS-GARCH模型，相对于不考虑结构变化的模型，RS-GARCH模型的预测精度明显提高。

我国对波动变化结构模型研究开始比较晚，且主要集中于汇率、利率、股市收益率等方面。谢赤、刘潭秋(2003)[3]利用Markov模型研究了人民币对美元的汇率问题，赵留彦、王一鸣和蔡婧(2005)[4]则研究了通胀问题。王建军(2007)[5]利用蒙特卡洛方法模拟马尔科夫时间序列，对马尔科夫机制转换的理论方法进行了创新性研究。赵鹏、曾剑云(2008)[6]以上证综指为样本，构建了马尔科夫机制转换模型。万军等（2008）[7]用沪市高频数据为研究样本，利用RS-GARCH模型研究了股市波动问题。李丽[8]（2011）基于ARMA-GARCH模型剖析了股价与成交量之间的关系。

本文将从四个角度对A股市场进行研究：一是比较GARCH模型族与RS-GARCH模型族对刻画我国A股市场特征的准确性；二是研究利空消息和利好消息对A股市场收益率的影响；三是区分高波动状态和低波动状态下对消息的持续时间的影响；四是市场结构、制度变迁对波动率的影响。

三、RS-GARCH模型族介绍

RS-GARCH模型族是在GARCH模型的基础上，融合了马尔科夫转换过程，突破了GARCH模型的残差在不同状态下同方差的假设，同时假设模型的截距也符合马尔科夫转换过程。

实践研究发现，收益率具有偏态分布的特征，负向冲击和正向冲击的力度是不对称的，前者更容易增加股市的波动性，模型构建中引入虚拟变量以反映杠杆效应，可得到RS-TGARCH模型。同样，为了扩大条件方差的信息源，捕捉条件方差和扰动项之间的关系，也可以对条件方差模型进行拓展，得到RS-EGARCH模型，RS-EGARCH模型不仅不用通过假设就满足条件方差非负数的约束，而且可以更形象地捕捉到收益率的非对称特性，为模拟数据提供更多参考模型，有利于选择和预测。

四、实证研究

本文以2000年1月4日—2011年12月30日上证每日收盘价的290个数据为研究样本，采用RSGARCH模型族和传统的GARCH模型族进行分析。分别从拟合、预测和是否降低“伪持续”现象等几个角度进行研究分析。

（一）描述性统计分析，对数收益率直方分布图①由于数据绝对值很小，因此处理数据时将日收益率数值扩大1000倍作为模型的数据，以Rt命名此时间序列。

如图1、2所示，极端数值时有发生，表明收益率具有厚尾特征。另外波动呈现比较明显的聚集特征。

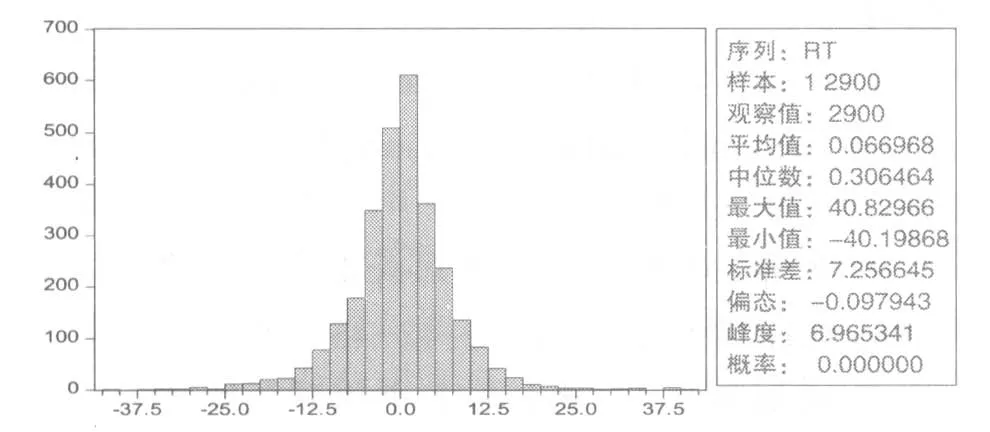
图1 上证指数日收益率直方图

图2 上证指数日收益率直线图

从统计值来看，从p值为零，收益率具有明显的ARCH效应。

表1 上证指数日收益率ARCH LM检验

（二）模型分析

利用收益率数据，可从模拟结果、预测误差和持续性三个角度综合比较GARCH模型族和RSGARCH模型族在刻画股市波动时的精度。

1.模拟结果比较

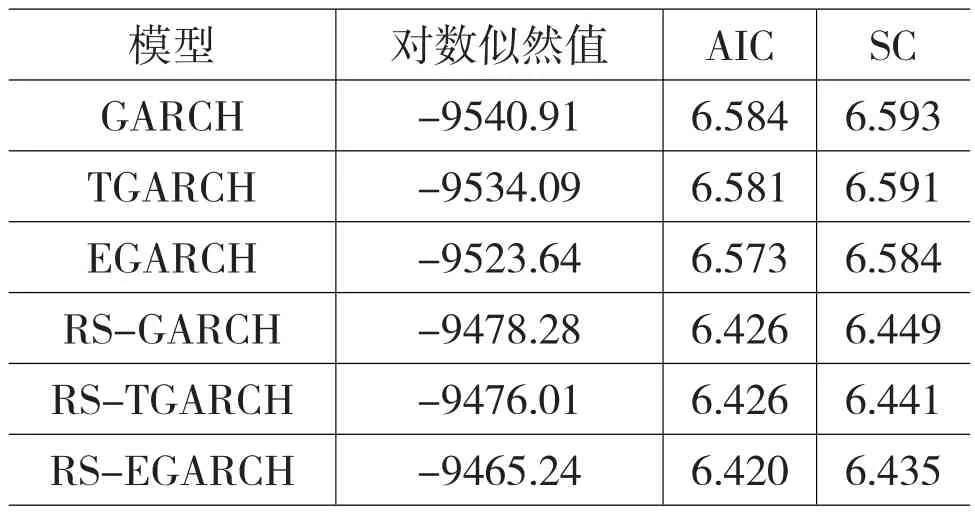
表2 模型估计结果比较

由表2比较对数极大似然值、AIC信息准则和SC信息准则三个指标可以看出：一般的GARCH模型族，这三个统计指标均大于RS-GARCH模型族，这说明RS-GARCH族更优于GARCH模型族；未考虑对称性的GARCH模型和RS-GARCH模型，其AIC、SC值均高于相应的对称模型，这说明考虑收益率的非对称性能够提升模型的拟合精度；在非对称模型中，EGARCH模型优于TGARCH模型，RSEGARCH模型优于RS-TGARCH模型；

2.预测误差比较

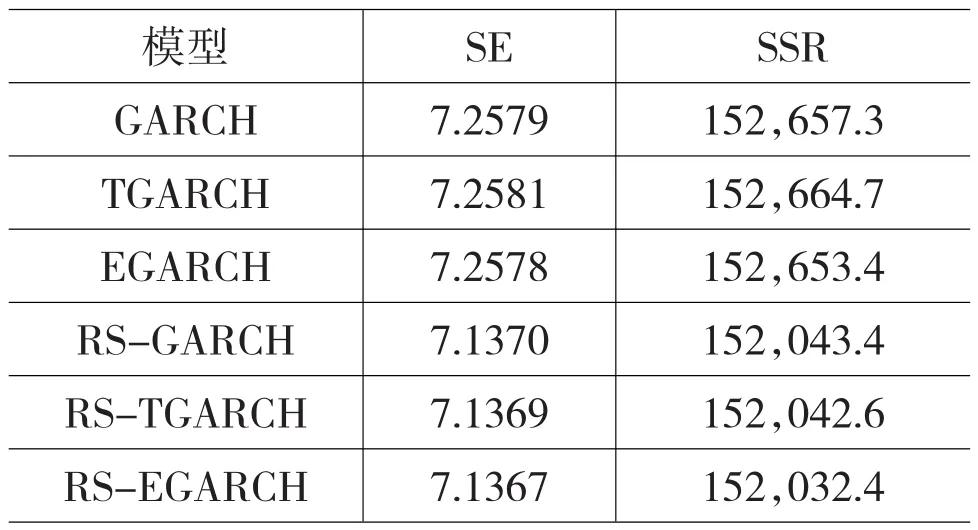
表3 模型预测能力比较

预测误差是衡量模型预期能力的一个重要指标，方程的预测能力与方程的残差平方和密切联系，当模型的预测方差较大时，区间估计的也随之宽广，预测的可信度就将降低。

RS-GARCH模型族预测误差明显低于GARCH模型族的预测误差；在GARCH模型族中，EGARCH模型的预测误差最小；在RS-GARCH模型族中，RSEGARCH模型的预测误差最小。

3.持续性比较

伪持续现象是GARCH模型族的一个重要缺陷，引进区制转换模型后，对该缺陷有明显的改进。从表4可以看出：

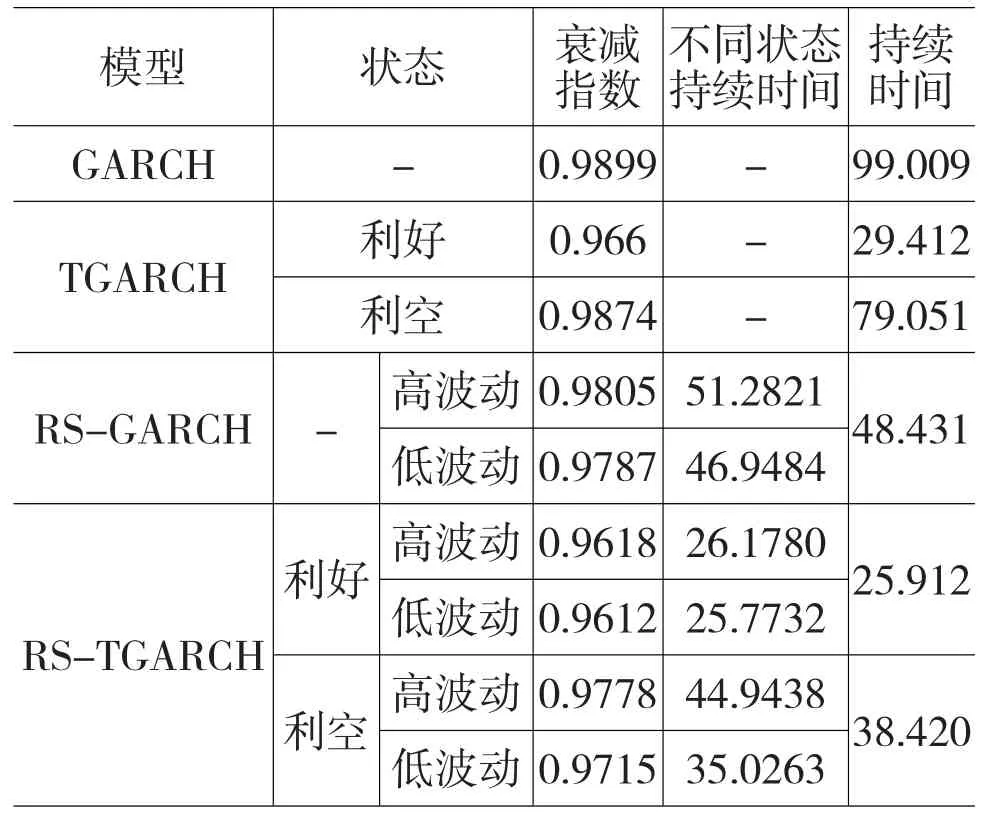
表4 模型持续性比较

其一，对于标准的GARCH模型来说，衰减指数为0.9899，持续时间达99个交易日，明显高于RSGARCH模型的48个交易日，这说明了引入区制转换模型后对伪持续问题有显著改善。

其二，对于TGARCH模型来说，不管是对利好消息或者是利空消息，RS-TGARCH模型均好于一般的TGARCH模型，比如对于利好消息，TGARCH的持续时间为29个交易日，而RS-TGARCH模型的持续时间为26个交易日，有一定程度的改善。

其三，在高波动状态下模型的衰减指数要高于在低波动状态。比如，RS-GARCH模型在高波动状态的持续时间为51天，而在低波动状态为47天。

五、总结与展望

通过对比RS-GARCH模型族和GARCH模型族，一方面发现RS-GARCH模型族对刻画A股市场波动率具有一定的优越性，另一方面也揭示了我国证券市场的一些特征。实证结果表明：

（1）不管是从拟合程度还是从预测误差来看，相对于一般的GARCH模型族RS-GARCH模型族均有明显改善。这是因为RS-GARCH模型族综合考虑了我国证券市场机构体系、制度规范、参与主体等的结构变化，反映在模型中就是预测期数据与拟合期不同的结构问题，因此能够捕捉到各经济变量动态关系，更好地刻画收益率的波动特征。

（2）RS-GARCH模型族有效改善了伪持续现象。RS-GARCH模型族对应一个冲击需要的衰减时间明显缩短，有效改善了伪持续现象。

（3）A股市场存在明显的杠杆效应，利好和利空对于市场的波动率影响有明显差异，对利空消息的反应程度强于利好消息的反应程度。

（4）在高波动状态下，不管是正面消息还是负面消息，对于A股市场波动率的影响都要比低波状态的时间更长。说明低波动状态下投资者的投资行为较高波动状态时更为理性和谨慎。

RS-GARCH模型族不仅探讨了正负消息的非对称影响，同时涉及不同波动状态间的转移概率，以及状态的持续期，因此，RS-GARCH能够较好地刻画我国股市的波动性特征。但文章在比较GARCH模型族和RS-GARCH模型族的优劣时，仅仅考虑了残差正态分布条件下的模型，大量研究和现实表明，我国金融产品非预期收益率并不服从正态分布。因此，探讨不同分布条件下RS-GARCH模型族是有待继续深入的研究方向所在。

[1]Engle Robert F.Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation[J].Econometrica,1982,50: 987-1007.

[2]Bollerslev T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics, 1986,31:307-327.

[3]谢赤，刘潭秋.关于我国外汇市场主要汇率的协整分析[J].预测，2003，（1）：42-45.

[4]赵留彦，王一鸣，蔡婧.中国通胀水平与通胀不确定[J].金融研究，2005，（8）；60-72.

[5]王建军.Markov机制转化模型研究——在中国宏观经济周期分析中的应用[J].数量经济技术经济研究，2007，（3）：39-48.

[6]赵鹏，曾剑云.我国股市周期性破灭型投机泡沫实证研究——基于马尔可夫区制转换方法[J].金融研究，2008，（4）：174-187.

[7]万军，刘思峰，许海靖.基于状态转换GARCH模型的上证综指已实现波动研究[J].工业技术经济，2008，（4）：128-132.

[8]李丽.基于ARMA-GARCH模型的股市量价动态关系研究[J].统计与决策，2011，（4）：144-146.

（责任编辑：贾伟）

1003-4625（2014）02-0078-03

F830.91

A

2013-11-29

郭航（1978-），女，河南驻马店人，经济学硕士，副教授，研究方向：贸易金融方向。