基于Josephus问题的C语言教学设计分析
2014-07-12刘东良
刘东良
C语言教学案例较多,内容涉及较多学科内容,无疑增大了初学者的学习认知负担。为满足C语言的教学需要,以一例"Josephus问题"贯通全部教学内容的方式设计案例。通过Josephus问题的多种变形描述,使其内容覆盖标准C语言的全部知识单元,这样设计能大大的减轻C语言学习者的学习难度,无需费时费力在求解问题本身的理解上,从而使学生能更好地理解、掌握C语言基础知识,一例贯通,举一反三。同时,增加无穷的乐趣和探索精神;加深学习者对C语言知识深度理解和灵活掌握;尽早尽快掌握C语言内容和编程技能,能够进行简单的应用程序设计。
1 Josephus问题和求解
据说古代罗马军队中有一种惩罚习惯:如一个连队因怯懦、反叛或其他理由受到惩罚时,采用"见十去一(decimatio)"的办法进行处罚,即将队伍中凡是站在10的倍数位置上的人处死。有关的事例可以追溯到公元前5世纪。类似的方法在古代的民事战争中被使用,但不一定是"见十去一",也有其他的淘汰比率,如"见二十去一(vicesimatio)"、"见百去一(centesimatio)"等等。Josephus问题就是从此演变而来。
Josephus问题的基本形式是将k个子排成一圈,在这个圈中以某子为起点,m个m个数子,将每次数到的第m子去掉,直到去掉k-n子为止。问保留下来的n子在原来的圈中应排在哪些位置上。
Josephus问题的求解是数学问题,用计算机语言设计程序求解各种约瑟夫及其变形问题具有现代意义和价值。苏格兰数学家Peter Guthrie Tait给出这个问题的通解后,Josephus'Problem,又被称为 Tait's Problem。
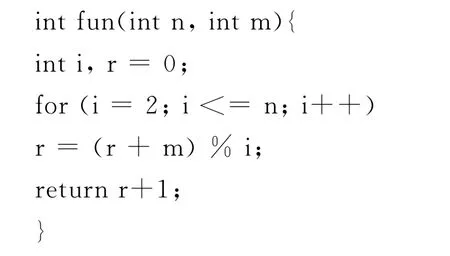
这就是泰特的算法。该算法是一种递推的解法。n是总数,m是报数即间隔数,而i是循环变量,注意它是从2开始的初始条件,r+1为结果又称Josephus Number约瑟夫数。
至今可以检索到许多种算法描述Josephus问题。在这些算法中,主要是利用一维数组或者循环链表进行求解。一般地,假设有一组数据构成一个序列圈(序列的最后一个数据视为与第一个数据相邻接)。要求从第s个数据开始计数,计数到m时弹出该数据,然后从它的下一个数据重新开始计数,计数到m时又弹出该数据,……,直到弹出序列中的所有数据(或只剩下一个或若干数据)为止。对于任意给定的自然数s和m,试求出这组数据的弹出次序。这种描述形式的Josephus问题隐藏了k值,而且对数据类型没有具体要求,数据元素可以是整数、实数、字符或字符串数据,甚至还可以是结构体,通用性好,实用性强。
2 C语言教学单元设计分析
用C语言实现不同Josephus问题的解法,以Josephus问题描述C语言的各知识点,进行一例贯通式教学设计。
2.1 变量和结构化设计分析
以变量代表子,体现变量存储数据的作用。Josephus问题有k个子,起点位置s,m个数子,保留的n子等4个变量。对Josephus问题变形可以扩展更多的变量,比如,在执行程序前,猜哪几个是获胜者,能得到游戏者的成绩,设定一个猜中数w变量;再如,最后必须相邻的两个子ki,ki+1的编号或位置;以及报数时方向顺时针或逆时针;或者将固定m改为不定密码等更多变量。
使用整型数据类型的5个变量实现Josephus。学习while循环,switch、if条件,顺序三种基本结构的应用;小孩使用5个整型变量描述,T是宏,大小不可改变;开始位置,报数,获胜数三个变量;使用#define定义5整型变量。使用C语言中的整型、字符型或者浮点类型仅仅是顺序编号的标示问题。
以变量代表子的解法能深刻揭示Josephus问题的本质,需要C语言的知识也是最富技巧性。如switch和goto语句使得程序运行起来,无限和有限循环while、for语句则揭示计算机擅长的重复工作,变量的顺序则明确C语言的语句顺序执行的重要性。
2.2 数组设计分析
以静态数组定义固定k,限制程序的实用性。k个子用数组表示而且是静态的数组。对于数学问题使用静态数组就可很好解决Josephus问题,数组在理解和使用时都比较简洁方便。利用一维数组求解Josephus问题时,数组的大小(即数组元素的个数)由k值确定。在定义数组之前,必须先给定k值。这个先决条件限制了这类算法的实用性,因为在许多应用领域,事先不知道k的确切值。C/C++语言定义数组的大小,要求使用常量或常变量,为了适应k值,经常需要"大开小用"(不可能使用修改源代码的方法),浪费内存资源。此外,如需要输出字符型数据(如姓名或字符类型的编号等),则需使用二维数组进行描述。利用数组求解Josephus问题的算法比较简练,易于描述。
数组是有序的、线性的、连续的结构,要模拟Josephus问题的环或圈结构,可以使用i=(i+1)%T;构成"圈",即当循环变量i加1与总数相等时,i重新归为0,实现了当沿着数组"直线"向前数时,到最后一个元素后,跳回至第一个元素。注意C语言数组下标从0开始,所以i要加1。另外,还可以使用下面三种表达方式达到同样效果。

修改小孩数组总数可改变T的大小,一般小于50,便于整个程序在较短时间内完成。N+1,N-1,N*m则分别实现数组元素后移,数组元素删除和一次申请所有空间的算法,体现数组的不同应用。
2.3 指针设计分析
动态数组描述不定K,效率高通用性好。k个子用数组表示,是动态的即k子数不定,程序根据输入的不同值计算得到最后结果。在实际程序应用中,或者考虑大数据量运算或者考虑效率,往往采用堆栈动态数组比较合适,既能高效率地执行程序,又能保障结果准确。
用整数i来代替p[i],将初始序列看成一个整数序列存储在向量p中,p[i]出列,将p[i+1],……,p[n]前移一个元素,将p[i]放入p[n]中,最后出列放在p[1]中。指向各编号的position指针形成动态数组,该程序可不限定k子个数,使程序的通用性更好。
2.4 函数设计分析
函数进行模块化设计,理解C语言驱动机制。C语言又称函数语言,其函数设计简洁,没有函数与过程区分。我们可以很容易地将各种设计封装成函数,进行模块化设计;学生也比较容易理解函数的复用意义和模块化好处,难点是函数调用机制的理解。
C语言函数调用遵循嵌套调用的原则。设计一个递归的Josephus问题演示函数调用机制。JosephusRecur递归函数,函数参数依次为k子总数,开始报数位置,间隔报数,猜数和离开时序数。
只有封装成函数,才能直接或间接调用自己,从而形成递归调用。函数模块化设计在许多Josephus问题解法中都有所使用。
2.5 结构设计
结构数组封装K子多元信息。用结构数组封装k子的信息,比如设计小孩或八仙的名称、年龄、生日等不同类型变量。这些成员可以静态或动态设定,从而达到使用不同类型变量和自定义数据类型的目的。同时,理解数组与结构重要区别之一是数组为同类型而结构体可以是不同数据类型的成员。
结构数组并没有使用新的解法,只是比数组增加了必要的辅助信息,这是从简单的样例程序到实用商业程序发展的重要步骤。
2.6 链表设计分析
结构链表模拟Josephus问题过程,直观形象。因为Josephus问题本身是环型,即首尾相联结,循环依次报数。所以利用循环链表进行Josephus问题求解,是一种比较理想的方法,主要体现在:一个循环链表可以被看成是一个圈,可以直接映射问题本身;一般采用动态分配内存的方法建立循环链表(即"按需分配"),可节省存储空间,而且不必事先给定n的值,实用性强;从循环链表中的任何一个结点出发,沿指针指向进行搜索,可以访问到链表中的所有结点;删除链表中相应的结点元素值并释放该结点。释放结点可以缩短链表的长度(即可降低算法的时间复杂度),且有利于存储资源的再利用。但利用循环链表求解Josephus问题的算法相对较复杂,需要一定的基础和技巧。
结构链表的设计主要意图是学习链表的知识内容,直观展示指针的"指向"作用,通过指针的"拉链"、"断链"、"脱链"等显示链表操作过程。
在结构链表的基础上可进一步扩展单向和双向以及循环链表的内容。双向循环链表丰富了Josephus问题多样性。通过结构体包含编号,密码(报数)和方向实现不定报数和不定方向,充分展示Josephus问题趣味性。可带头结点的单链表结构定义和不带头结点的单环链表结构定义设计。
通过指针,C语言可很容易地实现链表,从而更好地理解指针的作用及其重要性。
2.7 队列设计分析
以队列形式反映Josephus问题本质。Josephus问题本质上是一种环型队列,故使用"先进先出"队列结构可更好地实现Josephus问题求解。队列是一种常用的数据结构,一般C语言教学中,没有或很少涉及到。通过Josephus问题理解和掌握队列结构则是很容易达到的。
2.8 栈设计分析
以栈体现函数调用机制。为了展现程序执行时,函数调用机制与"先进后出"的栈特性,设计双栈完成Josephus问题解法,程序运行效果特别形象直观。函数调用机制是现代程序语言特性,掌握堆栈就是掌握程序的驱动原理。
2.9 树设计分析
结构决定效率。以树结构可以提高Josephus程序运行效率。使用Range Tree实现Josephus数的计算是效率比较高的,时间复杂度为O(nlogn),而一般链表为O(n*m),数组为 O(n2)。其中n为总数,m为报数。范围树Range Tree以树状层次结构代替线性结构,提高查找效率,从而提高程序整体效率。
2.10 文件设计分析
文件记录Josephus问题的元数据和过程。C语言的标准输入输出包含了文件操作,是在初学阶段就应该掌握的基础内容。从文件读取Josephus问题的元数据,执行后,将解法过程和结果都保存到文件中去,便于理解。在结果文件中:

第一行5是总数,1是开始位置,3是间隔报数,1是最后一个获胜;第二行至第六行是每次在圈里的号码,竖线后是出圈的号码。
2.11 位运算设计分析
位运算展示Josephus问题特性。通常位运算没有比较好的教学案例,而Josephus问题的一个特例,当m为2即每次向后移动即间隔一个子时,使用位运算则能非常高效地求出约瑟夫数。
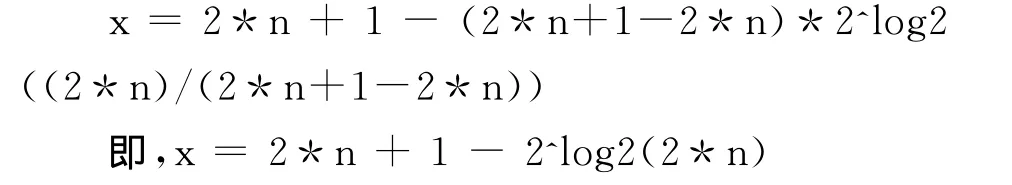
从二进制的角度理解为:将n左移1位(即乘2),然后将最右端设置为1(即加1),最后将左端的1置为0(即减去2*n的向下取的2的幂)。更简单的描述是将n的二进制表示循环左移动一位!如:n为1011001->0110011->1100110。对应代码:
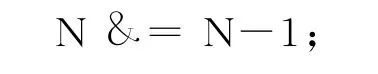
该语句是每次把N二进制最右边的1修改为0,直到最左边的1为止.这种方法也可以用来计算N二进制中1的数目,当N二进制中1的数目比较小的时候算法的效率很高。
2.12 程序测试设计分析
测试是学习计算机语言必须学习的内容之一。测试是检验程序正确性并完善程序。它不同于程序编写、调试,而是对既成的程序,运行特定测试数据(称为测试用例)验证其结果正确性。调试程序阶段主要活动在程序本身的编写过程,执行或简单得到结果后即告结束,而测试刚刚开始。
穷举法测试八仙定座。吕洞宾在2号位不变,其它仙人随机,使用两粒骰子产生点数进行报数,所以有11种可能,吕洞宾是不可能坐上首席的,穷举法测试八仙定座程序正确性。
3 Josephus问题的C语言设计教学效果
实际教学中,整理、设计52个Josephus问题解法,并利用图形函数设计了22个动画演示程序。学生对Josephus问题比较感兴趣,还能主动思考求解Josephus问题的新方法,达到了良好的教学效果。
以Josephus问题典型案例,设计C语言教学内容无疑是一次教学改革和探索,希望能不断改进和完善,使得该研究取得更理想效果。
[1]沈康身.东方约瑟夫问题研究选析[J].自然科学史研究,2003:22(1):60-68.
[2][美]格雷厄姆.具体数学[M].西安:西安电子科技大学出版社,1992:116.
[3]郭世荣.方中通《数度衍》中所见的约瑟夫斯问题[J].自然科学史研究,2002:21(1):49-55.
[4]陈海山.Josephus问题的算法设计与应用研究[J].计算机工程与应用,2007:43(1):61-64.
