幼年赤桉胸径与冠幅、树高、材积的相关性分析

高 灵，王瑞辉，王 睿，谢耀坚，吴志华＊

(1.中南林业科技大学 森林培育国家级重点实验室，湖南 长沙410000；2.国家林业局桉树研究开发中心，广东 湛江 524022)

幼年赤桉胸径与冠幅、树高、材积的相关性分析

高 灵1,2，王瑞辉1，王 睿1,2，谢耀坚2，吴志华2＊

(1.中南林业科技大学 森林培育国家级重点实验室，湖南 长沙410000；2.国家林业局桉树研究开发中心，广东 湛江 524022)

对试验地的1 470株赤桉进行树高、胸径、冠幅的测量，并计算出样木的单株材积。把胸径分别和冠幅、树高及株材积进行相关性分析并且建立数学模型，用SPSS软件对所选模型进行曲线估计。结果表明：其中幂方程的 R2最大，F值亦为最大，说明赤桉胸径与树高的幂关系显著，可确定赤桉胸径与树高的最优回归方程为H=1.804 D0.673。胸径—冠幅，胸径—材积的最优模型分别为CW=0.674 D0.561，V=0.000 161 4 D2.341。分别对3组最优模型进行适应性检验，结果表明：材积的3个最优回归模型预测误差均在±3%以内，方程预测精度较高，可用于估算立木树高、冠幅、材积。

赤桉；胸径；冠幅；树高；立木材积；回归模型

桉树(Eucalyptus)是世界人工造林的第二大树种，因其具有速生丰产、适应性强、用途广、轮伐期短等优良特性，在我国南亚热带作为短周期工业用材林的高产商品材树种已迅速发展起来，且有显著成效[1]。赤桉(E. camaldulensis)是澳大利亚大陆分布最广泛的树种，具有优良的适应性、丰富的遗传多样性。尽管其生长速度、干形的优良程度不及热带、亚热带的主要造林树种尾叶桉(E. urophylla)、巨桉(E. grandis)，但在抗风、耐旱、耐瘠薄方面具有独特的优势，是桉树遗传育种的重要材料，也是世界上栽培较广的桉树种之一[2]。如何对赤桉的各项生长指标进行有效快捷的测量并用于生产研究评估成了一个值得研究的内容。胸径和树高是2个重要的生长性状，也是单株材积计算、林分生长和收获评估中不可或缺的数据[3]。研究树高与胸径的关系意义重大[4-7]。立木材积通常都是利用树高和胸径计算而得[8]。树冠是树木进行光合作用和呼吸作用的重要场所，冠幅和冠长率直接影响树木的生活力和生产力[9]，因此冠幅是林木生长中重要的性状。胸径的测量比较简单，数据可靠，而树高、冠幅和单株材积则相对较难准确获得。在以往的研究中，树高和胸径的相关性已得到多次验证，樊艳文等[10]对北京栓皮栎(Quercus variabilis)林胸径、树高相关生长关系的分析中，证明了各种生境因子和林分因子(地形、土壤、光照、林龄等)对胸径、树高生长关系的幂指数均无显著影响；魏京[11]对胸径、树高的非线性模型进行了拟合性研究；刘敏等[8]研究了辽宁樟子松(Pinus sylvestris)人工林树木胸径与树高、材积的相关关系，得出胸径与材积最优回归方程为V=0.000 165 D2.27886。本研究用胸径分别与冠幅、树高、单株材积进行相关性分析并建立数学模型，为赤桉林地通过测量胸径而推算出树高、冠幅和立木材积的估计值提供依据，同时为赤桉的遗传育种研究和生产提供一定的技术支持。

1 试验地与试验林概况

1.1 试验地概况

试验地在南方国家级林木种苗示范基地内，位于广东省遂溪县岭北镇附近，地理位置为21°30′N，111°38′E，处于湿润大区雷琼热带北缘,为热带北缘季风气候；年均温23.6℃，绝对最低气温2.8℃，绝对最高气温37.0℃，月平均温度18.0℃，夏季降水,年均降水量1 567 mm，5—9月降水占全年的85%，台风频繁，平均每年遭受10级以上台风袭击2 ~ 3次，最大风力大于35 m·s-1[12]。

1.2 试验林概况

2012年5月造林，实际造林为115个家系，每个家系4个重复，共1 470株｡试验设计为完全随机区组，4个区组，株行距2 m×3 m｡面积约14.3 hm2｡本试验林地土壤由花岗岩发育而成，为肥沃的砖红壤，土层厚度大于1 m｡试验林地较为平缓，采用机械全垦整地(垦深30 cm)，铧犁开沟(行距3 m开沟，沟深40 cm)｡

2 研究方法

2014年4月，对赤桉试验林进行树高、胸径、冠幅的林地调查。分别对样木的胸径和冠幅进行东西、南北两个方向的测量，取两个方向的平均值得到胸径和冠幅的值。

2.1 测定方法

以Vertex IV测高测距仪对树高(H)进行测定，分别以卷尺和胸径尺对冠幅(CW)和胸径(D)进行测定。

单株材积(V)采用广西林业勘查设计院总结的广西速生桉单株材积公式，具体如下：

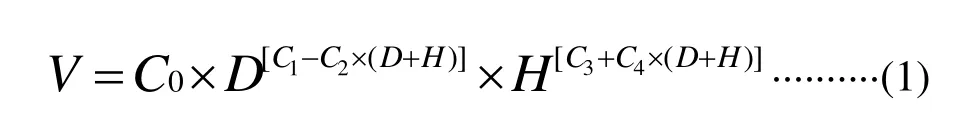
式(1)中的V为单株材积，D为胸径，H为树高，C0=0.000 109 154 150，C1=1.878 923 70，C2=0.005 691 855 03，C3=0.652 598 05，C4=0.007 847 535 07。

2.2 数据整理

通过立木材积公式计算出赤桉单株材积，分别以统计软件SPSS 17(Statistical Product and Service Solutions)作胸径—树高、胸径—冠幅、胸径—材积的散点图，去除个别异常的数据，共得到1 470株赤桉样木用来建立回归模型和模型检验。样木各个变量因子的取值范围分别如下：胸径0.5 ~ 10.0 cm，树高0.9 ~ 9.6 m，冠幅0.20 ~ 4.15 m。为保证建模样木和检验样木在选取时均匀合理，将所有样木按胸径大小排序，每4株家系为1组，抽取每组第1株作为检验样木。剩余样木则选作建模样木。最终总样木为1 470，建模样木和检测样木分别为1 102 (占3/4)和368(1/4)。

2.3 模型的选择

以建模样木胸径为自变量，树高(H)、冠幅(CW)、单株材积(V)分别为因变量，作D-H、D-CW、D-V的散点图。通过对散点图的分析，选取线性函数 y=b0+b1x、对数函数 y=b0+b1lnx、倒数函数y=b0+b1/x、二次函数 y=b0+b1x+b2x2、三次函数y=b0+b1x+b2x2+b3x3、复合函数 y=b0b1x、幂函数y=b0xb1、S函数y=e(b0+b1/x)、生长函数y =e(b0+b1/x)、指数函数y=b0eb1x8个曲线模型作为拟合模型。

2.4 适应性检验方法

将各检验样木实测的胸径值导入所建立的胸径—树高、胸径—冠幅、胸径—材积最优模型中，通过计算，可以得出检验样木的树高、冠幅和材积的估计值。通过对比检验样木中树高、冠幅和材积的实际值，分别计算出各个最优模型的总相对误差、平均相对误差和预估精度，用来确定所建立的最优模型是否符合标准。各指标估计值检验计算按孟宪宇[13]的方法。

3 结果与分析

3.1 D-H回归模型

以建模样木胸径(D)为自变量、树高(H)为因变量，用SPSS 17.0分析软件作D-H散点图(图1)。在SPSS中以所选模型进行曲线估计，当R2最大、F值亦最大时，拟合的模型为最优模型，可确定为赤桉D-H的最优回归方程。通过所选模型对D-H关系在软件中进行拟合，各个拟合曲线的参数见表1。结果显示，所有方程除倒数方程R2外均大于0.700，P值均小于0.05，F值远大于F(1,1 100)=3.84，表明所有的拟合模型均有意义。其中幂方程的R2最大，为0.840，F值为5 758.798，比其他拟合模型的F值都高，说明赤桉D-H的幂关系显著。二次、三次方程的R2均为0.819，但是F值却偏低。线性方程的R2和F值均较高，是回归性比较好的方程。考虑到方程的简捷，取D-H的最优模型为幂方程H=1.804 D0.673。

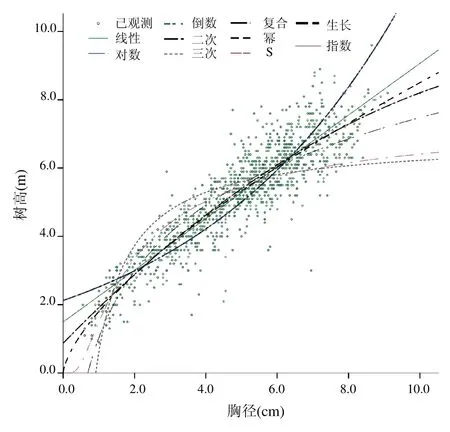
图1 赤桉D-H散点图以及各拟合线

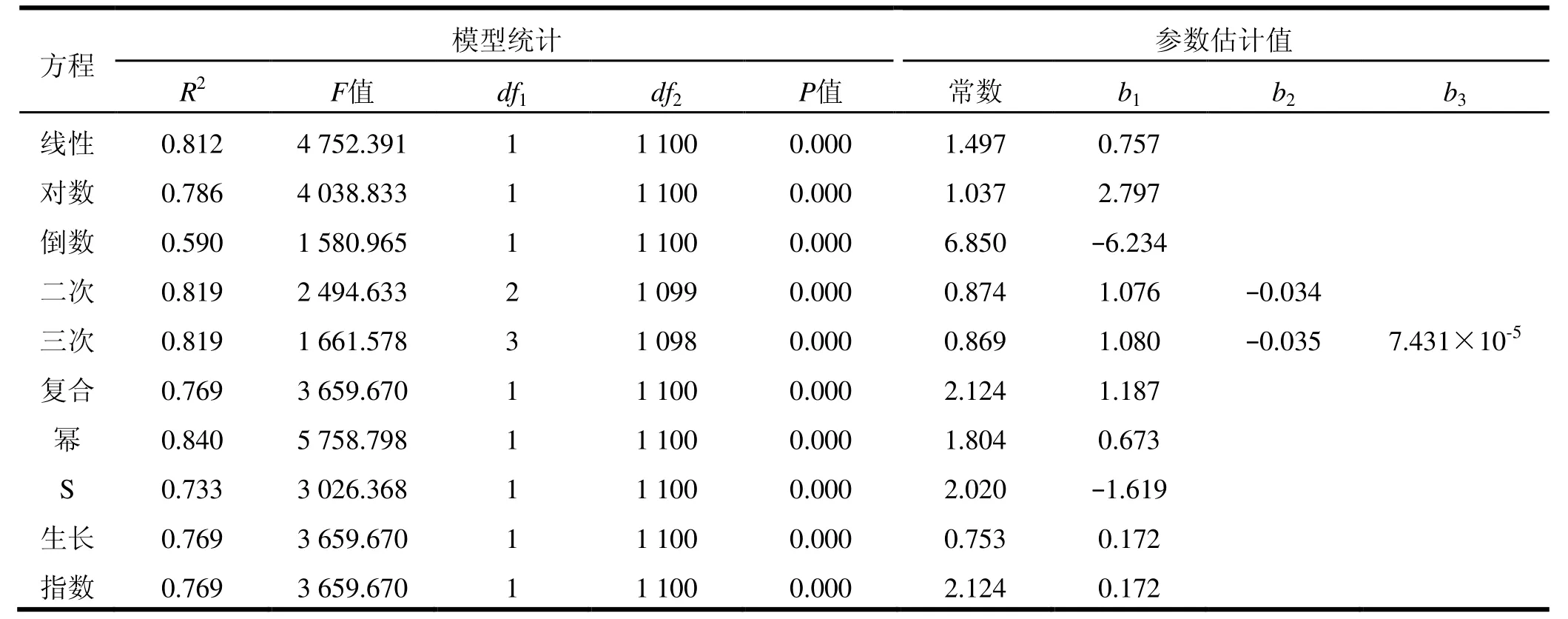
表1 D-H各类模型曲线估计结果

3.2 D-CW回归模型

把建模样木的胸径(D)、冠幅(CW)分别选作自变量、因变量，用SPSS软件作D-CW散点图(图2)。在SPSS中以所选模型进行曲线估计，当R2较大、F值亦大时，拟合的模型的可靠性主要是看方差检验结果(P值)，模型的优选性预测误差小的模型。最后确定赤桉D-CW的最优回归方程。将所选模型对D-CW关系在软件中进行拟合，各个拟合曲线的参数详见表2。结果显示，所有方程除倒数方程R2外均大于0.500，P值均小于0.05，F值远大于F(1,1 100)=3.84，表明拟合出的所有模型均可靠。其中幂方程的R2最大，为0.663，F值为2 161.848，比其他拟合模型的F值都高，说明赤桉D-CW呈显著幂函数关系。仅次于幂关系的是S方程，二者的R2均大于0.6。取D-CW的最优模型为幂方程CW=0.674 D0.561。

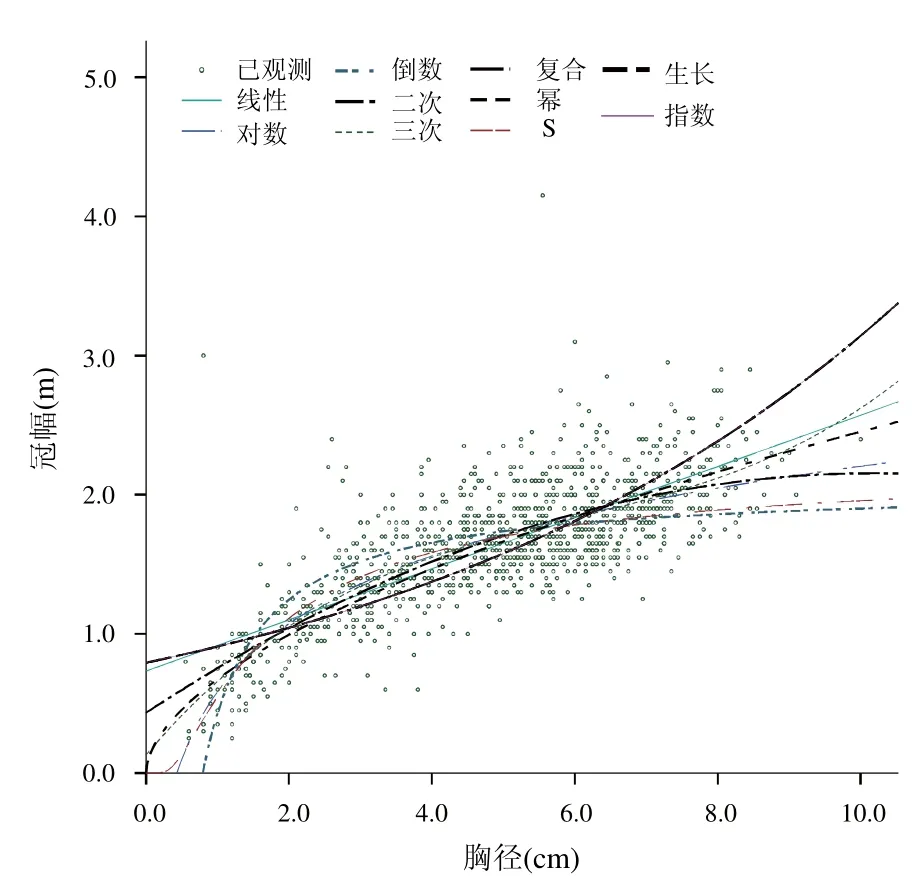
图2 赤桉D-CW散点图以及各拟合线

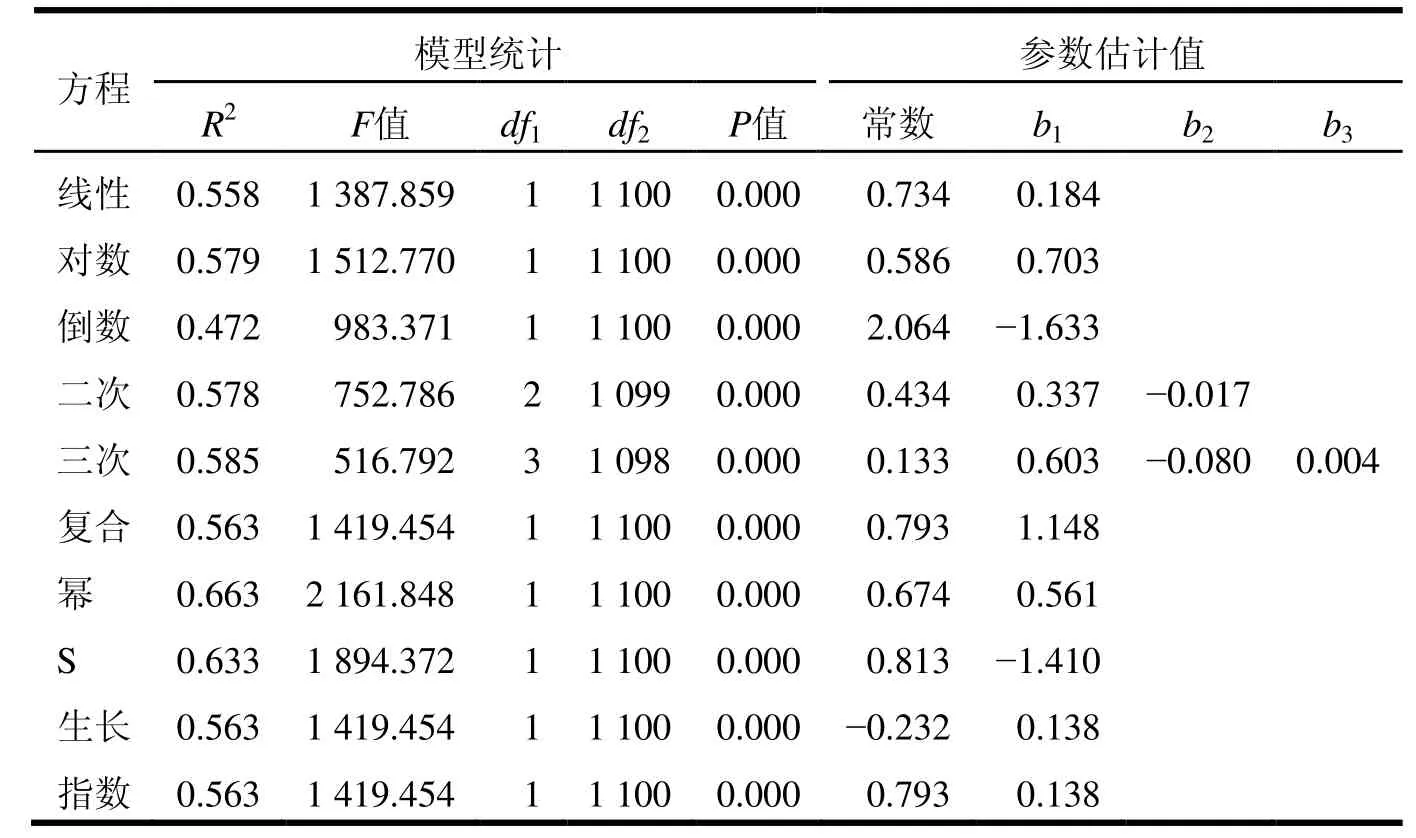
表2 D-CW各类模型曲线估计结果

3.3 D-V回归模型

从图3和表3可知，除了倒数、对数和S曲线外，其他模型的R2均在0.900以上，说明赤桉的胸径(D)与材积(V)之间的相关关系非常紧密。F检验统计量的观察值均大于临界值F(1,109)=3.930，P值均小于0.001，表明所建的模型符合统计学要求。其中幂函数的R2为0.992，最接近1.000，F值为最大，等于128 989.971，显示D-V的幂关系极其显著，幂函数拟合度最好，明显优于其他方程。故选择幂曲线为赤桉D-V最优模型为V=0.000 161 4 D2.341。

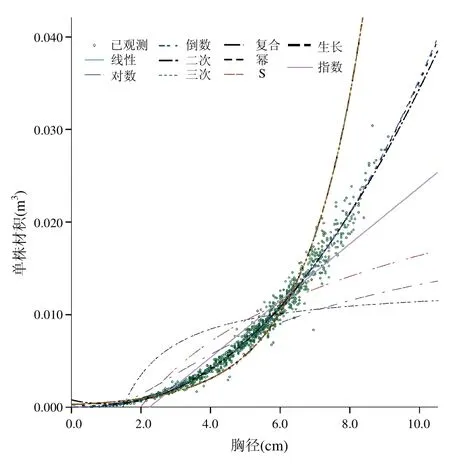
图3 赤桉D-V散点图以及各拟合线

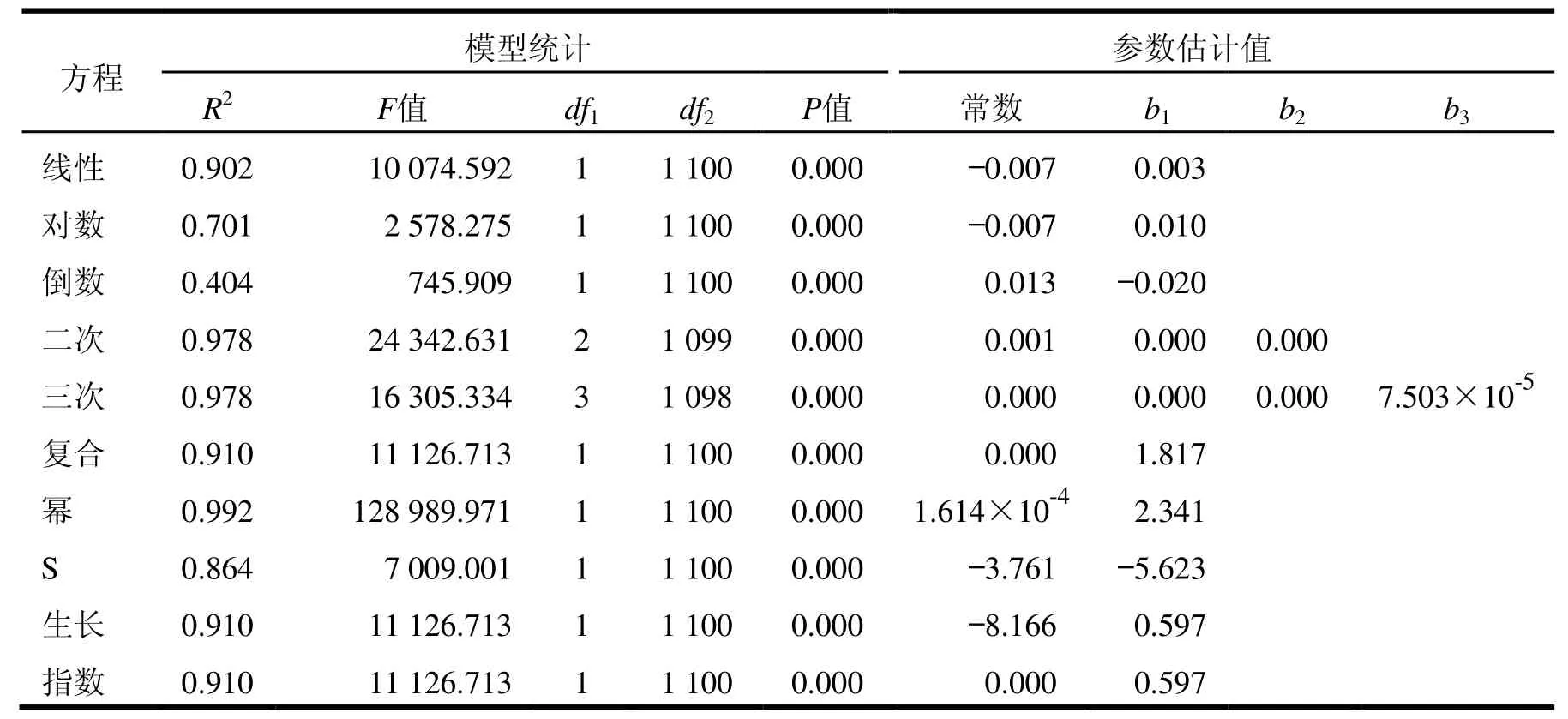
表3 D-V各类模型曲线估计结果

3.4 树高、胸径、冠幅与材积相关性分析

对树高、胸径、冠幅与材积进行相关分析，结果表明(表4)：材积分别与胸径、冠幅、树高成极显著的正相关关系。

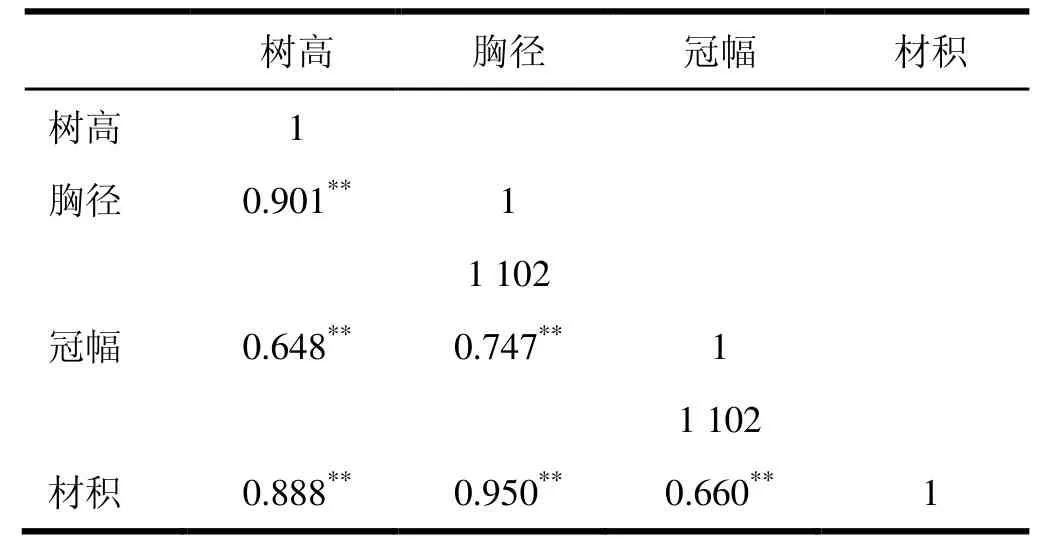
表4 胸径、冠幅、树高与材积两两相关性分析

3.5 模型适应性检验结果

经过验算，赤桉D-H、D-CW、D-V模型精度检验统计指标如表5。结果显示，赤桉D-H模型适应性检验的总相对误差和平均相对误差都在±1%以内，精度高达98.76%，验证了赤桉D-H具有显著的幂函数关系。D-CW的适应性检验误差小于±2%，精度为98.30%，树高和胸径也具有明显的幂函数关系。D-V最优模型的适应性检验总相对误差为0.0 262%，平均相对误差为0.89%，均在±1%以内，精度为98.96%，是精度最高的模型，说明胸径和材积之间的关系十分显著，可以利用赤桉的胸径直接对单株材积进行计算。

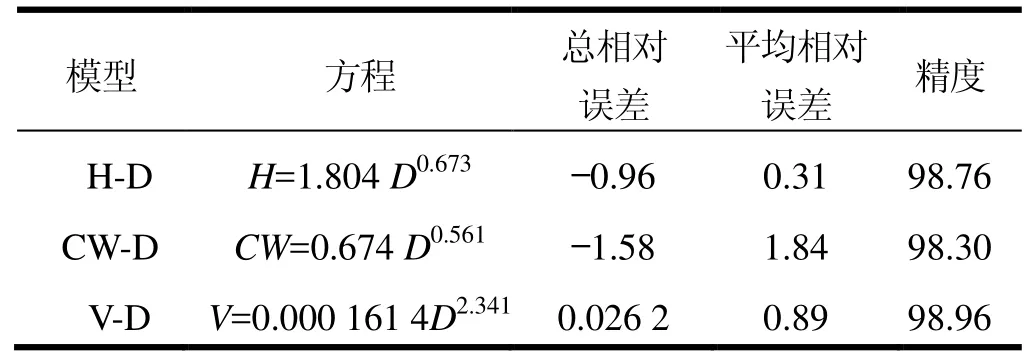
表5 各模型适应性检验评价统计指标 %

4 结论

本研究结果表明，南方国家级林木种苗示范基地内赤桉胸径分别与树高、冠幅、材积呈显著的幂函数关系。D-H、D-CW、D-V幂函数关系分别为H=1.804 D0.673、W=0.674 D0.561、V=0.000 161 4 D2.341。高于林业部颁布的技术规定的误差控制范围[14]，而模型中的误差均在±2%以内，精度在98%以上，模型拟合度相当好，适应性检验误差符合林业部规定范围，可直接运用到当地实际生产中。这些模型不但可为赤桉的遗传研究以及林业生产中估测生长量、采伐量、盗伐量、误伐量等提供依据，也为林业部门提供了一种有效计算赤桉树高、冠幅和材积的方法，即可利用赤桉的胸径—材积模型，编制便于当地使用的赤桉一元胸径材积表，此法较查阅林木二元材积表计算材积更方便快捷[15]。

[1] 刘友全,刘加林,潘天玲.赤桉在湖南的抗寒与生长适应性[J].中南林学院学报,2000,20(3):86-89.

[2] Florence R G.对桉树作为外来树种的感性认识[C]//中国林学会桉树专业委员会.国际桉树学术研讨会论文集.北京:中国林业出版社,1992.

[3] 李海奎,法蕾.基于分级的全国主要树种树高－胸径曲线模型[J].林业科学,2011,47(10):83-90.

[4] 郑传英.四川桤木林分各主要生长因子间相关性研究[J].安徽农学通报,2010,16(17):161-162.

[5] 王晓林,郭斌.柞树树高与胸径相关关系的研究[J].森林工程,2012,28(6):18-21.

[6] 王利,丰震,白世红,等.麻栎树高与胸径相关关系的研究[J].山东林业科技.2005(4):33-34.

[7] 赵敏,丁慧勇.上海水杉树高与胸径关系模式分析[J].上海师范大学学报(自然科学版),2009,38(5):531-535.

[8] 刘敏,张日升,徐贵军,等.辽宁樟子松人工林树木胸径与树高、材积的相关关系[J].防护林科技,2010(1):36-37,41.

[9] 符利勇,孙华,张会儒,等.不同郁闭度下胸高直径对杉木冠幅特征因子的影响[J].生态学报,2013,33(8):2434-2443.

[10] 樊艳文,王襄平,曾令兵,等.北京栓皮栎林胸径-树高相关生长关系的分析[J].北京林业大学学报,2011,33(6): 146-150.

[11] 魏京.林木胸径与树高的关系研究[J].湖北民族学院学报(自然科学版),2014,32(2):190-192．

[12] 张华林,李天会,吴志华,等.不同林分密度对桉树幼林木材材性的影响[J].中南林业科技大学学报,2010,30(6): 85-91.

[13] 孟宪宇.测树学[M].北京:中国林业出版社,1997.

[14] 中华人民共和国林业部.林业专业调查主要技术规定[M].北京:中国林业出版社,1990.

[15] 伍静,吴英,龙楚云,等.尾叶桉地径与胸径、树高、材积相关性分析[J].南方农业学报,2013,44(6):979-983.

Correlation Analyses Between DBH, Crown W idth, Height and Volume of Eucalyptus camaldulensis

GAO Ling1,2, WANG Rui-hui1, WANG Rui1,2, XIE Yao-jian2, WU Zhi-hua2
(1. The Key Lab of Silviculture of State, Central South University of Forestry and Technology, Changsha 410000, Hunan, China; 2. China Eucalypt Research Centre, Zhanjiang 524022, Guangdong, China)

Data were collected from 1 470 Eucalyptus camaldulensis trees including tree height, diameter at breast height and crown w idth measurements. Individual tree volume was calculated from these parameters for each individual tree. Analyses of the correlations between diameter at breast height, crown w idth, tree height and individual tree volume were carried out using SPSS software. The results show that the largest of which R2, F value of the maximum power equation also shows diameter at breast height was significantly higher power relationship can be determined E. camaldulensis optimal diameter and tree height regression equation H = 1.804 D0.673. Similarly come DBH - crown w idth, DBH - volume optimal model was CW = 0.674 D0.561, V = 0.000 161 4 D2.341. To ensure the accuracy of the research and analyses of, respectively, three groups of the far right model for adaptive test results showed that three best regression model to predict volume are in error w ithin ± 3.0%, higher prediction accuracy equation can be used to estimate the standing tree height, crown w idth and volume.

Eucalyptus camaldulensis; DBH; crown w idth; tree height; standing timber volume; regression model

S758.5

A

2014-11-14

广东省林业科技创新专项资金项目 (2011KJCX019);林业重大公益性行业科研专项(201104003)

高灵(1990— )，女，硕士生，主要从事森林培育研究.E-mail:812854076@qq.com

＊通讯作者：吴志华(1974— )，男，硕士，高级工程师，主要从事林木逆境生理研究.E-mail:wzhua2889@163.com