基于遗传算法的2维叶型优化设计

刘龙龙，周正贵，陶胜

（南京航空航天大学能源与动力学院，南京210016）

基于遗传算法的2维叶型优化设计

刘龙龙，周正贵，陶胜

（南京航空航天大学能源与动力学院，南京210016）

为得到具有宽广低损失工作范围的静子叶片，采用基于遗传算法的优化平台对3个不同载荷水平的静子叶栅叶型的型面、安装角及弦长进行优化设计。通过比较3个叶栅优化前后的正常特性线，认为尾缘“负载荷区域”对改善叶栅性能是有益的，且其对叶栅性能的改善效果与叶片载荷有关。结果表明：优化后叶栅性能在设计点和非设计点都有明显改善；叶片表面等熵马赫数分布类似控制扩散叶型，最大载荷点位置前移，叶型前段弯度增加，尾缘出现“负载荷区域”。

静子叶片；压气机；数值优化；遗传算法；负载荷；航空发动机

0 引言

压气机作为航空燃气涡轮发动机的核心部件之一，其增压比和效率将直接影响航空燃气涡轮发动机的推重比、推力和耗油率。目前轴流压气机叶片设计都基于基元级叶栅思想，因此设计性能良好的基元叶型有利于研制高性能压气机叶片。随着计算机计算能力增强和流体力学数值计算技术的发展，采用自动优化方法设计压气机叶片日益受到关注。自动优化方法是将数值优化技术与正问题流场计算相结合，由数学过程替代设计人员经验进行气动优化设计，使得设计过程更加客观、有效。高性能的压气机不仅需要在设计点性能良好，而且需要具有足够的稳定工作裕度，所以在叶片优化设计时，关注的是全工况范围内的性能提升[1]。国内外研究人员分别采用基于梯度方法、单纯形法和遗传算法等数值最优化方法，设计出的叶型不仅在设计点性能优越；同时具有较好的非设计点性能[2-9]。其中国外文献[6-7]优化得到的2维叶型尾缘呈现“负载荷”的特点。

本文采用基于遗传算法的叶片优化平台对3个不同载荷水平的静子叶栅叶型进行优化设计，以期得到不仅在设计点性能良好，而且具有较好非设计点性能的优化叶型。

1 数值最优化方法

基于遗传算法的叶片优化平台是指将遗传算法与正问题流场计算相结合，采用优化控制理论寻找最优叶型[8,10]。本文提到的叶片优化平台主要包括数值最优化、正问题流场计算、叶型参数化生成及目标函数设定4个模块。叶片优化设计流程如图1所示。

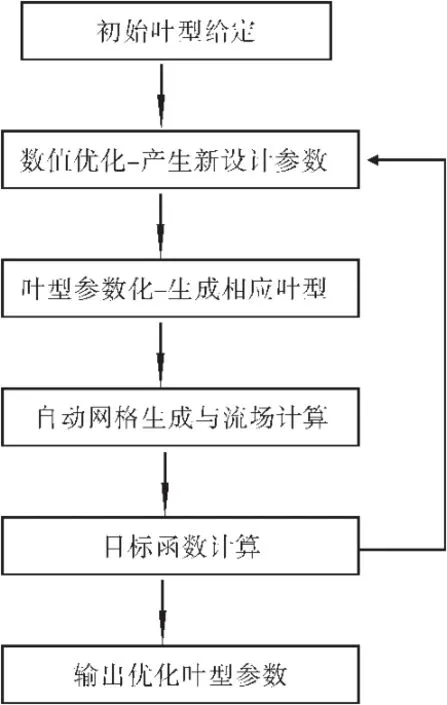
图1 叶片优化设计流程

1.1 叶型参数化方法

叶型参数化是指采用对原始叶型型线附加修改量的方法[10]，运用有限个设计参数来描述叶型，以便控制修改叶型，将叶型压力面和吸力面的修改量定义为

式中：Wk为权重系数；x为设计变量；N为设计变量数；形状函数fk(x)定义为

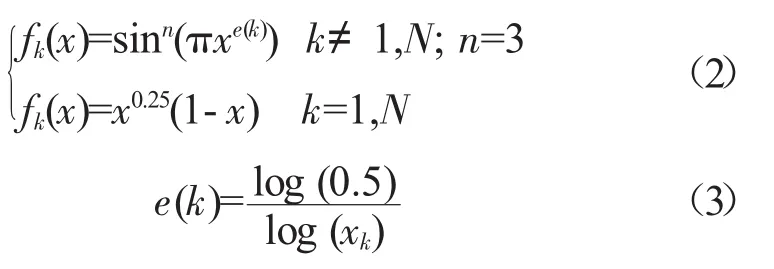
式(3)中xk是指形状函数峰值点所在位置。吸力面和压力面xk取值一致，分别取0.05、0.10、0.25、0.45、0.65、0.80、0.90、0.95。除将上述叶型的型面修改量作为设计参数外，弦长和安装角也作为设计参数，以增加叶型的寻优空间，弦长相对于初始弦长的变化范围为[-0.5,0.5]，安装角相对初始安装角的变化范围为[-10°,10°]。

1.2 流场计算方法

采用基于遗传算法的叶片优化平台进行2维叶型优化设计时，需反复进行正问题流场计算。流场计算需精度足够才能保证优化设计具有可靠的结果。为缩短流场计算所需时间，优化平台流场计算程序采用任意曲线坐标系下的N-S方程，有限体积空间离散，4步龙格-库塔时间推进法求定常解，湍流模型采用B-L模型[11]。网格采用壁面正交H型网格，靠近壁面处网格进行加密处理，如图2所示。通过与商用软件Numeca的计算结果比较，对该流场计算程序的计算精度进行了验证。计算时保证叶型、边界条件完全一致，结果对比如图3所示。结果表明：该流场计算程序具有较高的可靠性，可用于自动优化设计的流场计算。

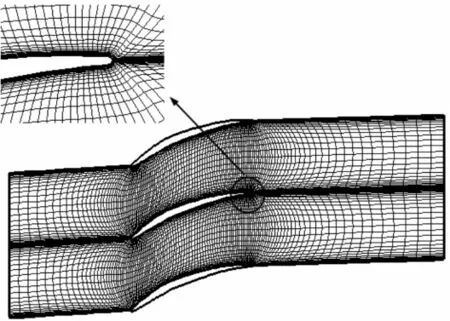
图2 流场计算网格

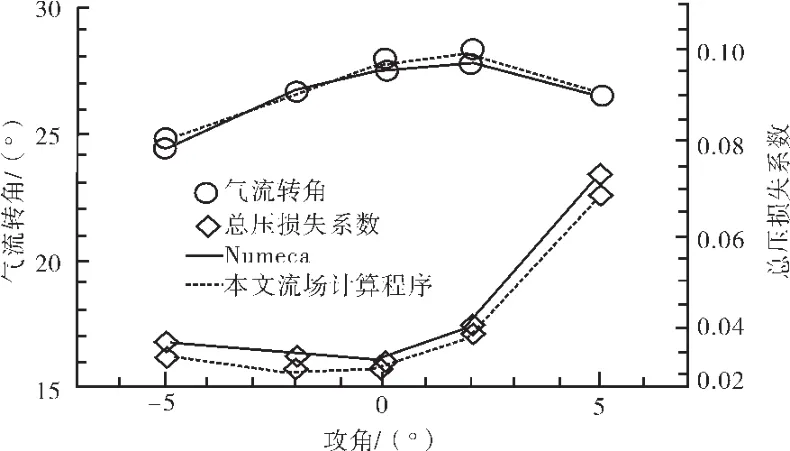
图3 流场计算程序精度验证

1.3 目标函数设定

遗传算法可以将多目标问题通过权重系数转化成单目标进行寻优[11]，目标函数定为

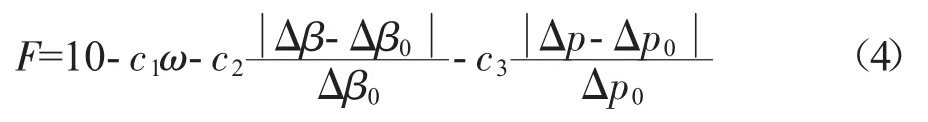
式中：c1、c2、c3为目标函数的权重系数；ω为设计工况下的总压损失系数；Δβ、Δβ0分别为设计工况下的气流转角和目标气流转角；Δp、Δp0分别为设计工况下的静压比和目标静压比。

在设计攻角下，当总压损失系数最小，气流转角和静压比达到目标值时，目标函数取得最大值，对应的叶型为最优叶型。

2 优化结果分析

本文分别对3个不同载荷水平（对于亚声速叶型载荷大小可由气流转角大小表征）的静子平面叶栅进行叶型优化，优化以在设计点处达到目标气流转角且总压损失系数最小为目标。为便于区分，分别称3个叶栅对应的原始叶型为原始叶型Ⅰ、Ⅱ、Ⅲ；对应的优化叶型称为优化叶型Ⅰ、Ⅱ、Ⅲ，见表1。

表1 原始叶栅相关参数

2.1 优化前后叶栅设计点性能对比

在设计点的叶栅性能参数（见表2）表明，3个优化叶型在气流转角与目标气流转角基本一致的情况下，总压损失系数减小明显。

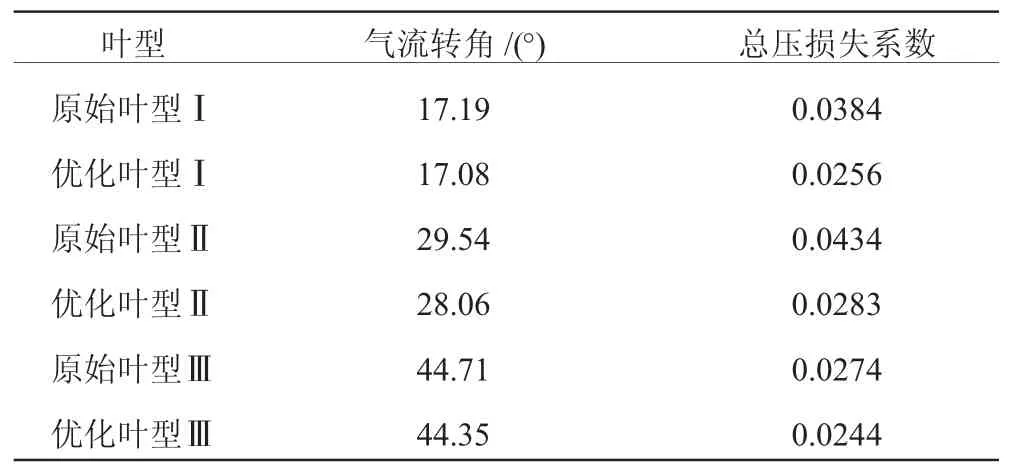
表2 设计点性能参数

3个优化叶型与各自原始叶型的比较如图4所示。从图4中可见，3个优化叶型型面相对各自原始叶型有如下变化趋势：优化叶型前段相对原始叶型弯度增大，而靠近尾缘段变得相对平直；压力面的尾缘处有1段上翘区域，压力面型线在这段区域由“上凹”渐变为“下凸”。原始叶型Ⅰ、Ⅲ在优化后弦长和安装角变化不大，而原始叶型Ⅱ在优化后弦长和安装角变化很大。原因在于原始叶型Ⅰ、Ⅲ性能较好，其几何参数本身较为合理，因此优化后叶型几何参数变化不如原始叶型Ⅱ剧烈。

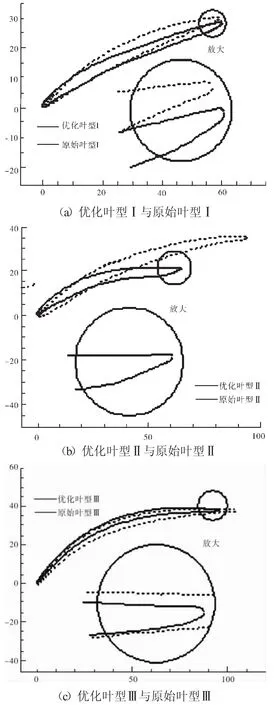
图4 优化叶型与原始叶型的比较

设计点处3个叶型优化前后的叶型表面马赫数分布如图5所示。由于优化前后叶片弦长有变化，为方便比较优化对载荷分布影响，横坐标采用相对弦长。从图5中可见，3个优化叶型的最大载荷点位置相对原始叶型都前移，优化叶型前缘区域载荷增大；优化后叶型吸力面表面马赫数分布与控制扩散叶型类似[12-13]，在3个优化叶型的尾缘都出现了“负载荷区域”。原始与优化叶型采用同一流场计算程序，且计算时保证网格划分方式和数量一致。在采用相同计算程序和网格计算的前提下，原始叶型并没有“负载荷区域”，而仅优化叶型出现“负载荷区域”，表明出现“尾缘负荷的交叉”并不是计算误差所引起的。在文献[6-7]中，O.Lotfi和Bo Song也分别得出与本文类似的载荷前移、尾缘存在“负载荷区域”的优化叶型，且叶型优化后性能改善得到了验证。

载荷分布的变化趋势与叶型型面变化是相关联的，体现在优化叶型前段弯度增加，气流流过优化叶型前段的转角大于流过原始叶型，相应的其前段载荷也会增大；当亚声速气流流过压力面型线由“上凹”渐变成“下凸”的区域时，贴近压力面表面的流管先收缩后扩张，其内气流先加速后减速，体现在图5中就是尾缘形成了“负载荷区域”。

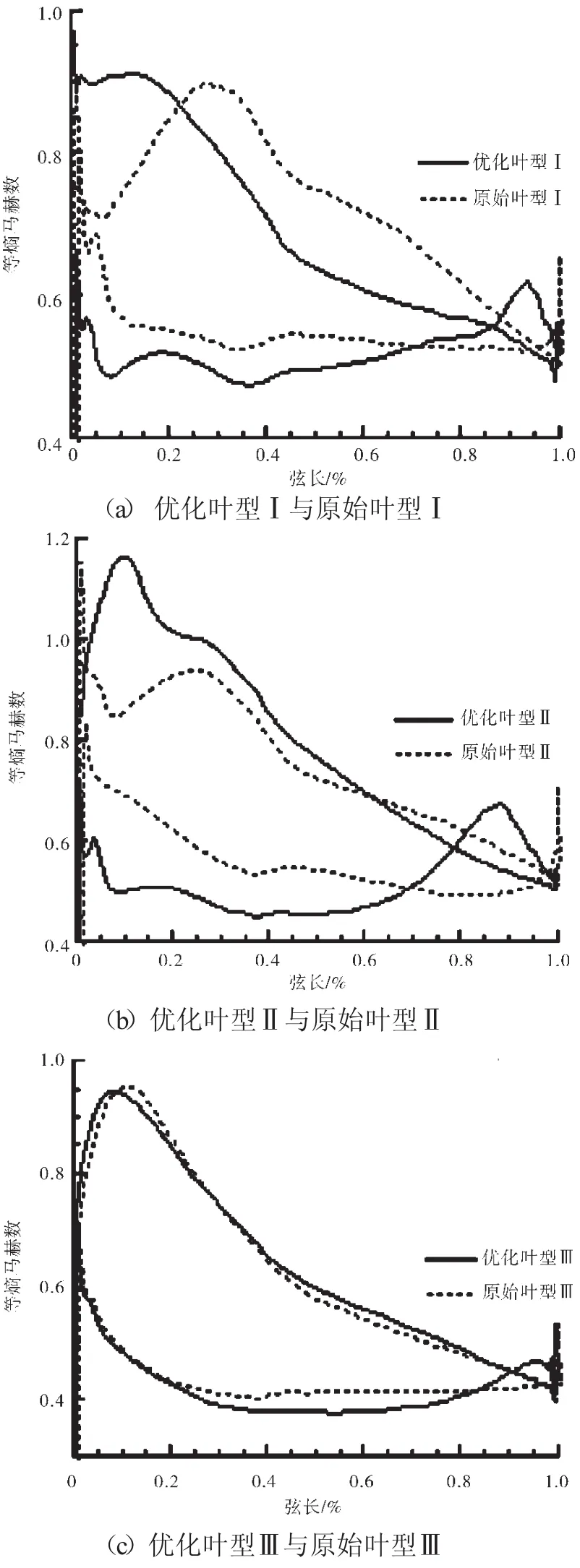
图5 叶片表面等熵马赫数分布

从图5中还可见，优化叶型尾缘“负载荷区域”越大，其前缘区域载荷增大越多，与优化目标有关。本文优化目标之一是优化前后叶片载荷基本不变（即气流转角基本不变）。在优化叶型尾缘出现“负载荷区域”的情况下必然需要增大前缘区域的载荷以保证叶型整体载荷基本不变，且尾缘“负载荷区域”越大，前缘区域载荷增大越多。最终可能导致原始叶型无超声区而优化叶型前缘区域出现，如图5（b）所示。

载荷前移和“负载荷区域”会影响叶型表面附近附面层发展，进而影响叶栅性能。由于载荷前移和“负载荷区域”对3个优化叶型压力面附近附面层发展影响规律是相似的，为避免重复，只给出了原始叶型Ⅱ及优化叶型Ⅱ对应的叶栅在设计点处通道马赫数等值线，如图6所示。从图6中可见，由于优化叶型前半段弯度增大，载荷前移，使得优化叶型压力面前段附面层较原始叶型迅速，导致叶型损失变大；但由于尾缘“负载荷区域”的存在，对应区域压力面表面附近的流体局部加速，附面层发展明显被抑制，附面层相比原始叶型变薄，尾迹区明显减小，有利于减少叶型损失[14]。图6验证了前文关于流体流经压力面型线由“上凹”渐变成“下凸”区域时的流态分析，表明尾缘“负载荷区域”确为叶型型面所引起的物理现象。

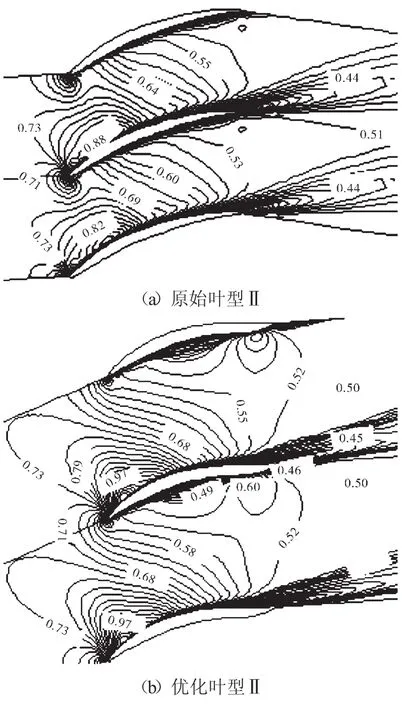
图6 叶栅通道内马赫数等值线分布

2.2 优化前后叶栅全工况性能比较

压气机的工作状态变化时，叶片的进口气流角和马赫数等参数也随之变化，因此，需要叶栅优化后不仅在设计点性能提升，而且在非设计点也具有良好的性能。叶栅的正常特性线如图7所示。从图7中可见，在全工况范围内，3组叶栅优化前后的气流转角都很接近，也就是说优化前后叶片载荷基本不变；叶型优化后3组叶栅不仅设计点性能与原始叶栅相比有明显提高，而且非设计点性能也得到改善。

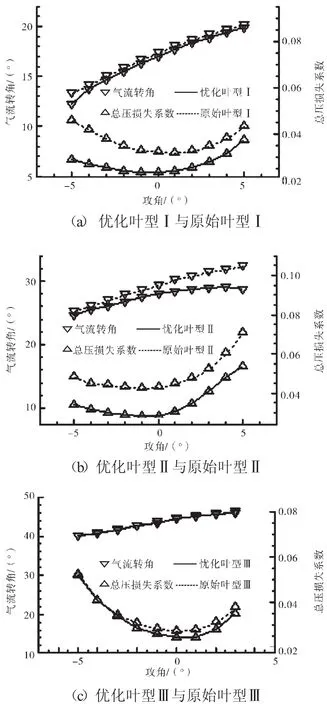
图7 叶栅的正常特性线

优化前后静压比的对比如图8所示。从图8中可见，叶型优化后3组叶栅在全工况范围内的静压比均有增大。对于静子叶型来说，其增压能力与气流转折角是正相关的，由于叶型优化后气流转角基本不变，而优化后叶型损失减少，因而相应叶型的增压能力提高。

从图7中可见，3个叶栅优化后在负攻角下的性能提升幅度不一致，为便于研究，定义某一点处的总压损失系数下降幅度为

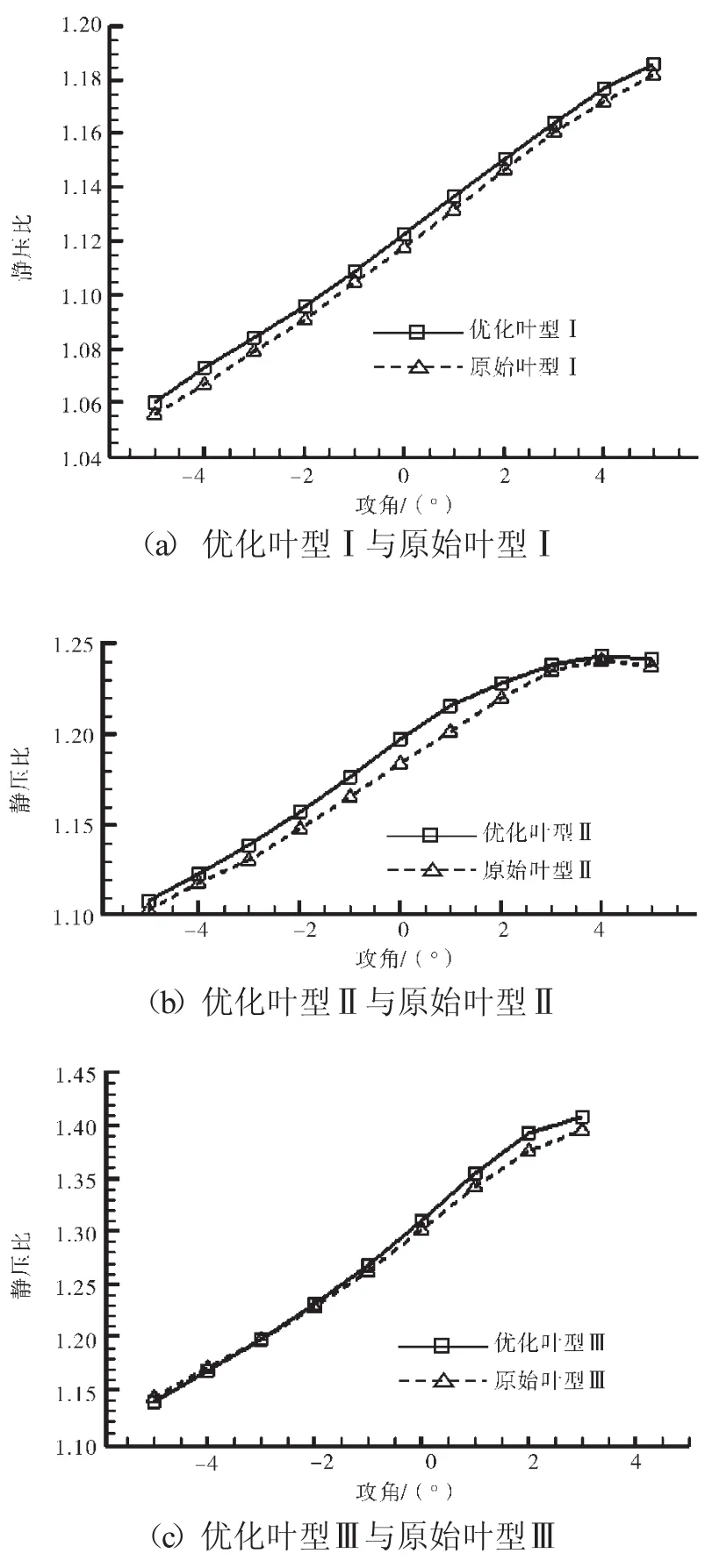
图8 优化前后静压比比较

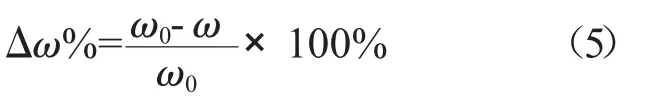
式中：ω0、ω分别为该点处原始、优化后叶栅的总压损失系数。

从图8中还可见，在全工况范围内，优化叶型Ⅰ、Ⅱ对应的总压损失系数减小幅度大于优化叶型Ⅲ的，这是由于优化叶型Ⅲ对应的原始叶栅性能已较好，优化后性能难以大幅提高。

性能改善与攻角关系如图9所示。从图9中可见，当攻角为负时，随着负攻角增大，优化叶型Ⅰ对应的总压损失系数减小幅度明显增加，Ⅱ对应的总压恢复系数减小幅度与设计点处相比略有下降但相差不多；而Ⅲ对应的总压恢复系数减小幅度明显减小。即呈现叶片载荷越小，负攻角下叶栅性能改善越显著的规律。叶片前段弯度增加和尾缘“负载荷区域”对叶型损失不同的影响规律是造成上述现象的原因。

当攻角由零度变为负时，叶型压力面附面层会变厚甚至出现分离，损失增加[15]。且一般来说叶型弯度越大，负攻角下压力面附面层发展越快、越容易出现分离；而本文优化叶型出现的尾缘“负载荷区域”能抑制压力面附面层发展，推迟压力面附面层分离，对减小负攻角下的损失是有益的。下面针对2个不同载荷水平的叶型加以分析（图9）。

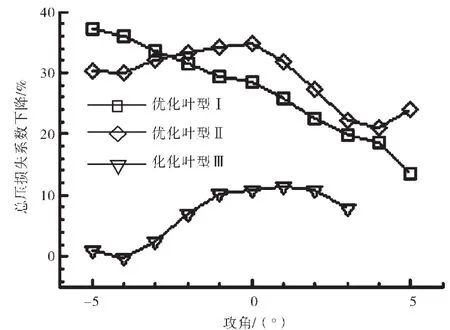
图9 性能改善与攻角关系

对于载荷较小的情况（如原始与优化叶型Ⅰ），虽然优化后叶型前段的弯度有所增加，但弯度仍然较小，对压力面附面层发展影响不大，此时，尾缘“负载荷区域”对压力面附面层发展的抑制起主要作用。负攻角越大，“负载荷区域”对优化叶型Ⅰ压力面附面层发展的抑制效果相比原始叶型Ⅰ就越明显，优化叶型Ⅰ对应叶栅的损失随负攻角变大而增加的速度也就比原始叶型Ⅰ所对应叶栅慢。因此，优化后叶栅的总压损失系数减小幅度随负攻角增大而增加。

对于载荷较大的情况（如原始与优化叶型Ⅲ），由于叶型前段弯度大，对应区域的附面层发展也较快，此时，尾缘“负载荷区域”抑制压力面附面层发展所减小的损失无法抵消由于叶型弯度增大所带来的损失。优化叶型Ⅲ由于前段弯度大于原始叶型Ⅲ，其压力面前段附面层发展更快；且负攻角越大，弯度增加带来的附面损失增长也越快，优化叶型Ⅲ对应叶栅的损失随负攻角变大而增加的速度也就比原始叶型Ⅲ所对应叶栅快。因此，优化后叶栅的总压恢复系数减小幅度随负攻角增大而减少。

通过以上优化结果分析可以发现，表面压力分布出现载荷前移、尾缘“负载荷区域”的这一类叶型有益于改善叶栅性能。特别对于弯度不大的叶型，在负攻角下性能的提升效果尤为突出。

3 结论

（1）采用基于遗传算法的优化平台对静子平面叶栅优化，优化后叶栅不仅在设计点性能改善明显，而且在非设计点同样具有良好的性能。

（2）优化后叶型前段弯度增加，压力面尾缘上翘；载荷分布前移，吸力面表面压力分布与控制扩散叶型类似，且尾缘出现“负载荷区域”。

（3）尾缘“负载荷区域”能有效抑制压力面表面附近附面层发展，对提升负攻角下的叶栅性能有益；当叶型弯度较小时，提升效果尤为明显。

[1]周正贵.压气机/风扇叶片自动优化设计的研究现状和关键技术[J].航空学报，2008，29（2）：257-266. ZHOUZhenggui.Current situations and key techniques of automatic aerodynamic design of compressor/fan blades[J].Acta Aeronautica et Astronautica Sinica，2008，29（2）：257-266.（in Chinese）

[2]Frank S，Beat R，Casey M，et al.Design of industrial axial compressor blade sections for optimal range and performance [J].Journal of Turbomachinery，2004，126（2）：323-331.

[3]Benini E，Toffolo A.Development of high performance airfoils for axial flow compressors using evolutionary computation[J]. Journal of Propulsion and Power，2002，18（3）：544-554.

[4]Koller U，Monig R，Kusters B，et a1.Development of advanced compressor airfoils for heavyduty gas turbines-Part I:design and optimization[J].Journal of Turbomachinery，2000，122（3）：397-405.

[5]Kusters B，Schreiber H A，Koller U，et al.Development of advanced compressor airfoils for heavyduty gas turbines-Part II:experimental and theoretical analysis[J].Journal of Turbomachinery，2000，122（3）：406-415.

[6]Lotfi O，Teixeira J A，Ivey P C，et al.Aerodynamic optimization of industrial fan blade cascades[R].ASME 2005-GT-68385.

[7]Song Bo，Wing F N.Performance and flow characteristics of an optimized supercritical compressor stator cascade[R].ASME 2005-GT-68569.

[8]汪光文，周正贵，胡骏.基于优化算法的压气机叶片气动设计[J].航空动力学报，2008，23（7）：1218-1224. WANG Guangwen，ZHOU Zhenggui，HU Jun.Aerodynamic design of compressor blade using optimization algorithm[J].Journal of Aerospace Power，2008，23（7）：1218-1224.（in Chinese）

[9]周正贵，邱名，徐夏，等.压气机/风扇二维叶型自动优化设计[J].航空学报，2011，32（11）：1987-1997. ZHOUZhenggui，QIUMing，XU Xia，et al.Automatic optimization design of compressor/fan 2D blade profiles[J].Acta Aeronautica et Astronautica Sinica，2011，32（11）：1987-1997.（in Chinese）

[10]周正贵.高亚声速压气机叶片优化设计[J].推进技术，2004，25（1）：58-61. ZHOUZhenggui.Optimizationofhighsubsonicaxial compressor blades[J].Journal of Propulsion Technology，2004，25（1）：58-61.（in Chinese）

[11]周正贵.混合遗传算法及其在叶片自动优化设计中的应用[J].航空学报，2002，23（6）：571-574. ZHOUZhenggui.Compositegeneticalgorithmandits application to automatic optimization of turbomachinery blade [J].Acta Aeronautica et Astronautica Sinica，2002，23（6）：571-574.（in Chinese）

[12]钟兢军，王会社，王仲奇.多级压气机中可控扩散叶型研究的进展与展望-（第一部分）：可控扩散叶型的设计与发展[J].航空动力学报，2001，16（3）：205-211. ZHONG Jingjun，WANG Huishe，WANG Zhongqi.Development and prospect of controlled diffusion airfoils for multistage compressor-PartⅠ:design and development of controlled diffu sion airfoils[J].Journal of Aerospace Power，2001，16（3）：205-211.（in Chinese）

[13]刘波，周新海，严汝群.轴流压气机可控扩散叶型的数值优化设计[J].航空动力学报，1991，6（1）：9-12，89. LIU Bo，ZHOU Haixin，YAN Ruqun.Numerical optimization program for designing controlled diffusion compressor blading [J].Journal of Aerospace Power，1991，6（1）：9-12，89.（in Chinese）

[14]吴国钏，邢宗文.附面层理论[M].北京:航空工业出版社，1989：199-202. WU Guochuan，XING Zongwen.Boundary layer theroy[M]. Beijing：AviationIndustryPress，1989：199-202.（in Chinese）

[15]胡骏，吴铁鹰，曹人靖.航空叶片机原理[M].北京：国防工业出版社，2006：52-53. HU Jun，WU Tieying，CAO Renjing.Principle of aeroengine blade[M].Beijing：National Defense Industry Press，2006：52-53.（in Chinese）

Optimization Design on 2D Blade Profiles Based on Genetic Algorithm

LIU Long-long,ZHOU Zheng-gui,TAO Sheng
（College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China）

In order to get stator blades with low loss in a wide range of attack angle,three stator blades profiles of different load levels were optimized by the genetic algorithm.According to contrasting the normal characteristic behind and after three cascades optimized,the negative load region on the trailing edge was significant for improving the cascade performance,which affects the optimized results and blade loadings of cascade performance.The results show that the optimized cascade performance has obvious improvements for design conditions and off design conditions.The distributions of isentropic Mach number on the blade surfaces is similar with the controlled diffusion profiles,the position of maximum loads moves forward,camber increased in front of blades,and the“negative load region”appears on the trailing edge.

stator blade;compressor;numerical optimization;genetic algorithm;negative load;aeroengine

V 232.4

A

10.13477/j.cnki.aeroengine.2014.05.010

2013-04-18

刘龙龙（1988），男，硕士，研究方向为叶轮机气体动力学；E-mail:longll211@163.com。

刘龙龙，周正贵，陶胜.基于遗传算法的2维叶型优化设计[J].航空发动机，2014，40（5）：50-56.LIU Longlong,ZHOU Zhenggui,TAO Sheng. Optimization design on 2Dblade profiles based on genetic algorithm[J].Aeroengine，2014，40（5）：50-56.