一种基于滑模非奇异的反舰导弹导引律的设计与仿真

周源，雷军委，薛于廷

（海军航空工程学院a.7系；b.控制工程系，山东烟台264001）

一种基于滑模非奇异的反舰导弹导引律的设计与仿真

周源a，雷军委b，薛于廷b

（海军航空工程学院a.7系；b.控制工程系，山东烟台264001）

提出了一种反舰导弹滑模非奇异导引律。根据反舰导弹弹道的运动学分析方法，建立了弹目相对运动的数学模型。在非奇异理论的基础上，推导出具有带落角约束的滑模非奇异导引律。通过仿真，表明了该导引律能同时满足脱靶和落角的性能指标，具有优良的鲁棒性，脱靶量更小，精度更高。相比传统的比例导引律，具有更强的实用性和有效性。

反舰导弹；导引律；滑模；非奇异；鲁棒性

在反舰导弹导引律的设计上，以往都采用比例导引律。然而，当存在目标机动时，为截获目标，比例导引律需要大的加速度命令，这样一来可能导致脱靶。在某些情况下，发射导弹不仅希望获得最小脱靶量，而且希望能以期望的攻击角度命中目标[1-3]。近年来，由于滑模变结构控制系统固有的强鲁棒性，加之控制算法比较简单，变结构控制理论越来越多被应用于导引律设计。变结构控制系统的动态性能主要是由预先选定的滑模面来决定的。一般情况下，选择线性的滑动超平面是变结构控制理论中最为常见的情形。这个线性的滑动超平面能够确保系统轨迹在到达滑动模态阶段以后，滑动模态的运动是渐近稳定的或者说跟踪误差渐近地收敛到零，并且渐近收敛的速度可以通过选择滑模面参数矩阵来任意调节。在滑动平面的设计中引入非线性函数，突破了普通滑模控制在线性滑模面条件下渐近收敛的特点，使得在滑模面上的跟踪误差能够在有限时间内收敛至零[4-5]。

1 导引系统模型

根据反舰导弹弹道的运动学分析方法，假设导弹与目标的相对运动方程可以用定义在攻击平面内的极坐标参数r、q的变化规律来描述[6-7]。假设某一时刻，目标位于T点，导弹位于M点。连线----MT称为目标瞄准线（简称为目标线或视线）。图1描述了导弹与目标之间的相对运动关系。图1中：r为导弹相对目标的距离，导弹命中目标时r=0；q为目标线与基准线之间的夹角，即目标方位角（简称目标线角），若从基准线逆时针转到目标线上，则q为正；σ、σT分别为导弹、目标速度矢量与基准线之间的夹角，称为导弹弹道角和目标航向角，当攻击平面为铅垂面时，σ就是弹道倾角θ，当攻击平面为水平面时，σ就是弹道偏角ψν；η、ηT分别为导弹、目标速度矢量与目标线之间的夹角，相应称之为导弹速度矢量前置角和目标速度矢量前置角（简称为前置角）；Φ为相对航向误差角（弹目相对速度方向与弹目视线方向之间的夹角）；v、vT、vre分别为导弹速度、目标速度和导弹—目标相对速度。

图1 导弹与目标的相对运动关系示意图Fig.1 Schematic diagram of m issile and target of the relative motion relationship

由图1可得到如下的弹目相对运动方程组：

式中，vr、vq分别为导弹与目标的接近速度和视线法向速度[8-10]。

考虑到导弹、目标加速度只改变速度方向，则有：

对式（1）两边同时求导，整理可得：

2 带落角约束的非奇异变结构导引律设计

本文在文献[5]的基础上，考虑了落角约束。起初设计了一种带落角约束的变结构导引律，但是，该导引律的控制量存在奇异问题。文献[6-7]的研究表明，基于零化相对航向误差角（弹目相对速度与弹目视线之间的夹角）的导引律适用于任意初始导弹弹道角和目标航向角。因此，本文重新设计了滑模面，基于零化相对航向误差角[11]，进一步设计了一种带落角约束的非奇异变结构导引律。

2.1 变结构导引律设计对式（1）求导，同时联立式（2），可得：

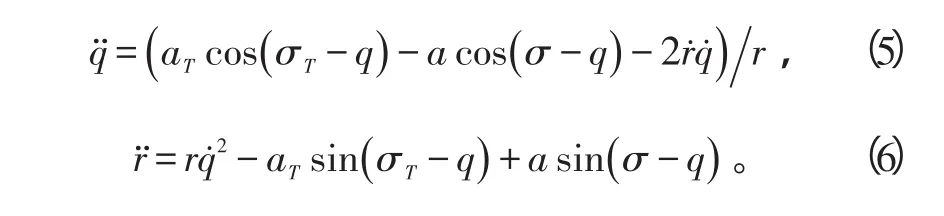
将r、q-qm、q˙和r˙作为状态变量，则有

对上式（7）求导，则有

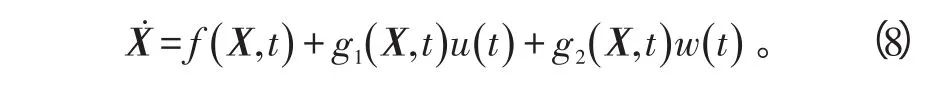
将目标加速度项aT视作干扰，且假设有界，即有0≤‖w(t)‖≤N，N正常数。

在反舰导弹攻击舰艇目标时，只须控制视线角速度趋于0，即可在理论上实现零脱靶量，考虑到落角约束，故选取滑模面

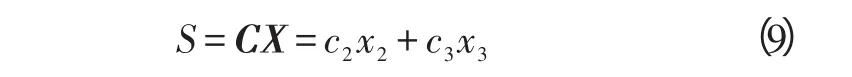
式中，C=[c1c2c3c4c5],ci(i=1,2,…,5)为正常数[12]。

2.2 非奇异变结构导引律设计

在图1中，Φ定义相对航向误差角，考虑其物理意义，则有：

由式（11）可知，当Φ=0时，可推出r=0或者q˙=0。因此，Φ=0可保证导弹命中目标。

联立式（10）和式（11），可得：

由图1可得

已知

联立式（14）和式（15），可得

将式（12）代入式（16），得

选取滑模面为

式中，C=[c1c2c3c4c5],ci(i=1,2,…,5)为正常数[13-14]。

变结构导引律为：

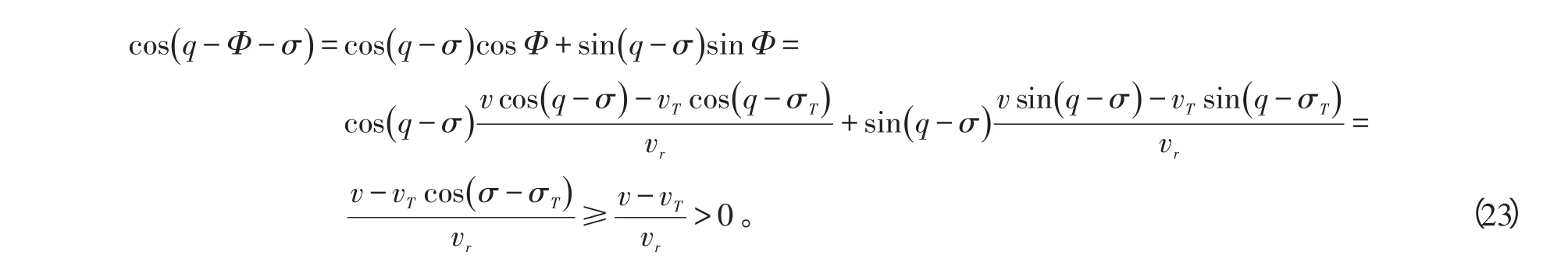
由式（23）得cos(q-Φ-σ)〉0，综合式（22）、（23）可知系统控制量总是非奇异的。表明将相对航向误差角作为控制目标，可不受导弹初始弹道角的限制。

3 仿真研究

仿真研究在反舰导弹导引头试验数据动态处理仿真软件上进行，以低弹道侧向弹道仿真为例，仿真条件为导弹初始高度200 m，弹目初距5 km，导弹速度500 m/s，设定末端落角为-15°，导弹初始航向角150°，目标运动采用实际反舰导弹打靶试验数据。

图2～5为带落角约束的变结构导引律作用下的仿真曲线，其参数设置为K=0.2、k1=0.1、c2=0.04、c3=0.05。

图2 变结构导引律下弹目相对运动轨迹Fig.2 Relative motion trajectory of m issile and target under variable structure guidance law

图3 变结构导引律下S仿真曲线Fig.3 Simulation curve of Sunder variable structure guidance law

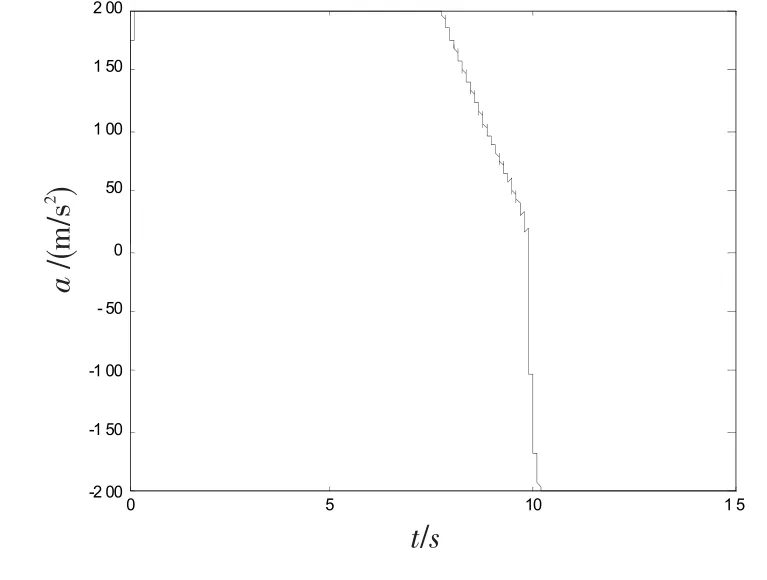
图4 变结构导引律下加速度仿真曲线Fig.4 Simulation curve of aunder variable structure guidance law

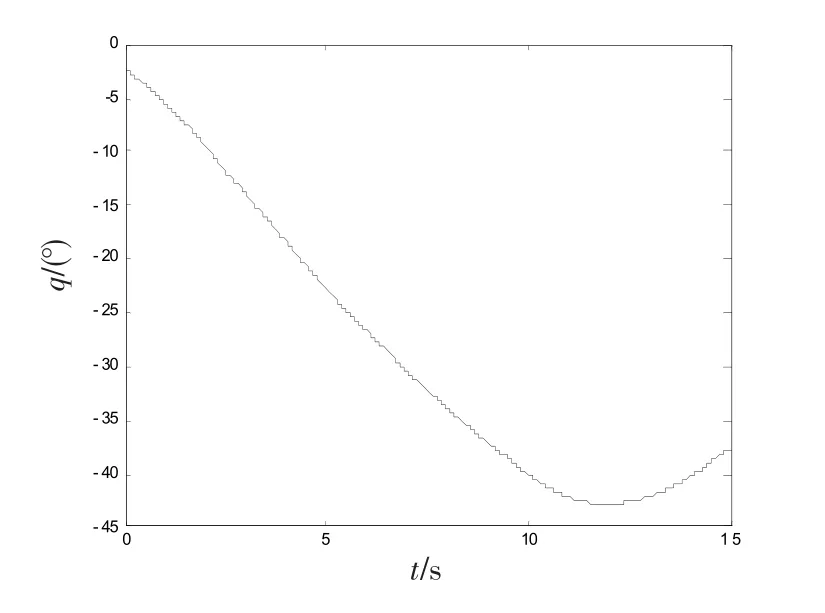
图5 变结构导引律下q仿真曲线Fig.5 Simulation curve of qunder variable structure guidance law

图6～9为带落角约束的非奇异变结构导引律作用下的仿真曲线，参数K=1、k1=0.01、c3=1、c5=3。

从仿真结果可知，当导弹初始航向角为150°，设定末端落角为-15°时，采用带落角约束的变结构导引律，脱靶量为9 311 m，落角为-2.29°，导弹脱靶，不能命中目标，落角也不能满足要求；采用带落角约束的非奇异变结构导引律，脱靶量为0.15 m，落角为-12.2°，导弹命中目标，则能同时满足脱靶量和落角。

图6 非奇异变结构导引律下弹目相对运动轨迹Fig.6 Relative motion trajectory of m issile and target under nonsingular structure guidance law

图7 非奇异变结构导引律下S仿真曲线Fig.7 Simulation curve of Sunder nonsingular structure guidance law

图8 非奇异变结构导引律下加速度仿真曲线Fig.8 Simulation curve of aunder nonsingular structure guidance law

图9 非奇异变结构导引律下q仿真曲线Fig.9 Simulation curve of qunder nonsingular structure guidance law

4 结论

在反舰导弹导引律的设计问题上，以往都采用比例导引律。然而，当存在目标机动时，为了截获目标，比例导引律需要大的加速度命令，这样一来可能导致脱靶。针对上述问题，本文提出了一种反舰导弹滑模非奇异变结构导引律，在基于变结构理论的基础上，推导了具有带落角约束的非奇异变结构导引律，通过仿真研究，验证了导弹能同时满足脱靶量和落角的性能指标要求，并具有精度高、脱靶量小和抗干扰性强的优点。

[1] HA IJ，HUR JS，KO MS.Performance analysis of png laws for random ly maneuvering targets[J].IEEE Transactions on Aerospace and Electronic System，1990，6（5）：713-721.

[2] CHOH，RYOO CK.Closd-rorm optiminal guidance law for missiles of time-varying velocity[J].Journal of Guid-ance，Control，and Dynamic，1996，19（5）：1017-1022.

[3] GERARD L.Guidance algorithms design：a nonlinear inverse aspproach[J].Jouanal of Guidance，Control，and Dynamics，1998，21（5）：742-746.

[4] KIMK B，KIMMJ，KWON W H.Receding hoizon guidance laws with no information on the time-to-go[J].Jouanal of Guidance，Control，and Dynam ics，2000，23（2）：193-199.

[5] KIMB S，LEE JG，HAN HS.Based PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic System，1998，34（1）：277-288.

[6] FENG Y，YU XH，MAN ZH.Non-singular adaptive terminal sliding mode control of rigid manipulators[J].Automatica，2002，38（12）：2159-2167.

[7] CHIOU YC，KUO CY.Geometric approach to three-dimensional missile guidance problem[J].Journal of Guidance and Control，1998，21（2）：335-341.

[8] RYU JH，PARK CS.Plant inversion control of tail-controlled missiles，AIAA-97-3766[R].New York：AIAA，1997：1691-1696.

[9] CHWA DK，CHOI JY.New parametric affine modeling and control for skid-to-turn m issiles[J].IEEE Transactions on Control Systems Technology，2001，9（2）：335-347.

[10] YUAN PJ，CHERN JS.Ideal proportional navigation[J]. Journal of Guidance，Control，and Dynam ics，1992，15（5）：1161-1165.

[11] TYAN F.An unified approach to missile guidance laws：A 3D extension[C]//Proceedings of the American Control Conference.AK，2002：1711-1716.

[12] ALDER F P.Missile guidance by three-dimensional proportional navigation[J].Journal of Applied Physics，1986，27（3）：500-507.

[13] SHINAR J，ROTSZTEIN YBEZNER.Analysis of threedimensional optimal evasion with linearized kinematics [J].Journal of Guidance and Control，1989，2（5）：353-360.

[14] ZHOU D，MUC，XUW.Adaptive sliding-mode guidance of a hom ing missile[J].Journal of Guidance，Control，and Dynam ics，1999，22（4）：589-594.

Design and Simulation of Anti-Ship Missiles Guidance Law Based on the Non-Singular Sliding Mode

ZHOU Yuana,LEI Jun-weib,XUE Yu-tingb
（Naval Aeronautical and Astronautical University a.No.7 Department; b.Department of Control Engineering,Yantai Shandong 264001,China）

A kind of anti-ship missiles guidance law based on the non-singular sliding mode was proposed in this paper. Based on the kinematics analysis method of anti-ship ballistic missile,the mathematics model of missile target relative motion was established.On the basis of the non-singular theory,guidance law based on the non-singular sliding mode which had the angle constraint was deduced.It was showed that the guidance law could meet performance index of missing target and falling angle at the same time by simulation.The guidance law had excellent robustness.The distance of missing target was smaller,the precision was higher.Compared with the traditional proportional guidance law,it had stronger practicability and effectiveness.

anti-ship missiles;guidance law;sliding mode;non-singular;robustness

TJ765.2+2

A

1673-1522（2014）04-0301-05

10.7682/j.issn.1673-1522.2014.04.001

2014-03-27；

2014-05-05

国家自然科学基金资助项目（51005242）

周源（1979-），男，讲师，博士生。