基于Petri网的登陆作战中协同通信的性能评价*
2014-07-11于夫
于 夫
(92941部队96分队 葫芦岛 125000)
1 Petri网简介
Petri网的概念最早在1962年Carl Adam Petri的博士论文中提出来。Petri的工作引起了欧美学术界与工业界的注意。1970年~1975年,MIT的计算结构研究小组积极参与Petri网相关的研究。到现在已出版了包括高级网在内的许多Petri网专著[1]。
这里首先引出Petri网的一般概念:
定义1 当一个三元组N=(S,T;F)是一个Petri网if(当且仅当):
1)S∪T≠φ(网非空);
2)S∩T≠φ(二元性);
3)F⊆(S×T)∪(T×S)(流关系仅在S与T的元素之间);
4)dom(F)∪cod(F)=S∪T(没有孤立元素)。
在网中,F的元素叫弧,dom(F)={x|∃y:(x,y)∈F},cod(F)={x|∃y:(y,x)∈F}。
在图形上,S元素用一个圆圈表示,代表位置;T元素用一个四方形或者长方形表示,但常常为了节省空间,仅用一段黑线表示。在X元素之间的流关系由带箭头的弧表示,其方法如下:
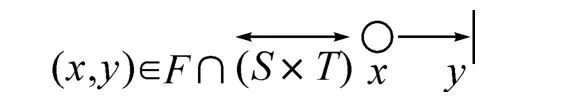
定义2 随机Petri网SPN(stochastic Petri net)
近年来,人们以各种方式把时间引入Petri网,其中常见的有两种引入方式:一是每个位置相关联一个时间参数;二是每个变迁相关联一个时间参数。另外一种在Petri网中引入时间参数的方法是:在每个变迁的可实施与实施之间联系一个随机的延迟时间,这种类型的Petri网叫做随机Petri网。
给Petri网的每个变迁相关联一个实施速率(firing rate),得到的模型就是SPN[2]。
在连续时间随机Petri网中,一个变迁从可实施到实施需要延时,即从一个变迁t变成可实施的时刻到它实施时刻之间被看成是一个连续随机变量xi(取正实数值),且服从于一个分布函数:

在不同类型的连续时间随机网中,这个分布函数的定义是不一样的。当相关于每个变迁的分布函数定义成一个指数分布函数:

其中实参数λt>0是变迁t的平均实施速率,变量x≥0。可证明:
1)两个变迁在同一时刻实施的概率为零;
2)SPN的可达图同构于一个齐次 MC,因而可用马尔可夫随过程求解。
指数分布是满足马尔可夫特性的连续随机变量的惟一分布函数。因此,要想把马尔可夫随机过程应用于SPN的可达图,每个变迁的延时服从于指数分布是充要条件。
2 运用SPN分析登陆作战中协同通信系统性能的可能性
对于登陆作战而言,参加作战的陆、海、空三军及二炮部队均需得到各方的协同;又因登陆作战中敌防御前沿支撑点多,高技术兵器多,可以认为:在登陆作战中,各军兵种必然和多个方向建立协同通信,并且协同通信呼叫率是相当大的[3]。而对有大量用户所形成的呼叫流来说,它们所形成的呼叫流可以看成是一个无后效流,一般大数量的独立信源的来话呼叫可认为是一种泊松呼叫流,即在时间长度t内,恰好发生k次呼叫的概率服从泊松分布:

式中λ为平均到达率,即随机变量的数学期望。
由上式不难求出在t秒内k次或大于k次呼叫的概率:
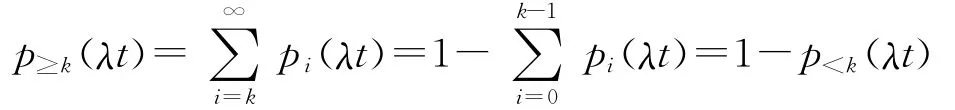
因此,在t时间内没有发生呼叫(k=0)的概率为p0(λt)=e-λt。因此,不难求出呼叫之间的时间间隔的概率分布F(t)。按照随机变量分布函数的定义,F(t)等于呼叫间隔η小于给定值t的概率,即在时间长度t内发生一个或一个以上呼叫的概率,所以有:
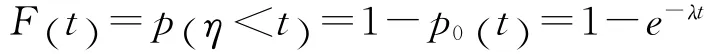
可见,在泊松流情况下,呼叫时间间隔的分布为指数分布。因此,协同通信系统的呼叫流服从指数分布,可以用马尔可夫链等效SPN可达图来分析系统性能[4]。
3 SPN建模分析
SPN应用在系统模型的性能分析中分为三步:
1)给出系统的一个SPN模型;
2)构造出该SPN所同构的MC;
3)基于MC的稳定状态概率进行所要求的系统性能分析。
下面用SPN理论来分析登陆作战中集团军利用协同通信分队组成此网的时延情况。
集团军内各作战群在作战过程中的协同通信决策过程如图1所示。
根据以上分析,建立如图2所示的Petri网:
图中○表示位置,用P表示,|代表事件发生的条件,→表示变迁,用t表示,代表事件的发生。

图2 基于Petri网的协同通信决策流程图
图中共有11个位置和14个变迁,为了表示协同通信动作的重复性,在变迁t13和位置P1,变迁t14和位置P1之间通过有向弧进行连接,分别表示各兵种间协同和军种间协同。变迁的实施速率λ表示在可实施的情况下单位时间内平均实施次数,在各次变迁中是不同的,根据作战实际情况,其平均实施速率集为λ=(11111111212111)在初始位置P1有标识,如图示(即有敌情需协同作战),初始状态M1=(10000000000),由M1出发经不同的变迁可得如下Petri网状态:

等效于如图3所示马尔可夫链。
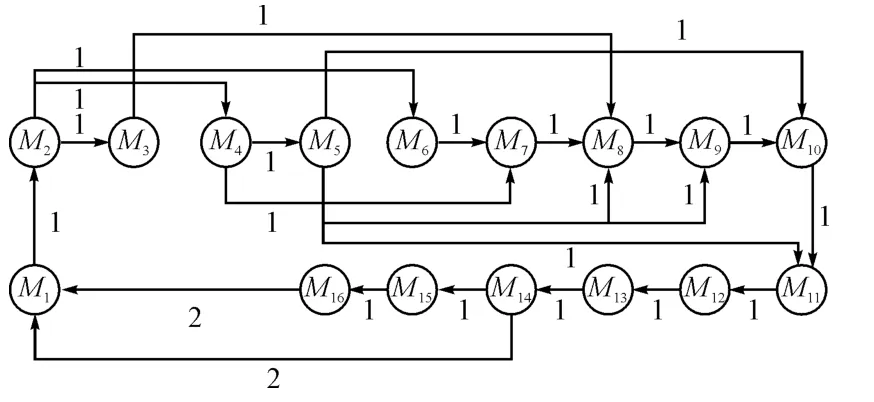
图3 马尔可夫链
根据以上所得,可以列n+1个齐次方程,含有n(n=16)个未知变量,加上∑ixi=1,即可求出每个可达标识的稳定概率:



由稳定状态下流量关系的Little公式¯N=¯λ¯T,¯T为t1的平均发射时间,它是平均发射率的倒数,即¯T=1/λ=1,¯λ表示通过t1的平均流量,于是¯λ=0.1076。我们可以利用Little规则和平衡原理,计算非零回归的MC,子系统的流入流出速率应该平衡(相等)。根据Petri网性质,t1一旦发射,它将向P2、P3、P4各输出一个标识,故t1-t14之间的总流量是=3=0.3228。
子系统的平均延时时间为
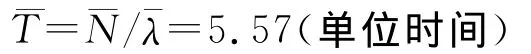
在作战忙时(抢滩上陆和建立登陆场),由于各种障碍物及火力点众多,加之敌强调先制与反制作战,敌必然将各类兵力、兵器靠前配置并大量集中使用于此阶段,战役任务将极为艰巨,作战协同任务繁重,一梯队集团军内各单位呼叫协同及集团军向各军种呼叫协同率合计约为200次/小时,即λ=3.33(次/分钟),平均每次呼叫间隔18s,各协同通信分队发出协同通信信息需要的时间为2个单位时间,整个协同通信系统的期望时延为18×2×5.75=207s=3.45min。
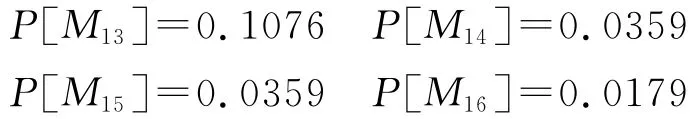
在稳定状态下,每个位置中所包含的标记数量的概率,对∀s∈S,∀i∈N,令P[M(s)=i]表示位置s中包含i个标记的概率,即可从标识的稳定概率求得位置s的标记概率密度函数如下
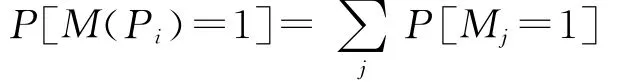
其中Mj∈[M0],且Mj(s)=i。

由此可求出子系统位置集所含的平均标记数:
4 结语
由上文SPN分析可知,登陆作战中集团军内部组织协同通信网,协同动作的延时时间约为3.45min,比传统的作战协同通信具有更高的效率,能够更有效地保证大型岛屿联合进攻作战的协同。本文对登陆作战中协同通信研究有一定借鉴意义。
[1]林闯.随机Petri网和系统性能评价[M].北京:清华大学出版社,2000:302-311.
[2]高东华.登陆作战中电子对抗战术运用[C]//赵利德主编.98烟台学术研讨会论文集.北京:中国人民解放军射击学会,1998:96-99.
[3]魏碧海.海南岛战役渡海登陆作战的历史经验与思考[J].军事历史,2001:33-35.
[4]王作超.集团军登岛作战通信需求分析系统研究报告[J].重庆:通信指挥学院,2000:100-105.
[5]唐春生.现代登陆战役电子战法研究[J].海军学术研究,1995,1:82-83.
[6]王新建.信息化条件下登陆作战探析[J].国防大学学报,2007,1:30-32.
[7]高东华.舰艇电子对抗作战指挥[M].北京:海潮出版社,2002,4:100-102.
[8]齐德学.中外登陆作战经验教训[M].北京:军事科学出版社,2006:24-26.
