三级同步感应线圈炮的模型及控制研究
2014-07-10陈学慧孟昭福邹本贵王旻
陈学慧,孟昭福,邹本贵,王旻
(1. 海军航空工程学院, 山东 烟台 264001; 2. 装甲兵工程学院,北京 100072)
0 引言
电磁炮按照结构和原理不同可分为轨道炮、线圈炮、重接炮3种[1-2]。同步感应线圈炮(synchronous induction coilgun, SICG)是线圈炮的一种,它具有弹丸与驱动线圈无机械接触的特点,并可以通过增加驱动线圈的级数来提高弹丸的速度,适合发射大质量的弹丸[3-5]。所谓同步,是指利用驱动线圈的单级电流脉冲进行触发,有别于利用多级电流脉冲触发的异步感应线圈炮;所谓感应,是指线圈炮中电枢的电流由互感产生,有别于由导轨或电刷直接导入电流的螺旋线圈炮[6-8]。多级同步感应线圈炮是高功率电磁发射器,其模型十分复杂。由于其级数的增加,控制策略和控制方法显得更为重要。为了准确分析其发射过程,本文使用数值仿真方法对一个三级同步感应线圈炮的发射过程进行研究,并用时间控制策略进行了实验。
时间控制和空间控制是2种不同的控制策略。目前对多级同步感应线圈炮触发控制系统的设计研制普遍采用位置检测触发控制和延时触发控制这2种方法。位置检测触发控制由于各级控制独立,相互影响小,一般应用于级数较多的场合,如美国于2004年使用466级驱动线圈将质量为20 kg的弹丸加速到2 500 m/s[9]。但位置检测触发控制系统存在2个较大的缺陷:一是位置检测传感器一旦装好,电枢的触发位置就确定了,因此这种控制方式缺少灵活性。二是当电枢在高速或者超高速飞行时,位置检测传感器就有可能无法响应。延时触发控制和位置检测触发控制相比具备较好的灵活性,也不存在触发控制系统失效的问题,因此本文采用基于时间控制的方法对同步感应线圈炮进行仿真和实验分析。
1 基本工作原理
三级同步感应电磁线圈发射器由储能电容、同步触发控制电路及开关、驱动线圈和电枢等组成,在发射过程中,先对第1级的驱动线圈馈电,然后其余各级螺旋线圈依次馈电,模型如图1所示。工作原理如下:闭合左边第1级驱动线圈的电路开关,根据电磁感应定律,当驱动线圈通以变化的电流时,在线圈的周围产生的磁场亦是变化的,可知电枢中有感应电流产生,2种电流产生的磁场相互作用,在驱动线圈和电枢之间产生与轴线水平和垂直2个方向的作用力。垂直方向上的电磁力作用效果因为轴对称而相互抵消;水平方向的电磁力的作用效果是在驱动线圈固定时,推动电枢水平向右运动。当电枢越过第2级驱动线圈适当位置后闭合第2级电路开关,给第2级驱动线圈馈以脉冲电流,那么电枢又被感应出和驱动线圈中电流方向相反的电流,电枢又受到向右的排斥力继续被加速。同理,进入后面的驱动线圈,电枢被不断地加速驱动,直至最后飞离发射器。
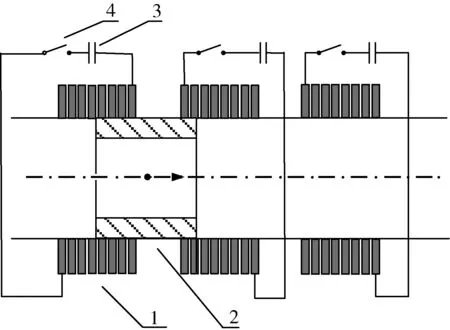
1—驱动线圈;2—电枢;3—电容器;4—开关图1 三级电磁线圈炮模型Fig.1 Model of new electromagnetic launcher
2 三级SICG数学模型
本文采用MAXWELL软件对三级SICG进行2D仿真。要得到系统的完整描述,就要建立电磁场数学模型,并求出模型的解。电磁场数学模型的解,需从求解低频电磁场麦克斯韦方程组开始:
▽×H=J,
(1)
▽·B=0,
(2)
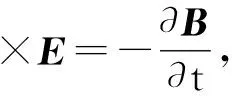
(3)
式中:H为磁场强度;J为电流密度;B为磁通密度;E为电场强度;t为时间。
H=νB,
(4)
式中:ν为磁阻率。
在导体中的欧姆定律为
J=σE,
(5)
式中:σ为电导率。
场路耦合法是解决电磁发射问题的比较好的方法。场路耦合的分析方法根据求解变量采用矢量磁位A还是矢量电位T,可以分为A法和T法两大类[10-12]。A法由于引入耦合电压项方便,且易于处理多连域问题,因此广泛应用于低频电磁场的求解,因此本文采用基于A法的场路耦合分析方法。
选择函数S,使
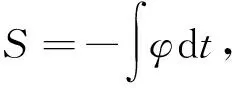
(6)
并设

(7)
(8)
则在库仑规范▽·A′=0下,电磁场控制方程可表示为
(9)
当忽略导体区涡流时,电流密度JS和导体总电流i(t)有如下关系:
(10)
式中:Sc为绕组截面积;Nc为线圈匝数。
写成矩阵形式为
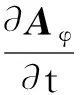
(11)
由于三级电路的开关轮流闭合,各回路没有同时通电,加上驱动线圈之间有一定的间隔,所以不考虑驱动线圈之间的互感问题,系统等效电路模型如图2所示。
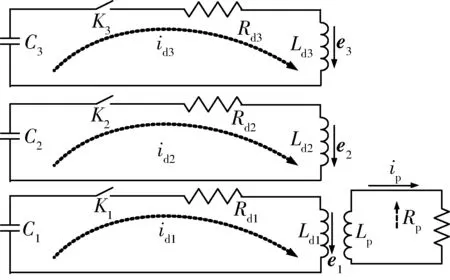
图2 三级电磁发射器驱动电路Fig.2 Driving circuit of the launcher
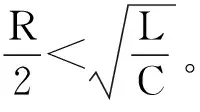
忽略驱动线圈中的涡流,等效电路方程如下所示:
Uci(t)=Rdiidi(t)+ei.
(12)
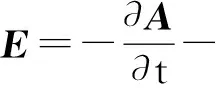
(13)
以上式(12),(13)方程是系统的电路方程,写成矩阵形式为
(14)
将式(11)与式(14)联立,可得三级同步感应线圈炮的场路耦合模型为
(15)
将式(15)进行时间离散,并对离散结果进行处理,便可对场路耦合模型进行求解。再结合推力方程(16)和运动方程(17),对其进行联合求解便可求出驱动线圈和电枢中的电流、弹丸受力、弹丸速度和弹丸位移等物理量[10]。
(16)

(17)
式中:Ndi为第i个驱动线圈的匝数;Np为电枢的匝数;Mdip为第i个驱动线圈和电枢的互感;Idi为第i个回路的电流;m,v,z分别为电枢的质量、速度和位移。
3 三级SICG仿真
3.1 物理模型参数及仿真初始条件
在MAXWELL软件中建立三级SICG的结构模型和电路模型如图3所示。设置驱动线圈材料为铜,电枢材料为铝,运动区域和包裹层均为空气。驱动线圈高9 cm,厚1 cm,匝数为200匝,驱动线圈之间间隔9 cm。电枢高13 cm,宽1.5 cm,电枢初始位置为6.5 cm(第1级驱动线圈和电枢的中心距)。仿真时运动区域宽2.65 cm,高240 cm,周围包裹的空气宽1.5 cm,高15 cm。使用最大长度限制来划分网格。电容器C的初始电压0.4 kV,容量1 000 μF,R均为0.5 Ω。弹丸质量设为650 g。电枢的初始速度设为0,仿真起始时间为0,终止时刻为200 ms,时间步长取0.5 ms。延时设置采用电流源串联电流控制开关的从电路来获得,第2级延时时间为50 ms,第3级延时时间为70 ms。
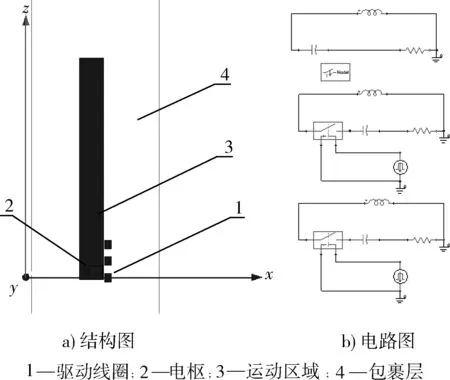
图3 三级同步感应线圈炮结构和电路图Fig.3 Structural and circuit diagram of three-stage SICG
3.2 仿真结果及分析
图4给出了各级驱动线圈电流的波形。从图中可以看出,驱动线圈电流波形是一种典型的欠阻尼RLC串联电路电流波形,呈近似衰减状的正弦分布,各级延时时间也可以从图中清楚地看出。
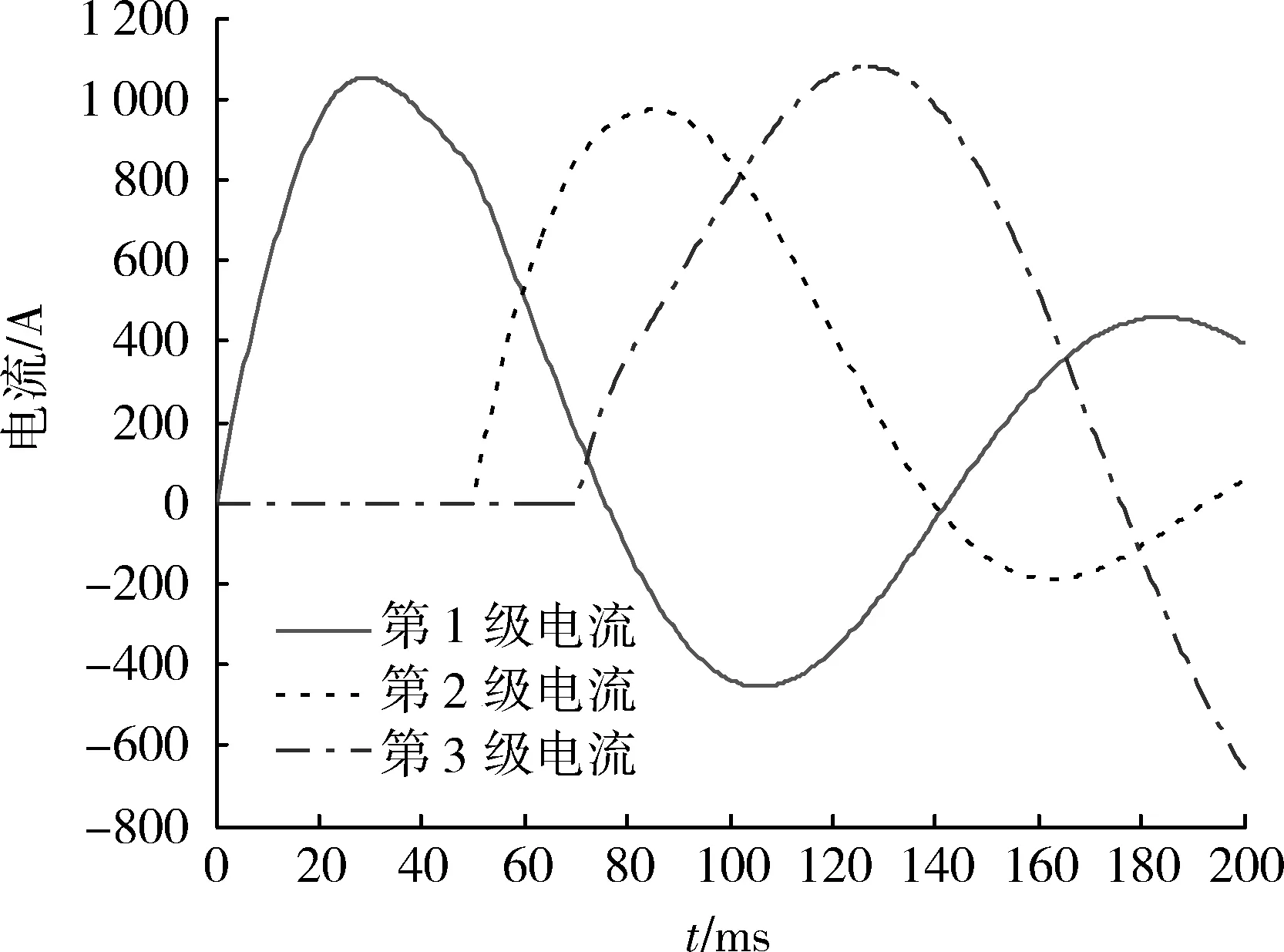
图4 各级驱动线圈电流波形Fig.4 Current′s wave of each drive coil
电枢受力和速度的波形如图5所示。从图中可以看出电枢有3个受力峰值,在27.5 ms时第1级驱动线圈对电枢的作用力峰值达到149.4 kN,61 ms时第2级驱动线圈的作用力峰值达到89.1 kN,78 ms时第3级驱动线圈的作用力峰值达到100 kN。电枢的速度在第1级驱动线圈的作用下上升很快,也可以说第1级驱动线圈对电枢速度的提高最为显著。这主要是因为每级电枢动能的增加量与每级出口速度与初始速度的平方成正比:
(18)
式中:ΔE为电枢的动能的增量;v为出口速度;v0为初始速度。
每级驱动能量相同,即使各级效率一样高,速度的增加也只会越来越慢。到120ms以后电枢基本摆脱了各级驱动线圈的作用,速度稳定在13.4m/s左右。

图5 电枢受力和速度波形Fig.5 Waves of force and speed of armature
3.3 三级SICG实验
为了验证仿真结果的正确性,搭建了一套实验装置。实验装置采用基于仿真的延时触发控制方式。根据仿真得到的各级驱动线圈的最佳触发时刻,通过设定触发时间的方式实现各级线圈的触发。由仿真计算出延时触发序列之后,通过串口助手将启动命令和延时控制参数通过串口传给单片机,单片机按顺序发出电平信号触发各放电回路触发开关,从而控制各级电容器组向线圈放电,线圈推动电枢飞出发射管。
触发控制装置包括:上位机(PC),单片机触发控制电路,触发开关。作为定时器和信号发生器的单片机触发控制电路是触发控制系统的核心。控制信号流程和系统硬件的总框架如图6和图7所示。

图6 触发控制信号流程Fig.6 Flow of trigger signal
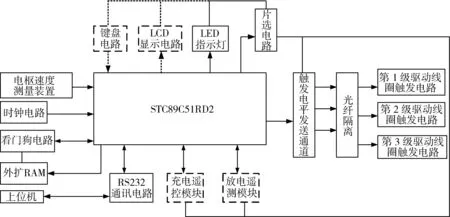
图7 系统硬件总体框架Fig.7 Structure of the system
关键的控制参数是电枢从初始位置到达第2级驱动线圈和第3级驱动线圈最佳初始位置的运行时间。通过仿真,求出电枢从第1级初始位置运动到第2级最佳初始位置的运动时间和位移,得到电枢的运行时间T1,也就是第2级驱动线圈的控制参数。同理,可以通过仿真计算出,电枢从第2级驱动线圈的最佳初始位置运动到第3级最佳初始位置,就得到了电枢从第2级驱动线圈最佳初始位置到第3级驱动线圈最佳初始位置的运动时间T′,T2=T1+T′就是第2级驱动线圈的控制参数。
本文的实验研究采用了三电极放电间隙开关,如图8所示。该开关可以实现TTL电平触发。按照三级SICG物理仿真模型的结构参数制作驱动线圈和电枢的实物模型并进行实验。实验测得了回路电流和电枢的速度。回路电流的测量采用Rogowski线圈法,由示波器测得Rogowski线圈的感应电压波形,再按照一定的比例关系换算成驱动线圈电流。电枢速度的测量采用网靶测速法,电枢通过测速区域时撞断2个网靶的铜丝,由示波器采集延时时间,两网靶的距离除以延时时间便是电枢的速度。得到的仿真结果与实验结果对比如表1所示。

图8 三电极间隙开关原理图及实物Fig.8 Principle diagram and object of gap switch with three electrodes
表1 仿真和实验结果对比Table 1 Contrast of results between simulation and experiment

参数炮口初速/(m·s-1)第1级驱动电路最大电流/A第2级驱动电路最大电流/A第3级驱动电路最大电流/A仿真13.41 0539731 080实验12.01 1009501 010
从表中可以看出,炮口初速的仿真结果比实验结果大12%,驱动电流的最大电流差别在10%以内,证明仿真结果真实有效。
4 结束语
本文利用有限元方法建立了三级同步感应线圈炮物理模型。给定系统参数,对场路耦合下驱动线圈的电流分布和电枢的运动特性进行了仿真分析,并搭建了实验装置进行了物理实验。仿真和实验结果表明,通过延时放电的方式能实现对三级同步感应线圈炮的同步控制。
参考文献:
[1] AUBUCHON M S, LOCKNER T R, KAYE R J, et al. Study of Coilgun Performance and Comments on Powered Armatures[J]. IEEE Transactions on Magnetics, 2004, 40(1): 141-144.
[2] 王莹,肖峰.电炮原理[M].北京:国防工业出版社,1995:96-97.
WANG Ying, XIAO Feng. Principle of the Electric Gun[M]. Beijing: National Defence Industry Press, 1995:96-97.
[3] BUSHWAY R R. Electromagnetic Aircraft Launch System Development Consideration[J]. IEEE Trans. on Magn., 2001, 37(1): 52-54.
[4] KAYE R J, MANN G A. Reliability Data to Improve High Magnetic Field Coil Design for High Velocity Coilguns[R]. Albuquerque, New Mexico: Sandia National Laboratories, 2003.
[5] AUBUCHON M S,LOCKNER T R, KAYE R J, et al. Study of Coilgun Performance and Comments on Powered Armatures[J]. IEEE Trans. on Magn., 2004, 40(1): 141-144.
[6] BALIKCI A,ZABAR Z. BIRENBAUM L. Improved Energy Utilization of Linear Induction Launchers by Considering Each Section as an Individual Sub-Launcher [C]∥Proceedings of 14thSymposium on Electromagnetic Launch Technology, 2008.
[7] 刘元恒,刘少克,魏登武.一种三相异步感应型线圈电磁发射器的研究[J].自动化技术与应用,2006,26(2):82-84.
LIU Yuan-heng, LIU Shao-ke, WEI Deng-wu. Study of a Three Phase Asynchronous Induction Coil Launcher[J]. Techniques of automation & applications, 2006, 26(2): 82-84.
[8] 杨栋,刘振祥,杨丽佳,等.一种螺旋线圈电磁发射器弹丸受力的仿真研究[J].微特电机,2010,38(4):17-19.
YANG Dong, LIU Zhen-xiang, YANG Li-Jia, et al. Simulation Analysis of Forces on Armature in Helical Coil Electromagnetic Launchers[J]. Small & special Electrical Machines ,2010,38(4):17-19.
[9] FAIR H D. Electromagnetic Launch Science and Technology in the United States Enters a New Era[C]∥12th Electromagnetic Launch Symposium, 2004.
[10] TSUKETMAN I A, KONRAD A, MEUNJIER G, et al. Coupled Field-Circuit Problems: Trends and Accomplishments[J]. IEEE Trans. on Magn., 1993, 29(2):1701-1704.
[11] 梁振光,唐任远.大型变压器三维瞬态涡流场场路耦合模型[J].电工技术学报,2003,18(3):17-22.
LIANG Zhen-guang, TANG Ren-yuan. Coupled Field-Circuit Model of 3D Transient Eddy Current Field for Large Transformers[J]. Tranactions of China EelectroTtechnical Society, 2003, 18(3): 17-22.
[12] 梁振光,唐任远.采用场路耦合的三维有限元法分析变压器突发短路过程[J].中国电机工程学报,2003,23(3):137-140.
LIANG Zhen-guang, TANG Ren-yuan. Fault Simulation of Power Transformers Using 3D Finite Element Model Coupled to Electric Circuit Equations[J]. Proceedings of the CSEE, 2003, 23(3): 137-140.
