基于排队论的防空导弹武器系统作战效能研究*

赵广彤，俞一鸣，刘群，王成

(1.北京特种机电技术研究所，北京 100012； 2.北京电子工程总体研究所，北京 100854)

0 引言

防空导弹系统在担任掩护某固定目标或移动目标的任务时,指挥员需要根据被掩护目标的特点,来袭目标特性、种类、目标来袭强度,以及出现的各种空情环境等信息来确定部署防空导弹武器系统的类型及数量,或评估已部署地空导弹的作战效能及效费比。如果部署的导弹数量过多,就会出现资源浪费的现象,过少则不能完成指定作战任务,所以需要一种有效的方法来解决此类问题。从排队论的角度看,防空导弹系统是一个随机服务系统,用排队论方法可以解决这类问题[1-3]。

1 效能分析方法

武器系统效能分析方法多种多样，归纳起来可以分为4类：解析法、指数法、统计法和作战仿真方法。排队论属于统计法中常用的一种分析方法。

1.1 解析法

解析法是根据所描述效能指标与给定条件(常常是低层次系统的效能指标及作战条件)之间的函数关系建立解析表达方式并计算获得武器系统作战效能。解析表达式可以直接根据军事运筹理论建立，也可以用数学方法求解所建立的效能方程得到。早在第一次世界大战初期，英国人Lanchester F W建立了描述作战双方兵力损耗过程的微分方程——Lanchester方程，开创了用数学理论研究作战效能的先河。另外，ADC法、排队论法等都属于此类方法。解析法的特点是表达公式明了，易于理解，计算简单，且物理意义明确、便于进行变量间关系的分析和应用。但所能考虑的因素少、只在严格限定的假设条件下有效，否则难于求解，因此只适宜于简单问题的描述或低层次问题的表达。

1.2 指数法

指数法也是一种解析法，由于它突出的特点而成为一种独立的方法。指数法有很多种，如幂指数法、杜佩指数法、综合指数法等。指数法就是把系统中的因素量化为可以对比的相对于同一个量的数值。指数法提出了一个建立在军事专家们的丰富经验之上的统一度量标准，在量化方面有所发展，具有结构简单、使用方便的特点，适用于对武器系统的宏观分析和快速估计，而且指数法的效能模型建立在武器系统自身战技指标的基础上，避开了大量不确定因素的影响，从而增强了评估的确切性，对一些系数的确定也采用了层次分析法等专家评估法。但是，指数法的缺点是描述不细微较粗糙，只适用于宏观评估。

1.3 作战仿真法

作战仿真实质是以计算机仿真模型为试验手段，通过在给定数值条件下运用模型来进行作战仿真试验，由试验得到的关于作战进程和结果的数据可直接或者经过统计处理后给出效能指标的估值。

作战仿真方法考虑了攻防对抗，以具体作战环境和一定兵力编制为背景，能够实施战斗过程的演示，比较形象，但需要大量可靠的基础数据和原始资料作为依托。要得到可靠结果依赖于有计划的、长期大量数据的积累，仿真时对作战环境的模拟比较困难，如干扰环境的不确定性将直接影响结果。总之，作战仿真对于武器系统作战效能分析具有不可替代的作用，能详细地考虑影响实际作战过程的因素，能在一定程度上反映对抗条件和交战对象，考虑了武器系统的协同作用、武器系统的作战过程以及不同规模作战效能的差别，因而特别适合于进行武器系统作战方案的作战效能指标的预测评估。但是，作战仿真方法也存在缺点，一方面建模难度大、编程任务重、仿真试验工作量大，另一方面所得的仿真结果物理意义不明确，并且不易得到规律性结论。

1.4 统计法

统计法是根据实战、演习、试验获得的大量数据，采用数理统计方法对数据进行处理得到一个武器系统的作战效能评估结果。统计法应用的前提是所获统计数据的随机特性可以清楚地用模型表示，由于它直接来源于实践和实战，因此它是最可信、最可靠的效能评估方法。但一个评估方法要有一定的置信度，就必须建立在大量数据的基础上，如果这些数据的取得仅依赖于实践和实战，代价将极其昂贵。因此，它仅适用于武器系统单个效能指标的评估，也很难获得所有因素对效能的影响规律，并且此方法只能用于经过实战的武器系统的效能分析，而不能用于正在设计中的武器系统的效能分析。

排队论是一种常用的统计分析方法，其基本思想是1910年丹麦电话工程师的A.K.埃尔朗在解决自动电话设计问题时开始形成的，当时称为话务理论。排队论就是通过对服务对象到来及服务时间的统计研究,得出这些数量指标 (等待时间、排队长度、忙期长短等)的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优。凡是出现排队现象的地方,一定有“顾客”，又遵守一定服务规则的“服务机构”,存在一定的“排队规则”。这3个条件构成了排队现象的基本要素,说明了排队现象的和排队服务的基本过程[4-6]。

2 计算模型

运用排队论进行分析，首先明确以下条件[5]：

(1) 来袭目标流服从泊松分布，来袭时间间隔服从负指数分布，即

f1(t)=λe-λt，

式中:λ为目标流强度，即平均单位时间内来袭的目标数；1/λ为目标的平均到达间隔时间。

(2) 防空导弹对每个目标的服务时间(包括拦截时间、射击准备时间和拦截间隔时间)服从负指数分布，即

f2(t)=μe-μt，

式中：μ为服务率，即平均单位时间内拦截的目标数；1/μ为防空导弹对每个目标的平均服务时间。

(3) 目标在防空导弹发射区内的停留时间服从负指数分布，即

f3(t)=νe-νt，

式中：ν表示目标的流失率，即平均单位时间内由于等待时间过长而流失的目标数；1/ν为目标的平均等待时间。

(4) 不考虑目标分配，来袭目标按照“先到达先服务”的规则接受服务，有空闲通道即对目标进行拦截，没有空闲通道目标则排队等待。

3 排队论基本模型

排队论模型的系统状态转移图如图1所示[7]。

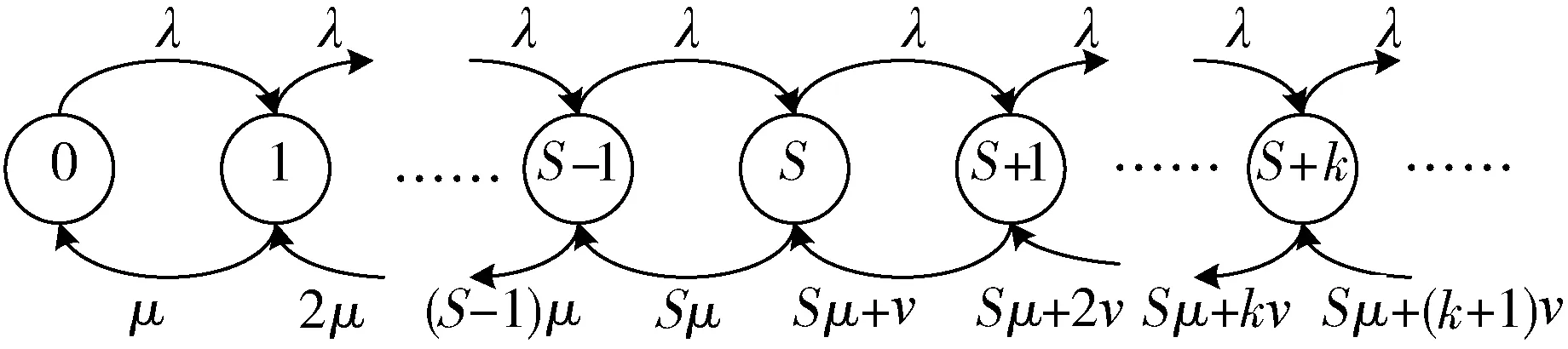
图1 系统状态转移图Fig.1 System state transfer chart

图1中，S为服务台数，即目标通道的数量。

图1表示系统从每一个状态向另一个状态的变化的规律，根据该图可以列出状态转移方程：

式中：Pn(t)为t时刻有n个目标正在接受或等待服务的概率。

当λ>0，μ>0，ν>0的条件下，系统存在稳定解，即当t→+∞时，dPn=0，可以得到稳态概率为[8]

(1)

(2)

(3)

根据little公式可以得到

L=λPt(1/ν)，

(4)

式中：Pt为目标未被拦截的概率；L为队长：

(5)

(5)

将式(5)和式(3)代入式(4)，可以求出：

(6)

因此，目标被拦截的概率为

PA=1-Pt.

(7)

4 事例分析

4.1 蓝方空袭想定

需要的目标参数主要是目标速度、目标来袭强度和目标组成。初步将防空导弹武器系统所拦截的目标分为2类：

(1) 第1类目标

第1类目标为非隐身飞机类目标，对该类目标的拦截受雷达作用距离和导弹可用过载的影响，具有较大反射面积，速度较慢。

(2) 第2类目标

第2类目标为导弹类目标，对该类目标的拦截受雷达作用距离和导弹可用过载的影响，目标的飞行速度较快。

所有目标的平均速度为

(8)

式中：vTi为第i类目标的速度;CTi为第i类目标在总目标中所占比例;N所含目标的种类。

公式(8)用于计算不同类型目标以一定泊松流密度来袭时的平均速度。

4.2 红方武器系统模型

4.2.1 武器系统仿真想定

武器系统仿真想定简单描述如下[9-10]：

(1) 空中目标如果被至少一个雷达站发现，则此空中目标就认为已被观察到；

(2) 发现空中目标时就向火力单元进行目标分配；

(3) 目标分配是按给定的时间步长进行的；

(4) 火力单元各个组成部分的工作按照其功能循环过程进行模拟；

(5) 空中目标只有在被火力单元的雷达发现后，才能从该火力单元发射防空导弹拦截目标；

(6) 对空中目标的射击一直到将其消灭为止，或导弹全部消耗尽为止；

(7) 不考虑火力单元重新装填导弹。

4.2.2 目标分配原则

防空导弹武器系统火力单元的目标分配原则简单描述如下[11-12]：

(1) 只对已发现的空中目标进行目标分配；

(2) 目标只分配给具有空闲火力通道的火力单元；

(3) 对导弹与目标的遭遇点坐标进行预测，并估计此遭遇点是否落入火力单元的杀伤区内；

(4) 目标分配以拦截时间总和为最小原则。

4.3 仿真计算结果分析

俄罗斯“道尔-M1”防空导弹武器系统1个火力单元(1辆战车)即可作为1个作战单元，目标通道数S=2，“响尾蛇”防空导弹武器系统1个火力单元目标通道数S=1，1个作战单元的目标通道数S=3。

以2型武器系统仿真参数作为仿真输入，参见表1。分别对拦截固定翼飞机、导弹类目标以及同时拦截多类型目标时的作战效能进行了计算，分别计算了“道尔-M1”1～4辆战车和“响尾蛇”1个作战单元的作战效能。

表1 杀伤空域参数表Table 1 Velocity and killing zone

(1) 对单一目标的作战效能

拦截相同目标流的固定翼飞机类目标时，“道尔-M1”作战效能较“响尾蛇”具有明显优势。尤其应对大目标流强度时，仍保持较高的作战效能。计算结果见表2，对比情况见图2。

表2 拦截固定翼飞机的作战效能计算结果Table 2 Combat effectiveness contrast results of heading off battle plans

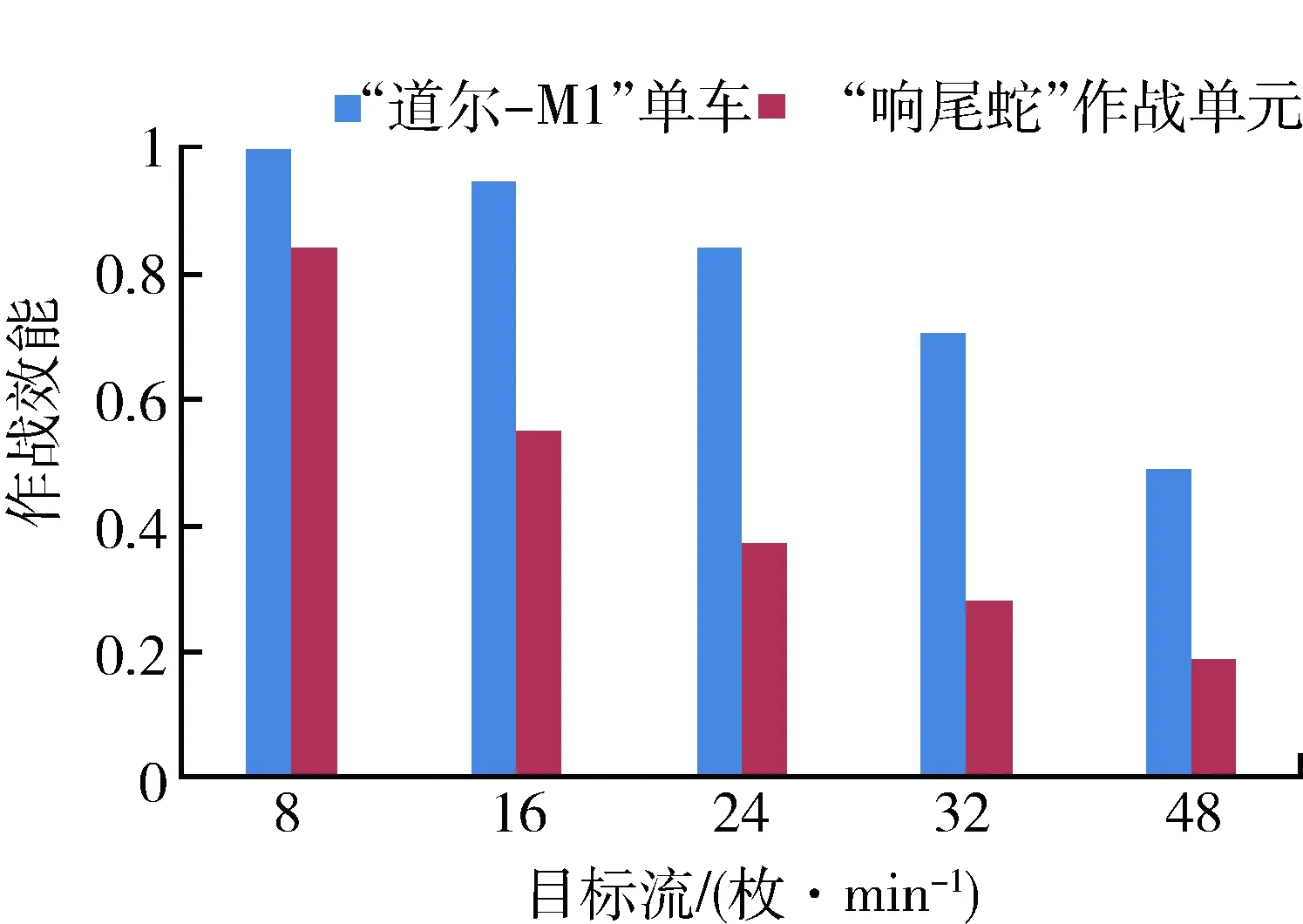
图2 拦截固定翼飞机作战效能对比图Fig.2 Combat effectiveness contrast chart of heading off battle plans

表2中给出了“道尔-M1”1～4辆战车和“响尾蛇”1个作战单元的作战效能。由于“道尔-M1”1辆战车就可作为1个作战单元使用，所以图2给出了“道尔-M1”1辆战车与“响尾蛇”1个作战单元的作战效果对比图。

拦截导弹类目标，在目标流不大情况下，“道尔-M1”与“响尾蛇”均能保持较高的作战效能，当应对大目标流强度时，“道尔-M1”系统仍保持较高的作战效能。详细计算结果见表3，对比情况见图3。

表3 拦截导弹类目标的作战效能计算结果Table 3 Combat effectiveness contrast results of heading off missiles

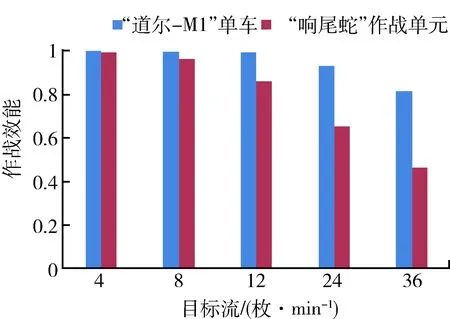
图3 拦截导弹类目标作战效能对比图Fig.3 Combat effectiveness contrast chart of heading off missiles

如表4和图4所示，在相同目标类型、目标数量及目标流强度条件下，“道尔-M1”较“响尾蛇”具有高的作战效能。当目标流为24枚/min时(包括12枚固定翼飞机和12枚巡航导弹)，“道尔-M1”1辆战车仍能保持较高的射击效能(83%左右)，而“响尾蛇”1个作战单元下降较快(37%左右)，已经无法满足有效拦截来袭目标的任务。随着目标流的增大，这种趋势愈发明显，通过增配“道尔-M1”的战车数量，仍能有效拦截来袭目标。

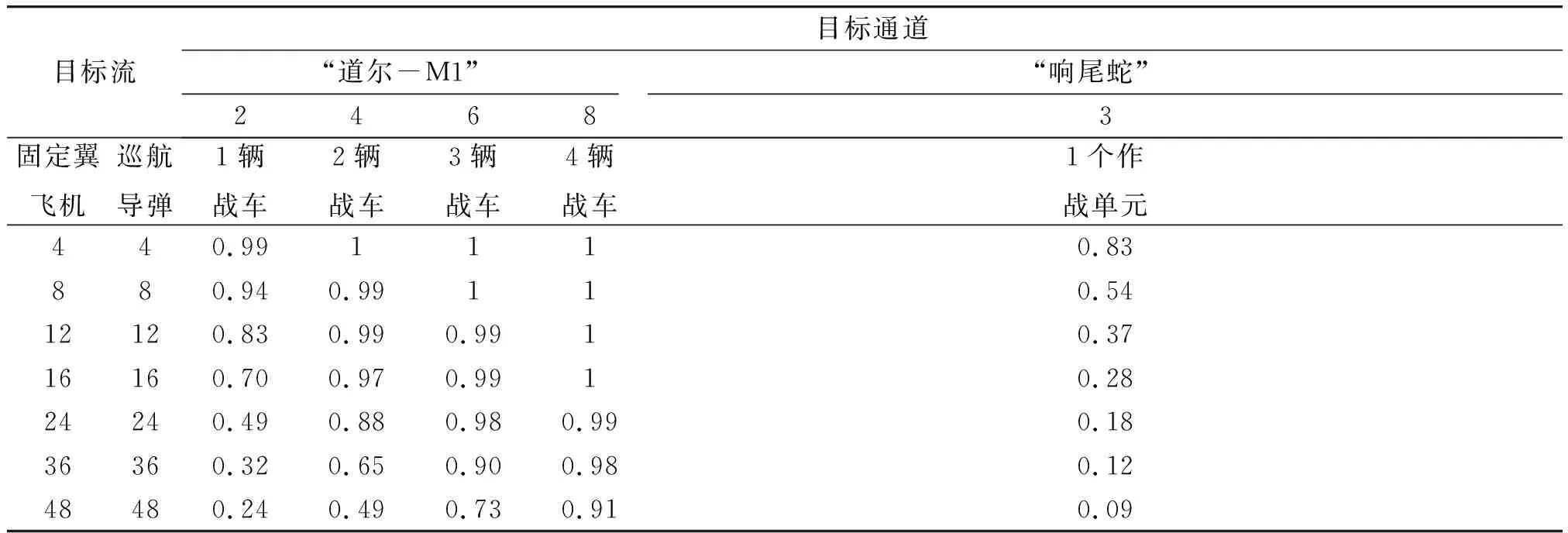
表4 拦截多类型目标的作战效能计算结果Table4 Combat effectiveness contrast results of heading off aims

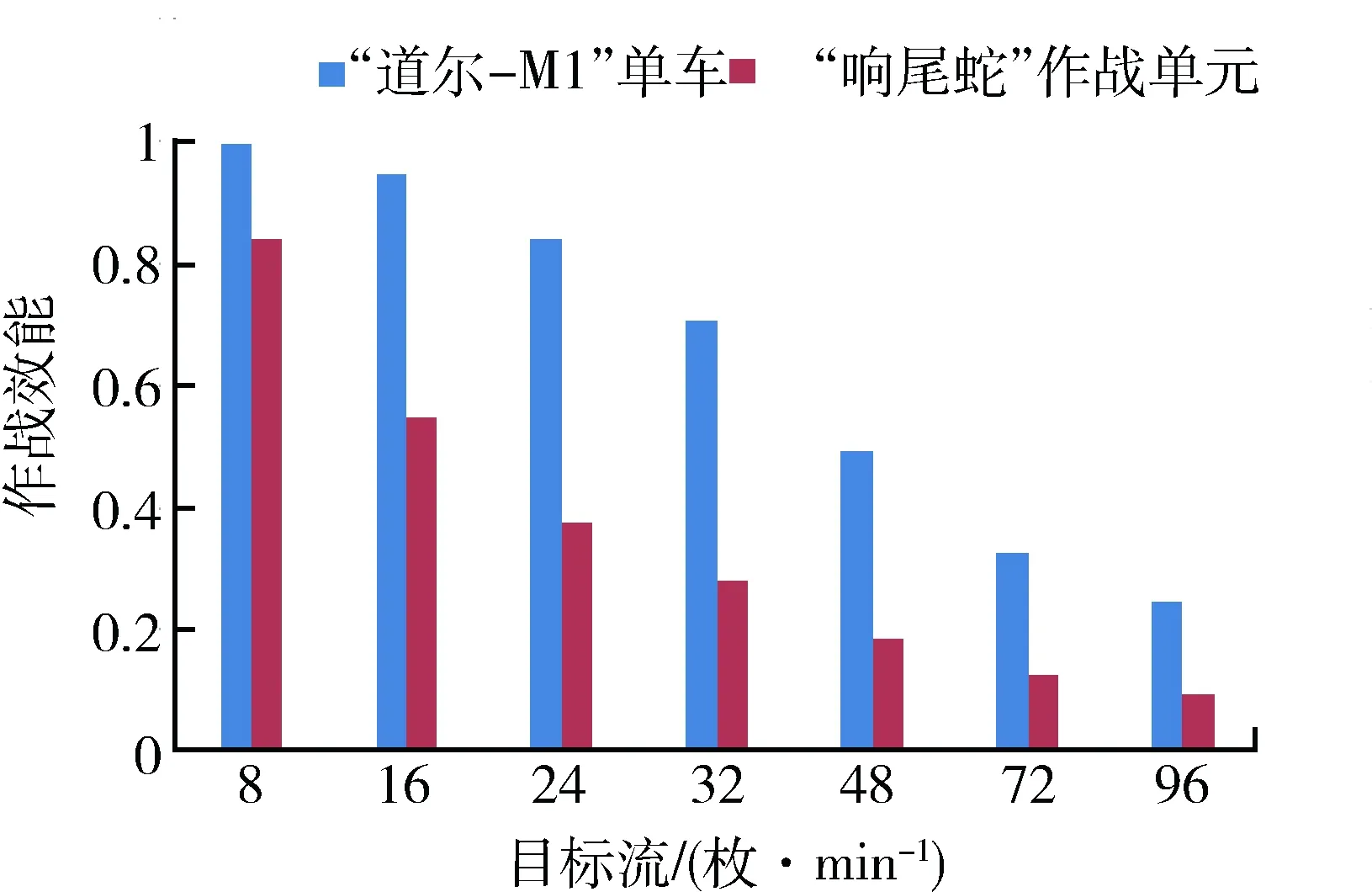
图4 拦截多类型目标作战效能对比图Fig.4 Combat effectiveness contrast chart of heading off aims

5 结束语

本文通过采用排队论的方法，对具有代表性的第2代防空导弹武器系统“响尾蛇”和第3代防空导弹武器系统“道尔-M1”进行作战效能分析。可以看出，第3代防空导弹武器系统由于具备目标通道数多、杀伤空域大及作战部署灵活(1辆战车就可作为独立的作战单元开展作战)等特点，其作战效能远大于第2代防空导弹武器系统的作战效能，尤其针对大批次来袭目标情况下，第3代防空导弹武器系统的作战效能凸显。防空导弹编配部署及作战模式研究可以据此计算结论开展进一步的研究。

参考文献：

[1] 郑春柏，鲁小强，康永文，等. 排队论在地空导弹系统作战评估中的应用研究[J].舰船电子工程，2009(9)：47-49.

ZHENG Chun-bai，LU Xiao-qiang，KANG Yong-wen，et al. Research and Application of Queuing Theory in Surface to Air Missile System Appraisin[J]. Ship Electronic Engineering, 2009(9)：47-49.

[2] 宋志刚，魏太林，朱华邦.基于排队论的舰空导弹系统群的作战效率研究[J].现代防御技术，2008，36(2)：10-13.

SONG Zhi-gang,WEI Tai-lin, ZHU Hua-bang. Queuing Theory Based Evaluation of Ship to Air Missile System Group Operational Effectiveness[J]. Modern Defence Technology, 2008，36(2)：10-13.

[3] 苑立伟,杨建军,张多林. 基于排队论的防空导弹群作战效能研究[J]. 现代防御技术，2005，33(5)：4-7.

YUAN Li-wei, YANG Jian-jun, ZHANG Duo-lin. Research on Operational Efficiency of Air Defencem Issile Group Based on Queuing Theory[J]. Modern Defence Technology, 2005，33(5)：4-7.

[4] 俞坤东,高桂清,赵后随.一种防空系统射击效能的评价模型[J].现代防御技术，2008，36(3)：6-9.

YU Kun-dong, GAO Gui-qing, ZHAO Hou-sui. An Evaluation Model of Fire Efficiency on Air Defense System[J]. Modern Defence Technology,2008，36(3)：6-9.

[5] 罗金亮,王玺.防空导弹网络化作战体系结构及效能评估[J].舰船电子对抗，2010，33(6)：77-80.

LUO Jin-liang,WANG Xi. Structure and Effectiveness Evaluation of Air-Defense Missile Network Combat System[J].Shipboard Electronic Countermeasure, 2010，33(6)：77-80.

[6] 陆传赉.排队论[M].北京：北京邮电大学出版社,2009.

LU Chuan-lai.Queue Theory[M]. Beijing: Beijing University of Post Telecommunication, 2009.

[7] 文仲辉.战术导弹系统分析[M].北京：国防工业出版社,2000.

WEN Zhong-hui.Tactics Missile System Analyse[M].Beijing:Nation Defence Industrial Press,2000.

[8] 刘石泉.弹道导弹突防技术导论[M].北京：中国宇航出版社,2003.

LIU Shi-quan. Ballistic Missile Critical Technology[M].Beijing:China Astronautic Publishing House,2003.

[9] 王正元,刘靖旭,谭跃进,等. 基于作战仿真的装甲车辆作战效能评估方法[J].国防科技大学学报，2004，26(2)：106-109.

WANG Zheng-yuan, LIU Jing-xu, TAN Yue-jin, et al. Combat Effectiveness Evaluation of the Armored Vehicle Based on Combat Simulation[J].Journal of National University of Defense Technology,2004，26(2)：106-109.

[10] 穆中林,于雷,廖俊,等.编队对地攻击作战效能评估指标体系[J].火力与指挥控制,2011,36(1)：87-89.

MU Zhong-lin,YU Lei,LIAO Jun,et al. Research on the Index System of Operational Effectiveness Evaluation for Formation Attacking Ground Target[J].Fire Control & Command Control, 2011,36(1)：87-89.

[11] 彭绍雄，李学园，邹强，等. 基于排队论的舰空导弹武器系统射击效能研究[J].战术导弹技术,2011(4)：5-7.

PENG Shao-xiong，LI Xue-yuan，ZOU Qiang，et al. Research on Antimissile Firing Effectiveness of Ship-to-Air Missile System Based on Queuing Theory [J].Tactial Missile Technology, 2011(4)：5-7.

[12] 张胜涛,娄寿春,王君.基于排队论的防空部署效率分析[J].上海航天，2006(4)：55-57，64.

ZHANG Sheng-tao, LOU Shou-chun, WANG Jun. The Efficiency Evaluation of Air Defense Weapon System Based on Queuing Theory[J].Aerospace Shanghai,2006(4)：55-57，64.