基于最大熵和仿真的导弹装备备件需求预测

赵建忠，徐廷学，李海军，徐衡博

(1．海军航空工程学院 兵器科学与技术系，山东 烟台，264001； 2．中国人民解放军91423部队 装备部，山东 莱阳 265200)

0 引言

备件是导弹装备使用和维修的重要物质基础，其保障水平对于保持导弹装备的战备完好性有着直接的影响。准确地预测备件的消耗数目才能在有限的经费条件下，最大限度地满足导弹装备保障的备件需求。目前，大部分的备件预测方法或模型将备件视为在冷储备条件，即不考虑备件在储备期间发生故障的情况，而事实上导弹装备经常会出现零部件或备件在储备期间损坏而导致短缺的问题，所以它们的预测精度往往不高。因此，建立间断工作导弹装备备件需求预测模型，更准确地确定备件需求量成为亟待解决的问题。

在建立模型之前，首先需要确定导弹装备的寿命分布。导弹装备故障机理十分复杂，而且其备件消耗大都呈现“短周期、小样本”的特点，故采用通过大量数据样本进行建模的方法计算导弹备件的寿命分布参数，效果往往不太理想。实践表明，对于常见统计分布函数，寿命分布假定有时在0.05的水平被拒绝[1]。为了解决这一问题，本文将导弹寿命分布形式看作未知，提出用最大熵法确定寿命分布，并利用遗传算法求解系统建模过程中的非线性规划问题。

文献[2]利用最大熵法来确定统计分布函数参数。由于传统最大熵模型中的约束条件是基于经典矩构建的，因此，基于经典矩的最大熵法能够有效拟合大样本数据的分布函数，然而导弹装备故障的数据往往不能满足大样本条件[3]。本文结合最大熵原理与概率加权矩，提出了基于最大熵原理和概率加权矩的导弹装备寿命分布确定方法。它直接从样本信息出发，不需要对待估随机变量的统计分布类型作任何假定，从而为建立统计分布函数提供了便利。

1 基于最大熵原理与概率加权矩的部件导弹单元寿命分布确定

为了克服基于不同样本量估计的模型对于系统统计特性的描述偏差相差极大的缺陷,本文引入概率加权矩(probability weighted moments, PWMs)方法。根据最大熵原理[4]，对于定义域R上的连续随机变量x(x的概率密度函数为f(x))，假设其累积分布函数F(x)=P(X≤x)及其逆函数x=x(F)存在，则其概率加权矩可以表示为

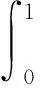
(1)

式中：变量i,n,k为实数。

目前常用的概率加权矩有[5]

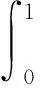
(2)

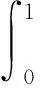
(3)

并设αk与βn对应的无偏估计为ak和bn。

由式(1)可得

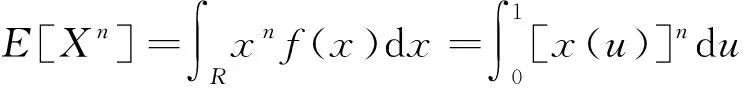
(4)

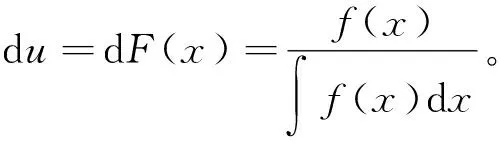
在上述分析的基础上，可得最大熵逆累积分布函数模型

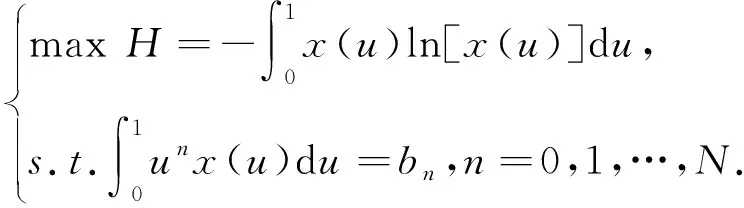
(5)

求解得

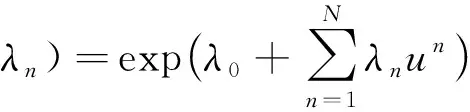
(6)

式中：N为样本矩的最高阶数；λi,i=0,1,…,N为与第i阶矩约束相对应的拉格朗日算子。

如果式(5)中约束等于各阶经典矩，式(6)概率密度函数的约束等于各阶概率加权矩，则式(6)为逆累积分布函数。

在上述分析的基础上，bn可表示为[7-8]

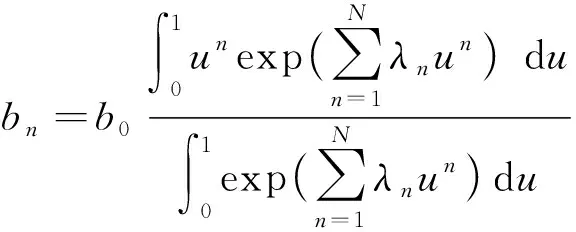
(7)

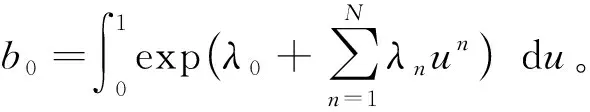
式(7)是关于λi(i=0,1,…,N)的N个方程。

为便于数值求解,将式(7)改写为如下形式：

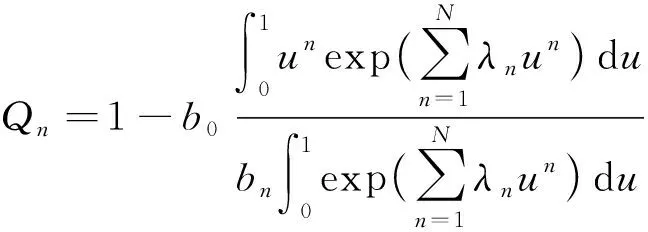
(8)

确定如下优化问题:

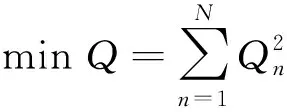
(9)

通过遗传算法求解式(9),可得λi,i=0,1,…,N的值。具体的算法步骤为：①对样本数据进行排序；②计算概率加权矩；③建立残差优化模型，确定优化初始值；④应用遗传算法对模型进行求解；⑤判断是否收敛，若收敛则转⑦，否则转⑥；⑥重新设定初始值，转④；⑦输出计算结果；⑧计算结束。

2 基于保障度的间断工作导弹装备备件需求模型的建立

为建立导弹装备维修备件需求量模型作如下假设：

(1) 某导弹备件供应保障系统由S+1个单元组成。当导弹装备处于工作状态时，认为其中1个单元工作，其余单元作为温储备。当工作单发生故障时，由其中一个没有发生故障的温储备单元替换；如果导弹装备处于停机状态，所有未发生故障的单元均作为温储备。

(2) 初始状态，所有零部件及其备件均为新品，系统中1个零部件在工作，S个备件处于温储备用于替换故障件。

(3) 在每个阶段状态中，系统部件和备件只有正常/故障2种状态，且相同零部件或备件寿命分布相同，零部件在工作期间和备件在储备期间寿命服从同一分布。

(4) 部件只有2种状态：“工作”或“不工作”，即维修保障周期为1年(365天)，装备每周工作tw(h)，其余时间ts=168-tw(h)停机。导弹装备工作时，其零部件处于工作状态，相应的备件处于储备状态。导弹装备停机时，零部件的故障率与备件的故障率相同。

(5) 零部件及其备件均不可修，导弹装备发生故障时进行换件维修，且修复后性能如初，换件时间忽略不计。

(6) 导弹装备如果在工作期间发生故障立即实施维修，如果在停机期间发生故障等到再次开机时实施维修。

(7) 装备系统各组成器件的失效相互独立，其失效不会发生在同一时刻。

(8) 任一器件在发现其不能工作之前总是完好的，即不能工作时间从故障发现时开始。

(9) 装备数量及其所属的零部件数量一定。

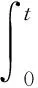
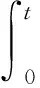
可推导出

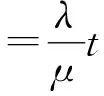
(10)

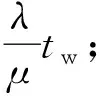
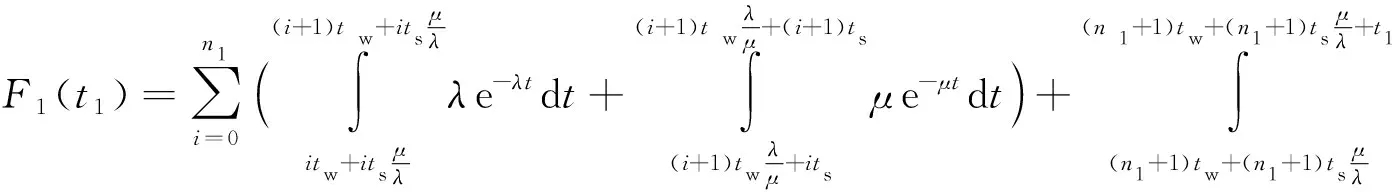
(11)

式中:t1为第1个零部件发生故障前最后一次开机保持良好状态的时间;i表示天数。

则第1个零部件的寿命可表示为

T1=24n1+t1.

(12)

如果处于储备状态的备件没有发生故障，处于工作状态的第1个零部件故障后直接用其替换，则第2个备件的累计故障分布函数可表示为

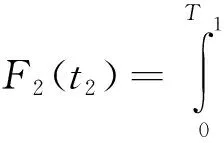
(13)

寿命T2=24(n1+n2)+t2。以此类推，第N个备件的累计故障分布函数为

(14)

通过迭代计算，可以推导出单元的寿命为TN=TN-1-(tw-tN-1)+24n+tN。其中tN为该零部件最后一次开机后良好运行的时间。

这样依次循环直到所以备件都用完，就认为导弹装备不能工作，则最后1个没有在储备期间发生故障的零部件寿命就是备件的可保障时间。

3 仿真思路规划

根据MC直接抽样法[11]，可得到每个单元的累计故障概率抽样值ηj，即[0,1]区间均匀分布的随机数(j=1,2,…,S+1)。由于处于温储备状态的备件也可能发生故障，所以当第1个零部件在工作期间发生故障需要进行换件维修时，首先要判断第2个单元是否已经发生故障。如果没有故障，则立即进行换件维修；否则按以上方法对第3个单元进行判断。以此类推，直到所以备件都用完，就认为导弹装备不能工作。当最后一个零部件的寿命不小于备件供应保障周期时，就认为备件的数量满足需要，否则就是不满足需要。根据Monte-Carlo思想，将上述过程重复Nmn次，记备件满足需要的次数为Nsuc，当Nmn足够大时，Nsuc/Nmn即为备件的保障概率。针对故障概率和平均寿命的计算，进行1 000次仿真运行即可，本文取Nmn=1 000次。

3.1 实例分析

根据调研分析，某型导弹装备及其零部件平时主要处于停机和使用2种状态，即工作和储备2种模式，装备平均每周使用大约12 h，其余时间处于停机储备状态，且装备和备件的储备条件一样。装备发生故障后采用换件维修的方式。对于该型导弹装备某电子模块工作和储备期间的故障情况，这里统计分析了有连续故障记录的20个样本，以该模块的故障间隔时间表示，单位为h，具体如表1所示。要求备件保障度为0.9。

表1 故障统计表

由于该电子模块故障数据较少，适合采用基于概率加权矩的最大熵方法确定寿命分布函数。其中，所用矩的阶数m取为2，具体的m选取参见文献[7-8]。在构造遗传算法时，由于目标函数是求最小值，同时为增大适应度函数间的差距，以提高优秀个体被选中的概率，因此选择目标函数值倒数的1010倍作为遗传算法的适应度函数，求得其参数为：λ0=6.25×10-3，λ1=4.49×10-3，λ2=2.63×10-3，其算法寻优过程如图1所示。经拟合优度检验知，该电子模块工作寿命服从参数为λ=6.25×10-3的指数分布。在此基础上，运用随机生成服从相同参数分布的50组数据样本，分别基于概率密度函数和逆累积分布函数来计算1阶矩，并用在定义域内的积分对于理论总体均值的相对误差来评判不同方法的优劣，具体计算结果如图2所示。图2表明，当样本量少于10时，采用经典矩方法相对误差达到50.033 7%，而采用概率加权矩方法仅为3.969 4%。因此，当样本≤30时，基于经典矩的最大熵方法不太适用；若样本量>30，两种方法均可行，但概率加权矩方法精确度相对高些。同理，可求得储备寿命为服从μ=1.851 8×10-4的指数分布。

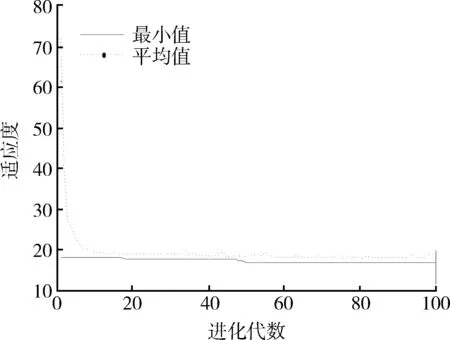
图1 适应度函数图Fig.1 Fitness function figure

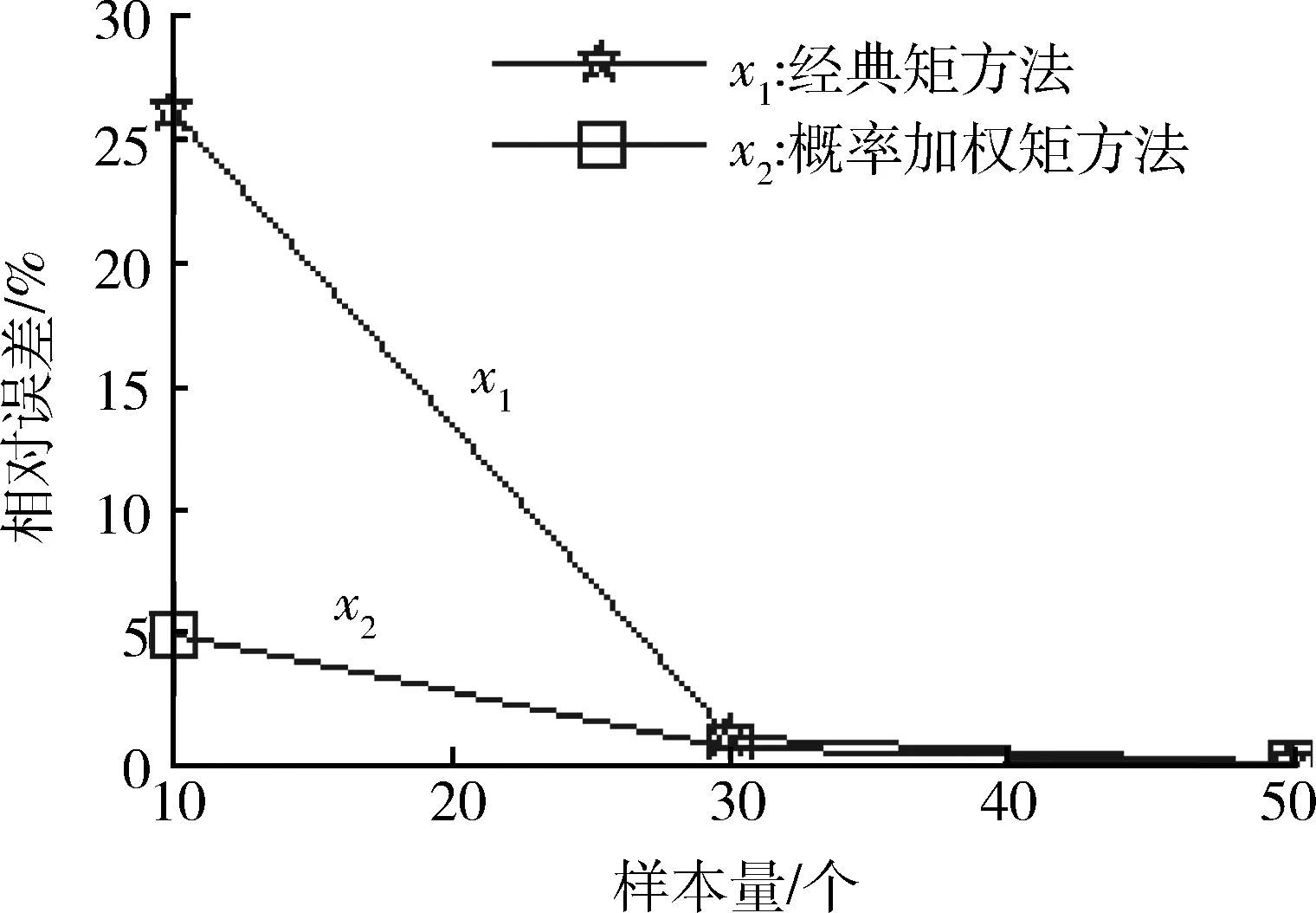
图2 不同样本下2种方法计算相对误差Fig.2 Bias of two different methods obtained from various sample

3.2 需求仿真

利用Matlab编程进行1 000次仿真，该模块1年的备件需求量部分计算结果如表2所示。其中，该导弹装备每周工作20 h时，1年所需备件需求量如图3所示。

3.3 结果分析与评价

表2中，tw=0表示备件一直处于储备状态，可作为温储备看待，即所有单元均以μ=1.851 8×10-4h的故障率进行储备，可利用并联系统公式[12]进行计算，结果为S=1，P=0.928 6。tw=24可视为连续工作的热储备系统，利用热储备系统公式[12]可解得S=6，P=0.928 1。由此可见，2种方法的计算结果是一致的，这说明了本文仿真方法的正确性。

表2 备件需求量计算结果

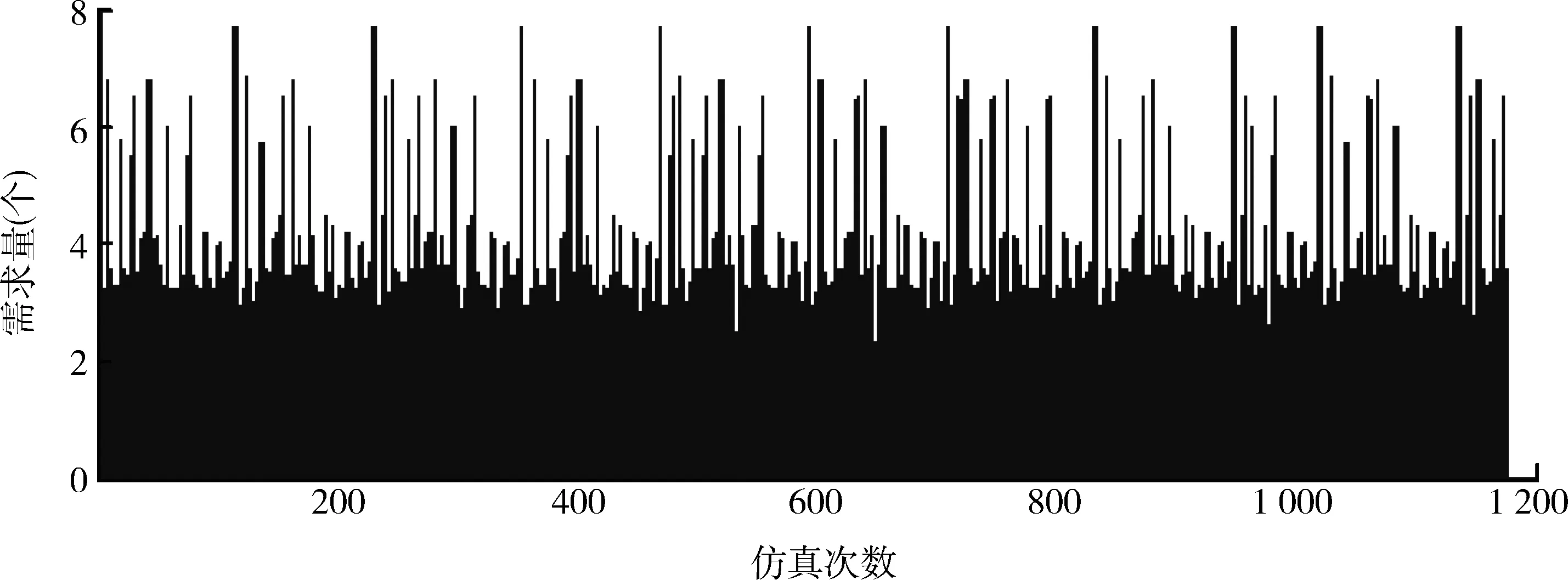
图3 备件需求量仿真图Fig.3 Simulation figure of spare parts demand

4 结束语

针对导弹装备故障数据样本量较小的情况，提出了基于最大熵原理与概率加权矩的分析方法，能够在确定概率分布的同时估计分布参数。该方法的优势在于适用范围较广，而且与基于经典矩的最大熵方法相比，对于样本量小于30的情形拟合效果更为理想。备件需求模型既分析了导弹装备工作期间发生情况，也考虑了导弹装备在停机期间及备件在储备期间也会发生故障的情况，更加贴近实际。

参考文献：

[1] PANDEY M D. Direct Estimation of Quantile Functions Using the Maximum Entropy Principle [J]. Structural Safety, 2000,22(1): 61-79.

[2] 俞礼军,严海,严宝杰. 最大熵原理在交通流统计分布模型中的应用[J].交通运输工程学报, 2001, 1(3): 91-94.

YU Li-jun, YAN Hai, YAN Bao-jie. Maximum Entropy Principle and Its Application in Probability Density Function of Traffic Flow [J].Journal of Traffic and Transportation Engineering, 2001, 1 (3): 91-94.

[3] HOSKING R M, WALLIS J R. Regional Frequency Analysis[M].New York: Cambridge University Press, 1997.

[4] TAN L, TANIAR D. Adaptive Estimated Maximum Entropy Distribution Model[J].Information Sciences, 2007,15(177):3110-3128.

[5] 俞礼军,徐建闽. 出行时间价值最大熵分布估计模型[J].交通运输工程学报, 2008, 8(1):83-96.

YU Li-jun, XU Jian-min. Estimation Models of Distribution Functions for Travel Time Value with Maximum Entropy Principle[J]. Journal of Traffic and Transportation Engineering, 2008, 8(1):83-96.

[6] 俞礼军, BenHeydecker. 基于概率加权矩与最大熵原理的交通流统计分布估计方法[J].公路交通科技, 2008, 25(2):113-133.

YU Li-jun, BenHeydecker. Probability Density method of Traffic Flow Based on Probability Weighted Moments and Maximum Entropy Principle[J]. Science and Technology of Road Transportation, 2008, 25(2):113-133.

[7] 朱坚民，郭冰菁，王中宇，等.基于最大熵方法的测量结果估计及测量不确定度评定[J].超重运输机械，2005，42(8)：5-8.

ZHU Jian-min,GUO Bing-jing,WANG Zhong-yu. Study on Evaluation of Measurement Result and Uncertainty based on Maximum Entropy Method[J].Journal of Electronic Measurement and Instrument,2005,42(8):5-8.

[8] YU X M,TONG L. Evaluation of Uncertainty in Measurement Based on the Maximum Entropy Method[J].Journal of Electronic Measurement and Instrument,2004,17(6):98-103.

[9] 葛阳, 宁剑平. 间断工作导弹装备维修备件需求量仿真模型[J].起重运输机械, 2010,22(12):42-48.

GE Yang, NING Jian-ping. Demand Simulation Model of the Missile Equipment Maintenance Parts in Discontinuous Work[J].Lift Transportation Mechanism, 2010,22(12):42-48.

[10] 金星, 文明, 李俊美. 寿命服从指数分布产品相关失效解析分析[J].装备指挥技术学院学报, 2002, 13(4):37-39.

JIN Xing, WEN Ming, LI Jun-mei. Correlative Failure Analysis on Exponential Distribution Manufacture[J].Journal of Academy of Equipment, 2002, 13(4):37-39.

[11] 程文鑫, 陈立强, 龚沈光. 基于蒙特卡洛法的舰船装备战备完好性仿真[J].兵工学报, 2006, 27(6):1090-1094.

CHENG Wen-xin, CHEN Li-qiang, GONG Shen-guang. Ship Equipment Operational Readiness Simulation Based on Monte Carlo Method[J].Acta Armamentarii, 2006, 27(6):1090-1094.

[12] 曹晋华, 程侃. 可靠性数学引论[M].北京:高等教育出版社, 2006.

CAO Jin-hua, CHENG Kan. Reliability Mathematics Generality Induction[M].Beijing: Higher Education Press, 2006.