高超声速边界层转捩和湍流计算问题

周恒

(天津大学 力学系，天津 300072)

0 引言

对飞行器的设计来说，在初步选定外形后，准确算出其气动力，包括升力、阻力、力矩，以及壁面热流等，是进一步设计的基础。早年这主要靠半经验的办法解决，要做大量的研究性实验和模型实验。但模型实验有很大的局限性，受制于在地面无法完全实现真实飞行时遇到的条件，无法做全尺寸实验，也无法同时满足所有的模型律。近年来，CFD(computational fluid dynamics)在研制各种飞行器中起到了越来越大的作用，已在很大程度上取代实验的作用。但在计算飞行器所受的摩阻及热载荷时，其结果的正确性有赖于对边界层转捩的预测能力和湍流计算能力。而如果飞行器因攻角较大而产生分离，则转捩预测不准还将影响到升力的预测。

边界层转捩预测及湍流计算这2个问题都是已历经100年之久还未彻底解决的问题。在2006年的Annual Review of Fluid Mechanics 的文章“Critical Hypersonic Aerothermodynamic Phenomena”[1]中引用NASA的Bushnell在1997年的话说：“历史上人类在预测所有高超声速(甚至超声速)飞行器的转捩时几乎从来没有成功过”。并指出，制约CFD在高超声速飞行器设计中应用的有四大因素，其中就有“模式化转捩及湍流的能力”。

1 转捩预测问题

1.1 转捩的基本概念及关键问题

以平板边界层为例。一般在前缘后有一段为层流，但其中有小的扰动。如果小扰动是增长的，则到下游某处，会经传捩过程而变为湍流，如图1所示。

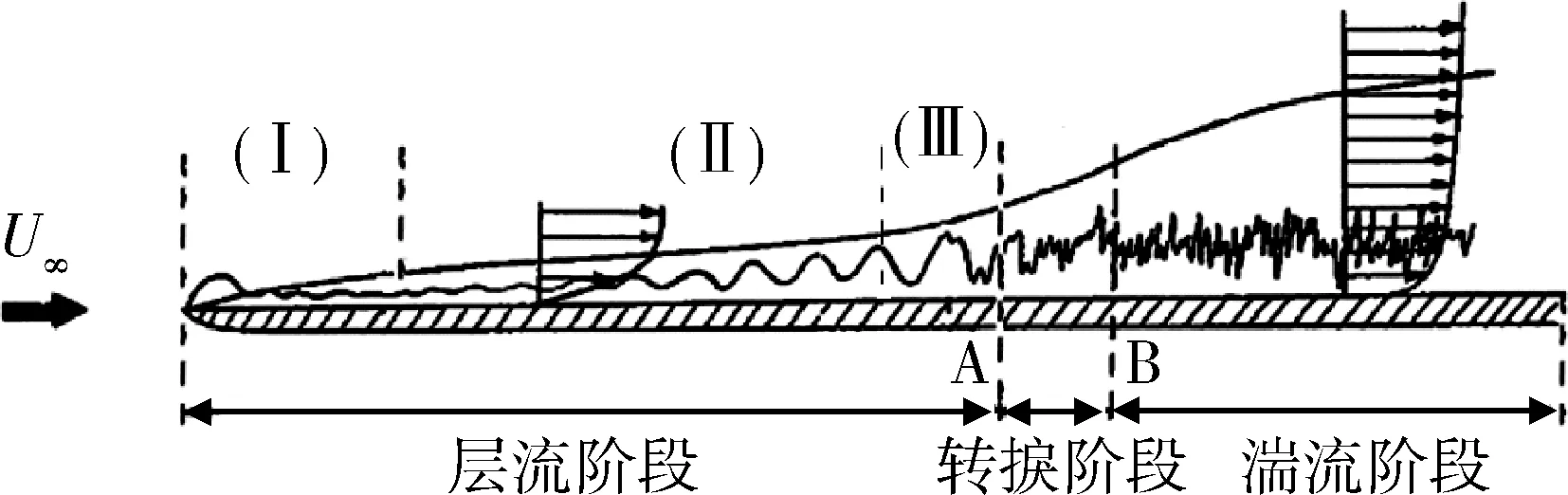
图1 边界层转捩过程示意图Fig.1 Sketch of the process of boundary layer transition

图2所示为转捩前后壁面摩擦系数和传热系数的变化。可见湍流段比层流段都要大数倍。如果转捩位置预测不准，显然会带来误差。实际上，转捩预测不准，对总摩阻的影响也可能不会太大，因为终究只占总值的一小部分。但对热防护设计来说则影响很大。因为，如实际已是湍流的地方仍按层流设计，则很可能会被烧坏，而实际仍是层流的地方按湍流设计，则会增加不必要的防热层的质量。此外，对有攻角的弹体，如果转捩线预测不准，则不仅会影响总阻力的计算，还会影响气动力矩的计算。

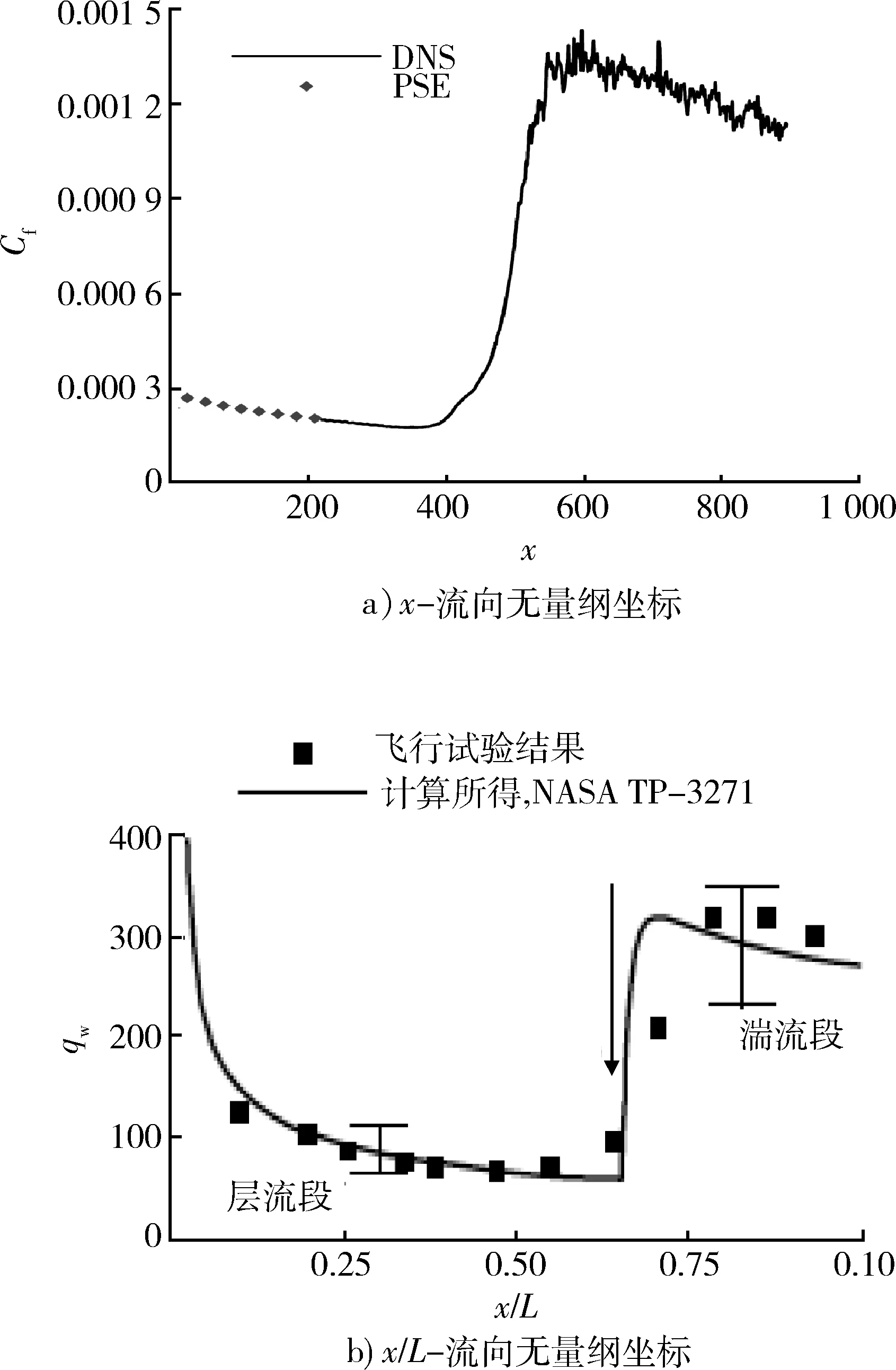
图2 转捩前后壁面摩擦系数Cf及传热系数qw的变化Fig.2 Change of friction Cf and heat transfer coefficients qw across the transition

转捩有2种。一种是如上所述由小扰动增长导致的转捩；一种是由大的扰动引起的转捩。前者要经历较长的小扰动演化过程，称自然转捩，而后者则在有了扰动后很快发生转捩，称by-pass转捩。高空飞行时的边界层一般是自然转捩。

自然转捩研究需解决的关键问题：

(1) 边界层中的小扰动是如何产生的——感受性问题

这个问题约从20世纪80年代开始，研究还不够充分。

对不可压流动，边界层外的扰动传播速度就是自由流速度，而边界层中的以不稳定波形式出现的小扰动，其传播速度小于自由流速度，二者不匹配。因而边界层外缘引起的边界层内的扰动不能直接转化为边界层内的不稳定波，而要通过与边界层内平均流在局部(尺度较不稳定波的波长小很多)发生较大变化处的相互作用才能在边界层内激发不稳定波。一般注意的是前缘处，边界层壁面的几何性质发生突变处，如2段不光滑(可以是一阶导数不光滑)相接处，或有粗糙度处。

对可压缩流，特别是高超声速流，边界层外的扰动除了有以自由流速度传播的外，还可以以快声波或慢声波的形式出现，其传播速度有可能和边界层内不稳定波传播速度相同或相近，可以直接或间接激发边界层内不稳定波。

(2) 小扰动在边界层中如何演化——扰动演化的线性及非线性理论

这个问题的研究比较充分，已有近100年历史。

已知边界层中的不稳定波，可以用线性或非线性稳定性理论，包括抛物化稳定性方程，研究其演化，特别是其放大过程。这时要求解稳定性方程。对不可压流，这类方程的边界条件是不难确定的，一般在壁面是不可滑移条件，边界层外为零边界条件。但对高超声速边界层，在壁面处多了一个温度条件，在边界层外会由于存在激波而较难处理(主要是马赫数非常高的高超声速边界层)。特别是不稳定波的演化对壁面温度条件较敏感，而壁面温度条件又往往很难确定，一般既不是定温，也不是绝热。

(3) 扰动演化至什么程度将触发转捩——转捩判据

边界层内扰动演化至何时会触发转捩，是转捩判据问题。由于转捩不仅依赖于扰动大小，而且还与扰动频率、形状等有关，增加了提出转捩判据的难度。国外目前还主要依靠经验或半经验方法。

高超声速边界层内温度可以很高，导致需考虑真实气体效应。好在需要较长时间在大气层中飞行的飞行器，其速度一般不会太高。如果Ma<7，则真实气体效应主要表现为气体的内能必须考虑振动能，比热将依赖于温度，但还不需要考虑分子的离解及化学反应。相对来说处理还不太难。

1.2 转捩预测方法

目前已有的转捩预测方法有2类：

(1) 基于线性稳定性理论的预测方法

基于线性稳定性理论的预测方法具有一定的合理性，如图1所示，在转捩发生前，要经历一段小扰动增长的过程。这一过程，占了从开始有小扰动到实际发生转捩的整个过程的大部分。但按原来的做法，要靠经验确定作为转捩判据的一个参数。因此，这是一种半经验法，国外称为eN法，N就是那个参数。而N的值，要针对某一类特定的流动，由经验得到。对eN方法的内容和应用可参考文献[2-3]。

在认为这一方法可靠的条件下，国外有人针对一类问题，将由其所得结果和边界层的某些参数，如边界层外沿的马赫数及边界层厚度等做关联，使得更便于纳入CFD的计算中，更便于工程技术人员的应用。

近年来，对基于线性稳定性理论的转捩预测方法做了较大改进，大大减少了对经验的依靠。

(2) 将转捩前的扰动演化植入湍流模式计算中，使得转捩和湍流合并计算。但扰动植入湍流计算这一点不太能令人信服，而且它有若干参数要靠经验确定，且对不同流动没有通用性。

美国和欧洲的航空航天界基本都采用eN方法。

1.3 eN方法及其改进简介

以超声速锥体边界层转捩为例(如图3所示)。

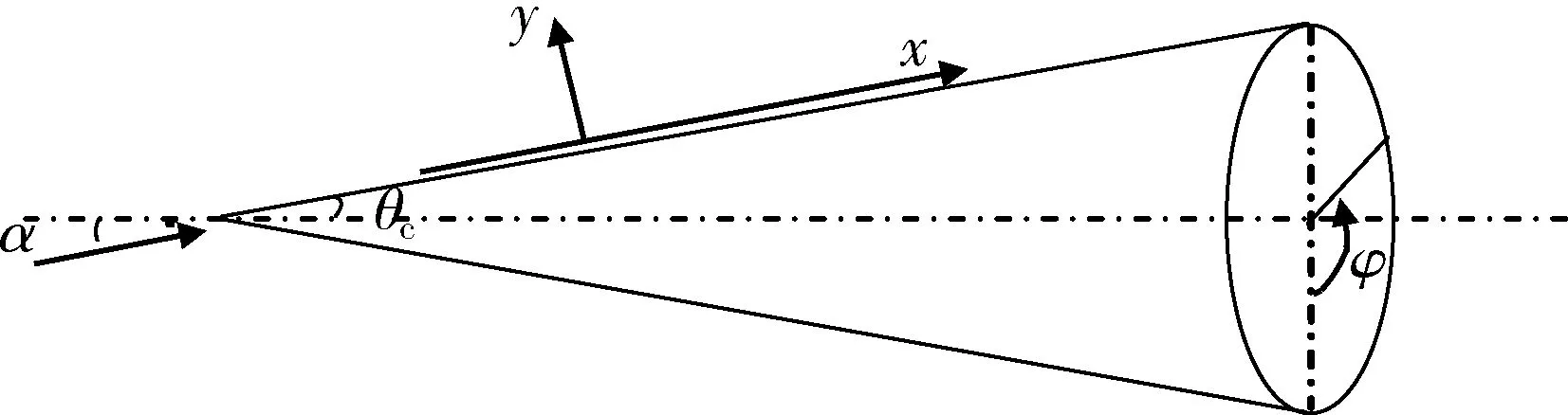
图3 小攻角锥体边界层转捩问题坐标图Fig.3 Coordinates used for the transition prediction of the boundary layer of a cone with small angle of attack

预测转捩要研究从每一个子午面出发的各种小扰动可能导致转捩的地方。

对每一个子午面，找出所谓的ZARF曲线(如图4所示)。其上的每一个点，都代表一个频率为F，在当地(对应横坐的标x值)放大率为0但却是局部最大(指频率相同但波数不同条件下)的扰动。

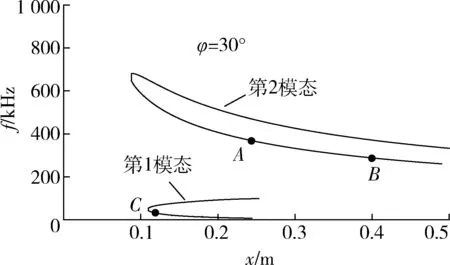
图4 某子午面中的ZARF曲线Fig.4 ZARF curves in a certain meridian plane

对ZARF曲线上每一点代表的扰动波，计算它沿其传播方向的放大倍数eN，N显然为x的函数。当N达到某一由经验确定的预设的值，则对应的x值就是一个可能的转捩位置。对所有ZARF上的点，可以找到一个可能转捩位置的点集合。其中对应于最小的x的点就决定了由该子午面出发的扰动导致的转捩点。由所有的子午面确定的转捩点就组成转捩线。

但是，在将这一方法用于超声速小攻角圆锥的转捩预测时，得到的转捩线如图3所示。其形状甚至在定性上也和一般实验所得结果不符。

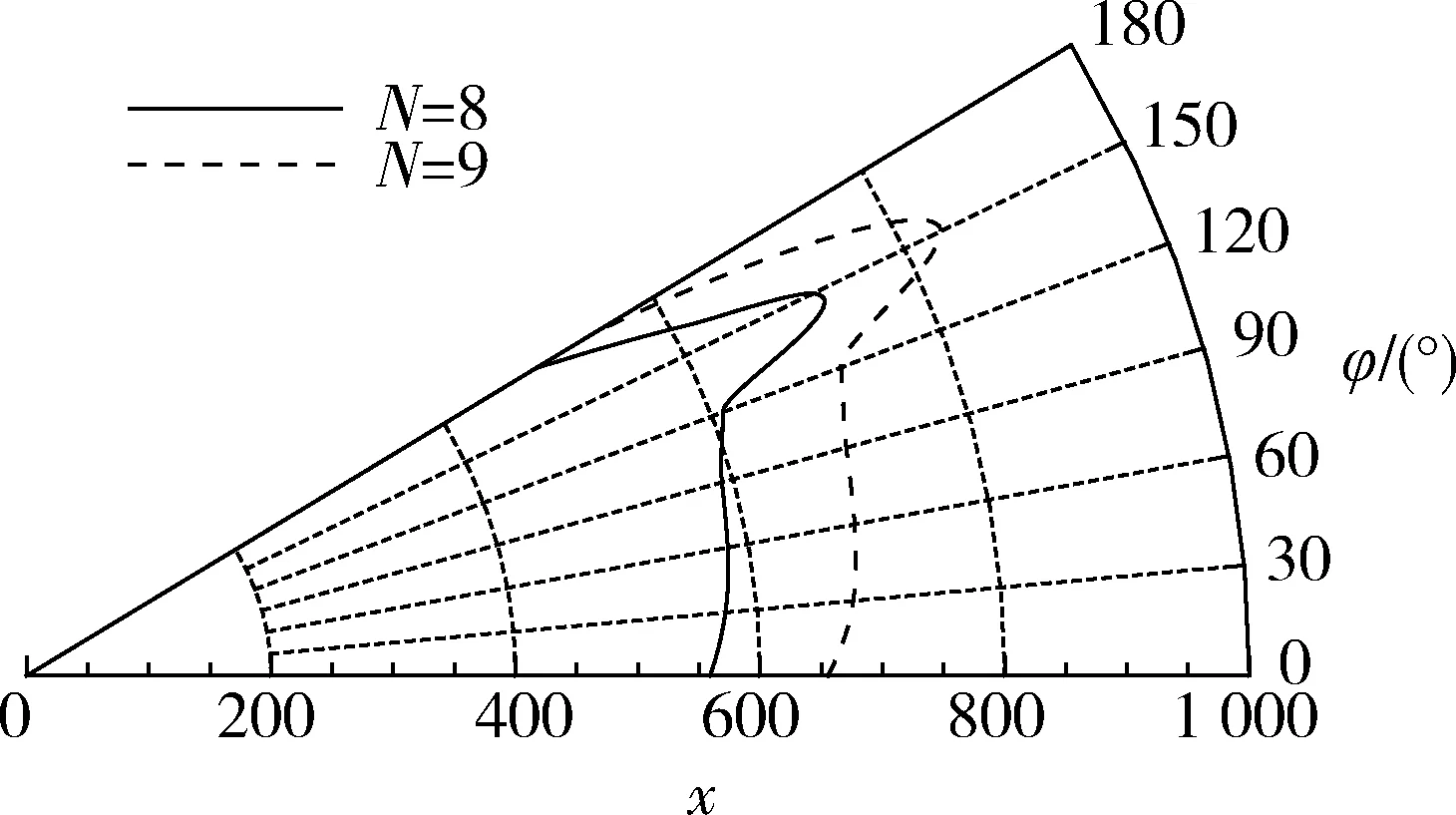
图5 某一Ma=6，攻角为1°的锥体边界层， 用传统eN法所得转捩线Fig.5 Transition line obtained by conventional eN method for the boundary layer of a cone with angle of attack 1° and Ma=6

一个合理的转捩预测方法，应该考虑前述与转捩有关的3个关键因素，而原来的方法只是考虑了其中的一个因素，即小扰动的增长过程。

针对原来方法的不足，文献[4]提出了2方面的改进意见。

(1) 考虑小扰动的实际产生机理

不从ZARF开始，而假设在离锥头不远的某一x处，所有子午面中的各种频率扰动的幅值均相同。对每一子午面，求所有从该x点出发的扰动波的幅值沿x的变化。当其幅值达到边界层外缘速度的0.015倍处，就认为该扰动会触发转捩。

在某一给定的初始扰动幅值下，得到了图6a)中的转捩线(Ma=6，攻角为1°锥体边界层)。而文献[5]在同样基本流条件下，采用在锥头下游不远处用壁面吹吸方法引入复杂扰动波系，得到了图6b)中的转捩线。二者十分相似。

文献[6]还用改进后的eN方法对其他能有实验结果的情况做了验算，结果也都满意。图7是其中的一个验证例子。

1992年，King做了一个超声速小攻角圆锥的转捩实验[7]。他所用的风洞有一个装置，在该装置不用的时候，风洞中的背景扰动主要是洞壁的湍流边界层发出的噪声扰动。而在该装置使用时，实验段前洞壁边界层的噪声扰动被抑制，此时的风洞称为静风洞，其主要背景扰动就是一般流动中的扰动。图8中带有实验点的2条线是对应于这2种情况的2种转捩线。靠上的是对应于静风洞的结果，靠下的是非静风洞的结果。对应于静风洞的转捩线更靠下游，这是因为这时的扰动更小。用上述改进后的eN方法，可以在适当选择扰动初值的情况下得到和实验很接近的结果。但对非静风洞情况，无论是原来的eN方法，还是改进了的eN方法，都不能得到甚至只是定性上相符的结果，见图8a)中最下面三角形点和图8b)中最下面的长方形点。文献[8]认为，这是因为对以声扰动为主的情况，应考虑边界层对声扰动的感受性。这时扰动将不是在锥头部被感受，而是在慢声波的波速和边界层中同频率的小扰动波的波速相同的地方被感受。采用这一因素后，得到的结果如图8c)中空心圆圈所示，和实验基本符合。要指出的是，完全符合是不可能的，因为风洞中声扰动在不同位置的幅值是不同的，而实验中并未给出这么全面的数据。计算中不得不做一定的假设。

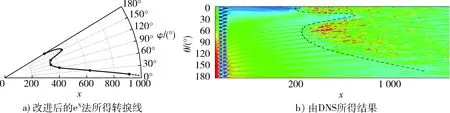
图6 不同方法得到的转捩曲线Fig.6 Transition curves obtained with different methods

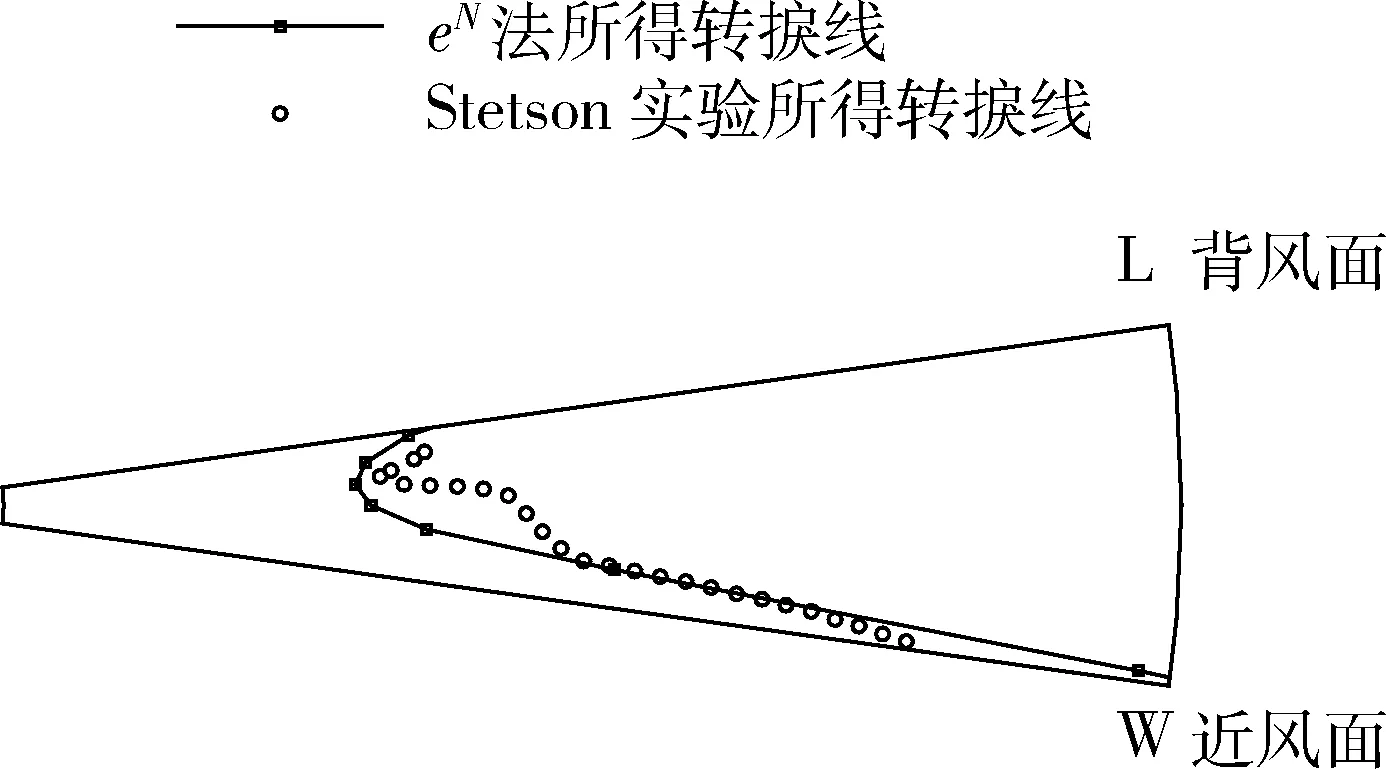
图7 另一情况与实验结果的比较Fig.7 Comparison with experimental observation for another case

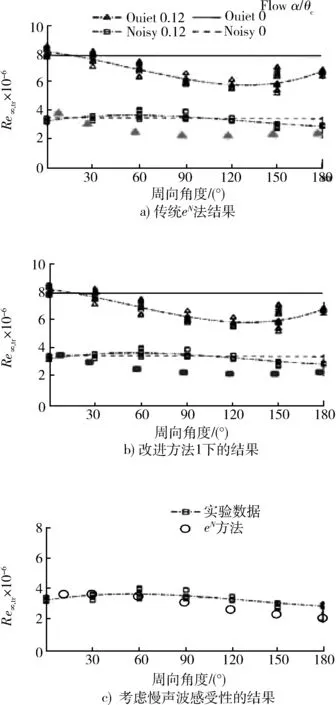
图8 实验与预测结果比较
Fig.8 Comparisons between experiments and theoretical predictions

(2) 给出基本不依赖经验的转捩判据

eN方法虽基于线性稳定性理论，但对从小扰动开始的自然转捩，在扰动小于0.01时，线性理论可以很好地描述扰动增长过程。而不少转捩的DNS结果显示，转捩开始时，一般扰动的大小也就在0.01～0.02之间。因此，建议以扰动幅值达到边界层外沿流速的0.015为转捩开始的判据。而不再像原来的eN方法中要针对不同流动靠实验或经验去确定作为转捩判据的N值。文献[9]对这一判据是否可靠做了进一步的验证，结果是肯定的。

2 湍流计算问题

2.1 目前湍流模式用于超声速/高超声速湍流边界层时的问题

对高超声速湍流边界层的湍流计算，目前还要靠湍流模式。最常用的有：①代数模式，如Baldwin-Lomax (B-L)模式，Cebeci-Smith模式；②一方程模式，如Spalart-Allmaras(S-A)模式；③ 两方程模式，如k-ε模式，k-ω模式及其改进型，Menter SST模式等。这些的共同特点是，模式最终都提供一个涡粘系数。代数模式最容易用，其次是一方程模式，再次是两方程模式。 C. J. Roy & F. G. Blotther[10]在2006年， P. A. Gnoffo等[11]以及J. L. Brown[12]在2013年分别将各种模式计算结果与实验结果进行对比，结果发现，如果边界层没有由于和激波相互作用而发生分离，则对壁面压力和壁面剪应力，各种模式都能给出还算合理的结果，与实验结果相比的误差在10%以内。但对壁面热流，则各种模式和实验结果的差别都较大，在某些局部地方，甚至可达200%。出乎意料的是，代数模式在热流计算上，比一方程和两方程模式的结果更好。但如果边界层由于激波干扰而出现分离，则代数模式就会失效。

但是，只以实验结果为根据，很难分析上述各种模式不足的原因。近年来由于计算机及计算技术的发展，已可以对湍流边界层做湍流的直接数值模拟(DNS)。而DNS的结果可以提供详尽的数据。而且，对高超声速边界层做实验，壁面的热边界条件很难确切给出。一般它既不是绝热，也不是定温。即使其他实验条件都相同，壁面的材料传热系数及壁面内部温度的不同，也可导致不同的壁面热流条件。而DNS则可确切规定壁面温度或热流条件。因此，用DNS结果和用模式计算结果做对比，则可避免由于壁面热边界条件不完全对应带来的不确定性。

目前对湍流做直接数值模拟，还只能做雷诺数比较小的。但是，有2种因素使得这一限制影响减小。一是对飞行在高空，例如30 km以上的情况，单位长度雷诺数实际不大。因为雷诺数Reunit=v/ν=vρ/μ，其中v是速度，μ是粘性系数，ρ是密度。对高超声速而言，v虽然很大，比亚声速可以大一个量级，但在30 km以上的高空，密度约是地面空气密度的1/67，因此单位雷诺数比在地表附近做亚声速飞行的要小得多。二是战术导弹的尺寸一般不太大，因此实际雷诺数也不会很大。

上面列举的两方程模式，其最终所给出的涡粘系数，都是基于涡粘系数μT正比于k2/ε的假设，即μT=Ck2/ε，其中k是湍动能，ε是湍动能的耗散速度，C为常数。文献[13]对Ma为6，壁面温度tW为来流温度5.5倍的平板边界层分别用DNS和几种模式计算k和ε，结果发现k的分布还相差不多，只是量的差别，而ε的分布则定性上都差别很大，见图9a),9b)。而用不正确的ε组合出正确的涡粘系数，从道理上是说不通的。文献[5]也针对Ma为6的平板湍流边界层，把由DNS得到的k与ε代入k-ε模式的公式所算出的涡粘系数(图9c)中的实线)，与直接由DNS结果推出的涡粘系数(图9c)中的空心圆连线)进行比较，发现无论是定量还是定性都相差很多。可见原来的基本假定有问题。近年来，有不少研究发现，对平板边界层、槽道流及圆管流动这类有剪切的壁湍流，沿壁面方向可分为若干层，每一层的湍流动力学特征不同。因此μT=Ck2/ε这一假设并不正确。

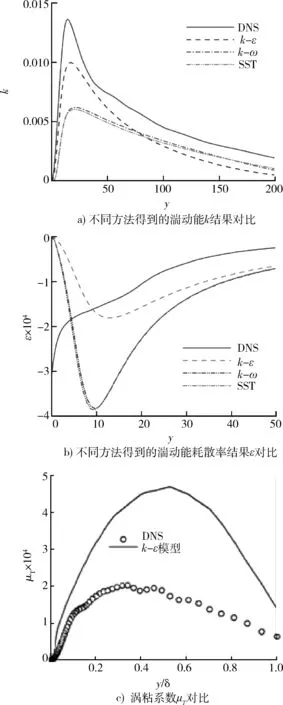
图9 湍动能k、湍动能耗散率ε及涡粘系数μT的比较Fig.9 Comparisons for the turbulent kinetic energy k, dissipation rate ε of the turbulent kinetic energy and the eddy viscosity μT

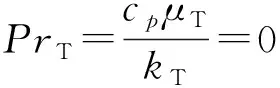
2.2 对B-L模式所做的改进

由于航天用飞行器外形相对航空飞行器简单，很多部位由直线、平面、锥体或接近于他们的几何形状组成。在没有分离的地方，边界层湍流接近于平衡或充分发展湍流，B-L模式可用，而B-L模式是最便于应用的湍流模式。因此，B-L模式迄今在航天系统还常被采用。据此，文献[13]决定先针对B-L模式，看是否有改进的可能。他们在对高超声速平板湍流边界层做DNS的结果分析的基础上发现，传统的B-L模式有3个方面要做改进。

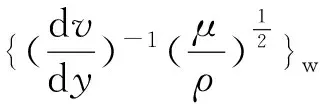
(2) 湍流Prandtl数不应是常数。层流状态下的粘性和传热，其起因都是分子间的碰撞引起的，机理相同，因此其系数之比为常数的假定合理。但涡粘性和涡传热是流体微团间的动量和热量传递。虽然最直接的原因都是由接触处的分子碰撞导致，但在微团内动量传递比热量传递效率高。例如设想一个一维的情况如图10 所示。有2个微团，各有速度v1，v2及温度T1，T2，且v1>v2。当微团1追上微团

2，动量及热量传递开始。如果不考虑流体的压缩性，则动量传递瞬间完成，两微团的速度立即变得相等。但热量传递不可能瞬间完成，而仍要通过热扩散完成。三维情况二者的差别要小一些。湍流强度越大的地方，二者差别越大。根据这一考虑，他们以边界层中湍动能的分布(各种参数下不完全相同，但差别不大)为依据，给出了一个修正的表达式。

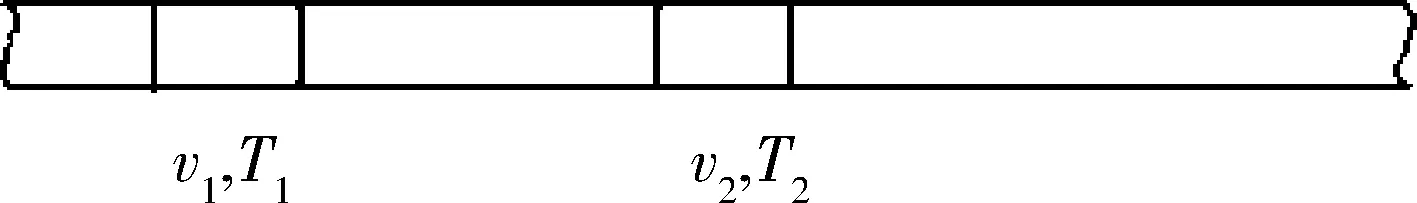
图10 2流体微团相碰情况Fig.10 Sketch for the collision of two fluid lumps

(3)

对冷却壁，要对B-L模式中的混合长公式在壁面附近做一定的修正。经过这3个修正之后，B-L模式不仅能给出更精确的壁面摩擦系数和壁面传热系数，而且也能给出更精确的整个平均流和平均温度的剖面。图11是一个例子。

图11中，Ma=6，壁面温度Tw=0.61Taw，Taw为绝热壁温度。DNS为直接数值模拟结果，BL为传统BL模式结果，modify1为仅第一种改进后的结果，modify2为仅有1，2两种改进的结果，modify3为3种改进都采用后的结果。

3 结束语

需要指出的是，迄今所有湍流模式，都不能同时给出精确的壁面摩擦系数、壁面传热系数和整个平均流和平均温度的剖面。而对有分离的问题，如果分离不是由入射激波或压缩拐角等引起的，而是由于如攻角较大等因素引起的，则分离位置与分离前的边界层厚度等有关。如果分离前的平均流剖面不准确，则计算出的分离位置一般也不准确。

如前所述，对有分离的情况，代数模式不能用。是否可能对其再做改进，以使之能用，还是必需用带方程的模式，还需要研究。而如必需用带方程的模式，则它们也需要有实质性的改进。

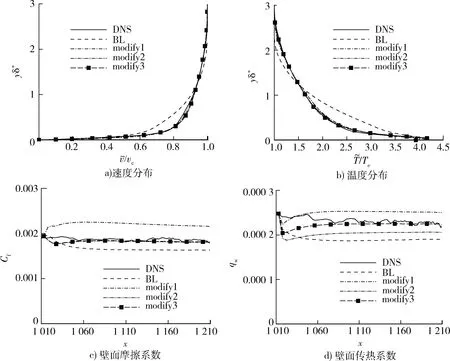
注：图中横坐标分别为：a)无量纲流向平均速度；b)无量纲温度；c)无量纲流向坐标；d) 无量纲流向坐标图11 平板湍流边界层的速度、温度、壁面摩擦系数及壁面传热系数的分布Fig.11 Distribution of the mean flow velocity, temperature and heat transfer coefficient at the wall

参考文献：

[1] Bertin John J, Cummings Russell M. Critical Hypersonic Aerothermodynamicc Phenomena[J]. Annul Review of Fluid Mechanics, 2006, 38：129-157.

[2] CEBECI T, STEWARTSON K. On Stability and Transition in Three-Dimensional Flows[J]. AIAA, 1980, 18(4): 398-405.

[3] CEBECI T, SHAO J P. CHEN H H, et al. The Preferred Approach for Calculating Transition by Stability Theory[C]∥ Proceeding of International Conference on Boundary and Interior Layers, ONERA, Toulouse France,2004.

[4] SU Cai-hong, ZHOU Heng. Transition Prediction of a Hypersonic Boundary Layer Over a Cone at Small Angle of Attck—with the Improvement ofeNMethod[J]. Science in China Series, 2009,52(1):115-123.

[5] LI X L, FU D X, MA Y W. Direct Numerical Simulation of a Spatially Evolving Supersonic Turbulent Boundary Layer at Ma=6[J]. Chinese Physics Letters, 2006,23(6):1519-1522.

[6] SU Cai-hong, ZHOU Heng.Transition Prediction for Supersonic and Hypersonic Boundary Layers on a Cone with Angle of Attack[J]. Science China Physics, Mechanics & Astronomy, 2009, 52 (8):1223-1232.

[7] KING R A. Three-Dimensional Boundary-Layer Transition on a Cone at Mach 3.5[J]. Experiments in Fluids, 1992(13):305-314.

[8] SU Cai-hong, ZHOU Heng. Transition Prediction of the Supersonic Boundary Layer on a Cone Under the Consideration of Receptivity to Slow Acoustic Waves[J]. Science China, Physics, Mechanics & Astronomy, 2011, 54(10):1875-1882.

[9] SU Cai-hong. The Reliability of the Improved eNMethod for the Transition Prediction of Boundary layer on a flat Plate[J]. Science China Physics, Mechanics & Astronomy, 2012, 55 (5)：837-843.

[10] ROY C J,BLOTTNER F G. Review and Assessment of Turbulence Models for Hypersonic Flows[J]. Progress in Aerospce Sciences, 2006,42:469-530.

[11] GNOFFO P A, BERRY S A, Van Norman J W. Uncertainty Assessment of Hypersonic Shock Wave-Boudary-Layer Interaction at Compression Corner[J]. Journal of Spacecraft and Rockets, 2013, 50(1):69-95.

[12] BROWN J L. Hypersonic Shock Wave Impingement on Turbulent Boundary Layer: Computational Analysis and Uncertainty[J].Journal of Spacecraft and Rockets, 2013, 50(1):96-123.

[13] DONG Ming, ZHOU Heng.The Improvement of Turbulence Modeling For the Aerothermal Computation of Hypersonic Turbulent Boundary Layers[J]. Science China Physics, Mechanics & Astronomy, 2010, 53(2)：369-379.