制导炸弹弹体结构可靠性分析与应用

樊富友，于娟，陈明，杜冲，余里成，刘剑霄

(1.中国兵器集团公司 长沙机电产品研究开发中心，湖南 长沙 410100; 2.中航光电科技股份有限公司，河南 洛阳 471003)

0 引言

制导武器一般包括制导导弹(导弹)、制导炸弹、制导水雷及制导鱼雷等多种精确制导武器。制导炸弹和导弹的主要区别在于制导炸弹自身无动力系统，需借助飞机投掷，通过制导、控制系统飞向目标，导弹依靠自身的动力系统和制导、控制系统飞向目标。制导炸弹弹体通常称为制导炸弹的“躯干”，是指构成制导炸弹外形，连接和安装弹上各个装置的整体结构。弹体是制导武器的主体部分，通常由多个舱段连接而成，并能承受各种载荷，同时保证制导炸弹能正常执行任务。根据功能特点要求弹体结构有尽可能小的质量，尽可能大的空间，尽可能高的弹体利用率，尽可能高的外形准确度和表面质量，以减小气动阻力。

1 弹体结构可靠性分析

1.1 弹体结构可靠性

结构可靠性是结构在给定的使用条件下和给定的使用寿命内不产生破坏或功能失效的能力[1]。结构可靠度是结构在规定的时间内，规定的条件下完成预定功能的概率。弹体结构可靠性作为制导炸弹系统内的一个指标，可用于制导炸弹经过发射前准备，从出厂交付部队使用，期间反复经历包装、运输、装卸、存放、检测、维修、训练及发射等过程[2]，不出现致命故障的概率来描述。

弹体结构可靠性分析是用应力与强度的数量统计方法，研究强度问题的随机量，确定结构所承受的载荷和两者之间的关系，定量地评价弹体结构可靠性水平。弹体结构强度可靠性设计过程流程图如图1所示。

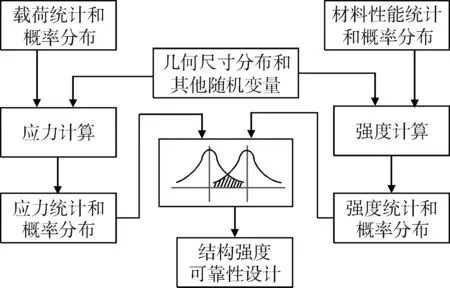
图1 结构强度可靠性设计流程图Fig.1 Design flow figure of reliability of structure strength

1.2 弹体结构可靠性计算

目前，机械载荷以静载荷为主，在静载荷设计的基础上，用动载荷进行“后设计”校核，热载荷(热环境参数)以它造成结构件的热响应来分析[3]。

弹体结构设计中，零件的应力小于零件强度时，不发生故障或失效[4]。按结构问题特点，结构可靠度为结构强度大于结构所承受载荷的概率。若强度用S表示，载荷用L表示，PS和Pf可表述为

PS=P(S-L≥0)=P[(S/L) ≥1]，

Pf=P(S-L<0)=P[(S/L) <1].

令f(S)为应力分布的概率密度函数、g(δ)为强度分布的概率密度函数，如图2所示，应力与强度的概率分布曲线发生干涉。

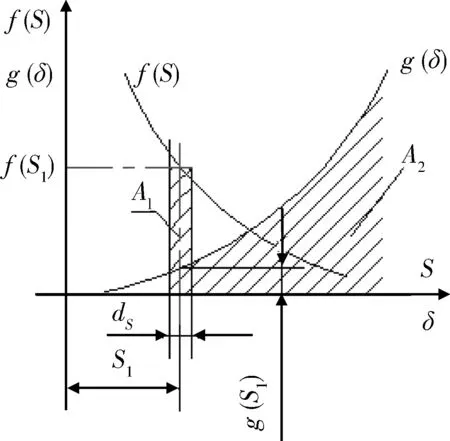
图2 应力-强度分布干涉图Fig.2 Stress strength distribution interference figure

应力值S1落在宽度为dS的小区间内的概率等于该小区间所决定的单元面积A1，即

A1=f(S1)dS=P[(S1-dS/2)≤S≤(S1+dS/2)].

强度δ大于应力S1的概率为

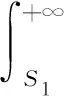
若弹体结构中任何一个舱段结构失效，则弹体结构失效，那么弹体各舱段间为串联联接；若只有在弹体的所有舱段失效后，弹体结构才会失效，那么弹体各舱段间为并联联接。对实际舱段结构而言，只要舱段中个别元件或部分元件失效，则认为舱段失效，通常，弹体结构舱段间为串联联接[5]。

制导炸弹弹体结构的可靠性指标，可表示为[6-8]

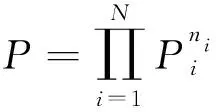
式中：Pi为第i个结构组件不破坏的概率；ni为结构中相同组件数；N为结构组件类型数。

结构组件不破坏的概率(满足强度条件μp=ηf(μ1+3σ1)按下式确定[3][9]：

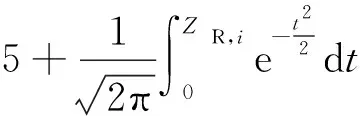
式中：ZR,i为第i个结构部件的可靠性系数；μs,i为第i个结构部件材料强度极限的数学期望；σs,i为第i个结构部件材料强度极限的均方根偏差；μl,i为第i个结构部件载荷值的数学期望；σl,i为第i个结构部件载荷值的均方根偏差。

σs,i=μs,iCvs，

σl,i=μl,iCvl，

式中：μp,i为第i个结构部件材料强度极限；η为剩余强度系数；f为安全系数；Cvl为载荷变差系数；Cvs为材料性能变差系数；

1.3 弹体结构可靠性参数

1.3.1 参数的统计处理

(1) 载荷的统计分析

载荷作用于零件或部件中会引起变形和应变等效应。若不超过材料的弹性极限，则由静载荷引起的效应基本保持不变，而由动载荷引起的效应则是随时间而变化。大量统计表明，静载荷一般用正态分布描述，动载荷一般用正态分布或对数正态分布描述。

(2) 材料的统计分析

金属材料的抗拉强度σb,屈服极限σs能较好符合或近似符合正态分布；多数材料的延伸率δ符合正态分布；剪切强度极限Τb与σb有近似关系，故近似于正态分布。疲劳强度极限有弯曲、拉压、扭转等，大部分材料的疲劳强度极限服从正态分布或对数正态分布，也有的符合威布尔分布。多数材料的硬度近似于正态分布或威布尔分布。

金属材料的弹性模量E，剪切弹性摸量G及泊松比μ具有离散性，可认为近似于正态分布。

(3) 几何尺寸

由于加工制造设备的精度、量具的精度、人员的操作水平、工况、环境等影响，使同一零件同一设计尺寸在加工后也会有差异。零件加工后的尺寸是一个随机变量，零件尺寸偏差多呈正态分布。

1.3.2 参数数据的计算

(1) 剩余安全系数

一般等于或略大于1，使强度略有储备，但不宜过大，以免造成弹体结构质量偏大。

(2) 安全系数

安全系数是制导炸弹结构设计中的一个重要参

数，它是一个带有经验性质的数据，不但受外载荷、结构强度及失效模式的控制，而且还要受材料、加工质量、结构可靠度指标、特定的使用要求等综合因素的影响，它的大小会直接影响到结构质量和可靠度，关系到制导炸弹的性能。

地空导弹安全系数一般取1.2～2.0；制导炸弹的安全系数一般取1.25～2.0，金属构件一般取1.2～1.3，复合材料构件安全系数一般取1.9～2.0。

(3) 可靠性安全系数[10-11]

把安全系数与可靠性联系起来产生的可靠性安全系数，是在结构强度变差系数和载荷变差系数的基础上，用95%的概率下限强度与99%的概率上限载荷之比求得

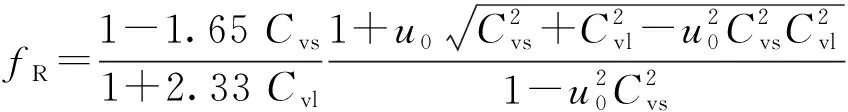
式中：fR为可靠性安全系数；u0为可靠度系数。

这是按照出现概率为5%的最小强度与1%最大载荷之比来定义的可靠性安全系数。

(4) 材料特性变差系数

材料性能变差系数是由它的数学期望与均方根偏差求得，而均方根偏差与数学期望，是设计部门依据制导炸弹所用材料的机械性能、物理性能，以及这些性能随温度变化，测试统计的数据。

制导炸弹所用材料变差系数，一般取值为0.02～0.16。

常用材料特性的变差系数如表1所示。

(5) 载荷变差系数

载荷变差系数在制导炸弹设计初期可用类比法，参考以前类似型号数据或飞航导弹数据；也可用计算飞行弹道的原始数据散布特性求得，根据某一制导炸弹部件选定的设计情况，通过载荷近似认为正态分布的性质，采用3σ原则求得。

载荷变差系数的取值范围一般为0.02～0.22。轴压和弯扭复合载荷取0.2；按分布载荷计算取0.1，内压或外压取0.02[1]。

根据气动吹风试验、靶场试验等统计数据，得出制导炸弹载荷因素拟合出服从正态分布的标准解析分布，并得出相应的分布参数。载荷分布类型及变差系数如表2所示。

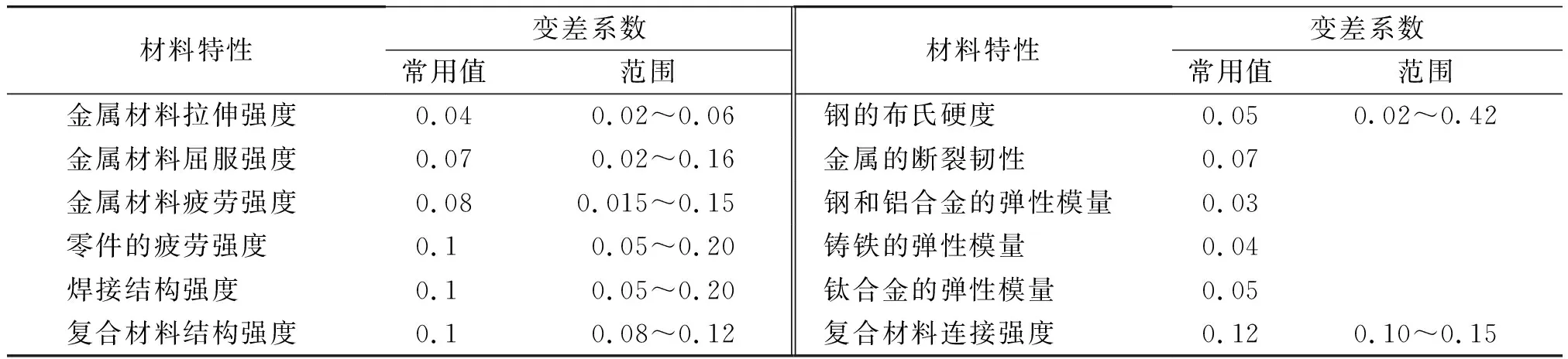
表1 常用金属材料的变差系数

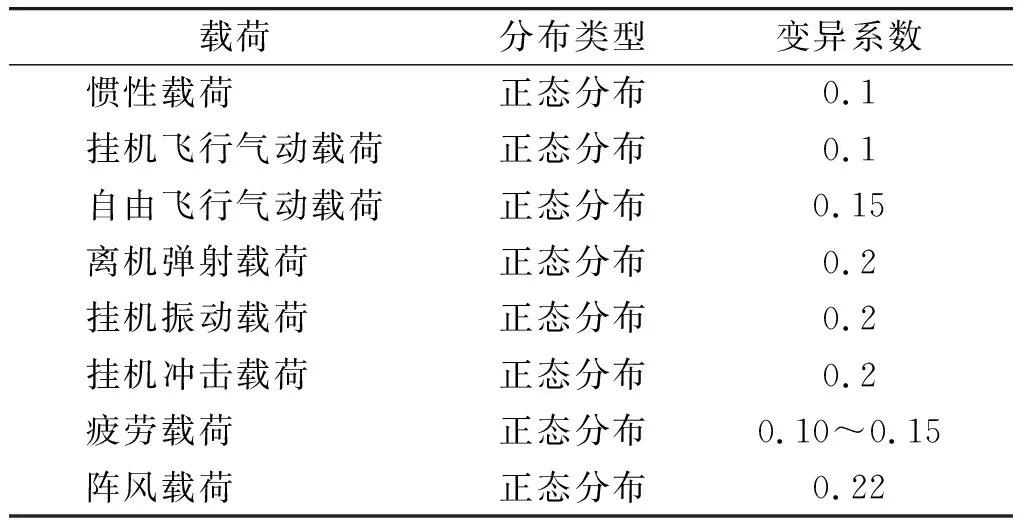
表2 载荷变差系数

2 提高弹体结构可靠性的途径

结构失效可定义为“在规定的使用条件下，结构丧失其规定的功能”，在《飞机结构强度与刚度规范》中，将“由于结构某些元件分离、断裂、失稳、过度变形和异常畸变而导致结构降低其承受规定载荷能力的现象”称为结构失效[12]。

弹体结构是一个复杂结构系统，有多种失效模式，如强度刚度失效、密封失效、老化失效、疲劳失效等。制导炸弹零部件的静强度刚度失效模式以屈服、失稳、断裂、变形等为主。因此，要提高弹体结构可靠性需要从以下几方面入手。

2.1 载荷

载荷是制导炸弹结构可靠性设计和计算的原始数据，载荷计算取决于制导炸弹飞行弹道及弹道上典型计算点的确定。载荷是随机变量，寻求制导炸弹使用和飞行中的载荷均值、标准偏差或变差系数，分析载荷的性质，使这些载荷能真实反映制导炸弹在使用和飞行过程中的真实情况。载荷不准，给制导炸弹结构设计会带来大的失误，造成盲目设计，使制导炸弹的质量超标或使制导炸弹飞行中遇到实际大载荷而破坏。同时载荷变差系数反映载荷散布的大小，对于具体部件要具体分析。变差系数选大了，保证了弹体结构的可靠度，增大了弹体结构的安全系数，但造成了制导炸弹质量的增大；变差系数选小了，满足了质量最轻的要求，同时降低了弹体结构可靠度。

2.2 传力路线的合理安排

在进行制导炸弹弹体结构可靠性设计时，应合理安排受力构件和传力路线，使载荷合理地分配和传递，减少或避免构件受附加载荷。结构设计应避免传力路线上构件不连续；尽量减少传力路线拐折；传力路线交叉时，一般构件应给主要受力构件或受载严重的构件让路。

2.3 材料的选择与控制

在进行结构设计时，材料的选择要考虑零部件的功能用途，特别是作用在部件上的气动载荷和温度等因素，在气动和热条件下材料机械性能变化大，更要选准材料性能变差系数。整个零部件各种材料的性能要互相匹配，做到等强度设计。材料选择的基本原则应要全面满足结构完整性要求，应根据各项设计要求和材料所具有的性能，进行综合权衡。元件材料的机械性能应与元件的受力一致，如承受中等载荷的元件，应选机械性能适中的铝、镁合金，不宜选用高强度的合金钢。

2.4 结构细节设计的一般原则

(1) 构件应有足够的刚度，防止在重复载荷的作用下，因过度变形引起裂纹；

(2) 相互连接零件的刚度及连接刚度应相互匹配，变形协调，以防止牵连变形促使连接部位开裂；

(3) 次要构件应合理地与主承力构件连接；

(4) 采用适当的补偿件，减少连接部位的强迫装配应力；

(5) 尽量减少由于开口，切槽，钻孔，焊接，尖角和壁厚差导致的应力集中；

(6) 控制螺纹连接件的预紧力矩；

(7) 对制导炸弹结构中的关键承力如(吊挂、舱连接件、翼面及舵面接头等)，可采用对材料或零件的极限应力采用降额设计；

(8) 应考虑电化学腐蚀的影响，尽量减少电位差大的不同金属零件的直接接触；

(9) 结构设计中应考虑结构相容性问题；

(10) 应避免零件上多个应力集中因素相互叠加而引起复合应力集中等。

全面分析制导炸弹在使用中所承受的各种载荷性质，有针对性地进行结构可靠性设计。

2.5 弹体结构可靠性优化设计

制导炸弹结构设计与它的参数优化密切相关，制导炸弹的制造与所选择的最佳方案及强度计算有关。在确定最佳结构设计方案时，必须考虑结构可靠性优化。

一般进行弹体结构可靠性优化[13]，即在给定制导炸弹结构总体的可靠度之下，进行制导炸弹各个舱段最佳结构可靠度计算，然后进行各个舱段之间的可靠度的优化配置；在满足结构总体可靠度的情况下，选出最佳安全系数，使弹体的质量最小。结构质量与可靠性之间的关系可用图3表示。

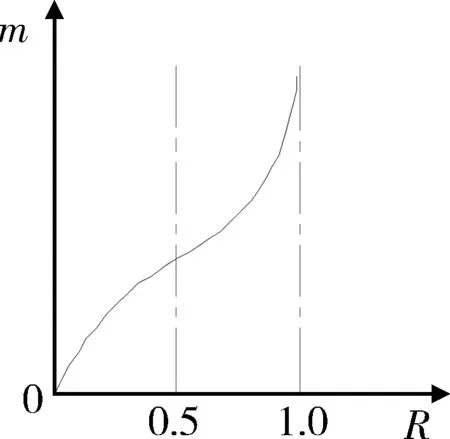
图3 结构质量与可靠度的关系曲线Fig.3 Curve of relationship between structure quality and reliability

当可靠度大于0.5时，可靠度R与结构质量m的近似关系为

m=k(1-R)-α.

k和α为待定参数，与具体的结构有关，具体计算方法参考相关文献[5]。

3 结束语

弹体结构可靠性设计是以概率论和数理统计为基础发展起来的一种设计方法。一般将载荷、材料性能、环境等视为一定分布规律的统计量，计算出弹体结构可靠度。弹体结构可靠性设计可以加强结构可靠度，减少结构设计盲目性，使结构设计更加合理、科学。目前，由于结构可靠性设计还处于发展和逐步完善的阶段，所以还存在不少问题和困难，如有的结构给不出载荷偏差，有的结构给不出强度偏差，或由于强度试验数据较少，得到的强度统计数据有较大的误差，仍须按安全系数或参照安全系数法进行设计和计算。然而，随着结构设计日益科学化、现代化，结构可靠性设计与计算已受到人们越来越多的重视，进行结构可靠性分析与设计是必然趋势。结构可靠性设计与计算方法不成熟、不简单、不实用，试验数据不充分，都会影响其推广。未来能将结构可靠性设计与优化的数学模型结合起来，需要探索的路很漫长。

参考文献：

[1] 张骏华,徐孝诚,周东升,等.结构强度可靠性设计指南[M].北京：宇航出版社，1994.

ZHANG Jun-hua, XU Xiao-cheng, ZHOU Dong-sheng,et al. Guide to Reliability Design of Structure Strength[M]. Beijing:Astronautic Publishing House, 1994.

[2] 樊富友，余志超，陈明，等.制导炸弹贮存可靠性分析与探讨[J].装备环境工程，2013，10(4):102-105.

FAN Fu-you, YU Zhi-chao, CHEN Ming, et al. Analysis and Discussion on Storage Reliability of Guide Bombs[J]. Equipment Enviromental Engineering, 2013，10(4):102-105.

[3] 曲之津.地(舰)空导弹弹体结构可靠性分析[J].现代防御技术，2001，29(2):19-22.

QU Zhi-jin. Structural Reliability Analysis of the Surface(ship) to Air Missile Body[J].Modern Defence Technology，2001，29(2):19-22.

[4] 宋保维.系统可靠性设计与分析[M].西安：西北工业大学出版社，2000.

SONG Wei-bao. Reliability Design and Analysis of System[M]. Xian: Northwestern Polytechnical University press,2000.

[5] 王善,何健.导弹结构可靠性[M].哈尔滨：哈尔滨工程大学出版社，2002.

WANG Shan,HE Jian. Missile Structure Reliability[M].Harbin: Harbin Engineering University Press,2002.

[6] 张伟.结构可靠性理论与应用[M].北京：科学出版社，2007.

ZHANG Wei. Theory and Application of Structural Reliability [M]. Beijing: Science Press，2007.

[7] 施久玉.概率论与数理统计[M].哈尔滨：哈尔滨工程大学出版社，2000.

SHI Jiu-yu. Probability Theory and Mathematical Statistics[M].Harbin: Harbin Engineering University Press,2000.

[8] 刘混举.机械可靠性设计[M].北京：国防工业出版社，2010.

LIU Hun-ju. Mechanical Reliability Design[M]. Bei-jing : National Defense Industry Press, 2008.

[9] 张兴有.飞航导弹弹体结构可靠性分析[J].战术导弹技术，2010(5):58-61.

ZHANG Xing-you. Structural Reliability Analysis of the Winged Missile Body[J]. Tactical Missile Technology，2010(5):58-61.

[10] 张骏华.结构可靠性设计与分析[M].北京：宇航出版社，1989.

ZHANG Jun-hua. Reliability Design and Analysis of Structural[M]. Beijing: Astronautic Publishing House, 1989.

[11] 胡昌寿.航天可靠性设计手册[M].北京：机械工业出版社，1999.

HU Chang-shou. Aerospace Reliability Design Handbook[M].Beijing: Mechanical Industry Press, 1999.

[12] 刘文珽.结构可靠性设计手册[M].北京：国防工业出版社，2008.

LIU Wen-ting. Mechanical Reliability Design Handbook[M]. Beijing: National Defense Industry Press, 2008.

[13] 何水清，王善.结构可靠性分析与设计[M].北京：国防工业出版社，1993.

HE Shui-qing, WANG Shan. Reliability Design and Analysis of Structural [M]. Beijing : National Defense Industry Press, 1993.