大型定子叶片铸件的数字化测量及误差评定

时可可， 潘为民， 郭志强， 雷贤卿， 叶 欣

（1. 河南科技大学机电工程学院，河南 洛阳 471003；2. 南车洛阳机车有限公司，河南 洛阳 471002）

近年来，数字化测量技术的不断丰富和发展为航空、航天、船舶、汽车及模具工业的发展提供了强有力的支持；随着现代工业产品的性能、外形等方面的要求越来越高，使得复杂曲面零件在现代工业中得到了日益广泛的应用，而对该类零件的反求和精度检验都离不开对复杂曲面的数字化测量[1]。数字化测量是指采用先进测量设备，获取实物模型表面若干组点的几何坐标值的过程[2]。目前，用来采集物体表面数据的主要数字化测量设备有：计算机断层扫描仪(computed tomography，CT)、三坐标测量机（coordinate measuring machine，CMM）和三维激光扫描仪（three dimensional laser scanner）等。

目前对于数字化测量技术的应用主要集中在实体场景的三维重现、产品的逆向设计和虚拟现实等方面，在误差检测和评定方面，Menq等[3]提出一种在CAD模型指导下检测表面轮廓的自动化精密测量，并对精密测量进行了检验和比较分析。李剑等[4]分别对自由曲面测量中曲面CAD模型已知时测点的自适应分布、测量路径优化、自由曲面形状误差评定和CAD模型未知时的测量规划和测点数据处理等几个关键问题的实现方法进行了分析研究。结合当前数字化测量研究现状，研究并实现了大型定子叶片铸件的数字化测量及误差评定。

1 定子叶片的数字化测量

大型定子叶片铸件结构如图1所示，其中图(a)和图(b)分别为定子叶片的前视图和后视图。该铸件具有空间大曲率翼型结构，为水力学部件中一个重要的过流部件；其生产质量将影响着整个过流系统的过流效率。对大型定子叶片铸件测量的目的是为了检验实际工件的铸造工艺质量，对铸造工序所产生的型面误差进行分析和评定；因此铸造误差的测量是检验大型定子叶片工件生产质量的一项重要的测量任务，同时还可以为大型定子叶片的后续加工工序提供重要的参数依据。

针对这种大型工件的数字化测量，传统的接触式测量方法很难满足测量要求，必须采取非接触式测量；而在最常采用的非接触式测量中主要有电子经纬仪、全站仪及激光跟踪仪等三维工业测量系统。在众多的非接触式数字化测量系统中，激光跟踪测量系统以其高精度、高效率和灵活性等优点在对大型工件的测量中得到了广泛应用。为了实现大型定子叶片铸件的数字化测量，因此采用激光跟踪测量系统对工件进行测量。

大型定子叶片为自由曲面空腔类零件，结构复杂有多个曲面组合而成；测量时，激光跟踪仪一次测量很难获取大型定子叶片铸件的全部信息，为了使测量快速简便易行，需要进行转站测量[5-8]。转站测量的原理是通过改变激光跟踪仪的位置从不同测站进行测量，每次移动激光跟踪仪时需要测量若干基准点坐标，将不同坐标系下的基准点坐标对齐，就可以将测量结果统一在同一坐标系下。

不同坐标系下基准点的矢量坐标变换原理如图2所示，设空间一个基准点P在转站前测站Ⅰ坐标系里在转站后测站Ⅱ坐标系里的坐标分别为，则基准点P在坐标系σ1和σ2里的矢量依次为：

图1 大型定子叶片铸件结构

设σ2的坐标原点 o2在σ1里的坐标为(x0,y0,z0)，则o2点在σ1中的矢量为：

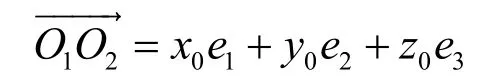
在测站Ⅰ坐标系σ1的矢量可表示为：

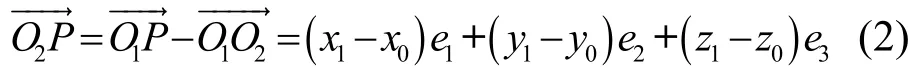
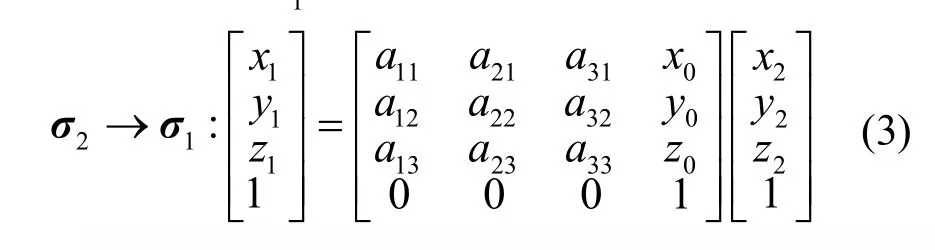
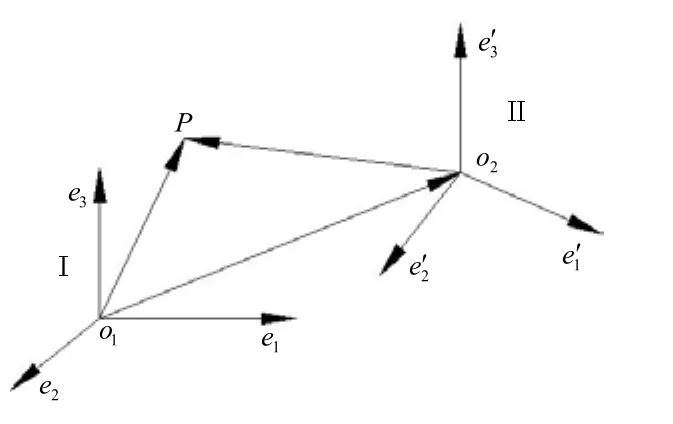
图2 不同坐标系下基准点的矢量坐标变换原理

其中元素 aij（i= 1 ,2,3;j = 1,2,3）是坐标系σ2中序号为 i的底矢 ( e1′,e2′,e3′)与坐标系σ1中序号为 j的底矢 ( e1,e2,e3)之间的夹角的余弦，如

同理，由矢量变换式(3)可将各相应测站中不同坐标系下基准点的矢量坐标对齐到测站Ⅰ坐标系下。

为了提高转站精度，采用多个空间分布的基准点转站方法，如图3所示，测得5个基准点的坐标值、对应坐标变换值及相应偏差值。通过采用5个基准点的转站测量方法实现了对大型定子叶片铸件的数字化测量，获取了大型定子叶片铸件完整的点云数据信息。

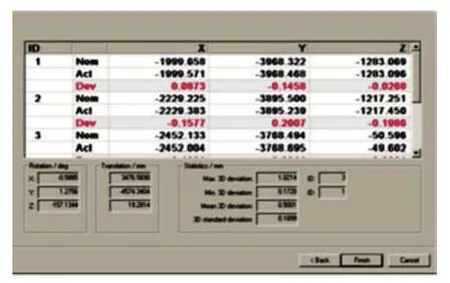
图3 5个基准点的坐标变换值及相应偏差

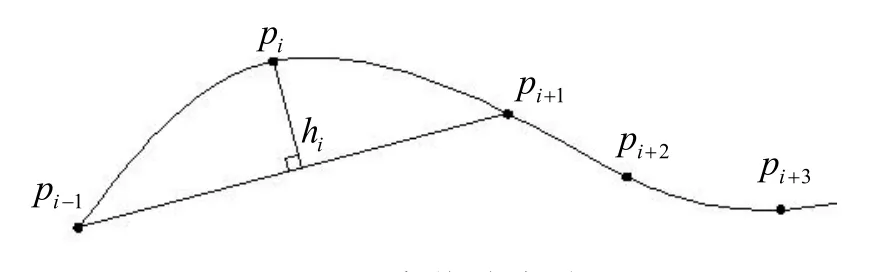
图4 弦高偏差法原理

2 测量数据处理

利用激光跟踪测量系统对大型定子叶片铸件通过转站测量方法得到了海量高密度的点云数据，在测量过程中由于测量工况、被测工件表面质量等因素的影响，容易产生一些噪声点和冗余点，这些点都是测量误差点，将影响后续点云匹配效率和误差评定质量；另外，在误差评定时过密的数据点云将会增大计算量和占用大量的计算机资源。因此，在误差评定中初始测量点云的噪声去除[1,9]和精简[10]是测量数据处理的重要工作之一。

噪声点是测量数据的误差点，对噪声点的判别常采用如下方法：①对一些明显的异常点和散乱点，可通过直观判别并予以删除。②曲线判别法：通过截面数据的首末点拟合曲线，利用最小二乘法检查中间各数据点到曲线的距离是否超过允许值来判定其是否为噪声点。③角度偏差法：计算沿扫描线方向上的查询点与前后两点形成的夹角，若不在给定的角度误差限内，则该点可视为噪声点。④弦高偏差法：连接查询点的前后两点，计算查询点到连线的距离，若该距离不在给定的弦高误差限内，则视为噪声点。

测量数据的精简是在保证一定精度的前提下减少测量点云中存在的大量冗余数据。不同类型的点云可采取不同的精简方式，如散乱点云可选择随机采样、三角网格[11]和均匀网格方法[12]；多边形和扫描线点云可采用向量加权法、平均点距值法和弦高偏差等方法。大型定子叶片铸件的测量数据属于扫描线点云，故本文选取平均点距值法和弦高偏差法对测量数据点云进行精简。

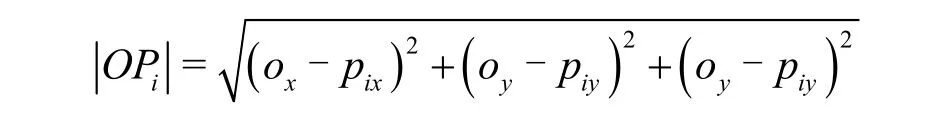
弦高偏差法：在数据点云中取一点 Pi，假设Pi（ xi,yi），连接 Pi前后两点，如图4所示，计算扫描线上点 Pi到点Pi-1与Pi+1的弦长的距离

测量数据处理结果如图5所示；图5(a)为铸件的初始测量点云，从图中可以看出某些明显的噪声点，如用于调整被测工件位置的垫块、工艺支撑立柱和支撑叶片的地面等测量工况所产生的噪声点；图5(b)为某些噪声点去除后的点云，此时点云密度较大；图5(c)、(d)为分别采用平均点距值法和弦高偏差法对测量点云的精简结果，从处理结果可以看出采用平均点距值法精简可使所有的测量点云得到了全局平均精简，无法完全体现出定子叶片的结构特征；而采用弦高偏差法精简可使在定子叶片铸件上的过渡面和圆弧面处含有较密集的数据点，而叶片型面等曲率变化不大的部分保留的数据点比较稀疏，这对后续点云匹配及误差评价工作是有利的。

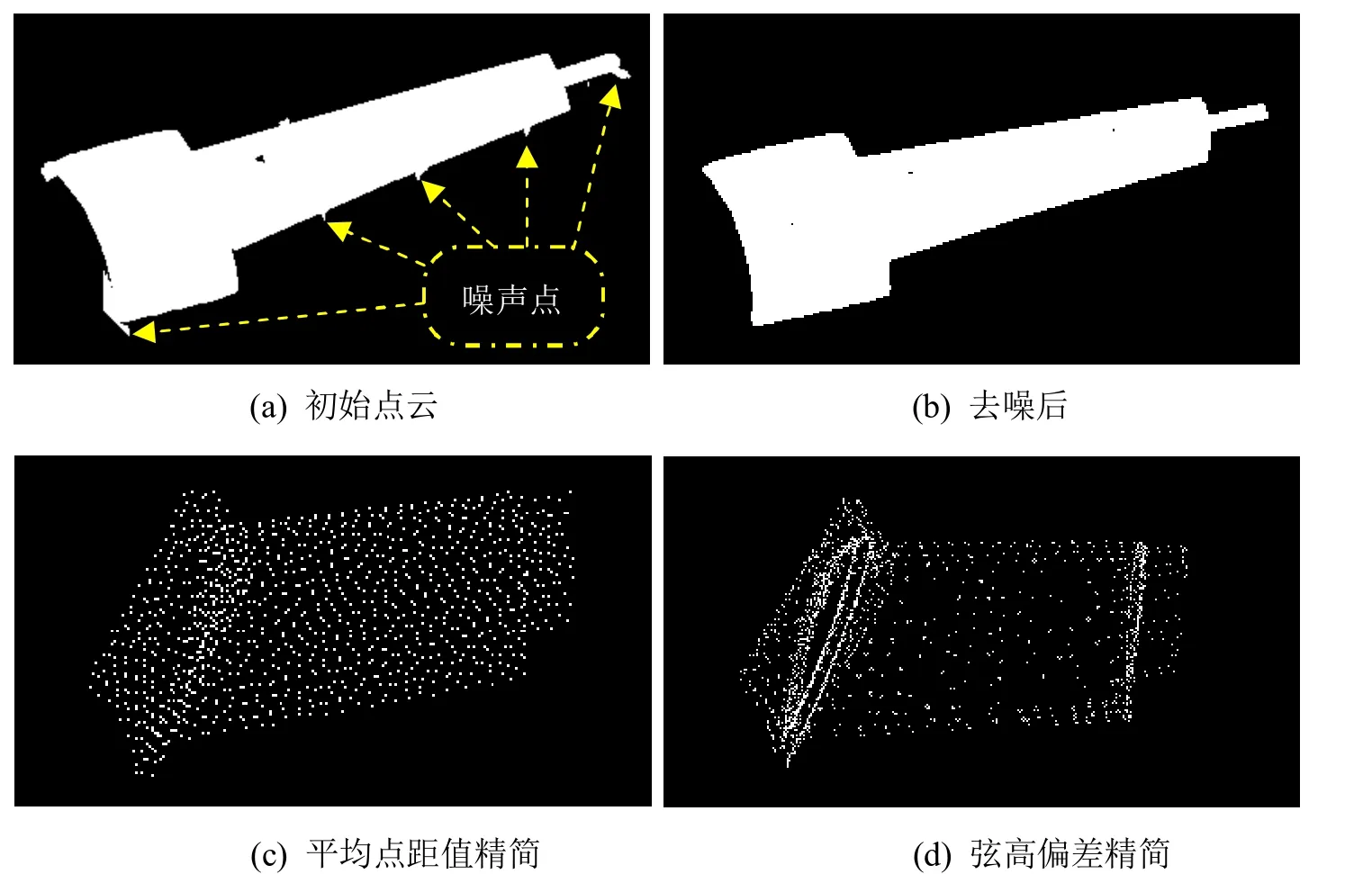
图5 测量数据点云的去噪与精简

3 基准匹配

测量数据处理完成后，在误差评定中测量点云与理论模型的基准匹配是必不可少的；由于测量坐标系和理论模型的设计坐标系不统一，在评定大型定子叶片铸件误差之前需要实现测量点云与理论模型的匹配。匹配的准则是使被测的实际轮廓点与理论轮廓面约束拟合达到最佳效果。目前较成熟的匹配方法为基于最小条件的最小区域法[13]和基于最小二乘法的最近点迭代（iterative closest point，ICP）算法[12,14]。

最小区域法以最小条件原则建立目标函数F(A)，

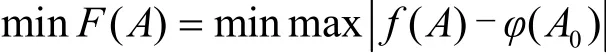
式中 f(A)为被测曲面形状误差的目标函数，φ(A0)为理论曲面的空间位置姿态函数，A和A0为曲面在空间的位置姿态，F(A)表示被测曲面经过姿态变换以后与理论曲面的最大距离函数。在对于形状规则，如直线、圆、平面等能用严格数学方程或参数表达式来表达，依照最小条件原则，比较容易建立最大最小数学模型，能够实现采用最小区域法的误差评定；而对于复杂曲面，应用最小区域法直接求解则比较困难，在工程中常采用基于最小二乘法的ICP算法等近似计算求解。

ICP算法以测量点云到理论模型的距离的平方和为目标函数F：

其中pi为数据点云中第i个测量点；qi为理论模型中的对应点即最近点；T和R分别为每个测量点pi做变换的平移向量和旋转矩阵。

使 →minF ，迭代求解刚性变换的平移向量T和旋转矩阵R，从而确定了基于最小二乘法的匹配曲面；然后求测量点到理论模型的实际距离即实际曲面的轮廓度误差。

为此将测量点云与理论模型先进行初始匹配，以理论模型的坐标系为基准，将测量点云进行旋转和平移坐标变换，使测量点云与理论模型相对位置大致吻合；初始匹配即能够缩小测量点云与理论模型之间的旋转和平移错位，又可以提高精确配准的效率和趋向。完成初始匹配之后，再采用ICP算法进行精确匹配。如图6所示，图6(a)、(b)分别为测量点云与理论模型的初始相对位置和二者精确匹配完成后的结果。

4 误差评定

利用转站测量的方法采集到大型定子叶片铸件的点云数据，对测量点云进行了去噪和精简处理，随后进行了测量点云与理论模型的基准匹配，最后计算点云到理论模型的距离，得出大型定子叶片铸件各部位的误差分布与评定结果。其结果如图7所示和部分误差数据见图8，从评定结果可知，该误差分布在-0.2932～0.7304之间；其中 85.36%的点分布在-0.0373～0.4745误差范围内，这些点分布在叶片曲面曲率变化不大的部位；而 5.56%的点分布在 0.4745～0.7304误差范围内，该点大都分布在叶片曲面曲率变化较大的部位；而9.08%的点分布在-0.2932～-0.0373误差范围内，该点大都分布在叶片内腔曲面曲率变化较大的部位及叶片铸件棱边部位。通过分析得出该定子叶片铸件的实际总体误差波动不大，偏（极）大和偏（极）小值误差主要产生于曲率变化较大的部位。

图6 测量点云与理论模型的基准匹配

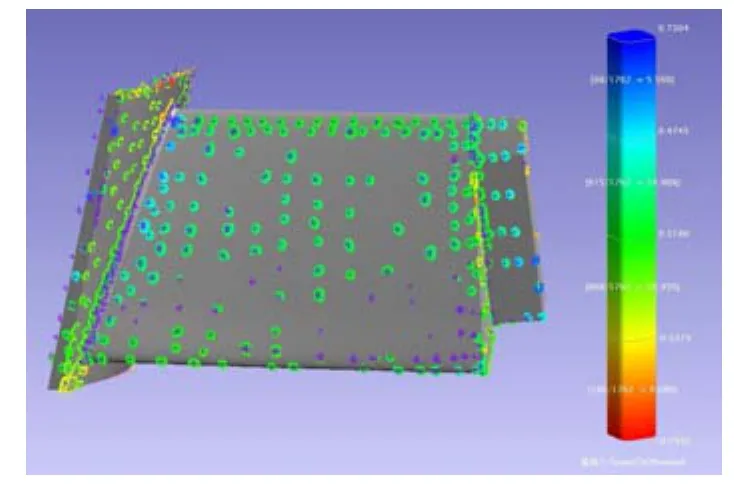
图7 大型定子叶片铸件的误差评定结果

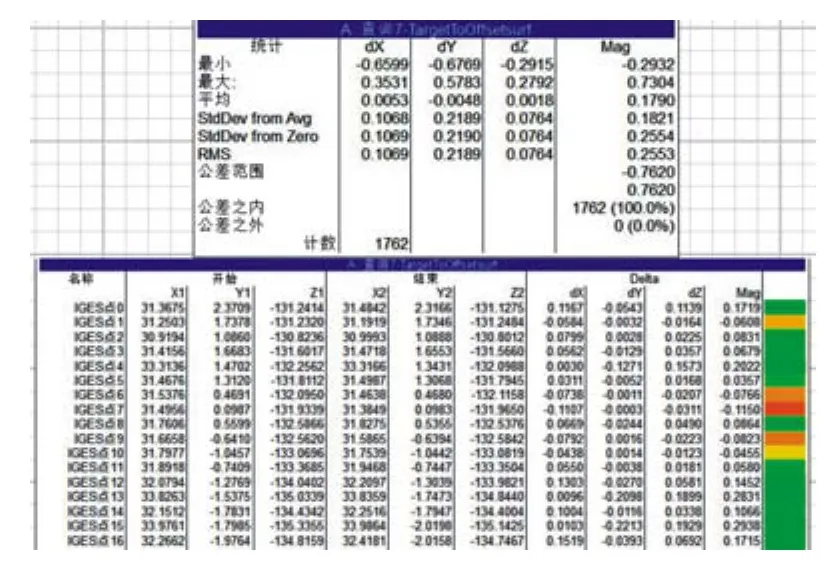
图8 误差评定报告部分数据

5 结 论

本文采用转站测量的方法完成了大型定子叶片铸件的全方位数字化测量，对海量的测量点云数据进行了去噪和精简处理，将精简后的点云数据与叶片的三维数字化设计模型进行了精确的基准匹配，计算出了点云中各点到理论模型的误差距离，得出了大型定子叶片铸件各部位的误差分布与评定结果。测量及误差分析结果应用在叶片的后续加工，优化了叶片的装夹姿态，使叶片各部位的加工余量趋于均匀，有效提高了产品制造精度和加工效率。

[1] 刘 宏,陶有丽,付家武. 自由曲面扫描线测量点云数据处理技术[J]. 组合机床与自动化加工技术,2011,(5): 77-80.

[2] 姚运萍,卢允娥. 复杂曲面数字化测量方法的研究[J]. 机械工程师,2007,(11): 59-60.

[3] Menq C H,Yau H T,Lai G Y. Automated precision measurement of surface profile in CAD-directed inspection [J]. IEEE Transactions on Robotics and Automation,1992,8(2): 268-278.

[4] 李 剑,王 文,陈子辰. 自由曲面测量若干关键问题的研究[J]. 机械科学与技术,2001,20(5): 764-766.

[5] 高瑀含,安志勇,王劲松,于秋水. 三维面型精密测量技术[J]. 红外与激光工程,2011,40(11):2261-2264.

[6] 赵幸福,田一明,杨 恢,李 伟,梁 爽,李 明. 测量不确定度评价方法在大型工件现场加工中的应用[J].组合机床与自动化加工技术,2011,(8):68-71,75.

[7] 潘国荣,张 鹏,孔 宁. 造船精度控制系统中用移站测量获取点位信息的一种方法[J]. 大地测量与地球动力学,2010,30(5): 121-124.

[8] 仝志民,唐文彦,张春富,吕景亮,张雪原. 电子经纬仪测量大型圆柱构件同轴度转站新方法[J]. 测控技术,2008,27(9): 72-74.

[9] 王格芳,吴国庆,沙晓光,吕艳梅. 激光测量的自由曲面点云数据处理方法[J]. 工程图学学报,2008,29(5): 33-37.

[10] 范 然,金小刚. 大规模点云选择及精简[J]. 图学学报,2013,34(3): 12-19.

[11] 郑惠江,何改云,丁伯慧. 离散数据环境下复杂曲面检测点布局策略研究[J]. 机械工程学报,2011,47(24): 8-14.

[12] 黄胜利,卜 昆,程云勇,周丽敏. 涡轮叶片密集点云数据与CAD模型配准方法[J]. 中国机械工程,2011,22(14): 1699-1703.

[13] 黄 祥. 基于最小区域法的圆柱度几何误差评定[J].组合机床与自动化加工技术,2013,6(6): 27-29.

[14] 徐亮胜,高 健,陈岳坪,陈 新. 复杂曲面测量数据的位姿配准方法[J]. 机械设计与研究,2011,27(4): 54-56.