一种改进的蚁群算法在工艺规划与车间调度集成优化中的应用
2014-07-09王进峰范孝良宗鹏程万书亭
王进峰, 范孝良, 宗鹏程, 万书亭
(华北电力大学能源动力与机械工程学院,河北 保定 071003)
工艺规划与车间调度(integrated process planning and scheduling,IPPS)是制造过程中的两个重要子系统。在传统制造模式下,工艺规划和车间调度往往是独立运行,互不干涉,科研工作者也往往将二者割裂研究。但是,车间生产的实际情况表明,工艺规划是车间调度的基础,将车间调度和工艺规划集成研究更符合生产的实际情况。IPPS集成研究是通过综合考虑工艺规划和车间调度来优化生产过程,将各个加工订单分解为可调整的工艺路线,并以此作为车间生产调度的输入,按照生产资源和生产系统的现状选择合适的加工工序和工艺路线,安排各加工工序在相应的机床加工,最终获得满足生产实际情况的工艺和调度方案。Chryssolouris等[1]在80年代中期第一次提出了工艺规划与车间调度集成的构想,此后科研工作者尝试使用各种方法求解 IPPS问题。Morad和Zalzala[2]第一次提出采用基于遗传算法(genetic algorithm,GA)解决工艺规划和调度集成问题。Kumar等[3]第一次试图应用蚁群算法解决工艺规划和调度集成问题。Kim等[4]采用一种共生进化算法提高了算法的搜索效率,并且在论文中设计了较为复杂的 IPPS标准算例。董朝阳和孙树栋[5]采用免疫遗传算法求解工艺设计与调度集成问题。Leung等[6]提出了基于AND/OR图的工艺规划和调度集成模型,以最小完工时间为优化目标,求解工艺规划和调度问题的方法。Wong等[7]在文献[6]的基础上,改进了蚁群算法,通过两个阶段的蚁群算法求解工艺规划和调度问题,即:工序选择和工序排序两个阶段。到目前为止,国内外的学者在解决 IPPS问题时,主要存在两方面问题:①IPPS问题的表达方案缺少柔性,往往不能反应现场的真实情况;②大部分解决方法属于单目标优化,以最大完工时间Cmax作为目标,忽视了其他更加贴合生产的实际需求,譬如交货期等。为了解决上述问题,本文改进了 IPPS问题的表达方案,为工序离散图中的工序节点增加了可选机床及其加工时间。针对蚁群算法容易出现的收敛过慢和局部收敛问题,采用信息素动态更新策略,并将多目标优化策略应用于求解过程。
1 基于AND/OR图的工艺规划与车间调度集成问题
工艺规划和调度集成问题的描述如下:
m 台机床{W1,W2,…Wm}完成 n个零件{J1,J2,…Jn}的加工。每个零件 Ji包含 p道工序{Oi1,Oi2,…Oip},可形成由p道工序按照一定规则构成的q道可选工艺路线{Li1,Li2,…Liq},集成问题的优化目标是确定n个零件的工序,并根据工厂的实际情况,进行车间作业调度。IPPS问题描述,还需要引入以下条件:
(1)完成工序 Oij的机床 Wk可选,某道工序指定机床的加工时间tijk已知,其中{Oij∈O,Wk∈W,i = 1,2,…,n,j = 1,2,…,p ,k = 1,2,…,m};
(2)某个时刻每台机床Wk只能处理一个作业Ji,同一作业Ji的两道工序不能同时加工,且工序Oij一经开始就不能中断;
(3)机器调整时间和零件运输时间忽略不记;
(4)不考虑机床故障等突发性因素。
为了便于应用蚁群算法解决 IPPS问题,将IPPS问题表示为AND/OR图,AND/OR图是一个由3种元素构成的离散图,即节点集、有向弧/无向弧集、AND/OR关系。节点集代表所有零件工艺路线包含的所有工序 Oij。有向弧表示同一零件加工工序间的优先级关系。无向弧表示蚂蚁在不同零件工序间可能存在的访问关系。有向弧和无向弧表示蚂蚁从一个节点到另一个节点可能走的路径。节点、有向弧、无向弧构成所有零件的可行工艺路线。图1为两个零件的离散工序图,节点O12代表零件1的第2道工序。工序O12可由两条台机床加工W4,W6,其加工时间分别为9 s,8 s。图1中零件2的节点工序O21包含7条无向弧,分别指向零件1的7道工序。同理,零件1和零件2的每个节点工序都包含若干指向其他节点的无向弧。为了使图1不过分凌乱,图中只表示了工序O21的无向弧,而忽略了零件1和零件2的其他节点工序的无向弧。
同一零件的不同工序之间除了优先级关系外,还有AND、OR关系。AND关系指的是工序间的串行关系,而OR关系指的是工序间的并行关系。图 1中“AND-1”关系表示的是工序O15、O16允许出现两种排列,即 O15->O16和O16->O15,图1中“OR-2”关系表示工序O22之后,可以是工序O23,也可以是工序O26和O27。因此,图1所示AND/OR图中表示的零件1和零件2的工艺路线如表1所示。
2 应用蚁群算法解决IPPS问题
本文针对IPPS问题的复杂性,在文献[7]的基础上,改进了 IPPS问题的表达方案,应用了多目标优化策略改善 IPPS问题的求解质量,为了避免收敛过慢和局部收敛问题,采用信息素动态更新策略。
2.1 工序选择阶段
该阶段 AND/OR图中的节点是信息素的携带者。蚁群中的所有蚂蚁置于开始节点,蚂蚁按照一定的选择概率选择下一节点,该选择概率取决于两方面,即下一节点的能见度ηuv和蚂蚁遗留在节点的信息素τuv,因此,蚂蚁r选择下一节点的概率可表示为:节点u到节点v遗留在节点v的信息素,β为能见度的权重系数,α为信息素的权重系数。aces[r]为蚂蚁r在节点u的下一节点访问列表。

图1 两个零件的工序离散图

表1 零件1和零件2的工艺路线
下一节点的能见度主要取决于该节点工序在相应机床的加工时间。通常情况下,节点工序加工时间越短,蚂蚁选择该节点的概率越大。因此,节点v的能见度如式(2)所示。

式(2)中tijk为工序Oij在机床Wk的加工时间,E为能见度影响系数,为正值,其取值大小取决于tijk,从式(2)可看出,节点v的能见度与tijk成反比,tijk越小,蚂蚁选择该节点的概率越高。
蚂蚁在每次寻优过程中,在其访问节点中都会堆积信息素,该信息素随着时间历程会逐渐消退。最终堆积在各个节点的信息素将引导蚂蚁选择相应的节点,当蚂蚁初始迭代前,各节点设定信息素初值0τ。各个节点采用动态的信息素更新

式(1)中u为源节点,v为目标节点,ηuv为从源节点u到目标节点v的能见度,τuv为蚂蚁r从策略,该策略主要包括全局更新和局部更新两种策略。
2.1.1 全局更新
对于蚂蚁 r,每完成一次从开始节点到结束节点的迭代,则更新途径路径中每个节点的信息素。各个节点信息素τuv如式(3)所示:

式(3)中τuv(new)为蚂蚁r迭代后堆积在节点v上的信息素,ρglobal为信息素挥发系数,ρglobal=ρ0,τuv(old)为蚂蚁r迭代前节点v上的信息素,Δτr为蚂蚁r本次迭代结束后,节点v的信息素增量。其中,该增量大小与蚂蚁r完成本次迭代后的时间历程有关。因此,节点v的信息素增量Δτr如式(4)所示:

式(4)中Qglobal为信息素增量系数,Qglobal=Q0。Ck为蚂蚁r完成本次迭代后的时间历程,其取值可由式(5)计算:

式(5)中Xijk:调整系数,其值为:

2.1.2 局部更新
局部更新策略主要为了解决两种情况,即收敛过慢和局部收敛。
(1)局部更新策略一。为了加速蚁群算法的收敛,对于表现较好的节点可加速其信息素的堆积。因此,对于单次迭代表现最好的蚂蚁所选择的节点再次执行信息素更新操作。即:当某次迭代中,蚁群中所有的蚂蚁完成遍历后,选择 Cr最小的访问路径的各个节点,再次执行信息素的更新操作,其更新公式如式(3)~(6)所示,这种方法能够加速信息素在较优路径上的堆积,从而提高了算法的搜索效率。
(2)局部更新策略二。局部收敛指的是当连续几代蚁群搜索的最优路径完全相同,并且该解明显不是最优解时,则蚁群算法陷入了局部收敛。导致产生局部收敛现象的直接原因是信息素的非正常快速堆积。为了判断是否存在局部收敛,设置局部收敛判断指标StdRpt。当蚁群算法执行过程中,连续NumRpt代蚁群输出相同的最优节点列表时,则系统判断存在局部收敛,系统启动信息素局部更新策略。局部更新策略主要包括调整信息素的挥发速度和减弱局部较优路径的信息素量。因此,式(3)变更为:
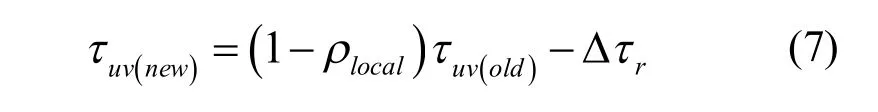
式(7)中

信息素增量Δrτ如式(9)所示:

式(8)中

Cr取值同式(5)和式(6)。
当蚁群中的蚂蚁经过多次迭代后,AND/OR图中相应的访问节点则堆积了一定的信息素,最终在AND/OR图中形成一条相对固定的路径,该路径包含了每一个零件的某一道可行工艺路线的所有节点,该节点列表即为工序选择阶段的输出,也是第二阶段工序排序阶段的输入。
2.2 工序排序阶段
本阶段对第一阶段形成的节点列表进行工序排序,蚁群置于开始节点,算法执行,完成从开始节点到结束节点的遍历。本阶段节点间的有向弧和无向弧成为信息素的携带者。蚂蚁选择节点及弧段时的选择机制同第一阶段,但是由于本阶段最终要形成合理的调度方案,因此,其评价指标不同于第一阶段。通常情况下,调度方案的评价指标根据优化目标不同而不同。本文将最大完工时间Cmax最小化、最大负荷机床负荷Lmax最小化和车间机床最大负荷差值最小化Bmax作为优化目标。
最大负荷机床负荷Lmax可表示为:
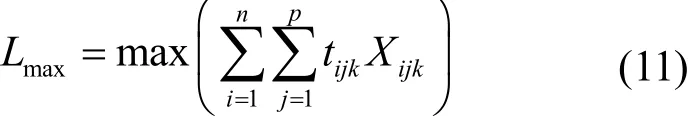
其中:Xijk如式(6)所示。
机床最大负荷差值Bmax可表示为:

式(12)中Lmin是最小负荷机床负荷。
最大完工时间Cmax可表示为:

式(13)中Ci是零件Ji的完工时间。
为了简化优化过程,根据上述3个优化目标的重要程度,分别为之设置不同的权重系数,则多目标优化问题转变为单目标的优化问题。式(4)和式(9)中的Cr可以表示为:

式(14)中,Cmax(r)、Lmax(r)、Bmax(r)表示蚂蚁r完成某次迭代后的最大完工时间,最大负荷机床的负荷,车间机床最大负荷差值。λC、λL、λB分别表示Cmax(r)、Lmax(r)、Bmax(r)的权重。
本阶段各弧段的信息素更新也需要全局更新和局部更新相结合的信息素动态更新策略。
3 算例仿真
以图1所示的IPPS问题为例,验证算法的有效性。设定初始参数如下:K=8,MaxRpt =5,τ0=1.0,ρ0=0.65,E=20,Q0=100,α=2.0,β=1.0。经过上述算法后,形成了输出节点列表,原AND/OR图则转变为图2所示的AND/OR图。

图2 工序选择后的AND/OR图
在图2所示的AND/OR图中,应用上述第二阶段蚁群算法,进行路径寻优。设定初始参数如下:K=8,MaxRpt=5,τ0=1.0,ρ0=0.65,E=10,Q0=100,α=2.0,β=1.0,λC= 0.3、λL= 0.2、λB= 0.5。获得的最优路径,如图3所示。
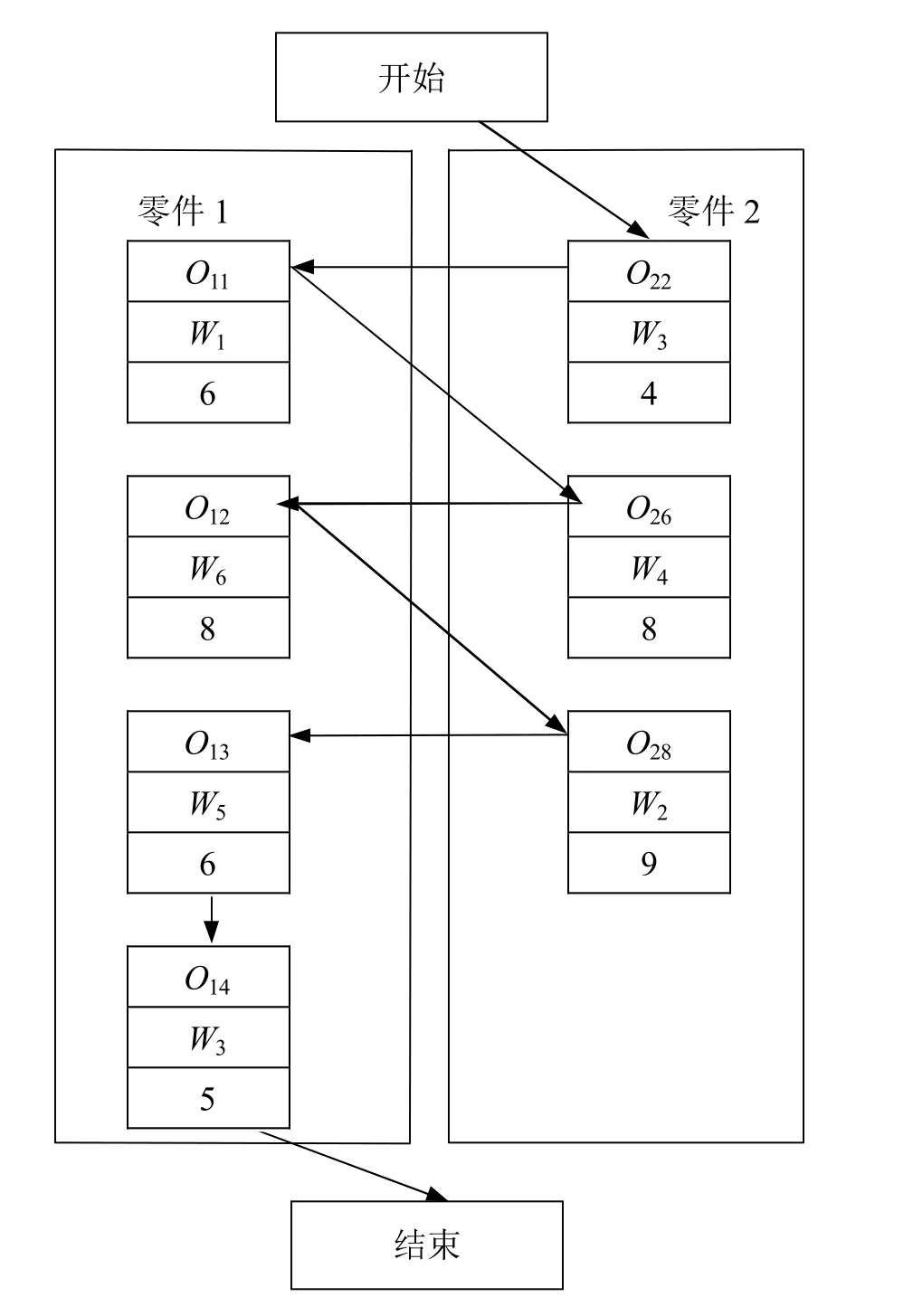
图3 最优路径
为了进一步验证算法的有效性,以韩国学者Kim在2003年提出的标准算例进行测试。该标准算例由18种零件组成,每种零件由8~22道工序组成,由18种零件组成了24个测试问题,具体的标准算例数据见参考文献[8]。对比 Kim[8]的SEA算法[4]和本文提出的改进ACO算法的最大完工时间Cmax,结果如表2所示。
从表2的数据,可以发现大部分测试算例的Cmax都有改进,算例10的Cmax改进程度达到了24%,算例13、15、19、21的改进程度也超过了10%。但是对于个别算例,譬如,算例18的Cmax不仅没有改进反而有所降低,反复测试该算例,发现,本算法在解决此算例问题时,反复的陷入局部收敛或者接近局部收敛,需要对局部更新策略重新设计。
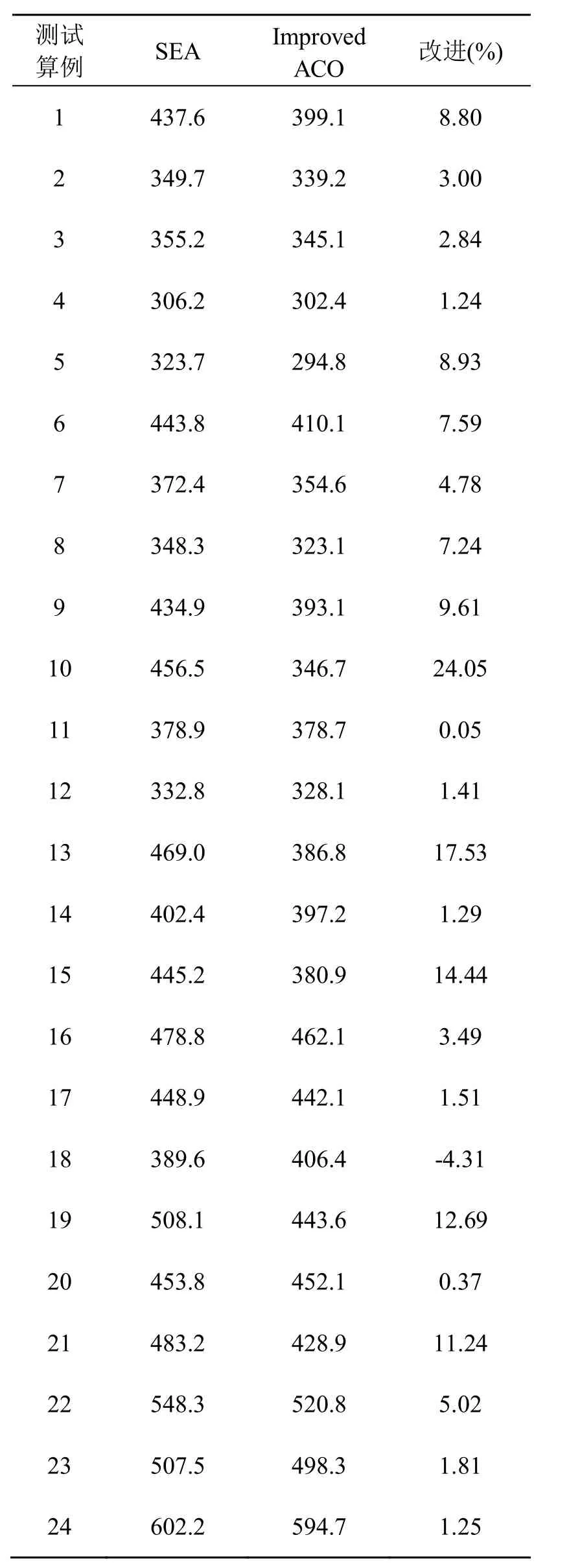
表2 对比测试结果
4 结 束 语
本文改进了标准蚁群算法求解 IPPS问题的策略。通过节点集、有向弧/无向弧集、AND/OR关系,优化了 IPPS问题的求解模型,采用局部更新策略一,加速信息素的堆积,提高了算法的搜索速度;采用局部更新策略二,避免了算法的局部收敛。在工序排序阶段,应用多目标优化策略,提高算法的求解质量。针对具体实例进行了仿真试验,给出了各个参数的最优取值和最终的仿真结果。
[1] Chryssolouris G,Chan S,Cobb W. Decision making on the factory floor: an integrated approach to process planning and scheduling [J]. Robotics and Computer-Integrated Manufacturing,1984,1(3~4):315-319.
[2] Morad N,Zalzala A. Genetic algorithms in integrated process planning and scheduling [J]. Journal of Intelligent Manufacturing,1999,10(2): 169-179.
[3] Kumar R,Tiwari M K,Shankar R. Scheduling of flexible manufacturing systems: an ant colony optimization approach [J]. Proceedings of the Institution of Mechanical Engineers,Part B: Journal of Engineering Manufacture,2003,217(10): 1443-1453.
[4] Kim Y K,Park K,Ko J. A symbiotic evolutionary algorithm for the integration of process planning and job shop scheduling [J]. Computers & Operations Research,2003,30(8),1151-1171.
[5] 董朝阳,孙树栋. 基于免疫遗传算法的工艺设计与调度集成[J]. 计算机集成制造系统,2006,12(11):1807-1813.
[6] Leung C W,Wong T N,Mak K L,Fung R Y K.Integrated process planning and scheduling by an agent-based ant colony optimization [J]. Computers and Industrial Engineering,2010,59(1):166-180.
[7] Wong T N,Zhang Sicheng,Wang Gong,Zhang luping.Integrated process planning and scheduling-multiagent system with two-stage ant colony optimization algorithm [J]. International Journal of Production Research,2012,50(21): 6188-6201.
[8] Kim Y K. 2003[EB/OL]. [2013-06] http://syslab.chonnam. ac.kr/links/data-pp&s.doc.
