基于面部曲线弹性匹配的三维人脸识别方法

潘仁林， 达飞鹏， 邹红艳， 王朝阳

（东南大学自动化学院，江苏 南京 210096）

与指纹识别、虹膜识别等生物特征识别技术相比，人脸识别具有非接触、隐蔽性好等特性，而成为当前模式识别和计算机视觉领域的研究热点。传统的基于二维灰度或彩色图像的二维人脸识别已获得较好的识别性能，但仍易受光照、姿态、表情等因素的影响，其本质原因在于图像是三维物体在二维空间的简约投影。三维人脸数据包含比二维人脸更多的信息，且不会受姿势和光照的影响，所以基于三维人脸数据的三维人脸识别具有更好的识别效果[1]，近些年受到越来越多的关注。目前三维人脸识别已广泛应用在门禁系统、机场安检、视频监控、智能空间、自然人机交互等领域，如A4Vision公司为丹佛地区公共运输系统(the regional transportation district，RTD)装备 RFID 3D脸部识别门禁系统，该系统利用RFID卡和A4Vision公司领先的3D脸部识别器为丹佛地区公共运输系统的财政部提供更高一级的安全保证。

目前有关三维人脸识别方法的研究有很多，根据特征形式可以分为基于空域直接匹配、基于整体特征匹配和基于局部特征匹配的三维人脸识别方法。基于空域直接匹配的方法不提取特征，而是直接进行曲面的相似度匹配，常用的方法有迭代最近点法(iterative closest point,ICP)[2]和Hausdorff距离法[3]等。这类方法在匹配刚性曲面时具有较好的效果，但是由于人脸曲面本质上是一个非刚性曲面，易受表情变化的影响，因而研究人员提出对刚性区域进行ICP匹配的解决方案。基于整体特征匹配的方法注重三维人脸的整体特征，如基于深度图的表观匹配方法[4]将人脸曲面映射为二维人脸深度图，然后对深度图进行主元成分分析(principal component analysis，PCA)匹配；基于 EGI[5]的人脸匹配方法将曲面转换为单位球面上的质量分布映射图(extended gaussian image，EGI)，然后匹配 EGI。基于局部特征匹配的方法主要是提取人脸曲面上的局部特征进行匹配。常用的三维人脸识别的局部特征包含局部描述符[6]、曲线特征以及其他一些局部的几何特征和统计特性。

一些研究人员在三维人脸曲面上提取表征人脸几何信息的特征曲线，将人脸曲面的匹配转化为曲线的匹配，极大提高了匹配的效率。Beumier和 Acheroy[7]提取经过人脸曲面上最突出点的中心轮廓线和两条平行于该线的轮廓线，通过比较选定轮廓线上的各点的曲率值得到三条轮廓线相似度，进一步融合得到人脸曲面的相似度。但该方法只提取三条人脸曲线，丢失很多曲面信息，表征性较小，当库集人脸个数较多时识别率会下降。Samir等[8]在人脸深度图上提取等深度轮廓线，然后计算测试人脸等深度轮廓线与库集人脸相应的等深度轮廓线在黎曼空间上的测地距离作为匹配相似度。文献[9]提取多条等测地线来表征人脸曲面，计算曲面上的等测地线与另一曲面上的等测地线的黎曼空间测地距离作为匹配相似度。Berretti等[10]没有使用等测地线，而是根据曲面点到鼻尖的测地距离将人脸划分为若干个等测地区域，然后根据对应等测地区域上的点之间的位置关系来识别人脸。Gokberk等[11]提取人脸面部上的七条垂直轮廓曲线，计算每条对应曲线之间的相似度然后融合为最后的总相似度来识别人脸。Chao等[12]利用三维人脸模型的轮廓线和等高线进行识别，结果表明将中心垂直侧面轮廓线和等高线的相似度融合起来得到的识别率高于任一种曲线单独使用得到的识别率。

从上面介绍的各种基于曲线匹配的三维人脸识别算法中很容易看出基于曲线的识别方法分为两个方面即表征人脸的曲线类型和曲线匹配的方法的选择。

本文受二维分层匹配思想[13]的启发，提出了一种基于面部径向曲线弹性匹配的三维人脸识别方法。首先，对三维人脸进行预处理，提取从鼻尖点发射的多条面部径向曲线，并对径向曲线进行重采样后提取有用点以建立曲线之间的点对应关系；然后，对测试人脸的每条径向曲线与库集人脸的对应曲线进行分层弹性匹配，再根据测试人脸与库集人脸建立的点对应关系，利用对应点到鼻尖点的距离匹配曲线；最后，将每条曲线的两种匹配相似度进行加权融合作为总相似度用于识别。人脸识别过程框架如图1所示。测试结果表明，本文方法具有很好的识别性能，并且对表情、遮挡和噪声具有较好的鲁棒性。

1 三维人脸预处理

本文实验采用 FRGC v2.0数据库的三维人脸模型，主要为三维点云格式。每个三维点云由80 000～130 000个点构成，包含了人脸区域，以及耳朵、头发和肩膀等冗余区域，因此需要对人脸模型进行必要的预处理（图2(a)），以减少噪声干扰，提高识别率。

1.1 鼻尖点的确定及区域切割

为了去除耳朵、头发和肩膀等冗余区域，准确提取人脸区域，首先需要确定鼻尖点的位置。本文参照文献[14]的方法根据人脸形状指数(Shape Index)特征确定鼻尖点候选区域，然后和标准模板人脸进行ICP匹配以确定鼻尖点位置，最后根据该鼻尖点位置切割人脸区域。

人脸形状指数(shape index)特征由 Dorai和Jain[15]提出，表示三维曲面上每一点邻域的凹凸程度，并与坐标系独立。点p的Shape Index值可由它的最大主曲率k1(p)和最小主曲率k2(p)得到：

图1 人脸识别系统框架

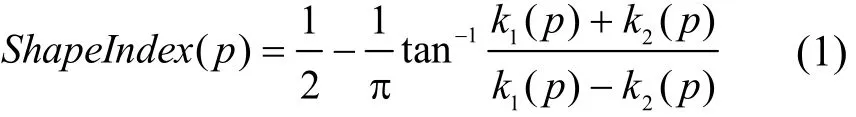
鼻尖在人脸中是一个最突起的区域。首先，根据式(1) 计算点云中每一点的Shape Index值，选取 Shape Index值在一定范围(0.85～1.00)内的点组成的区域作为初始鼻尖候选区域；然后，选定一个标准模板人脸，并手动定位其鼻尖点；最后，将上述三维人脸模型与标准模板人脸进行ICP对齐，在三维人脸模型的鼻尖点候选区域中选择与标准模板人脸的鼻尖点相对应的点作为鼻尖点。以鼻尖点为中心，以半径r=90 mm做球体，球体内包含的人脸区域即为切割的人脸区域。

1.2 三维人脸点云平滑去噪

由于采集设备、环境和目标的影响，原始三维点云会包含一定的噪声信息。如眼睛、鼻孔等区域的反射率变化会导致三维人脸模型的相应位置出现离群点；使用激光采集时，在眉毛、胡须、遮挡或者嘴巴张开等光线暗淡区域由于无法采集到点云数据会产生人脸点云上的孔洞等。这些噪声将严重影响人脸识别率，因而必须对这些噪声进行处理，以去除噪声对识别效果的影响。首先，将人脸区域的三维点云网格化；然后，采用高斯平滑滤波器去除人脸网格上的高频信息从而消除人脸模型上的尖点；最后，通过对有效邻域的线性插值达到填补孔洞的效果。三维人脸点云平滑去噪后的效果如图2(b)所示，平滑之后将人脸恢复成点云格式。

1.3 人脸姿态校正

对平滑去噪后的人脸区域点云进行主元成分分析(PCA)，可得到3个互相垂直的主方向，将最大特征值对应的特征向量作为新坐标系的y轴，最小特征值对应的特征向量作为z轴，建立右手坐标系，该坐标系也被称为姿势坐标系(pose coordinate system，PCS)。以鼻尖点作为该坐标系的坐标原点，将切割后的人脸区域点云转换到 PCS中，得到具有正面姿态的三维人脸数据，校正后的人脸如图2(c)所示。

图2 人脸预处理

2 人脸径向曲线提取及重采样

三维人脸的曲线特征不仅能够表征人脸曲面的几何信息，而且能够减少三维人脸模型的数据量，提高匹配效率。人脸径向曲线相比于测地线，等深度曲线等人脸面部曲线具有提取简单、反映面部凹凸程度显著等优点，因而本节提取从鼻尖点发射的多条面部径向曲线作为三维人脸的识别特征。

2.1 三维人脸径向曲线的提取

在PCS中，记具有正面姿态的三维人脸曲面为S，坐标系YOZ平面的上半平面为p1，以p1切割人脸曲面，如图3(a)所示。计算人脸点云上每个点到该平面的距离，选择距离小于阈值δ=0.3的点的集合作为径向曲线c1。然后将平面p1绕Z轴以α=10°为间隔逆时针旋转为pi(i = 2 ,3,… ,3 6)，并与三维人脸曲面S相交得到径向曲线 ci(i = 2 ,3,… ,3 6)。提取的人脸径向曲线如图3(b)所示，以径向曲线的集合近似表征三维人脸曲面 S ≈ ∪ici(i = 1 ,2,… ,3 6)，不仅很好地保留了人脸大部分几何信息，而且简化了三维人脸曲面的数据量。

由于人脸点云的分布不均匀，导致提取的径向曲线 ci(i = 1 ,2,… ,3 6)上的点密集程度不一致，因此需要对其进行重采样。将径向曲线近似为切割平面pi上的二维曲线，选择pi与XOY平面相交的直线作为参考曲线进行重采样，重采样过程如图3(c)所示，图中蓝色曲线为参考曲线，在参考曲线上每隔1 mm采样一个点。对于参考曲线上的每个点，选择径向曲线上与该点在参考曲线方向上的距离dis最近且小于阈值ζ=0.3的点作为径向曲线的采样点，这样就得到一条在参考曲线方向上均匀分布的径向曲线，同时对径向曲线上的点根据参考曲线方向进行了排序，并且减少了每条径向曲线上的点的个数。图3(d)上方的曲线为原始曲线，下方为重采样后的曲线。

2.2 径向曲线有用点的提取

由于遮挡和数据丢失的影响，不是每个采样参考曲线上的点都有与之对应的采样点，因而待匹配人脸的相应径向曲线通常具有不同的点数，为了组成不包含空点的采样点对，我们剔除径向曲线上的冗余点，保留有用点用于最后的识别。

对一条采样参考曲线上的任一点，使用flag标志该点位置是否包含采样点。重采样时参考曲线上每隔1 mm的对应位置上若存在采样点，则参考曲线该点位置处的标志flag设为1，否则设为0。在之后的比对中，如果测试集或库集中的参考曲线上的一点位置处的标志flag等于0，则剔除这组测试集和库集的对应采样点对。这样就在一定程度上通过选取有用点使得识别时不受遮挡和数据丢失这些因素的影响。

图3 曲线提取及重采样

3 三维人脸径向曲线的分层弹性匹配方法

基于二维形变曲线模型分层描述的分层弹性匹配算法可以捕捉模型的各个层级的几何形状信息，因而可用于形变模型的形状分析、形变模型的相似度匹配等。与传统的形变模型分析方法相比，该方法由于使用分层形变模型表征，从而具有能够在弹性匹配算法中考虑全局几何信息的优势。

在分层弹性匹配的过程中，引入形状树的概念。首先，建立库集人脸每条曲线的形状树；然后，与测试集人脸上对应的曲线进行分层弹性匹配；最后，对所有的相似度进行加权融合得到分层匹配相似度。

3.1 形状树建立

本文方法中使用开放并且经过排序的径向曲线，A表示由一系列采样点 ( a1,a2,… ,an)组成的曲线，选取A上的一点ai作为中间点，一般取表示ai相对于a1和an的位置，本文为ai相对于a1和an的Bookstein坐标[16]，即将两个首尾采样点映射至固定位置从而确定的一个坐标系下的坐标。由于首尾采样点的位置的确定，只需一个中间采样点的Bookstein坐标就能很好地表示3个点的相对位置关系。首先将a1映射至(-0.5,0)、an映射至(0.5,0)，则ai相对于a1和an的位置L(ai|a1,an)=(a(1),a(2))，(a(1),a(2))由下列公式求得

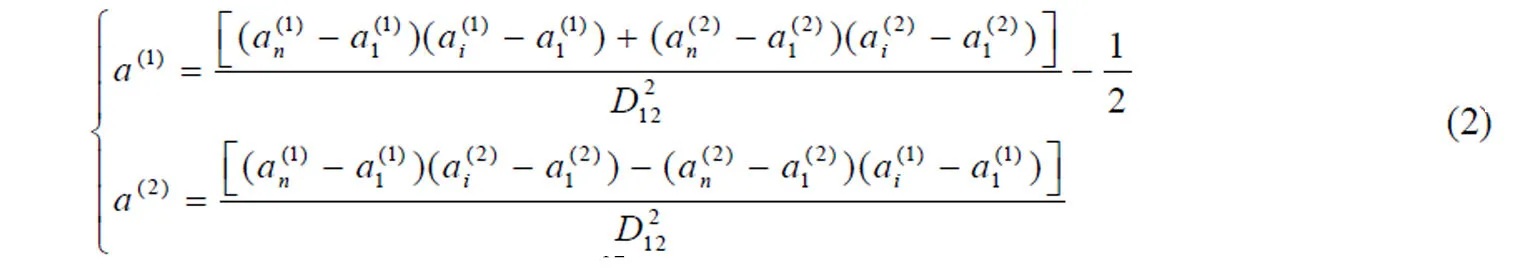
选取的中点ai将曲线A分成 A1=(a1,…,ai)和 A2=(ai,…,an)两部分。曲线A的分层描述具有递归性，即曲线A的分层描述由相对位置及 A1和A2的分层描述组成。该分层描述可以用二叉树进行表征，我们将曲线的二叉树表征称为形状树表征，如图4(b)所示。形状树的根节点描述曲线A的中间点ai相对于a1和an的位置左子结点描述 A1的中间结点与a1和ai的相对位置，右子结点描述A2的中间结点与ai和an的相对位置。对于子曲线，其中p,q为子曲线C在整个曲线中的首尾端点序号位置，选取中间点为，对应的子结点描述为L(ak|ap, aq)。依次分层描述，直到时停止分层描述，形状树建立完毕。

图4 分层匹配算法原理图

形状树上的每个结点记录该段曲线的中间点与首尾采样点的相对位置。左子结点描述首采样点到中间点的子曲线，右子结点描述从中间点到尾采样点的子曲线。叶子结点表示采样点和与它左右相邻的采样点的相对位置。容易看出以某一结点为根的子树表征该段子曲线的形状树。

形状树的底层结点表示该条曲线上连续三个点的相对位置，这些结点包含局部几何信息如中间点与相邻采样点的相对位置等。靠近形状树根结点的结点记录中间点与距它距离较远的首尾采样点之间的相对位置，因而包含更多的全局几何信息。

以a1和an为首尾采样点的曲线A，我们可以根据形状树表征递归重构该曲线。通过将初始点a1和an安放在任意位置，等价于对曲线A进行了一次平移、旋转和尺度变换。因而分层匹配算法对平移、旋转和尺度变换具有不变性。

3.2 改进的分层弹性匹配

对两条开放曲线A和B进行匹配，首先建立曲线A的形状树表征，然后在曲线B上寻找与曲线A的对应关系，使得曲线B与曲线A具有最小的形变误差。下面介绍具体的匹配过程。

对于两条待匹配曲线 A =(a1,a2,… ,an)和B=(b1 ,b2,…,bm)，设a1对应于b1，an对应于bm。A的形状树表征的中点ai将曲线A分成 A1和A2两部分。将b2, b3,…,bm-1依次作为B的中间点bj，bj将曲线B分成B1和B2两部分，分别对应 A1和A2。如果该点bj使得 A1和B1的相似度s1，A2和B2的相似度s2及两条曲线中点的相对位置L(ai|a1,an)和 L (bj|b1,bm)分配权重的相似度s3之和 s = s1+ s2+ s3最小，则该最小的相似度s作为 A和B的最终相似度，子曲线 A1和B1之间的相似度计算按A和B相似度方式计算。整个过程可以看作是一个寻优递归的过程，曲线A和B的相似度可以根据下面的寻优递归等式进行计算

其中，dif表示A和B的中间点的相对位置误差，λA为权重因子。

形状树的分层特性确保了在匹配过程中很好地考虑整体和局部几何特性。事实上，对于形状树上的不同结点我们使用不同的权重来改变形变量大小。如对形状树根部的结点，这些结点对全局几何信息影响较大，因而给予其较大的权重因子。对于本文人脸识别实验，可根据曲线的长度来确定权重因子，对于中间点与首尾采样点相对位置较远的形变量分配更高的权重因子λA，反之，则更小。

由于本文采用Bookstein坐标表示3个点的相对位置关系，该坐标系上的点被认为相当于morphospace空间[16]上的点，因而本文采用普式距离[17]计算中间点的相对位置误差，对于Bookstein坐标分别为 ( x1,y1)和 ( w1,z1)的两点，首先根据式(4)将 ( w1,z1)映射为 ( u1,v1)：

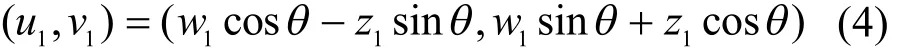
其中

然后计算普式距离为：

下面就φ(A,B)的基本情况即当A或B只有两个采样点时进行讨论。只有两个采样点的曲线相当于一条线段，当两条线段进行匹配时匹配代价为0，当一条线段与另一条可再分曲线进行匹配时，匹配代价根据可再分曲线的长度确定，可再分曲线长度越长，匹配代价越大，反之匹配代价越小。

使用动态规划方法求解式(3)，由于使用了递归思想，如果依次搜索曲线上的每个点与形状树表征的中间点对应并匹配，则计算代价非常大，为此对算法进行了改进。由于人脸曲面相当于一个三维空间中的二维黎曼流形[18]，因而人脸曲面的形变可近似用等距变换来描述，即人脸曲面发生形变时，人脸表面曲线基本没有拉伸或者收缩，除了嘴部等易发生较大形变的区域，其他区域的形变基本保持在一定的范围内，为此我们可以在这些形变曲线匹配时缩小中间点的搜索范围。可选择在一定范围内搜索从而既能大大提高时间效率，又不会对识别率产生影响。

受表情的影响，人脸曲面会发生一些形变，比如，大笑的表情就会使得嘴巴部分产生很大形变，而鼓腮的表情则使得脸颊部分产生形变，皱眉和笑的时候就会导致眼睛的形变等，而额头，鼻子等区域受表情影响较小。需对不同区域的曲线的相似度赋予不同的权重并进行加权融合。对额头区域加大权重，对嘴巴和眼睛区域减小权重。

这里的权重计算如下式表示：

其中i为径向曲线的序号，径向曲线所处的区域均为经验值。将 36条径向曲线匹配的结果进行融合，则得出的人脸分层匹配相似度为：

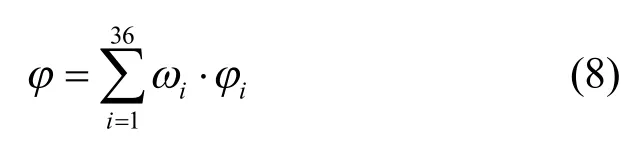
其中iφ为测试人脸第i条径向曲线与库集人脸相应的径向曲线比较所得的分层匹配相似度。通过对不同曲线分配不同权重，很好地克服了表情变化带来的影响。

3.3 点距信息融合

人脸上提取的径向曲线近似为二维曲线，因而可以采用分层匹配算法进行匹配，并取得了一定的识别效果，但由于只采用了径向曲线上采样点的二维坐标信息，丢失了部分三维空间信息，对识别率产生了一定的影响。为此需结合径向曲线的特性，对径向曲线进行有用点提取并建立人脸曲线的点对应关系，利用每个采样点到鼻尖点的欧式距离进行匹配，有效地弥补了分层匹配算法包含的曲线空间信息不足的缺点，本文将该步骤称为点距匹配，第4节的实验证明了该方法的有效性。

由于每条径向曲线的对应参考曲线上的任意一点位置处都有一个是否包含采样点的标志flag，在进行特征比较之前，首先得出对应位置处采样点是否可用的标志pflag：

即测试人脸上的点a和库集人脸上的点b，这两个相互对应的采样点均可用（flag的值都为1）时该对采样点才能参与比较。这样，假设每个人脸第i条径向曲线总共采样点数为ni时，实际所用到的采样点并不相同，只有通过式(9)的判断才能得出，这里有用的采样点对数记为Ni。设库集人脸第i条径向曲线上第j个采样点与鼻尖点的距离为 dGj，测试人脸第i条径向曲线上第j个采样点与鼻尖点的距离为 dPj，则每条径向曲线的特征相似度定义如下式：

通过式(10)求出36条径向曲线的相似度，然后根据式(11)求和得到人脸的点距相似度φ，其中iω按式(7)计算。

3.4 相似度计算

对于具有N个人脸模型的库集，将会分别得到分层匹配相似度向量和点距相似度向量为了融合两种相似度，分别对两种向量进行归一化，即：

4 实 验

实验采用FRGC v2.0数据库，FRGC v2.0数据库包含466个人的4007幅人脸，每个人含有1～22幅具有不同表情的人脸。本文采用40个人的240幅人脸进行实验，选取每个人的一张中性人脸共 40幅人脸作为库集，其余作为测试集，即All vs. Neutral实验，其中测试集包含带有微笑、大笑、皱眉、鼓腮、吃惊等表情的非中性人脸，如图5所示。

图5 不同表情人脸

4.1 识别实验

本文在 FRGC v2.0数据库上进行了一系列的实验来进行验证。首先需分别进行分层弹性匹配和点距对应匹配实验。

提取人脸曲面上的 36条径向曲线并进行重采样，在FRGC v2.0数据库上进行分层弹性匹配识别实验；然后，对重采样后的曲线进行有用点提取，进行点距对应匹配识别实验。两种实验的累积匹配特性(cumulative match characteristic,CMC)曲线如图6所示。

由图 6可知，分层匹配单独用于识别时Rank-1识别率为 91.5%，点距对应匹配时的Rank-1识别率为76.5%。分层弹性匹配时包含曲线局部和整体的特征，但由于仅采用了曲线采样点的二维坐标信息，舍弃了一维坐标信息，因而识别率不是很高。点距对应匹配仅采用了曲线采样点相对鼻尖点的空间距离，因而识别率较低，但很好地保留了点的空间三维信息，弥补了分层弹性匹配的不足。为了保证更高的识别率，本文在分层弹性匹配中融合点距对应匹配，识别结果如图6最高曲线所示。

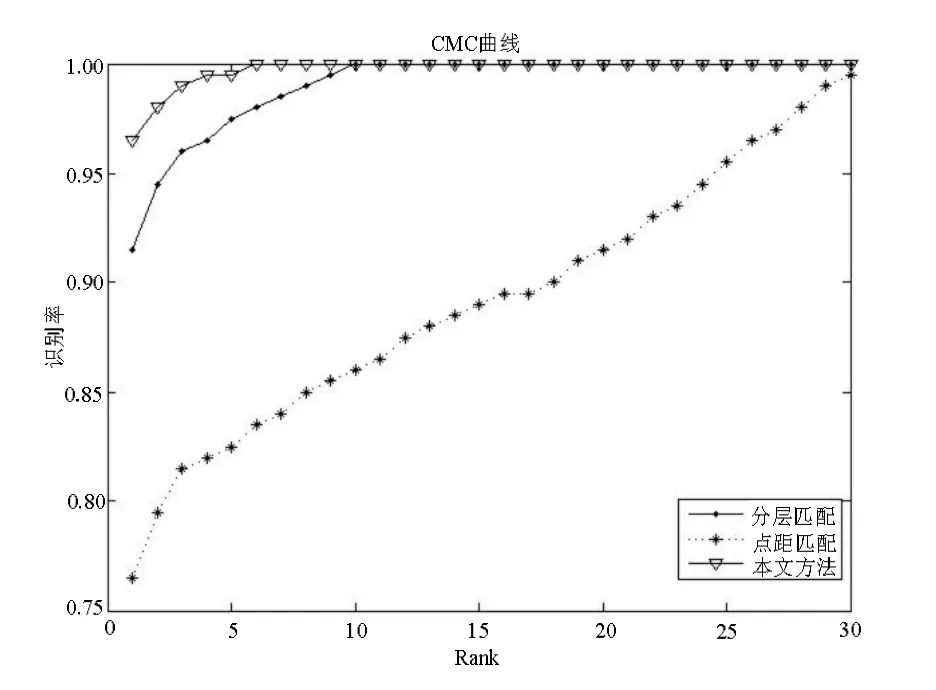
图6 CMC曲线

4.2 表情鲁棒性实验

我们分别做了两种实验来验证本文方法对表情的鲁棒性，首先验证对不同曲线分配权重的有效性实验，本文选取所有选定的库集和测试集人脸进行识别实验，实验结果如图7(a)所示，分配权重后点距匹配、分层匹配和整体匹配识别率分别上升了8%、4%和2.5%，说明对不同曲线分配不同的权重能有效地提高人脸识别率。

将测试集中的人脸分为122幅有表情人脸和78幅无表情人脸分别与库集进行识别实验，识别结果如图7(b)所示，在无表情的情况下，点距匹配、分层匹配和整体匹配识别率分别为79.48%、96.15%和 98.72%，而在有表情的情况下，识别率分别为64.75%、86.89%和93.44%，从结果可知采用本文方法进行整体匹配时识别率仅下降5.28%，远小于其他两种方法，说明本文方法对表情变化具有较好的鲁棒性。

为了进一步证明本文方法对表情变化的鲁棒性，与FRGC数据库提供的基准算法ICP进行比较。在无表情和有表情的情况下，ICP算法的识别率分别为83.33%和71.31%，识别率下降了12.02%，本文只下降了5.28%，可以看出本文方法比ICP算法具有更好地识别率并且对表情变化具有较好的鲁棒性。

以上3种实验证明本文方法通过对不同曲线分配不同的权重和分层匹配算法包含点距信息的方法，有效地减少了表情变化的影响，说明本文方法对表情的变化具有较好的鲁棒性。

图7 表情鲁棒性实验

4.3 实验结果分析

表1中列举了一些在FRGC数据库上进行实验的相关三维人脸识别方法。Berretti等[10]根据曲面点到鼻尖的测地距离将人脸划分为若干个等测地区域，然后根据对应等测地区域上的点之间的位置关系来识别人脸，该方法由于考虑了人脸区域的所有点因而识别率很难提高，同时测地距离计算时间较大，影响人脸识别效率。Mian等[19]首先使用一种三维局部特征和二维局部特征尺度不变变换特征（scale invariant feature transform，SIFT）的联合描述符组成拒绝分类器，排除库集中的大部分人脸，然后选取三维人脸的额头和鼻子区域与剩下的库集人脸进行 ICP匹配，整个算法较为复杂，且最后用到ICP算法，时间效率较低。Faltemie等[20]提出的识别算法具有较好的识别性能，但识别时间非常长。

表1 算法结果比较

与其他识别方法相比，本文方法提取能够表征人脸曲面的径向曲线集，曲线的分层弹性匹配算法很好地利用了曲线的整体和局部几何信息克服了人脸的形变影响，同时融合了曲线上点到鼻尖点的距离信息，因而具有较高的识别率。

4.4 时间代价分析

在机器配置为 Core(TM) i3-2100 CPU 3.10 GHz，4.0 GB内存上使用C++编程。分层弹性匹配算法采用了递归思想，使用动态规划编程实现。经过中点的搜索范围缩小改进之后，每条线的匹配时间复杂度为 O (n m3)。

一幅人脸的识别过程包括预处理，曲线提取和识别等过程，其中预处理部分由于原始的人脸模型包含耳朵、头发和肩膀等冗余区域数据量很大，因而预处理时间较长为2.6 s。曲线的提取占据很少部分时间，说明本文使用的径向曲线提取简单、快速和有效。表2列举了部分三维人脸识别算法完成一幅测试人脸与 FRGC v2.0数据库上总共466幅库集人脸一次识别所用的时间。

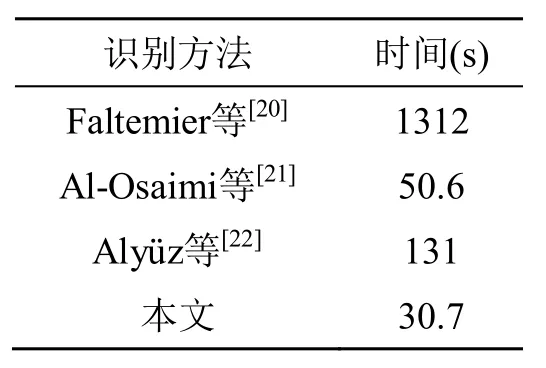
表2 时间代价分析

Faltemie等[20]提出的识别算法具有较好的识别性能，但识别时间非常长，Al-Osaimi[21]， Alyüz等[22]提出的算法识别性能已有很大提升。从表2中可以看出本文识别算法相比其他算法识别耗时较小，在库集人脸为466幅时，总耗时为30.7 s，在可接受范围之内。

5 总结与展望

本文提出了一种基于曲线分层弹性匹配的三维人脸识别方法，该方法首先提取能够表征人脸曲面的径向曲线集，然后对径向曲线进行重采样和有用点提取，对重采样后的曲线进行分层弹性匹配，同时结合曲线上的有用点到鼻尖点的距离信息进行人脸识别，实验结果证明了本文方法的有效性。本文方法有如下特点：

（1）曲线分层弹性匹配算法很好地利用了曲线的整体和局部几何信息，对形变图形的匹配具有很好的效果；本文方法对曲线的平移、旋转和尺度变化具有不变性，很好地克服了人脸的曲面形变；对分层匹配算法的中间点搜索进行优化，大大减少了曲线匹配的时间代价。

（2）对每条径向曲线根据其受表情影响的严重程度给予不同的权重，对处在额头等刚性区域的曲线给予较大权重，对处在嘴巴区域的曲线给予较低权重，这样就能够有效克服表情变化带来的影响。

（3）通过建立曲线采样点之间的对应关系，对径向曲线进行有用点的提取，有效地减少了数据丢失和头发遮挡等因素对人脸识别效果的影响。

本文算法实现简单，效果较好，下一步主要将其运用到实际的人脸识别系统中，针对具体的应用环境进行相应的改进。

[1] Blanz V,Vetter T. Face recognition based on fitting a 3D morphable model [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(9): 1063-1074.

[2] Besl P J,McKay H D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2): 239-256.

[3] Pan Gang,Wu Zhaohui,Pan Yunhe. Automatic 3D face verification from range data [C]//International Conference on Acoustics,Speech and Signal Processing (ICASSP),2003: 193-196.

[4] Givens G,Beveridge J R,Draper B A,Bolme D. A statistical assessment of subject factors in the PCA recognition of human faces [C]//Proceedings of the 2003 Conference on Computer Vision and Pattern Recognition Workshop,2003: 96-103.

[5] Horn B K. Extended Gaussian image [J]. Proceedings of the IEEE,1984,72(12): 1671-1686.

[6] 徐 俊,达飞鹏. 一种基于局部描述符的三维人脸识别方法[J]. 模式识别与人工智能,2012,25(1):45-53.

[7] Beumier C,Acheroy M. Automatic 3d face authentication [J]. Image and Vision Computing,2000,18(4): 315-321.

[8] Samir C,Srivastava A,Daoudi M. Three-dimensional face recognition using shapes of facial curves [J].IEEE Transactions on Pattern Analysis and Machine Intelligence 2006,28(11): 1858-1863.

[9] Samir C,Srivastava A,Daoudi M,Klassen E. An intrinsic framework for analysis of facial surfaces [J].International journal of Computer Vision,2008,82(1):80-95.

[10] Berretti S,Del Bimbo D,Pala P. 3D Face Recognition using iso-Geodesic Stripes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(12): 2162-2177.

[11] Gokberk B,Irfanoglu M O,Akarun L. 3D shapebased face representation and feature extraction for face recognition [J]. Image and Vision Computing,2006,24(8): 857-869.

[12] Li Chao,Barreto A,Zhai Jing,Chin C. Exploring face recognition by combining 3D profiles and contours [C]//Proceedings of the IEEE Conference on Southeast Con,2005: 576-579.

[13] Felzenszwalb P F,Schwartz J D. Hierarchical Matching of Deformable Shapes [C]//IEEE Conference on Computer Vision and Pattern Recognition,2007: 1-8.

[14] 李晓莉. 表情变化条件下的三维人脸识别研究[D].南京: 东南大学自动化学院,2010.

[15] Dorai C,Jain A K. A representation scheme for 3D free-form objects [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(10):1115-1130.

[16] Krepela M,Zahradnik D,Sequens J. Possible methods of Norway spruce (Picea abies [L.] Karst.)stem shape description [J]. Journal of Forest Science,2005,51(6): 244-255.

[17] Dryden I L,Mardia K V. Statistical shape analysis [M].John Wiley and Sons,1998.

[18] Bronstein A M,Bronstein M M,Kimmel R.Expression-invariant representation of faces [J].IEEE Transactions on Image Processing,2007,16(1):188-197.

[19] Mian A,Bennamoun M,Owens R. Face recognition using 2D and 3D multimodal local features [C]//International symposium on visual computing,2006:860-870.

[20] FaltemierT C,Bowyer K W,Flynn P J. A region ensemble for 3-d face recognition [J]. IEEE Transactions on Information Forensics and Security,2008,3(1): 62-73.

[21] Al-Osaimi F,Bennamoun M,Mian A. An expression deformation approach to non-rigid 3D face recognition [J]. International Journal of Computer Vision,2009,81(3): 302-316.

[22] Alyüz N,Gökberk B,Akarun L. Regional registration and curvature descriptors for expression resistant 3D face recognition [C]//Proceedings of the IEEE 17th signal processing and communications applications conference,2009: 544-547.