求解机组组合问题的改进型人工鱼群算法研究
2014-07-08翟军臣杜廷松李德宜李文武
翟军臣,杜廷松,,李德宜,李文武
1.三峡大学非线性与复杂系统研究所,湖北宜昌 443002
2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,武汉 430081
3.三峡大学电气与新能源学院,湖北宜昌 443002
◎工程与应用◎
求解机组组合问题的改进型人工鱼群算法研究
翟军臣1,杜廷松1,2,李德宜2,李文武3
1.三峡大学非线性与复杂系统研究所,湖北宜昌 443002
2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,武汉 430081
3.三峡大学电气与新能源学院,湖北宜昌 443002
提出了改进型人工鱼群算法。采用线性递减的函数取代标准人工鱼群算法(BAFSA)中的固定视野;在觅食行为中,利用粒子群算法(PSO)中的惯性权重线性递减的视野来加速算法的收敛速度;同时用混沌现象代替BAFSA中的随机现象。给出了算法的全局收敛性证明,并将算法应用于求解电力系统机组组合问题,分别对基准测试函数、三机组和十机组系统进行仿真计算,结果均表明新算法能有效跳出局部极值,收敛速度快且具有更高的精度。因此,改进型算法可以作为求解机组组合问题的有效算法。
机组组合;人工鱼群;线性递减;混沌搜索
1 引言
电力系统的中大规模机组组合(UC)问题是一个高维、离散、非线性的工程优化问题[1]。其机组调度的目的是在一个周期内满足各种约束的条件下动态地决策机组的启停和安排机组出力,使得机组总耗量最小。当系统的规模较大时,要从理论上求得精确的最优解已相当困难。由于传统的优化算法在求解UC问题过程中都或多或少地存在一些缺陷,往往得不到较理想的全局最优解;而现代智能优化算法因处理约束方便、全局搜索能力强而倍受众多学者关注。这些现代智能优化算法如PSO、遗传算法[2](GA)、人工神经网络[3](NN)、禁忌搜索(TS)、模拟退火[4](SA)、模糊优化等方法已成功应用于这类问题的求解。
BAFSA是一类基于动物行为的群体智能优化算法[5]。该算法具有简单易实现、收敛速度快、计算效率较高等优点,其对初值与参数选择不敏感,具有较强的鲁棒性和较好的收敛性能,但是寻优结果精度低且易陷入局部最优,出现早熟现象。因此,学者们从不同的方面对人工鱼群算法进行了改进。文献[6]引入生存机制和竞争机制对算法进行改进,所给算法的收敛速度和搜索效率得到一定程度的提高;文献[7]引入鱼的吞食行为,以减少算法的运算量,提高运算速度,并提高算法跳出局部极值的能力;文献[8]采用最优个体保留策略对鱼群算法的觅食行为进行改进,给出加速个体局部搜索方法。这些改进算法在一定程度上改善了BAFSA的优化性能,但算法运行后期搜索的盲目性较大、易陷入局部最优和寻优结果精度低等问题没有得到很好地解决。
本文提出了一种改进的人工鱼群算法(IAFSA),采用线性递减的函数来代替不变的视野值;在觅食行为中引入惯性权重线性递减的视野;同时引入混沌行为代替随机行为。新算法可保证快速地收敛到最优解,并且避免陷入局部极值而出现早熟现象。
2 BAFSA基本框架
在一片水域中,鱼往往能自行或尾随其他鱼找到营养物质多的地方,因而鱼生存数目最多的地方一般就是本水域中营养物质最多的地方。BAFSA就是根据这一特点,通过构造人工鱼来模拟鱼群的觅食、聚群、追尾及随机行为,从而实现寻优[9-10]。
2.1 相关定义
人工鱼个体的状态可以表示为向量X=(x1,x2,…,xn),xi(i=1,2,…,n)为欲寻优的变量;人工鱼当前所在位置的食物浓度可以表示为Y=F(X),其中Y为目标函数值;人工鱼个体i,j之间的距离为dij=‖Xi-Xj‖;step表示人工鱼移动的最大步长;Visual表示人工鱼视野;try_number表示尝试次数;δ表示拥挤度因子;N表示人工鱼总数。
2.2 行为描述
(1)觅食行为
这是人工鱼的一种基本行为,也就是趋向食物的一种活动。设人工鱼i当前状态为Xi,在其感知范围内随机选择一个状态Xk:

式中,Rand()是一个介于0和1之间的随机数,如果在求极大值问题中,Yi<Yj,则向该方向前进一步:
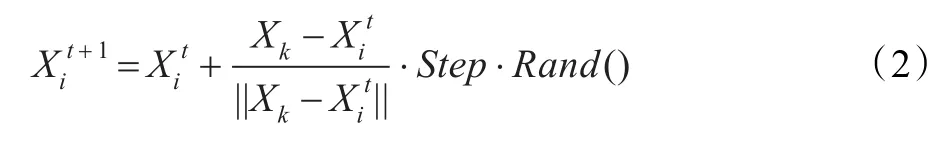
否则,再重新随机选择状态Xk,判断是否满足前进条件。这样反复尝试try_number次后,如果仍不满足前进条件,则执行随机行为。
(2)聚群行为

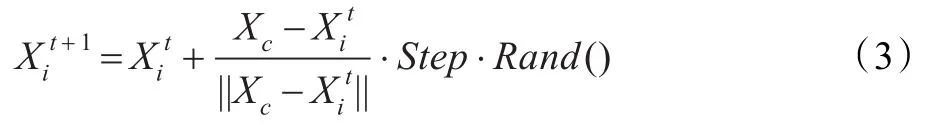
否则,执行觅食行为。
(3)追尾行为


否则,执行觅食行为。
(4)随机行为
随机行为的实现较简单,就是在视野中选择一个状态,然后向该方向移动,其实,它是觅食行为的一个缺省行为,即Xi的下一个位置为:
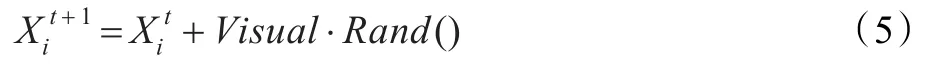
3 改进型人工鱼群算法
3.1 改进措施
(1)一般来讲,当视野范围较小时,人工鱼群的觅食行为和随机游动比较突出,可能导致算法陷入局部最优解;视野范围较大时,人工鱼的追尾行为和聚群行为将变得较突出,较容易发现全局极值并收敛,而人工鱼在比较大的区域内执行觅食行为和随机行为,不利于全局极值附近的人工鱼发现邻近范围内的全局极值点。故对人工鱼的视野进行适当的改变:在算法的初始阶段,每条人工鱼以一个大的视野寻找解,这样能扩大寻优的范围。随着算法进化代数的增加,鱼群的视野将适当地减小以加快收敛速度,提高算法的优化性能。因此,采用线性递减的视野,定义视野的变化函数为:
其中,gen为当前进化代数,V(gen)为gen代人工鱼视野值,Vmax,Vmin分别是视野的上下限,MAXGEN为最大进化代数。算法初期人工鱼的视野越大,就越容易发现全局最优值并收敛,随着进化程度的不断加深,视野不断地减小,算法越有利于局部搜索。
(2)对觅食行为中人工鱼的视野作进一步改进,当人工鱼在其感知范围内随机选择下一个状态时,利用PSO中惯性权重线性递减的视野代替原来的视野[11],加速算法的收敛速度。具体如下:
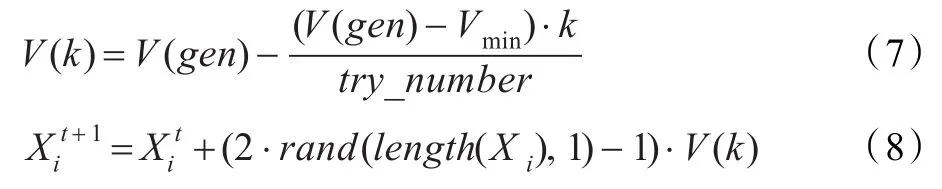
其中,V(k)为一次迭代中觅食行为第k次尝试的视野;k和try_number分别表示当前尝试次数和最大尝试次数;是当前状态,X为下一个状态。随着尝试次数的增加,惯性权重不断减小,感知范围的半径也随着不断的减小,保证了算法能够快速地收敛到最优解。
(3)混沌运动具有遍历性随机性等特性,能够在一定的范围内按其自身规律不重复遍历所有状态[12]。因此,在BAFSA中的随机行为将混沌搜索引入其中,即用混沌现象代替随机现象。
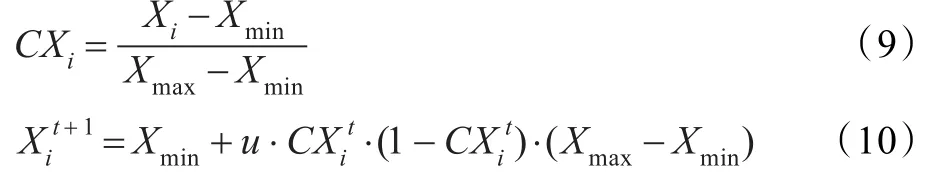
其中,CXi为混沌变量,u为控制参数,Xmax、Xmin分别为Xi的最大值和最小值,是当前状态,X为下一个状态。混沌现象执行简单并且能够避免陷入局部极值。
混沌映射式(10)为Logistic映射,取控制参数u=4时,式(10)处于混沌状态,也就是说除(0,0.25,0.5,0.75,1)这几个点外,其他点都是通过迭代公式产生的,它们都处于0和1之间。因为混沌现象的轨迹对初始值非常敏感,如果n个决策变量的初始值不同,就可以得到n个不同的混沌轨迹。
IAFSA步骤如下:
步骤1初始化设置,包括人工鱼群的个数N、每条人工鱼的初始值位置、人工鱼移动的最大步长(Step)、人工鱼的初始视野(Visual),最大进化代数(MAXGEN)、重试次数(try_number)和拥挤度因子(δ)。
步骤2利用公式(6)计算人工鱼当前的视野值,计算每条人工鱼的适应度值,并记录全局最优的人工鱼的状态。
步骤3对每条人工鱼进行评价,对其要执行的行为进行选择,包括觅食行为、聚群行为、追尾行为和随机行为。
步骤4执行人工鱼选择的行为,四种行为分别对应于公式(8)、(3)、(4)、(10),根据对应公式计算每条人工鱼的适应度值,更新每条人工鱼的位置信息。
步骤5更新全局最优人工鱼的状态。
步骤6判断是否满足终止条件,若满足,则输出结果,否则,跳转到步骤2。
3.2 算法的应用
在实际情况中,汽轮机进气阀突然开启时会产生阀点效应,该效应对于最优分配的求解影响明显[13]。文中研究的是一个静态计及阀点效应的机组组合优化问题,模型中对负荷平衡、机组技术出力等实际情况进行约束,建立了追求发电成本最小的机组组合优化数学模型。
考虑阀点效应后的耗电特性为:

其中,Fi为第i台发电机的发电费用,Pi为第i台发电机的有功功率,ai、bi、ci为第i台发电机的运行特性参数,ei,fi为第i台发电机的阀点效应系数,Pimin为第i台发电机的最小出力。
综上所述,计及阀点效应的机组优化数学模型如下:

其中,F为总的发电费用,N为系统内发电机的总数,PL为系统负荷,PD为系统网损,Pimin,Pimax分别是机组出力的最小值和最大值。当电力系统网络覆盖密集时可以忽略网损,文中在计算时忽略了系统网损。
BAFSA是通过迭代搜寻最优解的,在每次迭代的过程中,人工鱼都通过觅食、聚群、追尾和随机等行为来更新自己。根据机组发电功率的最大值和最小值产生初始的人工鱼群:
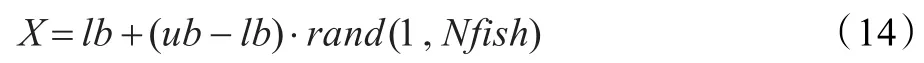
其中,ub和lb分别是机组发电功率的最大值和最小值;X为初始的人工鱼群状态。引进惩罚因子,将UC的目标函数转化为:

其中,λ为惩罚因子。设人工鱼当前状态为Xi,探索当前领域内(dij≤Visual)的伙伴数目nf及中心状态Xc。若Yc/nf≥δYi,人工鱼执行聚群、追尾等行为。否则,执行觅食行为(8):
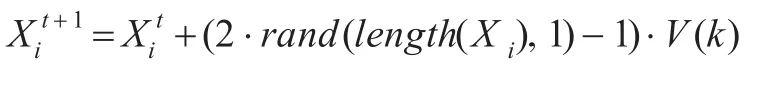
若Xj不在感知范围内,则执行改进后的随机行为式(10):

本次循环结束后,自动更新人工鱼的当前状态X和当前位置的食物浓度Y。当进化代数大于等于最大进化代数(gen≥MAXGEN)的时候,则停止运算并求出仿真计算中的全局近似最优解(机组总耗量最小)。
4 收敛性分析
4.1 概念及引理


其中,F(a)为目标函数;gi(a)为第i个约束条件;M为约束条件个数;a为n维未知变量;Z为搜索空间。当问题规模为n时,搜索空间Z为机组的组合变量空间,是一个离散的状态空间,状态数一共有|Z|=2n。令Y={F(a)|a∈Z},则有Y={F(a)|a∈Z},|Y|<|Z|。设|Y|=N,将Y具体化为:

定义人工鱼的食物浓度为:Energy(a)=F(a),a∈Z;令XZ为所有人工鱼集合,∀x∈XZ,有YN≤Energy(X)≤Y1,将集合XZ划分为非空子集:

令Xi,j(i=1,2,…,N,j=1,2,…,|表示中第j个人工鱼的位置状态。在人工鱼的行为过程中,从一个状态转移到另外的状态可表示为Xi,j→Xk,l,则从Xi,j到Xk,l的转移概率为pij,kl,从Xi,j到X中任一人工鱼位置状态的转移概率为pij,k,从X中任一人工鱼位置状态到中任一人工鱼位置状态的转移概率为pi,k,则有[14]:


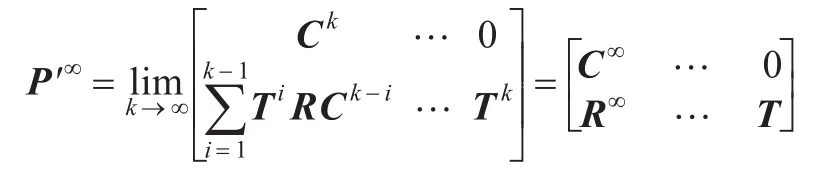
P′∞为一个稳定的随机矩阵,且P′∞=1′P′∞,P′∞= P′0P′∞唯一确定并且与初始分布无关,P′∞满足如下条件:

4.2 全局收敛性证明
定理1在改进型人工鱼群算法中,对于∀Xi,j⊂,i=1,2,…,N,j=1,2,…,|X|满足:

证明设Xi,j为第t次迭代后的人工鱼,记为Xt,设在Xt中能量最高的人工鱼为bestt=X*,其中,bestt为n维矢量,则有F(bestt)=Y1。在BAFSA中,每次迭代过程中对当前人工鱼最优状态的更新可知:
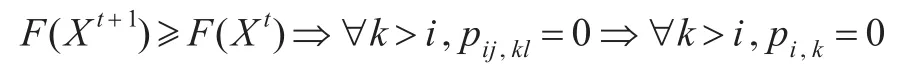
式(18)得证。
对于式(19),由BAFSA中对每个人工鱼探索其当前所处的环境状况,选择一种行为(觅食、聚群或者追尾),设bestt+1为Xt+1中最优人工鱼。采取线性递减的函数值代替固定的视野,只改变人工鱼选择行为的概率值,仅对收敛速度产生影响,而不影响算法的收敛性。以下分情况进行分析:
情况1如果人工鱼选择聚群行为或追尾行为,即选择聚群行为概率ps>0或选择追尾行为概率pf>0,则有F(bestt+1)>F(bestt),结论显然成立。
情况2如果当前人工鱼选择觅食行为,说明此时当前人工鱼在邻域内为最优,则此时人工鱼选择此种行为的概率pp=1-ps-pf,此时人工鱼探索感知范围随机选择状态,有两种情况:
(1)选择的状态位置食物浓度高于当前食物浓度,设此种情况的概率为ppy,命题得证。
(2)选择状态位置食物浓度低于当前人工鱼位置食物浓度,设此种情况的概率为ppn=1-ppy,此时重新选择,反复尝试try_number次,则其概率为(ppn)try_number;如果仍不满足,则随机移动,设随机移动的概率为prandom,注意到用混沌现象代替随机现象不会影响随机运动的概率。随机移动后状态位置浓度高于当前人工鱼位置食物浓度的概率为pbetter=(1/2)(1-(ppn)try_number× prandom)≥0;如果pbetter>0,命题得证;如果pbetter=0,说明此时人工鱼已经到达局部极值。此时通过设置较小的try_number可以使其随机移动,跳出局部极值。

表1 10维函数BAFSA、GAFSA和IAFSA算法结果比较
由基本人工鱼群算法可知,人工鱼选择一种行为的总概率为1,即ps+pf+pp=1,综合上述两种情况可得,∃k<i,pik>0,证毕。
定理2改进型人工鱼群算法具有全局收敛性。

根据定理1中式(19)结论得:

由以上可知,转移矩阵P′是n阶可归约随机矩阵,满足上述引理1中条件,所以,下式成立:
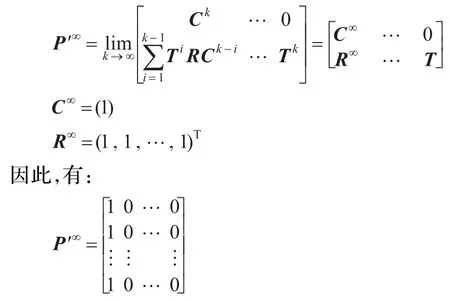
该矩阵是稳定的随机矩阵,故可得:

其中,Fbest为最优目标函数值,即Fbest=f(Xt)。因此,改进型人工鱼群算法具有全局收敛性,证毕。
5 仿真实验
5.1 典型函数仿真实验
为验证IAFSA的有效性,采用如下三个基准测试函数进行仿真计算,并与BAFSA和文献[16]提出的全局版人工鱼群算法(GAFSA)进行比较。

上述三个多维函数,理论最小值均为0。
设定参数如下:人工鱼数目N=40,最多尝试次数try_number=9,视野半径visual=1,拥挤度因子δ= 0.618,步长step=0.5,上述三个函数变量取10维,用BAFSA、GAFSA和IAFSA分别对三个典型函数求m in,最大进化代数设置为1 500次,连续运行50次,将所得的函数全局平均最小值(Amin)、函数全局最小值(Gmin)和标准差(σ)作为算法性能的衡量指标,所得结果如表1。
图1~3是10维函数f1,f2,f3采用BAFSA、GAFSA和IAFSA运行50次后得到的平均最小值进化曲线,图中纵坐标用函数最优平均值的自然对数表示。
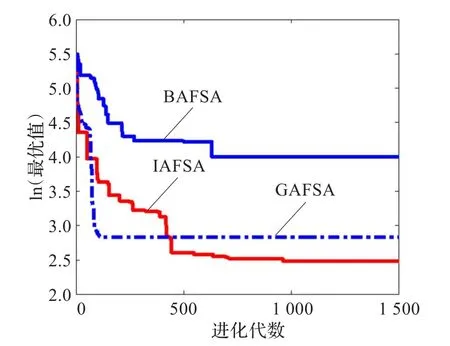
图1 函数f1平均最小值的进化曲线
从实验的结果可以看出,IAFSA的平均优化结果和最优结果明显好于GAFSA和BAFSA,并且优化结果的精度远大于GAFSA和BAFSA,同时通过标准差的对比可以看出,IAFSA的稳定性比GAFSA和BAFSA都要好一些。

图2 函数f2平均最小值的进化曲线
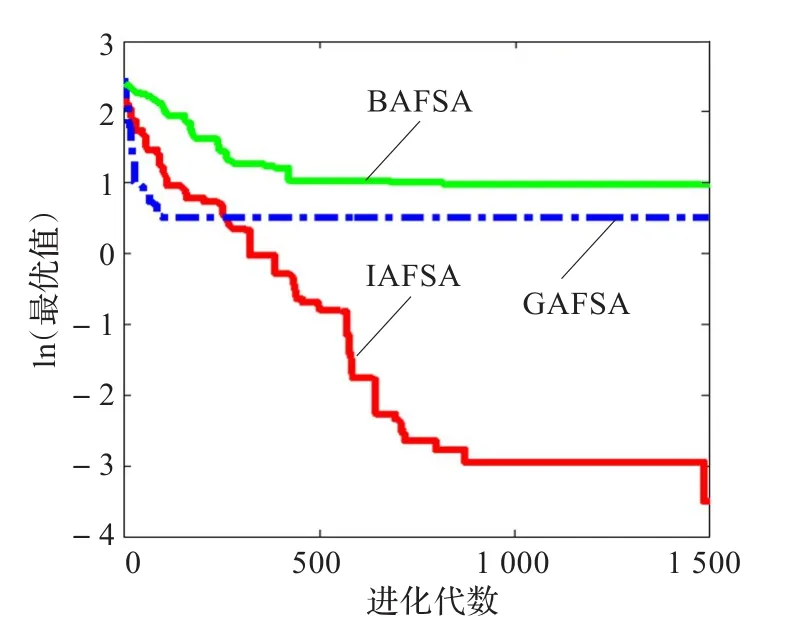
图3 函数f3平均最小值的进化曲线

表2 三机组系统BAFSA和IAFSA算法结果比较

表3 十机组系统BAFSA和IAFSA算法结果比较

图4 三机组系统BAFSA和IAFSA算法收敛曲线

图5 十机组系统BAFSA和IAFSA算法收敛曲线
5.2 机组组合系统仿真
为进一步验证文中提出的算法的有效性,分别对三机组和十机组系统进行仿真分析,机组参数、负荷需求等数据引用于文献[17-18]中。算法参数取:人工鱼数目N=200,最大进化代数MAXGEN=300,最多尝试次数try_number=100,视野半径visual=25,拥挤度因子δ=9,步长step=8。
5.2.1 三机组系统
对三机组系统用本文提出的IAFSA进行仿真计算,将得到的结果与BAFSA进行比较,对改进后的程序运行30次取平均值,结果见表2。
从表2可以看出,IAFSA与BAFSA相比,效果较好,新型算法在精度上有了较大的提高,并且收敛速度也更快。BAFSA计算得到的近似最优解为5 122.347$,平均耗时90.472 5 s;而IAFSA计算得到的近似最优解为5 095.705$,平均耗时15.922 6 s。IAFSA在精度方面提高了0.5%,平均耗时方面提高了82.4%。
5.2.2 十机组系统
用本文提出的IAFSA进行仿真计算,将得到的结果与BAFSA进行比较,对改进后的程序运行30次取平均值,结果见表3。
从表3可以看出,对于十机组系统IAFSA与BAFSA相比,效果较好,改进的算法在精度上有了很大的提高。
5.2.3 结果分析
为验证算法改进的作用,将三机组和十机组系统BAFSA和IAFSA算法收敛过程的收敛特性作对比,收敛曲线如图4和图5所示。
从图4和图5可以看出,BAFSA容易陷入局部最优解,出现早熟的现象。IAFSA能够有效地跳出局部极值,经过不断迭代寻优,最终趋于稳定。
6 结束语
本文评述了BAFSA的规则和特点,提出了改进型人工鱼群算法,并将其用于求基准测试函数的最小值和求解电力系统机组组合问题。采用线性递减的视野函数,保证算法快速跳出局部极值区域,加快了该算法的收敛速度;当人工鱼在其感知范围内随机选择下一个状态时,利用PSO中的惯性权重线性递减来加速算法的收敛速度;用混沌现象代替BAFSA中的随机现象,避免了算法丢失最优解而陷入搜索停滞即出现早熟的现象。基准测试函数、三机组和十机组系统的仿真计算结果均表明改进型算法是求解机组组合问题的有效算法。
[1]陈皓勇,王锡凡.机组组合问题的优化方法综述[J].电力系统自动化,1999,23(4):51-56.
[2]朱宗斌,杜中军.基于改进GA的云计算任务调度算法[J].计算机工程与应用,2013,49(5):77-80.
[3]杨静俐,杜廷松.求解线性约束的二次规划神经网络学习新算法[J].计算机工程与应用,2010,46(24):37-39.
[4]李梓,于海涛,贾美娟.基于改进模拟退火的优化k-means算法[J].计算机工程与应用,2012,48(24):77-80.
[5]Ma Jun.Research on the fish behavior simulation based on swarm intelligence[J].Procedia Engineering,2002,43:547-551.
[6]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.
[7]Cheng Y M,Jiang M Y,Yuan D F.Novel clustering algorithms based on improved artificial fish sw arm algorithm[C]//Proceedings of the 6th International Conference on Fuzzy Systems and Know ledge,2009:141-145.
[8]范玉军,王冬冬,孙明明.改进的人工鱼群算法[J].重庆师范大学学报:自然科学版,2007,24(3):23-26.
[9]Jiang Jingqing,Bo Yuling,Song Chuyi,et al.Hybrid algorithm based on particle sw arm optimization and artificial fish swarm algorithm[J].Lecture Notes in Computer Science,2012,7367:607-614.
[10]Tsai Hsing-Chih,Lin Yong-Huang.Modification of the fish swarm algorithm with particle swarm optimization formulation and communication behavior[J].Applied Soft Computing,2011,11(8):5367-5374.
[11]Simon S P,Padhy N P,Anand R S.An ant colony system approach for unit comm itment problem[J].Electrical Power and Energy Systems,2006,28:315-323.
[12]Yuan Xiaofang,Yang Yim in,Wang Hui.Improved parallel chaos optimization algorithm[J].Applied Mathematics and Computation,2012,219(8):3590-3599.
[13]蒋秀洁,龚学会,李沧.基于MATLAB的计及阀点效应的有功功率经济分配[J].电力学报,2008,23(6):467-469.
[14]黄光球,刘嘉飞,姚玉霞.人工鱼群算法的全局收敛性证明[J].计算机工程,2012,38(2):204-206.
[15]Iosifescu M.Finite Markov processes and their applications[M].New York:John W iley Sons,1980.
[16]王联国,洪毅,施秋红.全局版人工鱼群算法[J].系统仿真学报,2009,21(23):7483-7486.
[17]Liao Daqian,Du Tingsong.Improvement on particle swarm optimization method solving unit comm itment dispatch in the power system considering the valve-point effect[C]// Proceedings of 2012 the 3rd International Conference on Mechanic Automation and Control Engineering. USA:IEEE Press,2012:323-326.
[18]吴月萍,杜奕.改进的人工鱼群算法的参数分析[J].计算机工程与应用,2012,48(13):48-52.
ZHAI Junchen1,DU Tingsong1,2,LI Deyi2,LI Wenwu3
1.Institute of Nonlinear and Complex Systems, China Three Gorges University, Yichang, Hubei 443002, China
2.Hubei Province Key Laboratory of System Science in Metallurgical Process, Wuhan University of Science and Technology,Wuhan 430081, China
3.College of Electrical Engineering and Reusable Energy, China Three Gorges University, Yichang, Hubei 443002, China
An improved artificial fish swarm algorithm is proposed. The new algorithm uses the linear decreasing function instead of a fixed visual, uses linear decreasing inertia weight as the Particle Swarm Optimization(PSO)to accelerate the convergence speed of the algorithm, and uses chaos phenomenon instead of random phenomena of BAFSA. It presents the global convergence proof and carries on the simulation experiment with the test function and the systems of three units and ten units. The results show that the improved algorithm can escape from the local extremum effectively, and has higher convergence speed and precision. So it can be used as an effective algorithm for combined allocation problem.
unit commitment; Artificial Fish Swarm Algorithm(AFSA); linear decreasing; chaos search
ZHAI Junchen, DU Tingsong, LI Deyi, et al. Improved artificial fish swarm algorithm for combined allocation problem. Computer Engineering and Applications, 2014, 50(17):223-229.
A
TP301
10.3778/j.issn.1002-8331.1310-0198
国家自然科学基金(No.61174216,No.61374028);湖北省自然科学基金(No.2013CFA 131);冶金工业过程系统科学湖北省重点实验室(武汉科技大学)开放基金(No.z201402)。
翟军臣(1988—),男,硕士研究生,主要研究领域为人工智能在电力系统中的应用、数值计算;杜廷松(1969—),男,通讯作者,教授,主要研究领域为最优化理论与算法、智能计算;李德宜(1962—),男,教授,主要研究领域为凸体理论与控制理论;李文武(1975—),男,副教授,主要研究领域为电力系统信息安全、水电站仿真与控制及配电网分析。E-mail:tingsongdu@ctgu.edu.cn
2013-10-17
2013-11-25
1002-8331(2014)17-0223-07
CNKI网络优先出版:2014-03-12,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0198.htm l
