一种基于三元联系数的语言区间信息集结方法

王万军

兰州文理学院信息工程学院，兰州 730000

一种基于三元联系数的语言区间信息集结方法

王万军

兰州文理学院信息工程学院，兰州 730000

给出利用属性权重与信息决策解决语言区间信息集结的三元联系数问题的新方法。其主要思路是将语言区间变量转化为对应三元联系数矩阵，并通过对该矩阵最优集结，建立三元联系数多属性优化函数及语言区间属性权重区间数。然后进行集对势分析，计算势关联度大小并择优排序。通过实例说明该算法的处理过程及有效性。

三元联系数；语言区间；信息集结方法

1 引言

语言区间信息集结是决策科学中一个非常重要的研究方向和热点，在属性值或实数值语言信息决策中有相对完善的理论和方法[1-4]。但在实际生活中，由于决策信息的复杂性、不确定性及人类认知问题模糊性等原因，使信息决策变得抽象化和复杂化。虽然，相关学者在该领域取得较为丰富的研究成果[5-13]，但仍存在不足和缺陷。例如，文献[5-6]研究了不同类型语言算子及其不确定语言信息集结问题，但不足之处是没有考虑决策中立情况；文献[7]给出了属性权重与属性值均为区间的多属性信息集结，该方法不足之处是没有有效处理不确定信息偏向趋势；文献[8-9]给出了不同偏好、具有依赖型的多属性信息集结，但该方法计算相对复杂，实际应用相对困难，过于理论化；文献[10-13]较为系统地给出了集对分析SPA（Sets Pair Analysis）[14]中联系数理论语言决策方法，但主要研究单值或单目标语言信息问题，没有涉及多值或不确定区间语言问题，从而不够全面。

本文在上述基础上，结合集对分析中三元联系数理论，初步研究了语言区间联系数信息集结问题。建立语言区间多属性优化目标函数，依据集对势关联度大小对信息进行择优决策。最后，通过实例说明该算法的具体计算过程。

2 语言区间与三元联系数

2.1 语言变量与语言区间

对语言区间进行信息集结时，通常采用9标度法，即：极差、很差、差、较差、一般、较好、好、很好、极好。将其建立在[0，1]上的一个论域集S来表示。即

定义1设语言标度S={si|i=-4，-3，-2，-1,0,1，2，3，4}，且满足如下条件：

（1）若i≥j，则si≥sj，若i≤j则si≤sj；

（2）若si≥sj，则si=max(si,sj)，若si≤sj，则si=m in(si,sj)。

此时称si为语言变量。

定义2对语言变量sL，sR，且sL≤sR，则称[sL，sR]为语言区间。

2.2 三元联系数

定义3[14]在集对分析中称μ=a+bi+cj，其中a，b，c∈[0，1]，a+b+c=1，j=-1，i∈[-1，1]为三元联系数。

定义4[15]对三元联系数μ=a+bi+cj（其中c≠0），称同一度a与对立度c的比值a/c为联系势或集对势，用Shi(H)=a/c表示。

当a/c=1，即a=c时，称为均势；当a/c＞1，即a＞c时，称为同势；当a/c＜1，即a＜c时，称为反势。

定义5[16]对联系数μ=a+bi+cj，当c=0时，称同一度a与差异度（不确定度）b的比值a/b为不确定联系势或不确定集对势，用Ushi(H)=a/b表示。

当a/b=1，即a=b时，称为不确定均势；当a/b＞1，即a＞b时，称为不确定同势；当a/b＜1，即a＜b时，称为不确定反势。

定义6对联系数μ=a+bi+cj，按a/c值排列的次序称为集对势序。

集对势序的关系为：同势优先于均势；均势优先于反势；势等级越小的优先于势等级越大的。

定义7集对大势是对同势、均势、反势、无穷大势和不确定势的一个统称。

定义8集对小势是对同一个同异反强度级别势的统称。

2.3 三元联系数语言信息转化

定义9对语言区间s=[sL，sR]，称μ=a+bi+cj= L+(R-L)i+(1-R)j为语言区间转化为三元联系数公式。其中称L为语言区间的确定性测度；R-L为语言区间的不确定测度；1-R为语言区间的对立测度。

3 三元联系数语言区间信息集结方法

设A={A1，A2，…，An}为方案集，G={G1，G2，…，Gm}为属性集，对于一个语言区间多属性信息集结问题，首先将方案集中语言区间的术语表示转化为对应九标度语言区间，方案Ai在属性Gj下的语言区间为[sL，sR]，由此构成语言区间信息矩阵。即

如果信息集结对方案Ai有主观偏好，主观偏好是以语言区间变量形式给出，即θi=[θLi，θRi]，i=1，2，…，m。则对偏好语言变量进行三元联系数转化。其转化采用[16-20]进行处理。即μθi=θLi+(θRi-θLi)i+(1-θRi)j。

定义10对三元联系数矩阵R˜与主观偏好三元联系数μθi，则称：

为偏差偏好联系数。

定义11对偏差偏好联系数μ∆ij，则称：

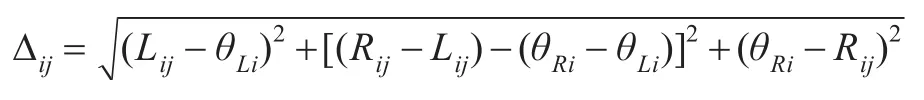
为偏差偏好联系数间距。

定义12对偏差偏好联系数μ∆ij，则称：

为偏差偏好联系数集对势。

在清楚上述的定义后，下面计算三元联系数语言信息集结总势关联系数δ∆ij。

定义13对偏差偏好联系数μ∆ij，则称：

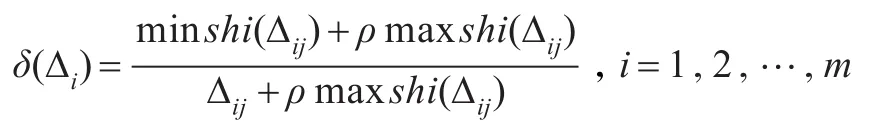
为三元联系数语言信息集结总势关联系数（度）。其中ρ为区分系数，ρ∈[0，1]，一般情况下ρ取值0.5。

这里δ(∆i)反映了方案Ai对所有主观偏好与客观偏好之间信息集结总势的关联情况，如果总势关联越大，则说明信息集结越优；否则，信息集结越劣。

为使信息集结结果具有合理性与有效性，属性权重ωj取值应使得信息集结的总势关联达到相似度最大。为此，建立确定权重ωj的多目标优化函数。

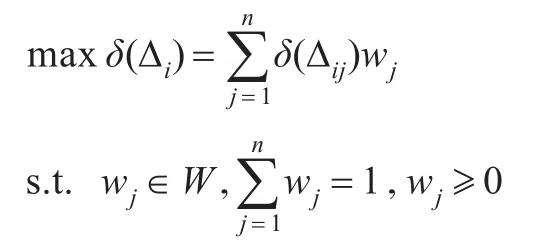
其中i=1，2，…，m;j=1，2，…，n。

同时，考虑信息集结的公平与合理，可以将确定权重ωj的多目标优化函数转化为单目标优化函数。

其中i=1，2，…，m;j=1，2，…，n。

求解该模型，得到权重向量ω，从而计算出总势关联度δ(∆i)大小。根据总势关联度大小进行信息集结。

基于上述分析，下面给出三元联系数语言区间信息集结算法的具体过程与步骤。

步骤1将方案集中语言区间术语表示转化为对应9标度语言区间信息矩阵。

步骤3将三元联系数矩阵R˜进行信息集结，利用定义10～12计算偏差偏好联系数势值shi(∆ij)。

步骤4利用定义13计算三元联系数语言信息集结总势关联度δ(∆ij)。

步骤5利用公式（1）计算权重向量。

步骤6计算带权重关联度δ(∆i)的大小并进行信息优劣判断。

4 算例分析

考虑一个大学的学院评估问题。某大学将采用对教学G1、科研G2和服务G3三个属性作为评估对象，对其下属的5个子学院Ai(i=1，2，3，4，5)进行评估。现得到评估矩阵如表1所示。而且对每个评估的属性权重W是以语言区间的形式给出。W为语言区间：ω1= [一般，好]，ω2=[一般，较好]，ω3=[较好，很好]。同时评估专家对各子学院的主观偏好为：

是根据上述信息评估最佳的学院。

表1 决策评估语言区间矩阵

下面利用本文方法进行信息集结评估。

步骤1把表1决策评估语言区间矩阵利用定义1转化为9标度语言区间信息矩阵。

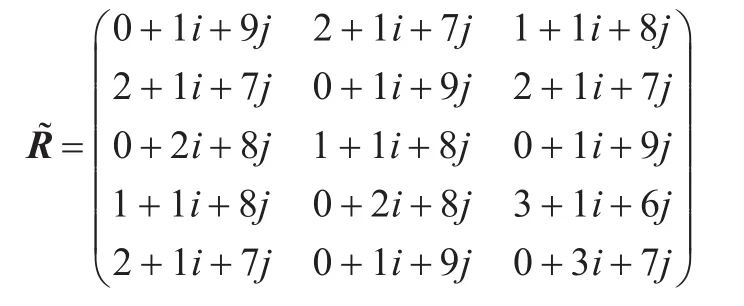
步骤3利用定义10～12计算偏差集对势值shi(∆ij)。

步骤4利用定义13计算总势关联度δ(∆ji)。

步骤5利用公式（1）计算权重向量，建立单目标最优化函数。

由于W为语言区间，且ω1=[一般,好]，ω2=[一般,较好]，ω3=[较好，很好]，利用定义9将其转化为三元联系数权重，并进行归一化处理。即得：

利用文献[21]将式（2）进行区间化处理，得到权重区间数为：

求解该优化函数模型，得权重向量：w=(0.4，0.2，0.4)。

步骤6计算带权重信息关联度δ，并进行优劣判断。

从而可知：5个子学院信息集结的结果为：A4≻A5≻A1≻A2≻A3。故A4评估结果最优。

这里需补充一点，对区分系数ρ取不同分辨系数，比如随机取ρ=0.01，0.5，0，8，经计算发现各信息集结果是一致的，这进一步说明该算法是有效的。

5 结论

本文给出了属性权重与信息决策均为语言区间多属性信息集结方法，该方法通过集对分析（SPA）中三元联系数思路解决了信息偏好为语言区间多属性信息集结问题，具有一定的实用性。该算法计算简单，行之有效。最后通过实例说明该方法的计算过程，并简要地分析其有效性。

[1]徐泽水.基于语言信息的决策理论与方法[M].北京：科学出版社，2008：8-53.

[2]徐泽水.直觉模糊信息集成理论与应用[M].北京：科学出版社，2008：45-61.

[3]徐泽水.不确定多属性决策方法及应用[M].北京：清华大学出版社，2006：161-178.

[4]卫贵武.基于模糊信息的多属性决策理论与方法[M].北京：中国经济出版社，2010：59-82.

[5]Wei Guiwu.Uncertain linguistic hybrid geometric mean operator and its application to group decision making under uncertain linguistic environment[J].International Journal of Uncertainty，Fuzziness and Know ledge-Based Systems，2009，17（2）：251-267.

[6]Xu Zeshui.On generalized induced linguistic aggregation operators[J].International Journal of General Systems，2006，35（1）：17-18.

[7]刘秀梅，赵克勤.基于二次联系数的区间数多属性决策方法及应用[J].模糊系统与数学，2011，25（5）：115-121.

[8]卫贵武.基于依赖型算子的不确定语言多属性群决策方法[J].系统工程与电子技术，2010，32（4）：764-769.

[9]卫贵武，黄登仕，魏宇.对方案有偏好的不确定语言多属性决策方法[J].管理学报，2007，4（5）：575-579.

[10]汪新凡，杨小娟.基于联系数贴近度的区间数多属性决策方法[J].数学的实践与认识，2008，38（3）：18-24.

[11]刘秀梅，赵克勤.基于联系数复运算的区间数多属性决策方法及应用[J].数学的实践与认识，2008，38（23）：57-64.

[12]刘秀梅，赵克勤.基于区间数确定性与不确定性相互作用点的多属性决策[J].数学的实践与认识，2009，39（8）：68-75.

[13]刘秀梅，赵克勤.基于SPA的D-U空间的区间数多属性决策模型及应用[J].模糊系统与数学，2009，23（2）：167-174.

[14]赵克勤.集对分析及其初步应用[M].杭州：浙江科学技术出版社，2000.

[15]王万军.基于联系数的不确定多属性决策方法[J].湛江师范学院学报，2008，29（4）：74-77.

[16]王万军.基于模糊决策的多属性联系数决策方法[J].数学的实践与认识，2008，38（21）：78-82.

[17]王万军.基于Vague集相似度量的一种联系数方法[J].计算机工程与应用，2012，48（1）：132-134.

[18]王万军，李恒杰.Vague值转化Fuzzy值的一种偏势方法[J].湖南师范大学学报：自然科学版，2012，35（4）：21-25.

[19]王万军，李恒杰，胡建军，等.一种Vague值转化Fuzzy值的偏联系数方法[J].计算机工程与应用，2013，49（1）：134-136.

[20]王万军，李恒杰，胡建军，等.一种SPA集转化Fuzzy集的新方法[J].计算机工程与应用，2013，49（3）：163-165.

[21]王万军.区间数排序的一种联系数方法[J].计算机工程与设计，2009，30（8）：2055-2057.

WANG Wanjun

College of Information Engineering, Lanzhou University of Arts and Science, Lanzhou 730000, China

This thesis proposes a new method to solve three element connection numbers of linguistic interval information aggregation by using the attribute weights and information decision-making. The main idea is to transform language interval variables into three element connection numbers matrix and build multi-attribute optimization function and language interval attribute weights interval numbers of three element connection numbers by optimizing the aggregation of the matrix. This thesis calculates the potential value and makes priority ranking by set pair analysis. Finally, examples are given to show the procedure and effectiveness of the method.

three element connection numbers；linguistic interval；information aggregate method

WANG Wanjun. Linguistic interval information aggregation method based on three element connection numbers.Computer Engineering and Applications, 2014, 50（17）：219-222.

A

TP301.6

10.3778/j.issn.1002-8331.1310-0021

甘肃省高等学校研究生导师科研项目（No.1215-04）；甘肃省教育厅科研项目（No.1113-01）；兰州文理学院科研能力提升计划骨干项目（No.2012GGTS01）。

王万军（1974—），男，副教授，CCF会员，主要研究方向为计算机智能信息处理技术。E-mail：wangwanjun1@163.com

2013-10-08

2013-12-23

1002-8331（2014）17-0219-04

CNKI网络优先出版：2014-01-23,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0021.htm l