基于Vague软集的TOPSIS方法及其应用研究

陈文，余本功

1.安庆师范学院计算机与信息学院，安徽安庆 246133

2.合肥工业大学管理学院，合肥 230009

基于Vague软集的TOPSIS方法及其应用研究

陈文1，余本功2

1.安庆师范学院计算机与信息学院，安徽安庆 246133

2.合肥工业大学管理学院，合肥 230009

运用传统的TOPSIS方法进行不确定型决策时存在一定的困难，而Vague软集是一种处理不确定信息的重要工具。为此，给出了一种加权的Vague软集间相似度计算方法并加以证明，在对传统的TOPSIS方法进行修正的基础上，将Vague软集理论应用于TOPSIS方法中，将修正后的TOPSIS方法应用于仓储中心选址问题中，结果表明，Vague软集能极大地提高TOPSIS方法在不确定型决策领域中的应用价值。

逼近于理想值的排序方法（TOPSIS）；Vague软集；相似度；不确定型决策

1 引言

TOPSIS[1]法，又称“逼近于理想值的排序方法”，它是Hwang和Yoon于1981年提出的一种适用于多属性问题的决策分析方法，其基本思路是确定最理想解和最不理想解，然后求出各方案与最理想解和最不理想解之间的加权欧氏距离，由此得出各方案的TOPSIS值，并将其作为评价方案优劣的标准。自产生到现在，TOPSIS法已成功应用于确定型决策问题中，但运用传统的TOPSIS方法进行不确定型决策时存在一定的困难，为此，一些专家和学者将Fuzzy集理论和Vague集理论应用于TOPSIS方法中，如梁昌勇等学者研究了一种基于TOPSIS的混合型多属性群决策方法[2]，胡辉、徐泽水等学者研究了基于TOPSIS的区间直觉模糊多属性决策法[3]，周珍等学者研究了基于Vague集多准则决策的模糊TOPSIS方法[4]，周晓光等学者研究了基于Vague集的TOPSIS方法及其应用[5]等，这些研究取得了一定的成果，但由于Fuzzy集理论和Vague集理论都有一个共同的不足之处，就是它们都只能处理一部分不确定信息，即参数工具理论的不充分[6]，为了解决这个问题，学者M olodtsov于1999年引入Vague软集[7]概念以克服这些不足，在此基础上，学者Qin K和Hong Z[8]将软集思想和Vague集现有理论结合起来并提出了Vague软集的一些基本概念，王昌等学者研究了Vague软集的性质及相似度计算方法[9]。但就目前看，将Vague软集理论引入TOPSIS方法的研究并不多见，为此，本文首先给出了一种加权的Vague软集间相似度计算方法并加以证明，在此基础上对传统的TOPSIS方法进行了修正，最后将基于Vague软集的修正TOPSIS方法应用于仓储中心选址决策问题中，结果表明基于Vague软集的修正TOPSIS方法是科学的、有效的。

2 Vague软集的定义

Vague软集理论是在Vague集理论的基础上发展起来的。

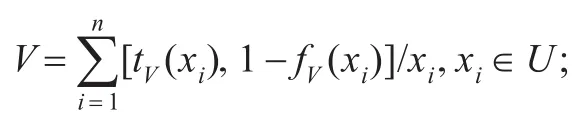
定义2[7]设U是一个论域，P(U)是U的幂集，E是一个参数集，V⊆E，且F:V→P(U)是一个映射，称(F，V)为U上的一个软集。

定义3[11]设U是一个论域，E是一个参数集，V⊆E，且F:V→V(U)是一个映射，即∀e∈V，F(e)是U上的一个Vague集，称(F，V)为U上的一个Vague软集，用VSS(U)来表示。

3 Vague软集的相似度

目前关于Vague集的相似度[12-14]的研究比较深入，但关于Vague软集的相似度的研究却不多见，王昌等学者曾给出一种Vague软集的相似度的定义[6]，但未考虑到参数的权重，为此，本文给出一种加权的Vague软集相似度定义。

Vague软集作为一种处理模糊信息的工具，真隶属度、假隶属度及犹豫度是它的三个主要特征，因此，认为Vague软集间相似度的计算公式应包含这三种信息。

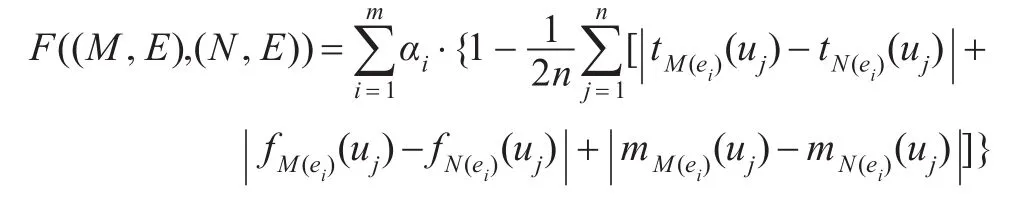
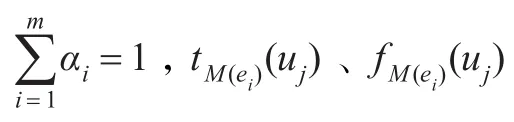
定义Vague软集的相似度之后，易证Vague软集的相似度F((M，E)，(N，E))满足以下5个条件：

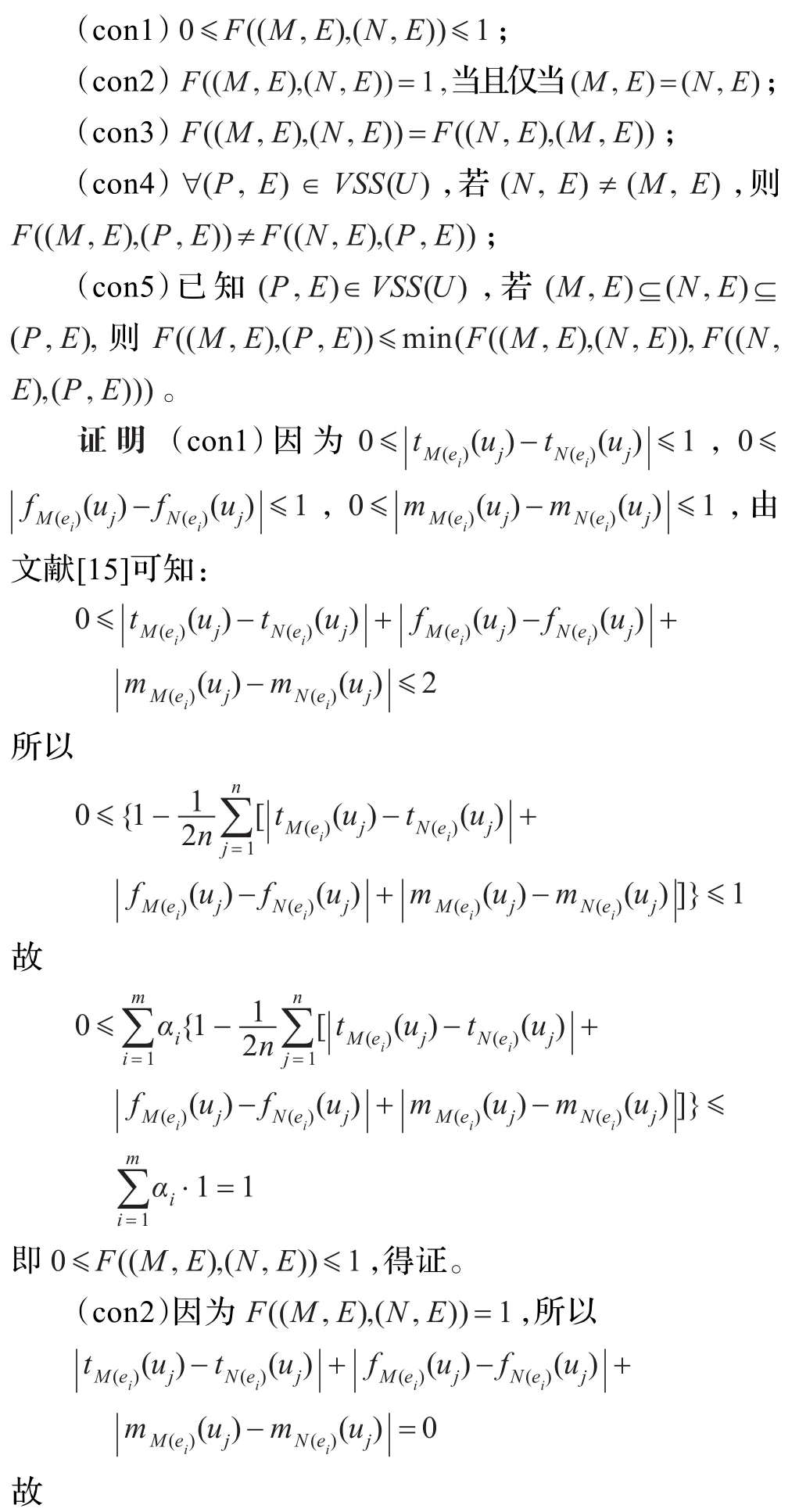
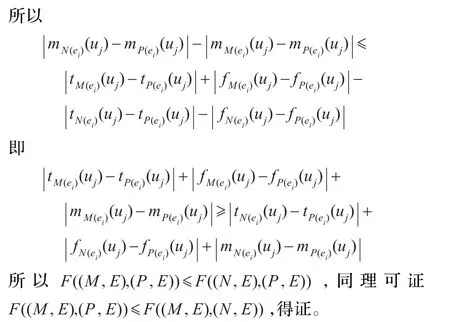
综上所证，函数F((M，E)，(N，E))严格满足上述5个条件，故运用它来计算软集间的相似度是合理的。实际应用中，如果软集(M，E)和软集(N，E)的相似度越高，则函数F((M，E)，(N，E))的值越接近于1；反之，函数F((M，E)，(N，E))的值越接近于0。

4 修正后的TOPSIS方法

TOPSIS是一种简单且合乎逻辑的多因素优选方法。TOPSIS方法的基本思想是：确定一个实际可能不存在的最佳方案和最差方案，然后计算每个实际备选方案与最佳方案和最差方案之间的距离（欧氏距离），最后利用理想解的相对接近度作为综合评估的标准。运用传统的TOPSIS方法进行不确定型决策时存在一定的困难，为此，引入Vague软集，并在以下两个方面对传统的TOPSIS方法进行了修正：首先运用相似度替代欧氏距离来衡量每个备选方案与最理想（最不理想）方案之间的相似度，这就克服了欧氏距离的片面性[16]。其次，从某种意义上说，相似度和欧氏距离是两个相反意义的概念，因此在计算每个具体方案的TOPSIS值时，计算公式的分子需修正为每个备选方案与最佳方案的相似度。修正后的TOPSIS方法的具体计算步骤如下：

（1）确定论域U={u1，u2，…，un}，参数集E={e1，e2，…，em}，及各备选方案在论域U上的软集(Ak，E)∈VSS(U)，k=1，2，…，h，表示共有h个方案。

（2）根据层次分析法和熵权法确定参数ei的综合权重αi。

（3）确定最理想方案的软集(M，E)∈VSS(U)和最不理想方案的软集(N，E)∈VSS(U)。

（4）计算每个备选方案(Ak，E)与最理想方案(M，E)及最不理想方案(N，E)间的相似度：

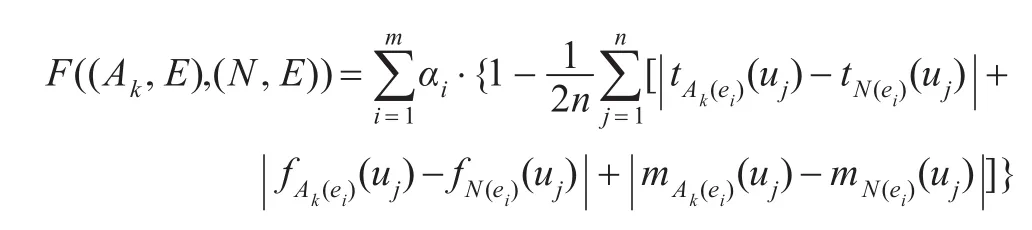
（5）计算每个备选方案(Ak，E)的TOPSIS评价值，并根据评价值对合作伙伴进行排序优选。

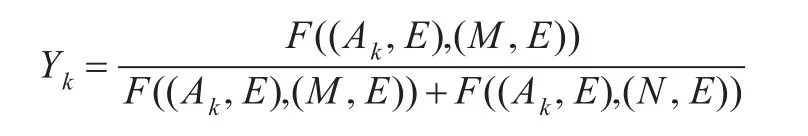
其中Yk的值越大，表明备选方案(Ak，E)越优。

5 修正后的TOPSIS方法在仓储中心选址中的应用研究

5.1 仓储中心选址的指标研究

经过详细调研，本文认为仓储中心的构建与运营一般分为3个阶段：物资输入、仓储中心建设和运营及物资输出，按照这种思路，在遵循评价指标体系设计原则的基础上，以某光彩大市场仓储中心选址为例，设计出仓储中心选址的指标体系，如图1所示。

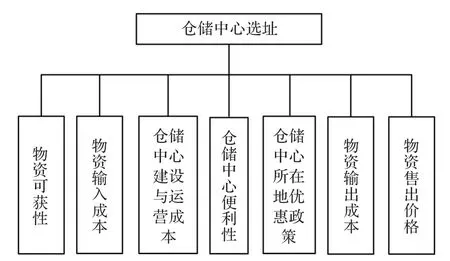
图1 仓储中心选址的指标体系

其中，物资可获性是指仓储中心获得物资的难易程度，仓储中心便利性是指仓储中心距离物资的供应市场及物资的消费市场是否便利，仓储中心所在地优惠政策是指仓储中心所在地政府在鼓励招商引资、税收等方面提供的优惠政策。该指标体系既简单实用，而且也能全面、科学地反映出仓储中心的优劣程度。

5.2 修正后的TOPSIS方法在仓储中心选址中的应用研究

由于生产经营的需要，某光彩大市场急需建立一个仓储中心，经过市场调研，有五个备选地址可供选择，本文简称为A1地、A2地、A3地、A4地和A5地。根据上述指标体系，通过专家反复论证，运用层次分析法和熵权法确定七个指标的综合权重分别为：（0.1，0.1，0.2，0.2，0.1，0.1，0.2），下面运用基于Vague软集的修正TOPSIS方法对该问题进行决策。

为了便于专家判断，设定论域U={支持，反对}= {u1，u2}，参数集E={物资可获性强，物资输入成本高，仓储中心建设与运营成本高，仓储中心便利性好，仓储中心所在地优惠政策多，物资输出成本高，物资售出价格高}={e1，e2，e3，e4，e5，e6，e7}，参数的权重αi依次为：α1= 0.1、α2=0.1、α3=0.2、α4=0.2、α5=0.1、α6=0.1、α7=0.2，准备工作就绪后，专家运用Vague软集对五个备选地址、最理想地址及最不理想地址进行评判，分别获得它们在论域U上的软集：(A1，E)、(A2，E)、(A3，E)、(A4，E)、(A5，E)、(M，E)及(N，E)，具体评价值如表1～7所示。

获得上述七个软集的评价值后，运用定义的软集间相似度函数分别计算每个备选地址(Ak，E)与最理想地址(M，E)及最不理想地址(N，E)间的相似度，并计算出每个备选地址(Ak，E)的TOPSIS评价值，结果如表8所示。以A1地为例，其TOPSIS值的计算过程如下：

表1 A1地的VSS（U）

表2 A2地的VSS（U）

表3 A3地的VSS（U）

表4 A4地的VSS（U）

表5 A5地的VSS（U）

表6 最理想地址的VSS（U）

表7 最不理想地址的VSS（U）

同理可求出F((A1，E)，(N，E))=0.275，所以A1地的TOPSIS值为：

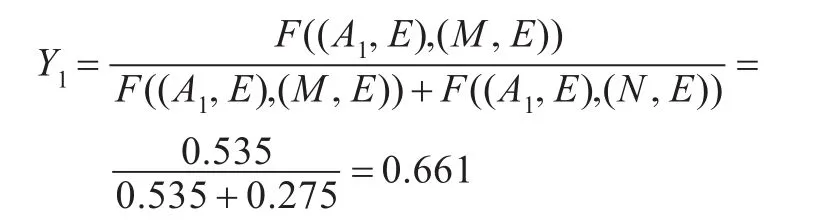
从表8可以看出，A4地的TOPSIS值最大，这表明A4地最优，实际应用过程中，该光彩大市场选定A4地作为仓储中心后，取得了预期的经济效益，很好地满足了市场的需求。

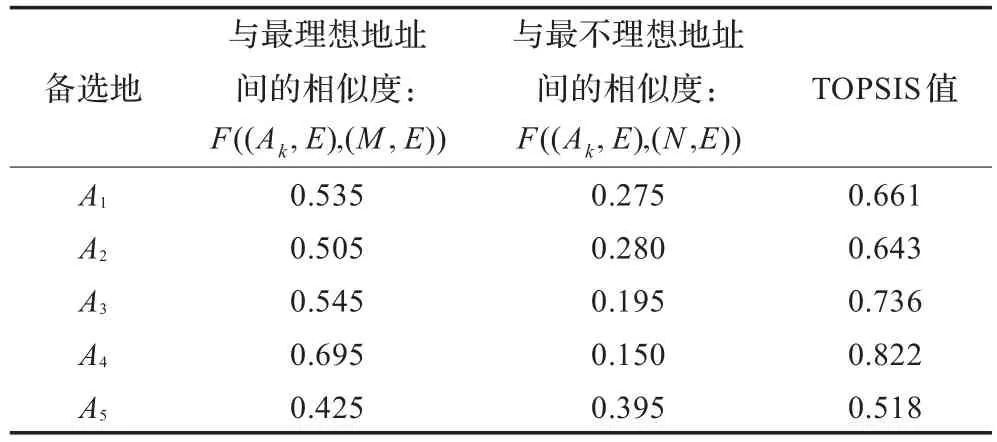
表8 五个备选地址的TOPSIS值

6 结束语

Vague软集理论作为Vague集理论的一种推广，它能提高参数工具理论的充分性，从而能够处理更多不确定信息。本文给出了一种加权的Vague软集间相似度定义，并在此基础上将Vague软集理论应用于TOPSIS方法中，以某仓储中心选址决策问题为例，验证了基于Vague软集的修正TOPSIS方法的实用性和可操作性，这为解决不确定型决策问题提供了一种新方法，但由于Vague软集理论本身还需完善和发展，因此如何更好地将Vague软集理论应用于决策中，还需进一步深入研究。

[1]霍佳震.物流与供应链管理[M].北京：高等教育出版社，2006：280-282.

[2]梁昌勇，戚筱雯.一种基于TOPSIS的混合型多属性群决策方法[J].中国管理科学，2012，20（4）：109-117.

[3]胡辉，徐泽水.基于TOPSIS的区间直觉模糊多属性决策法[J].模糊系统与数学，2007，21（5）：108-112.

[4]周珍.基于Vague集多准则决策的模糊TOPSIS方法[J].数学的实践与认识，2006，36（2）：278-283.

[5]周晓光.基于Vague集的TOPSIS方法及其应用[J].系统工程理论方法应用，2005，14（6）：537-541.

[6]王昌.Vague软集的相似度量及其应用[J].统计与决策，2012（2）：77-79.

[7]Molodtsov D.Soft set theory-first results[J].Computer and Mathematics with Applications，1999，37（4）：19-31.

[8]Qin K，Hong Z.On soft equality[J].Journal of Computational and Applied Mathematics，2010，234（5）：1347-1355.

[9]王昌，袁敏.Vague软集的一些代数性质[J].计算机工程与应用，2010，46（13）：15-22.

[10]Gau W L，Buehrer D J.Vague sets[J].IEEE Transactions on Systems Man and Cybernetics，1993，23（2）：610-614.

[11]Xu W，M a J，Wang S，et al.Vague soft sets and their properties[J].Computer and Mathematics with Applications，2010，59（2）:787-794.

[12]范平，梁家荣，李天志，等.Vague集之间相似度量的新方法[J].计算机工程与应用，2006，42（34）：70-72.

[13]张福金，王鸿绪.Vague集的相似度量及其应用[M].昆明：云南科技出版社，2010：2-120.

[14]Szm idt E，Kacprzyk J.Distances between intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，2000，114：505-518.

[15]黄国顺，刘云生.Vague集的三维表示及一组距离测度[J].计算机科学，2004，31（12）：117-129.

[16]杨懿，武昌，刘涵，等.基于改进TOPSIS法的维修保障系统效能评估研究[J].海军工程大学报，2006，18（6）：21-25.

CHEN Wen1,YU Bengong2

1.School of Computer and Information, Anqing Teachers College, Anqing, Anhui 246133, China
2.School of Management, Hefei University of Technology, Hefei 230009, China

There exist some difficulties if the traditional TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）is used for uncertain decision-making problem, and the Vague soft set is an important tool of processing uncertain information. For this reason, a weighted resemblance degree of the Vague soft set is defined and proved in the paper,then the paper modifies the traditional TOPSIS by applying the Vague soft set theory. The modified TOPSIS method is used for the decision of warehousing center location problem , and the data of the results indicate that the Vague soft set theory can greatly improve the application value of the TOPSIS method in uncertain decision-making problem.

Technique for Order Preference by Similarity to Ideal Solution（TOPSIS）; Vague soft set; resemblance degree;uncertain decision-making

CHEN Wen, YU Bengong. Theory and application study on modified TOPSIS method based on Vague soft set.Computer Engineering and Applications, 2014, 50（17）：214-218.

A

TP391

10.3778/j.issn.1002-8331.1301-0041

国家自然科学基金（No.70631003）；安徽省高校省级优秀青年人才基金项目（No.2012SQRW 079）；教育部人文社科规划基金项目（No.12YJA 630176）。

陈文（1985—），男，讲师，主要研究领域为信息管理与信息系统、决策科学；余本功（1971—），男，博士，副教授，研究领域为信息管理与信息系统、决策科学。E-mail：royalty509@126.com

2013-01-07

2013-02-06

1002-8331（2014）17-0214-05

CNKI网络优先出版：2013-02-20,http://www.cnki.net/kcms/detail/11.2127.TP.20130220.1554.002.htm l