高斯粒子群优化粒子滤波检测前跟踪算法

汲清波，耿丽群，任超

哈尔滨工程大学信息与通信工程学院，哈尔滨 150001

高斯粒子群优化粒子滤波检测前跟踪算法

汲清波，耿丽群，任超

哈尔滨工程大学信息与通信工程学院，哈尔滨 150001

针对低信噪比时标准粒子滤波对弱小目标的检测与跟踪时存在的粒子贫乏、跟踪精度对粒子数目要求高等问题，提出一种基于高斯粒子群优化粒子滤波的弱小目标检测前跟踪算法。利用高斯粒子群优化算法优化重采样后的粒子集，使粒子集朝着后验概率密度分布取值较大的区域运动，增加粒子的多样性，克服了粒子贫乏问题，并在保证跟踪精度的前提下降低了跟踪所需要的粒子数目，提高了标准粒子滤波算法的检测和跟踪性能。同时，建立了检测前跟踪系统的观测模型和系统模型，对基于标准粒子滤波检测前跟踪算法和优化算法进行仿真，仿真实验结果表明高斯粒子群优化粒子滤波的检测前跟踪算法相比基于标准粒子滤波的检测前跟踪算法具有更好的检测与跟踪性能。

弱小目标；检测前跟踪；高斯粒子群优化算法；粒子滤波算法

1 引言

检测前跟踪技术广泛应用于红外弱小目标的检测与跟踪领域[1-3]，基于递推贝叶斯估计的检测前跟踪（TBD）方法为解决低信噪比下的弱小目标的检测与跟踪提供了一条有效途径。粒子滤波（PF）算法作为最优贝叶斯估计的一种数值实现方法在检测前跟踪技术领域中的应用受到国内外学者的广泛关注[4-5]。

标准粒子滤波算法在应用于低信噪比弱小目标的检测前跟踪时虽能取得很好的效果，但存在着粒子退化、粒子多样性降低等问题严重影响目标检测概率和检测精度。因此很多学者提出改进算法，文献[6]提出一种基于修正Hough变换和粒子滤波相结合的TBD算法，通过修正Hough变换估计出目标航迹作为先验信息，然后利用粒子权重值构造似然比检测目标。文献[7]提出的高斯粒子滤波器（GPF）算法避免了粒子滤波重采样，提高了计算效率，但是算法估计性能下降。文献[8]提出基于遗传进化思想的新遗传粒子滤波算法，将快速M etropolis-Hastings移动作为遗传算法的交叉和变异算子，利用遗传算法代替重采样。

本文将高斯粒子群优化算法应用到标准粒子滤波算法中，提出一种基于高斯粒子群优化粒子滤波的弱小目标检测前跟踪方法（PSOPFTBD），利用粒子群优化算法优化重采样后的粒子集，使得粒子采样集朝着后验概率密度分布取值较大的区域运动，从而克服了粒子贫乏问题并且在保证跟踪精度的前提下降低了跟踪所需要的粒子数目，提高了标准粒子滤波的检测和跟踪性能。

2 高斯粒子群优化粒子滤波算法及实现

2.1 粒子滤波算法中存在的问题

标准粒子滤波算法中选取系统状态变量的转移概率密度函数为重要性密度函数，但由于重要性密度函数没有考虑最新观测的数据，从重要性函数抽取的粒子样本与真实的后验分布产生的样本存在较大的偏差，特别是当量测数据出现在转移概率密度函数的尾部或者似然函数与转移概率密度函数相比过于集中呈尖峰时，造成系统偏差较大，重要性权重的方差随着时间而随机递增[9]，使得粒子的权重集中到少数粒子上，经过几步递归后，可能只有一个粒子的权值非零，其他粒子的权值很小，造成粒子退化现象[10]。

为了克服粒子退化现象，引入重采样阶段，重采样过程就是要消除那些权值小的粒子，并复制权值大的粒子。尽管重采样在一定程度上解决了退化问题，但由于重采样是根据粒子的权值大小对粒子进行采样复制，这样权值较大的粒子被多次复制，权值小的粒子被消除，粒子丧失了多样性，甚至经过若干次迭代后，所有粒子都坍塌到一个点上引起粒子样本枯竭，造成了粒子贫乏问题。

标准粒子滤波在系统初始状态未知时，要保证估计精度，需要的粒子数目较大，如果粒子数目较小，就会出现没有粒子分布在真实状态附近的情况，经过迭代后会丢失目标，严重影响系统的跟踪精度。

2.2 粒子群算法

粒子群优化算法（Particle Swarm optimization，PSO）是由Kennedy和Eberhart于1995年提出的一种有效的全局寻优算法[11]。PSO算法是基于群体智能理论的优化算法，它通过群体中粒子间的合作和竞争产生的群体智能信息指导优化搜索。PSO算法中粒子群的每个粒子代表跟踪定位问题的目标的一个可能位置，每个粒子具有位置和速度两维特征。算法首先初始化一群随机粒子，定义适应度函数，然后迭代寻找最优解。在每一次迭代过程中利用个体极值pj即粒子通过一次迭代后更新得到的个体最优解，其中j=1，2，…，n，n为最大迭代次数。全局极值gj即整个粒子群中的全局最优解其中j=1，2，…，n，n为最大迭代次数。按下面的速度更新公式和位置更新公式来更新每个粒子。使得每个粒子向全局极值gj移动，改善粒子群所携带的位置信息。

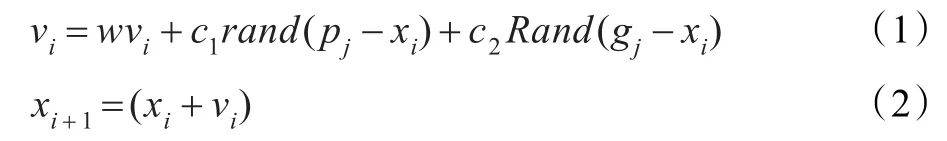
其中，rand和Rand均是介于(0，1)区间的随机数，w为惯性系数，c1和c2是正的常数，代表粒子向个体极值和全局极值移动的权重即加速常数，xi为初始粒子群状态，vi为速度更新量。粒子群优化算法自从提出后受到广泛的关注，很多改进算法相继提出[12-14]，在检测前跟踪算法中由于惯性系数w、移动权重c1和c2、粒子群算法的最大速度vmax等参数很难确定，因此选择高斯粒子群优化算法优化粒子滤波算法，高斯粒子群优化算法[15]是由K rohling在2004年提出的改进算法，算法用高斯分布按如下公式更新速度信息和位置信息，唯一需要确定的参数只有粒子数目。

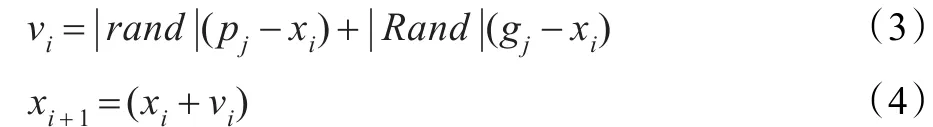
高斯粒子群算法通过速度更新和位置更新，使每个粒子向全局极值移动，提高整个粒子群的性能，提高后续的检测和跟踪性能。

2.3 高斯粒子群优化粒子滤波算法

高斯粒子群优化算法和粒子滤波算法都是通过更新初始粒子群中粒子所携带的信息来不断地更新自身的位置，来获得目标真实位置的最优估计。因此可以利用高斯粒子群优化算法改进标准粒子滤波方法的性能，将两种算法进行有效的结合并应用到检测前跟踪算法中得到基于高斯粒子群优化粒子滤波的检测前跟踪算法（PSOPFTBD）。在PSOPFTBD算法中选择粒子的权值函数作为高斯粒子群优化算法的适应度函数，通过选择第j次迭代过程中权值最大的粒子作为全局极值gj，在第j次迭代过程中第i个状态为存在的粒子的状态标定为个体极值pji(i=1，2，…，nmax)，其中nmax为粒子数目，通过如下速度更新公式和位置更新公式使权值低的粒子向适应度值高的粒子移动改善粒子的多样性，同时提高跟踪性能。

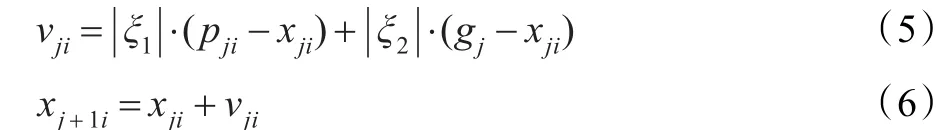
其中ξ1和ξ1是均值为0方差为1的复高斯随机变量，j为高斯粒子群算法迭代次数，vji为第j次迭代过程中第i个粒子的速度更新量，pji为第j次迭代过程中第i个粒子的个体最优解，gj为第j次迭代过程中整个粒子群中的全局最优解。xji和xj+1i分别为第j次迭代及第j+1次迭代后第i个粒子的状态，因此PSOPFTBD算法的具体步骤如下：

步骤1初始化。

k=0时，粒子初始化：由先验概率p(x0)产生粒子群，所有粒子的权值为1 N。

步骤2序贯重要性采样（SIS），k=1，2，…，T。

（1）抽取粒子：

（2）计算每个粒子的重要权值：

（3）权值归一化：

步骤3重采样。

步骤4高斯粒子群优化算法优化粒子群。

（1）设定迭代次数n=5。

（2）确定粒子的权值函数为适应度函数。

（3）确定全局极值gj和个体极值pj。

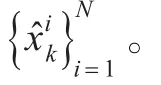
（5）寻找当前时刻权值最大的粒子更新适应度函数值、个体极值和全局极值。

步骤5输出阶段。

输出一组粒子，得到当前时间的后验均值估计：

步骤6令k=k+1，当下一帧测量到来时，转到步骤2。

2.4 弱小目标的检测前跟踪算法的数学模型

2.4.1 弱小目标检测前跟踪的系统模型

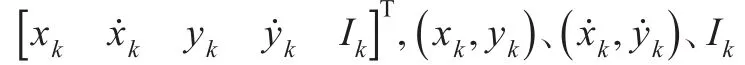
其中，F为系统转移矩阵如式（12）所示，vk是均值为零的高斯白噪声，其协方差矩阵为Q如式（13）所示。

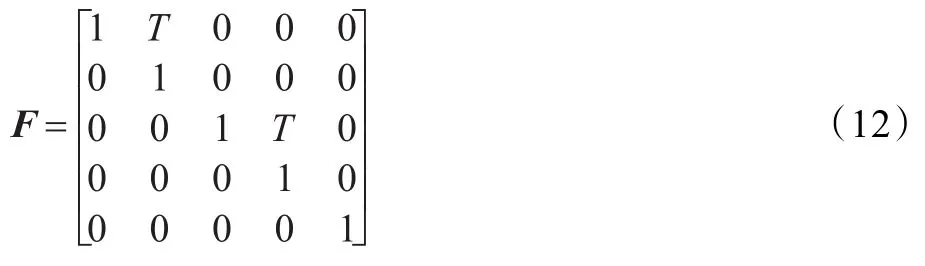
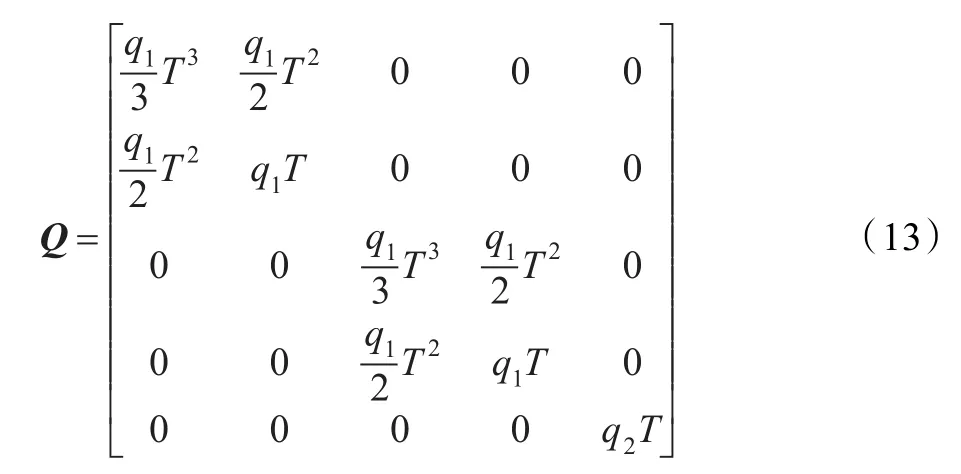
式（13）中，q1、q2分别代表目标运动中的过程噪声和目标强度噪声的大小。

2.4.2 弱小目标检测前跟踪的量测模型

把通过成像仪获得的前k帧图像当成量测，用Zk表示，设zk表示第k帧图像，则前k次量测为Zk= {z1，z2，…，zk}。假设成像仪的成像平面大小N像素× M像素，当用大小为∆x×∆y的分辨单元对成像所成像进行扫描时，那么在k时刻，每个分辨单元(i，j)(1≤i≤N，1≤j≤M)都会记录一个量测z：

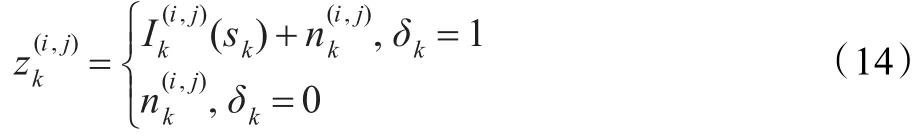
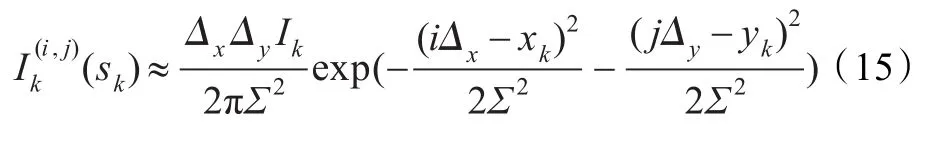
3 仿真结果分析

在系统模型（11）中的过程噪声q1、目标强度噪声q2分别取0.001和0.01。图1为低信噪比情况下观测数据序列中的6帧灰度图像。目标在第12、17、22帧图像中存在，但从图1的灰度图像中不能获得目标的任何有用信息。

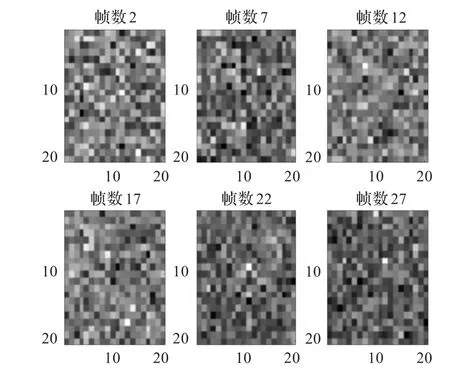
图1 观测数据序列中的6帧灰度图像

粒子滤波器的参数如下：粒子数4 000；转移概率pb=pd=0.05；初始时刻目标出现的概率为μ1=0.05；阈值γ=2；目标出现的似然比阈值为Λt=1.5。

从图2中可以看出利用PSOPFTBD算法产生的预测轨迹能够准确地跟踪目标的实际运动轨迹。

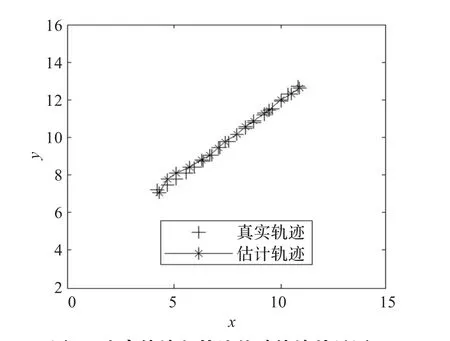
图2 真实轨迹与算法估计轨迹效果图

下面进行PSOPFTBD算法和PFTBD算法的对比实验，即两种算法在同一较低信噪比前提下，但不同粒子数目条件下的检测概率和跟踪误差的对比，以及在同一粒子数目前提下，但不同信噪比情况下检测概率和跟踪误差的比较，通过每帧图像检测概率的平均值和均方根误差的平均值来衡量两种算法的检测和跟踪性能。

3.1 不同粒子数目下的对比结果

在信噪比为2.2，粒子数分别为4 000，2 000，1 000，500的情况下，进行了100次Monte Carlo仿真，目标从第7帧开始出现，在第23帧消失，种算法在粒子数目极低的情况下每帧图像的检测概率平均值和均方跟误差的平均值曲线如图3所示。

由图3（a）可以看出从第7帧目标出现开始，PSOPFTBD算法的检测概率明显高于PFTBD算法。第11帧开始到第22帧结束PSOPFTBD算法的平均检测概率大于0.6，而PFTBD算法的平均检测概率低于0.6。

由图3（b）可知，两种算法的均方误差随着帧数的递增逐渐下降，同时，PSOPFTBD算法的均方根误差明显小于PFTBD算法，且均方跟误差曲线收敛速度比PFTBD算法的收敛速度快。

从表1中可以看出两种算法的检测概率随着粒子数的增加逐渐升高，而在粒子数目相同的情况下PSOPFTBD的检测概率明显高于PFTBD，实验结果表明改进算法在粒子数目相同的前提下提高了目标的检测概率。

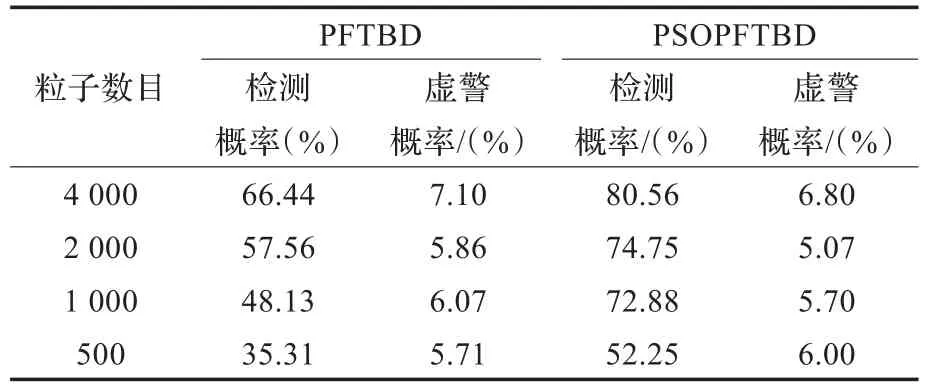
表1 不同粒子数目下两种算法检测性能的比较

从表2中可以看出两种算法的均方根误差随着粒子数目的增多而减小，而在粒子数目相同的情况下PSOPFTBD算法的均方根误差的平均值小于PFTBD算法的均方根误差的平均值，实验结果表明PSOPFTBD算法在粒子数目相同的情况下具有更高的跟踪精度。

表2 不同粒子数目下的两种算法跟踪性能的比较

3.2 不同信噪比下的对比结果

在粒子数为4 000，信噪比分别为1.4、2.2，3.0的情况下，进行了100次蒙特卡罗仿真，对两种算的检测性能和跟踪性能进行比较。

从图4（a）两种算法检测性能对比图可以看出从第7帧目标出现开始PSOPFTBD算法每一帧的检测概率都要高于PFTBD算法的检测概率，检测性能明显好于PFTBD算法的检测性能。

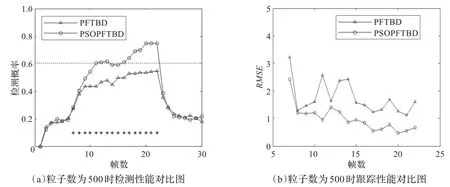
图3 粒子数为500时两种算法的检测性能和跟踪性能的对比图

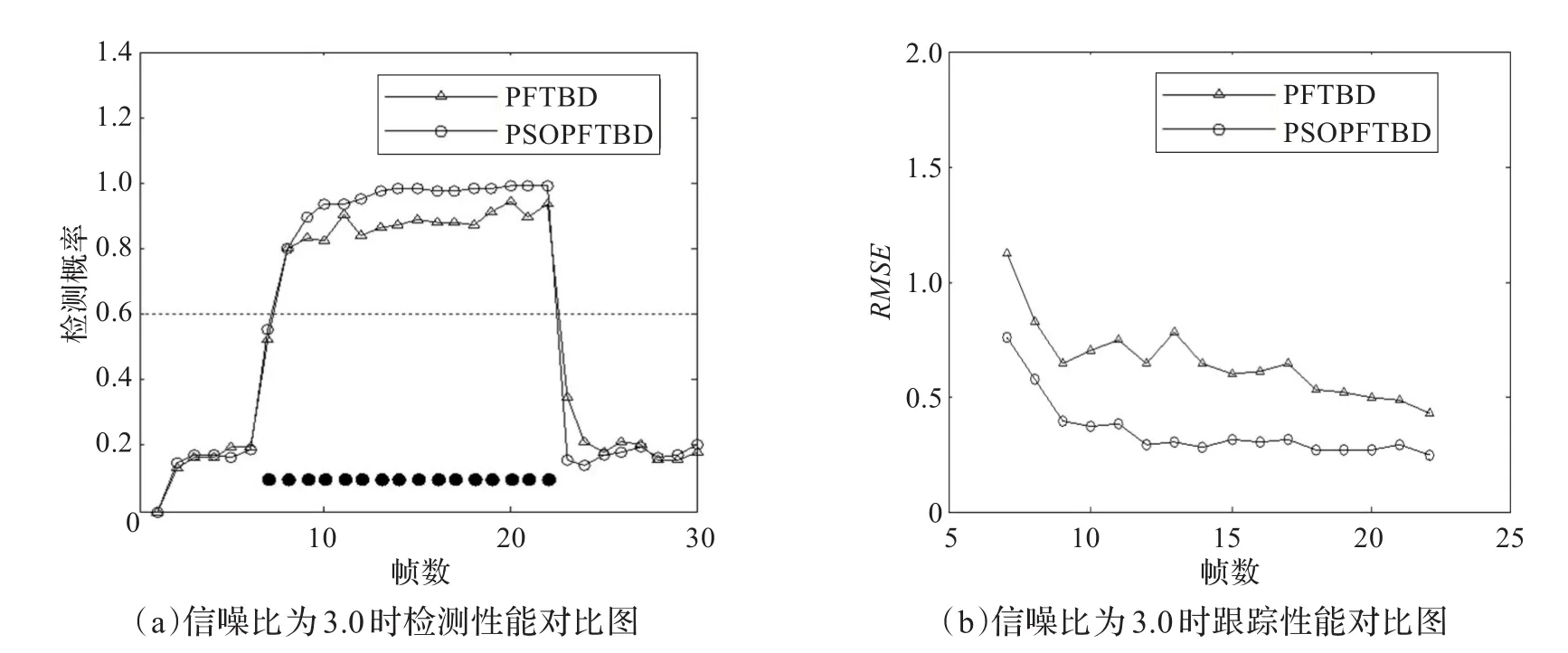
图4 信噪比为3.0时两种算法的检测性能和跟踪性能的对比图

同样由图4（b）两种算法跟踪性能对比图可以看出在信噪比为3时PSOPFTBD算法的均方根误差的平均值小于PFTBD算法的均方根误差平均值。

从表3可以得出两种算法的检测概率随信噪比的升高而增加，在信噪比为3.0时PSOPFTBD算法的检测概率最高达到92.56%。在信噪比相同的情况下PSOPFTBD算法的检测概率高于PFTBD算法，虚警概率低于PFTBD算法。

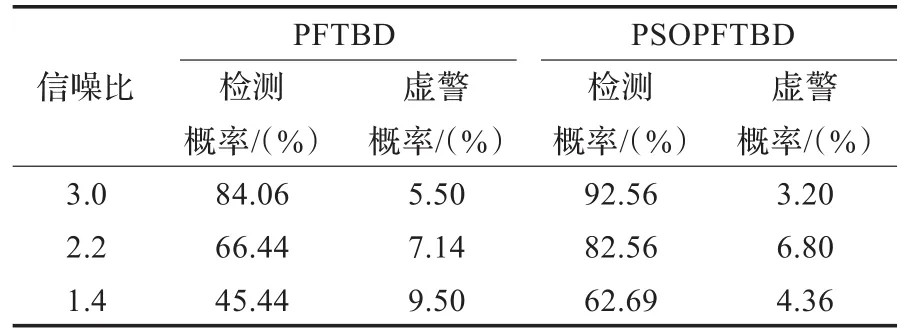
表3 不同信噪比下的两种算法的检测性能比较

从表4可以得出两种算法的均方根误差的平均值随信噪比的升高而降低，在信噪比相同的情况下PSOPFTBD算法的均方根误差的平均值明显小于PFTBD算法，提高了跟踪精度。

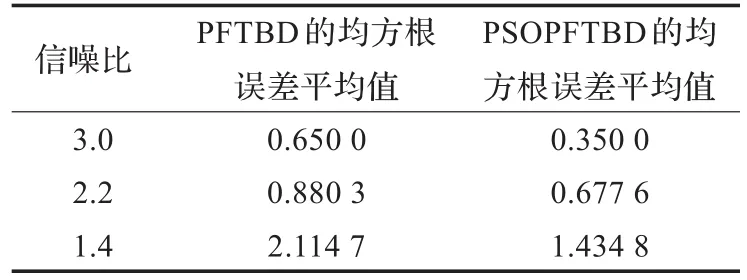
表4 不同信噪比下的两种算法的跟踪性能比较

3.3 算法复杂度分析

由以上实验结果可知PSOPFTBD算法的检测性能和跟踪性能明显优于PFTBD算法，但是由于PSOPFTBD算法是在标准粒子滤波算法中引入了高斯粒子群优化算法，增加了算法的复杂程度，降低了算法的实时性。然而可以根据不同精度场合要求，通过减少粒子数量或者可通过对程序的优化来改善PSOPFTBD算法的实时性缩短算法执行时间。还可进一步研究选择好的重要性密度函数来改善PSOPFTBD算法的实时性。

4 结束语

将高斯粒子群优化算法应用到粒子滤波算法中，提出了PSOPFTBD算法。该算法通过高斯粒子群优化使采样粒子集朝着后验概率密度分布取值较大的区域运动克服了粒子贫乏、跟踪精度对粒子数目要求高等问题。仿真实验结果表明PSOPFTBD算法的性能优于PFTBD算法，提高了在低信噪比和粒子数目较少条件下的检测和跟踪性能。

[1]Blostein S D，Huang T S.Detection of small moving objects in image sequences using multistage hypothesis testing[J].IEEE Trans on Signal Processing，1991，39（7）：1611-1629.

[2]Fan Lina，Wang Jinkuan，Yan Dongmei，et al.Target detection using radar with dynamic programming approach[C]//The International Conference on Control，Automation and Systems Engineering，CASE09.Piscataway：IEEE，2009：442-445.

[3]Li Tao，Wu Siliang，Zeng Haibin，et al.A new radar trackbefore-detect algorithm based on dynamic programming[J].Acta Electronica Sinica，2008，36（9）：1824-1828.

[4]Boers Y，Driessen H.Patricle filter based track before detect algorithms[C]//Proceedings of the SPIE.Bellingham：SPIE，2003：20-30.

[5]Samond D J，Birch H.A particle filter for track-beforedetect[C]//IEEE Proceedings of the American Control Conference，Washington，2001：3755-3760.

[6]樊玲，张晓玲.雷达微弱目标探测的改进检测前跟踪算法[J].电子科技大学学报，2011，40（6）：839-843.

[7]Kotecha J H，Djuric P A.Gaussian particle filtering[J].IEEE Trans on Signal Process，2003，51（10）：2592-2601.

[8]李翠云，姬红兵.新遗传粒子滤波的红外弱小目标检测跟踪与检测[J].西安电子科技大学学报：自然科学版，2009，36（4）：619-624.

[9]Kong A，Liu J S，Wong W H.Sequential imputations and Bayesian m issing data problems[J].Journal of the American Statistical Association，1994，89（425）：278-288.

[10]Crisan D，Doucet A.A surevy of convergence results on particle filtering methods for practitioners[J].IEEE Transactions on Signal Processing，2002，50（3）：736-746.

[11]Kennedy J，Eberhart R.Particle swarm optimization[C]// Proc of the IEEE Int Conf on Neural networks.Piscataway：IEEE Service Center，1995：1941-1948.

[12]Lim K S，Buyam in S，Ahmad A，et al.An improved leader guidance in multi objective particle swarm optimization[C]//Proc of 6th Asia International Conference on Mathematical modelling and Computer Simulation，2012：34-39.

[13]Britto A，Pozo A.Using archiving methods to control convergence and diversity for many-objective problem s in particle sw arm optimization[C]//2012 IEEE Congress on Evolutionary Computation，2012.

[14]Peng Hu，Li Rong，Cao Lianglin，et al.Mutiple swarms multi-objective particle swarm optimization based on decomposition[J].Procedia Engineering，2011：3371-3375.

[15]K rohiling R A.Gaussian swarm：a novel particle swarm optimization algorithm[C]//Proc of the IEEE Conf on Cybernetics and Intelligent System s，2004：372-376.

JI Qingbo,GENG Liqun,REN Chao

College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China

Considering the particle impoverishment and the large particle sample size for the high tracking accuracy in dim target track before detect algorithm based on standard particle filter（PFTBD）, a dim target track before detect algorithm based on Gaussian particle swarm optimization particle filter（PSOPFTBD）is proposed. Gaussian particle swarm optimization algorithm is applied to optimize the particles after resampling, which makes the particles move towards the larger values of posterior density function. The PSOPFTBD algorithm increases the diversity of the particles, overcomes the particle impoverishment, and the particle sample size for accurate state estimation is also reduced. As a result, the detection and tracking performance is improved. The PSOPFTBD algorithm is tested on a tracking and detection mathematical model, and the results are compared with the results of the standard PFTBD algorithm. The simulation results show that the PSOPFTBD algorithm outperforms the PFTBD algorithm.

dim target;track before detect;Gaussian particle swarm optimization;particle filter

JI Qingbo, GENG Liqun, REN Chao. Track before detect algorithm based on Gaussian particle swarm optimization particle filter. Computer Engineering and Applications, 2014, 50（17）：205-209.

A

TP391

10.3778/j.issn.1002-8331.1211-0015

汲清波（1975—），女，博士研究生，副教授，研究领域为图像处理、目标检测识别与跟踪技术等；耿丽群（1987—），男，硕士研究生，研究方向为非线性信号与图像处理；任超（1987—），男，硕士研究生，研究方向为非线性信号与图像处理。E-mail：gengliqun@hrbeu.edu.cn

2012-11-01

2013-01-25

1002-8331（2014）17-0205-05

CNKI网络优先出版：2013-07-15,http://www.cnki.net/kcms/detail/11.2127.TP.20130715.1411.012.htm l