基于SVD和TKEO的轴承振动信号特征提取

李葵，范玉刚，吴建德

1.昆明理工大学信息工程与自动化学院，昆明 650500

2.云南省矿物管道输送工程技术研究中心，昆明 650500

基于SVD和TKEO的轴承振动信号特征提取

李葵，范玉刚，吴建德

1.昆明理工大学信息工程与自动化学院，昆明 650500

2.云南省矿物管道输送工程技术研究中心，昆明 650500

为了解决滚动轴承振动信号中微弱故障信息难以提取的问题，提出了一种基于奇异值分解（Singular Value Decomposition，SVD）和Teager-Kaiser能量算子（Teager-Kaiser Energy Operator，TKEO）的轴承振动信号特征提取方法。采用SVD将突变信息从背景噪声和光滑信号中分离，提取信号的突变信息；利用TKEO计算突变信息的瞬时能量，对该能量信号进行频谱分析，从而提取出轴承振动信号的能量频谱特征，用于故障检测。将该方法应用于轴承外圈、内圈局部故障状态下的振动信号特征提取，利用特征信息能够准确检测并识别出故障类型，表明了该方法的可行性和有效性。

奇异值分解；Teager能量算子；故障诊断

在机械故障诊断领域内，滚动轴承是机械设备中最为常见、也是最容易损坏的元件之一。研究表明，滚动轴承故障90%由轴承元件表面的局部损伤造成，如外圈、内圈、滚动体表面的点蚀、裂纹和剥落等[1]。当发生这些损伤时，滚动体高速旋转经过这些损伤处就会受到周期性的冲击，在振动中产生周期性突变信号，这些突变信号包含有丰富的故障信息，能够准确地反映轴承故障引起的撞击、振荡、转速改变和结构变形与断裂等故障。因而，检测突变信号是监视滚动轴承运行状态的有效途径，通过提取突变信号的特征进行故障诊断仍然是目前的研究热点。

奇异值分解（SVD）能够在强噪声背景下清晰有效地检测突变信息，在故障诊断领域已有许多成功应用的案例，但大多数案例将SVD应用于降噪滤波[1-3]或进行奇异谱分析[4-5]，在提取突变信息的特征方面缺乏相应的研究。利用SVD在噪声背景下进行特征信息分离和弱信号提取方面具有零相移、波形失真小、信噪比高等优点，本文将SVD与非线性信号处理领域中的Teager-Kaiser能量算子（TKEO）[6-9]理论相结合，提出了一种基于SVD和TKEO理论的轴承故障诊断方法。该方法利用SVD从背景噪声和光滑信号中分离出突变信息，并采用TKEO计算突变信息的瞬时能量，对该能量信号进行频谱分析，提取轴承振动信号的能量频谱特征，用于故障检测。

通过将该方法应用于实际工业背景的轴承故障检测中，成功地从强噪声振动信号中提取出轴承故障的突变信号，诊断出轴承外圈、内圈的局部故障，且精度很高，证明了该方法的可行性和有效性。

1 SVD提取突变信息理论

SVD是指[1]：对于一个实矩阵A∈Rm×n，不管其行列是否相关，必定存在正交矩阵U=[u1u2…um]∈Rm×m和V=[v1v2…vn]∈Rn×n，使得：

成立，其中S=[diag(σ1，σ2，…，σk)O]或者其转置，这取决于m＜n还是m＞n，S∈Rm×n，O为零矩阵，k=m in(m，n)，且有σ1≥σ2≥…≥σk≥0，称为矩阵A的奇异值。

1.1 构建吸引子轨迹矩阵

将SVD应用于信号处理的关键是利用信号构造出合适的矩阵。利用一维信号构造矩阵，一般有两种方法，一种是利用信号构建一个吸引子矩阵[10]，即Hankel矩阵，另一种是通过对信号的连续截断来构造矩阵[11-12]。矩阵构造方式不同，则SVD的信号处理效果就不一样[13]。当采用Hankel矩阵构建吸引子矩阵时，SVD可以有效去除复杂信号中的噪声成分，且能降低光滑信号的影响。因此，为了在强噪声背景下提取有效的故障突变信号，本文采用构造Hankel矩阵进行奇异值分解。

假设具有某故障的机械系统测试信号为X= [x1，x2，…，xN]，利用此信号可以构造Hankel矩阵如下：

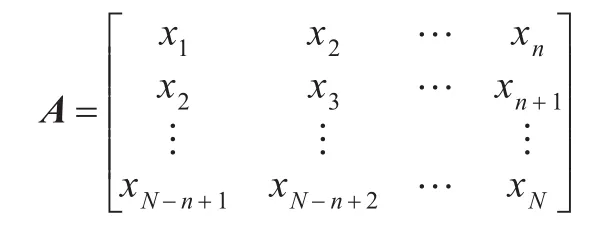
其中1＜n＜N。令m=N-n+1，则A∈Rm×n。

1.2 突变信息特征提取

为了利用SVD实现信号的分解，将式（1）改写成用列向量ui和vi表示为：

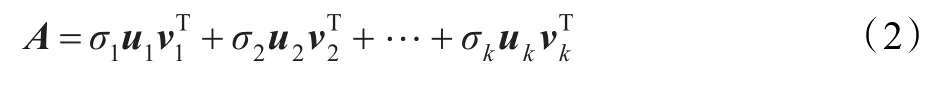
根据SVD逆运算进行重构，以往文献大都将矩阵A表示成：A=D+W，本文为了提取突变信息，可将其表示成：A=D+Q+W，其中D是光滑信号对应的轨迹矩阵，W是噪声对应的轨迹矩阵，Q是突变信号对应的轨迹矩阵。

研究表明，虽然不同光滑信号的秩可能不同，但光滑信号对应的重构轨迹矩阵是奇异的（即其秩kD＜k），奇异值随着k增大迅速衰减。对于突变信号对应的重构轨迹矩阵，由于其突变性，必定是比光滑信号秩要高的矩阵，即它的秩kQ(kD＜kQ＜k)，且随着k的增大，奇异值下降过程有一个过渡阶段。同样，由于噪声的随机性，其构成的轨迹矩阵是列（行）满秩矩阵，且奇异值大小几乎相等。

通过上述理论可知，D、Q和W的各自奇异值分解后奇异值的分布具有不同的规律。因此可以推断，光滑信号、突变信息和噪声对构造矩阵A分解后的各奇异值的贡献也不一样：即D主要贡献0～kD阶，Q主要贡献0～kQ阶，而噪声对各阶的贡献几乎相等。因此，可以选择某个（或某些）奇异值σk(kD＜k＜kQ)，其他奇异值置零，利用SVD逆过程得到Q，再进行反空间变换。根据Hankel矩阵的特点，使用简便法选择Q的第一行和最后一列构成剔除光滑信号和噪声后的突变信号[14]。

需要指出的是，该方法不要求突变信息具有周期性，也适合非周期突变信息检测。

2 瞬时能量提取

TKEO是由Kaiser提出的一种非线性算子，它能有效提取信号的瞬时能量，对信号瞬时变化具有良好的时间分辨率，近年来被学者广泛应用于求取信号的瞬时频率和瞬时幅值，并取得了很好的效果[6-9]。

在连续时间信号x(t)中，TKEO定义为[7]：

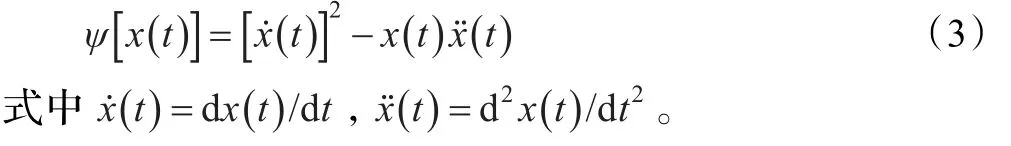
与连续信号相对应，用离散差分方程代替连续时间量的导数，便可得到离散信号x(n)的TKEO定义为：

可见，对于离散时间信号TKEO只需要三个样本点即可计算任意点n处的信号源能量，因此，它对于信号的瞬时变化具有良好的时间分辨率，能够高精度地检测信号中的瞬态成分。实际上，TKEO输出追踪产生信号所需的总能量，即可以表达振动信号的瞬时能量值。

设时变振动信号为：

构造对称差分信号[15]：

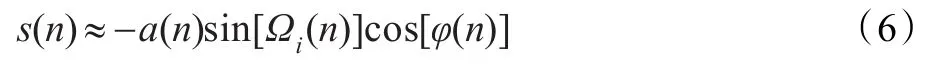
3 基于SVD和TKEO理论的轴承故障诊断方法

由上分析，本文提出基于SVD和TKEO理论的轴承故障诊断方法，采用SVD从背景噪声和光滑信号中分离突变信息，提取滚动轴承的微弱周期性故障信号，并利用TKEO理论求取瞬时能量信号，对该能量信号进行Fourier变换，得到Teager能量频谱，获取频率成分，进行故障检测。

具体步骤如下：

（1）对原始一维故障信号X构造m×n维hankel矩阵A。

（2）对A采用SVD求取奇异值矩阵S，得到奇异值分布状态。

（3）根据1.2节中理论选择奇异值分布曲线中缓慢过渡阶段对应的某个（或某几个）奇异值利用SVD逆运算重构信号，并进行反空间变换获得突变信号。

（4）根据TKEO理论求取突变信号的瞬时Teager能量。

（5）对瞬时Teager能量进行Fourier变换，得到Teager能量频谱，获取频率成分。

（6）根据Teager能量频谱特征得出诊断结论。

4 实验研究

4.1 实验说明

用上述原理和方法对实际轴承故障诊断中常见的外圈、内圈故障信号进行分析。数据来自美国凯斯西储大学电气工程实验室。

实验采用6205-2RS JEM SKF型轴承，轴承参数见表1。在不影响轴承正常使用性能情况下，用电火花机在滚动轴承外圈和内圈上各加工制作直径为0.177 8 mm，深0.279 4 mm的小槽模拟轴承外圈、内圈局部裂纹故障，轴承负载2.237 kW，转频1 730 r/m in，采样频率为48 kHz，采样长度为4 800点。

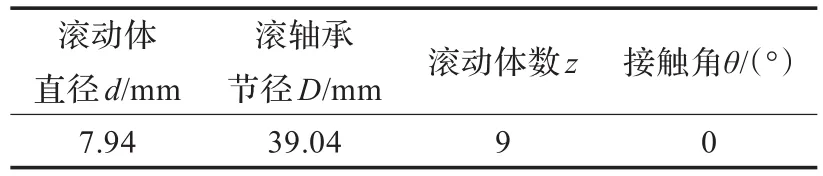
表1 6205-2RS JEM SKF型轴承参数

根据轴承振动理论，当外圈、内圈滚道存在损伤时，冲击发生的基频可计算为：

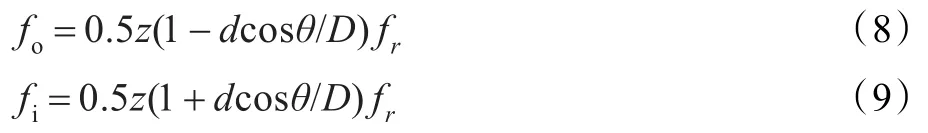
计算得轴承外圈故障基频fo=103.36 Hz，内圈故障基频fi=156.14 Hz。

对实验特征频率求误差计算方法为：

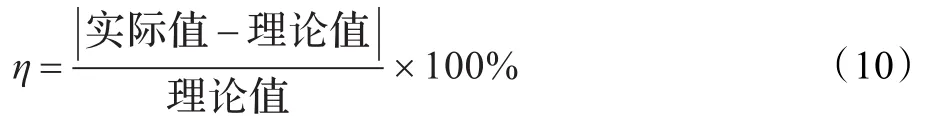
由实验条件可知频率分辨率为5.86 Hz，则可得外圈故障理想误差为5.7%，内圈故障理想误差为3.8%。

4.2 信号分析

滚动轴承的振动信号由安装在轴承座上的传感器检测。轴承外圈固定，与轴承座直接配合，它和传感器之间的位置相对固定，故外圈故障产生的冲击特征在振动测试信号中比较明显，容易诊断。而滚动轴承内圈直接和转轴相连，随着转轴旋转，传感器和内圈故障点之间的相对位置随之变化，只有在内圈故障点通过轴承负荷区时，才会在振动信号中出现明显的冲击特征。另外，内圈故障引起的冲击经过滚动体、保持架、外圈和轴承座以及中间界面的传递之后，能量衰减损耗较大。因此，内圈故障振动信号中的冲击特征不明显，内圈故障诊断相对较难。

图1（a）为轴承外圈存在故障时的时域波形和奇异值分布图。图中可以看出，当滚动轴承外圈表面存在局部故障点时，时域波形出现了冲击特征，但并不明显；从奇异值分布图上可知奇异值缓慢过渡阶段为k=10～20，故本文取k=15进行信号重构。图1（b）为重构信号和瞬时Teager能量波形，可见重构信号很好地提取了微弱冲击信号，瞬时Teager能量波形突出了冲击特征，使得周期性冲击特征变得更加明显。从图1（c）Teager能量频谱和表2可见，冲击信号的基频是105.5 Hz，除此之外，还能够明显分辨出轴承发生故障时与此基频相对应的倍频，且倍频阶次连续，高达13阶，故障特征更加明显直观。根据4.1节中轴承振动理论计算的外圈故障冲击基频(fo=103.36 Hz)可准确判断为外圈发生故障（η= 2.1%，在理想误差以内）。

图2为轴承内圈故障诊断结果，从Teager能量频谱中获得峰值频率如表2所示，其基频152.3 Hz与理论计算的内圈故障冲击基频(fi=156.14 Hz)非常接近（η= 2.5%，在理想误差以内），同时提取到倍频阶次达12阶，在误差允许范围内可判断为轴承内圈出现故障。

上述根据本文提出的基于SVD和TKEO理论的轴承故障诊断方法得到的分析结果和实验真实情况完全吻合。

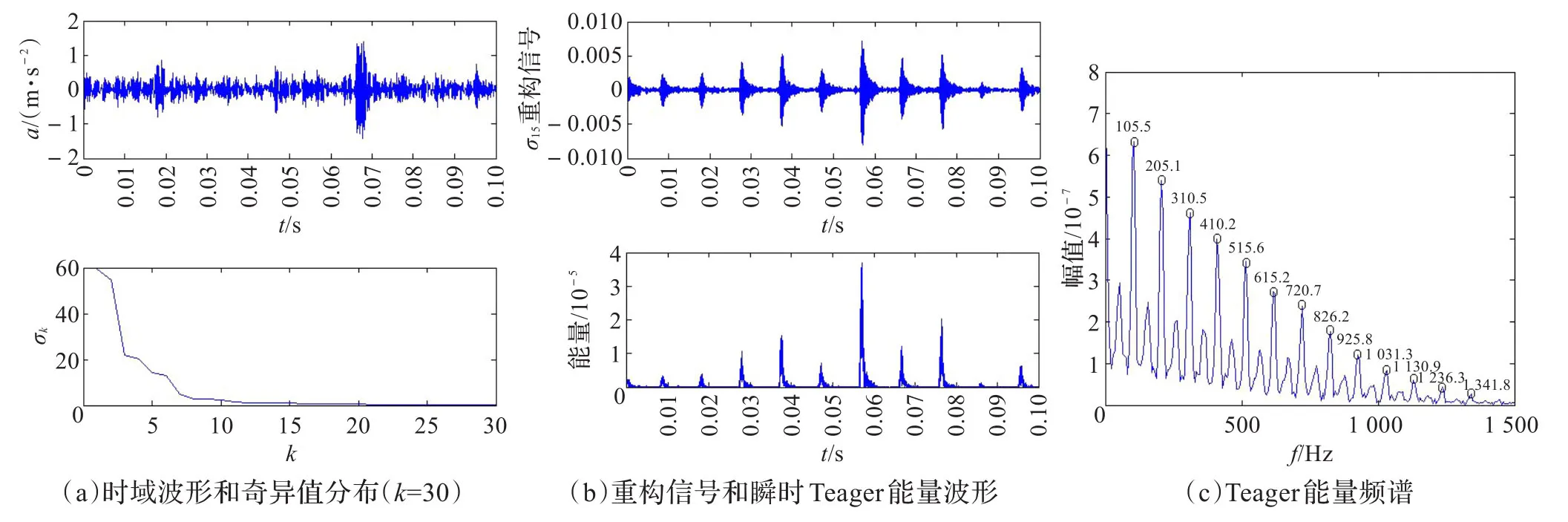
图1 轴承外圈故障信号分析结果

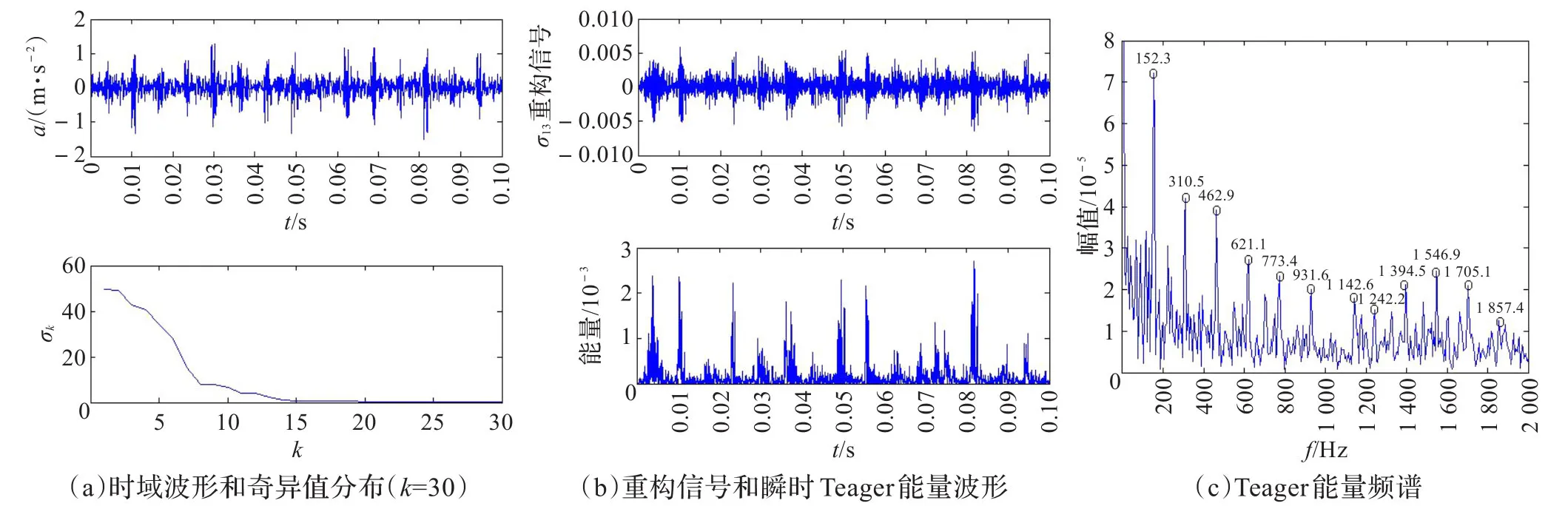
图2 轴承内圈故障诊断结果

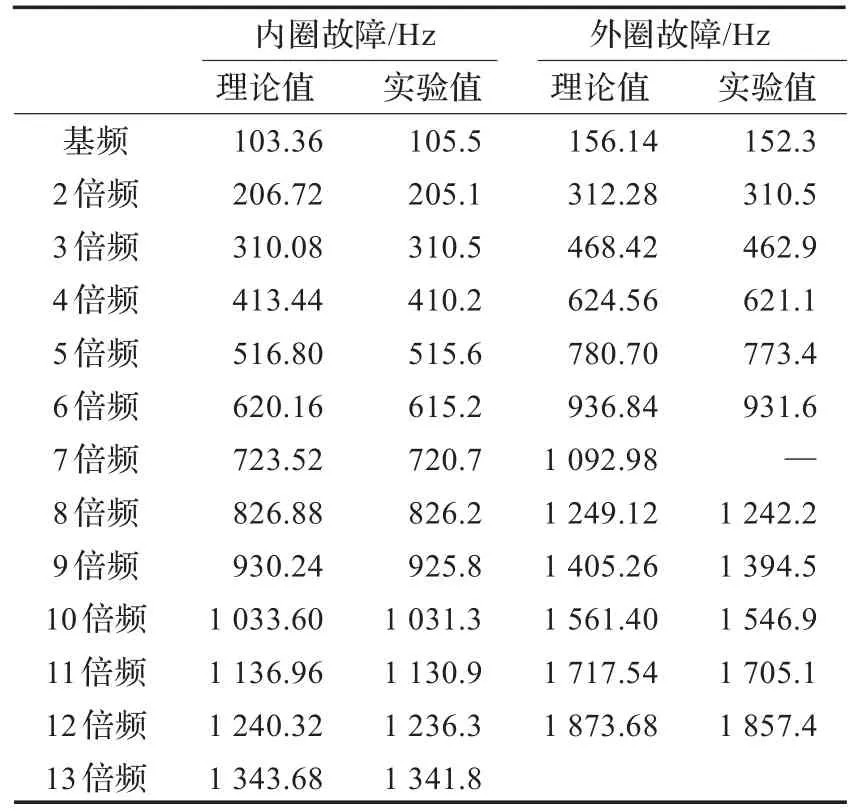
表2 冲击信号频率成分

将文献[1]中采用SVD提取特征信息的方法应用于本文实验，与本文结果进行对比。为了方便对比，按照文献[1]中SVD对信号去噪后进行Hilbert包络谱处理，得到幅值谱如图3所示，可以明显看到较为严重的噪声和半频干扰，相比于图1（c）和图2（c）有明显不足。

由此表明，本文方法能有效地抑制在滚动轴承故障诊断时出现的无法解释的半频干扰，并且精度很高。这表明本文所提方法在轴承故障诊断时更加有效。

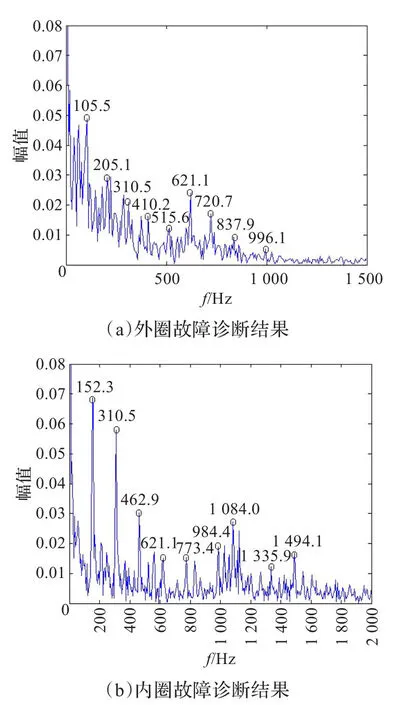
图3 文献[1]方法对轴承故障诊断结果

5 结论

（1）奇异值分解和重构能够在强噪声背景下有效降低信号中光滑信号和噪声的影响，从而能够更加清晰有效地检测并提取突变信息。

（2）Teager能量算子对于信号瞬时变化具有良好的时间分辨率，突出了冲击特征，使得周期性冲击特征更加明显。

（3）基于SVD和TKEO理论的轴承故障诊断方法可获得清晰的轴承故障特征基频及其倍频，能够有效地检测轴承故障。此外，该方法能很好地抑制半频干扰。

实验证明，采用本文提出的方法对轴承进行故障检测，可以有效分离并提取轴承振动信号中的故障特征，为轴承故障检测提供了一个有效途径。

[1]赵学智，叶邦彦，林颖.奇异值分解对轴承振动信号中调幅特征信息的提取[J].北京理工大学学报，2011，31（5）：572-577.

[2]陈恩利，张玺，申永军，等.基于SVD降噪和盲信号分离的滚动轴承故障诊断[J].振动与冲击，2012，31（23）：185-190.

[3]胡谋法，董文娟，王书宏，等.奇异值分解带通滤波背景抑制和去噪[J].电子学报，2008，36（1）：111-116.

[4]赵学智，叶邦彦，陈统坚.基于奇异值曲率谱的有效奇异值选择[J].华南理工大学学报：自然科学版，2010，38（6）：11-18.

[5]张超，陈建军，杨立东，等.奇异值熵和支持向量机的齿轮故障诊断[J].振动、测试与诊断，2011，31（5）：600-604.

[6]任达千，杨世锡，吴昭同，等.信号瞬时频直接计算法与Hilbert变换及Teager能量法比[J].机械工程学报，2013，49（9）：42-48.

[7]Kamath C.A new approach to detect congestive heart failure using Teager energy nonlinear scatter plot of R-R interval series[J].Medical Engineering & Physics，2012，34（7）：841-848.

[8]Erdamar A，Duman F，Yetkin S.A wavelet and Teager energy operator based method for automatic detection of K-complex in sleep EEG[J].Expert Systems with Applications， 2012，39（1）：1284-1290.

[9]张德祥，汪萍，吴小培，等.基于经验模式分解和Teager能量谱的齿轮箱故障诊断[J].振动与冲击，2010，29（7）：109-111.

[10]赵学智，陈统坚，叶邦彦.基于SVD的奇异性信号检测原理及其应用[J].振动与冲击，2008，27（6）：11-14.

[11]Liu Hongxing，Li Jian，Zhao Ying.Improved singular value decomposition technique for detecting and extracting periodic impulse component in a vibration signal[J]. Chinese Journal of Mechanical Engineering：English Edition，2004，17（3）：340-345.

[12]赵学智，叶邦彦，陈统坚.基于奇异值分解的铣削力信号处理与铣床状态信息分离[J].机械工程学报，2007，43（6）：169-174.

[13]Akritas A G，Malaschonokb G I.Applications of Singular Value Decomposition（SVD）[J].Mathematics and Computers in Simulation，2004，67（1）：15-31.

[14]赵学智，叶邦彦.分量形成方式对奇异值分解信号处理效果的影响[J].上海交通大学学报，2011，45（3）：368-374.

[15]Maragos P，Kaiser J F，Quatieri T F.Energy separation in signal modulations with application to speech analysis[J].IEEE Transactions on Signal Processing，1993，41（10）：3024-3051.

LI Kui, FAN Yugang, WU Jiande

1.Faculty of Information Engineering & Automation, Kunming University of Science and Technology, Kunming 650500, China
2.Engineering Research Center for Mineral Pipeline Transportation, YN, Kunming 650500, China

In order to solve the difficult problem in extracting the weak fault information from rolling bearing vibration signal, a method of feature extraction of bearing vibration signal based on Singular Value Decomposition（SVD）and Teager- Kaiser Energy Operator（TKEO）is proposed. The abrupt information is extracted from satin signal and noise by using the SVD. It calculates the instantaneous energy of abrupt information by using TKEO, and the energy information is analyzed to gain the feature of the energy frequency spectrum of bearing vibration signal that used for fault detection. The method is used to extract the fault feature of bearing vibration signal with outer and inner circle faults, and the fault type can be accurately detected and identified by feature information. The result shows that the method presented here is feasible and valid.

Singular Value Decomposition（SVD）; Teager-Kaiser Energy Operator（TKEO）; fault diagnosis

LI Kui, FAN Yugang, WU Jiande. Feature extraction of bearing vibration signal based on SVD and TKEO. ComputerEngineering and Applications, 2014, 50（17）：195-199.

A

TP274

10.3778/j.issn.1002-8331.1310-0111

国家自然科学基金（No.51169007）；云南省科技计划项目（No.2012CA 022，No.2011DA 005，No.2010DH004）；云南省中青年学术和技术带头人后备人才培养计划项目（No.2011CI017）。

李葵（1989—），男，硕士研究生，主要从事信号处理、机械故障诊断等研究；范玉刚（1973—），博士，副教授，从事基于机器学习的智能信息处理、数据挖掘技术研究等；吴建德（1979—），博士，教授，从事矿物管道输送实时检测与控制、工业过程数据分析与建模等研究。E-mail：likuigood@126.com

2013-10-14

2014-02-10

1002-8331（2014）17-0195-05

CNKI网络优先出版：2014-03-03,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0111.htm l