三次可展Bezier曲面的构造

顾春燕，林意

江南大学数字媒体学院，江苏无锡 214122

三次可展Bezier曲面的构造

顾春燕，林意

江南大学数字媒体学院，江苏无锡 214122

可展曲面在很多的工程领域里，尤其在机械工程设计中有着重要的作用，例如飞机机翼、汽车车身、船体、鞋和服装等的设计与制造等。在空间的一平面上分别生成2条3次Bezier曲线，该平面绕一固定轴旋转不同角度，生成两个相交的平面，这2条3次Bezier曲线跟随旋转，分别位于两相交平面上，并由这两条曲线生成直纹面。根据直纹面可展的充要条件，求解出未知的设计曲线和伴随曲线的控制顶点，最终生成3次可展Bezier曲面。

Bezier曲线；可展曲面；Bezier曲面；直纹面；控制顶点

1 引言

可展曲面在很多的工程领域里，尤其在机械工程设计中有着重要的作用，例如飞机机翼、汽车车身、船体、鞋和服装、管道等的设计与制造等，可用若干可展曲面片拼装而成。R.M.C.Bodduluri和B.Ravani[1]利用射影几何的方法构造可展曲面，由于这类可展曲面的控制顶点的几何含义不明显，所以不利于实际应用。J.Lang和O. Roschel[2]构造了一种(1，n)次有理Bezier可展曲面，由于过于简单，在实际应用中遇到很多困难。J.Hoschek[3]研究了可展曲面的一类插值及逼近问题，并对可展曲面的性质做了一些讨论，而它们的几何性质还需进一步研究。G.Aumann[4-6]在两个平行面上分别给出设计曲线，有设计曲线来设计可展曲面。根据直纹面是可展面的条件，得到关于两条设计曲线的导数和匹配函数之间的约束关系，再解出满足可展曲面的条件，但对两条曲线的限制非常严格，有时难以满足设计要求的可展曲面。Chu C.H和Sequin C.H[7]研究了二、三次Bezier可展曲面的条件和设计，并讨论了设计自由度。王树勋和叶正麟[8]利用de Casteljau算法提出了（2，3）次可展曲面的新设计方法，该方法易于控制曲面形状。孟雅琴[9]在G. Aumann[4-6]基础上扩展到更一般的情形，选取两个相交平面，由设计曲线和伴随曲线生成来构造可展曲面，此方法唯一的缺憾是存在特殊平面（如，XOZ面和YOZ面），在特殊平面上无法得到能生成可展曲面的设计曲线和伴随曲线。

本文将在文献[9]的基础上进行改进，利用绕固定轴旋转的方法生成两个相交平面，使得在所有面上都能得到生成可展曲面的设计曲线和伴随曲线。

2 3次可展Bezier曲面的设计

设两个平面π1和π2相交于直线L，不失一般性，建立空间直角坐标系，使Z轴在直线L上，平面π1和π2的方程为：

只有当方程组（9）的系数矩阵退化时，齐次方程组有非零解，即可以求出不全为零的设计曲线控制顶点的x分量。

当γ0=γ1-1时，解方程组（9）得：

由于式（9）和式（10）的系数矩阵与式（11）和式（12）的系数矩阵分别相同，且其秩均为3，故若要式（11）和式（12）有解，其增广矩阵的秩应为3，所以q0，q1，q2，q3应满足如下约束关系：

3 改进后的3次可展Bezier曲面的设计

由上述3次可展Bezier曲线的构造过程可知，当两个构造平面相交于Z轴时，设计平面和伴随平面是不能位于XOZ和YOZ平面的，因为XOZ平面的α=0，YOZ平面的α不存在。下面为解决此问题，提出了改进算法，让曲面的构造更加灵活。

设设计平面π1和伴随平面π2由XOZ面绕Z轴逆时针旋转θ1和θ2得到，θ1≠θ2，θ1，θ2∈[] 0，360°。

当θ1=0，θ2=90°时，式（17）即为：

当γ0=γ1-1时，设计曲线的控制顶点坐标的x，y分量如下（z分量不变）：

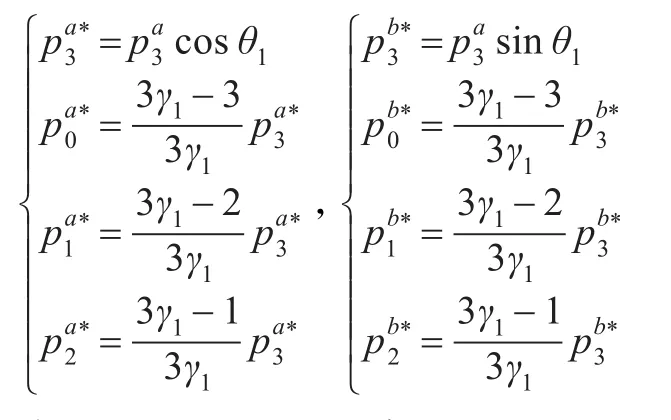
当β0=β1-1时，伴随曲线的控制顶点坐标的x，y分量如下（z分量不变）：

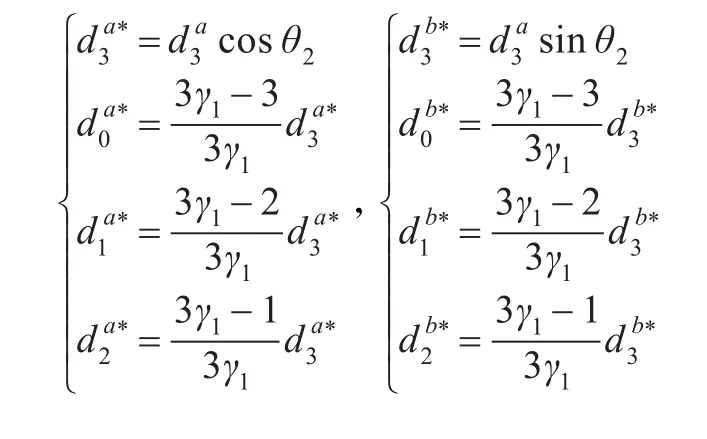
4 改进后3次可展Bezier曲面的构造实例

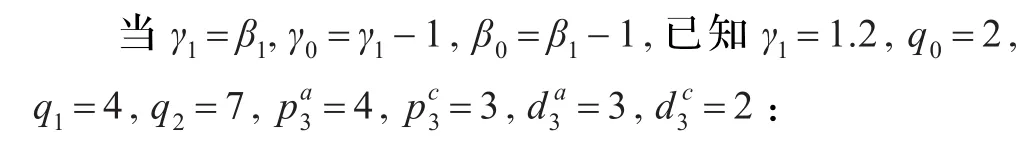
（1）θ1=0，θ2=40°时，可展曲面如图1所示。

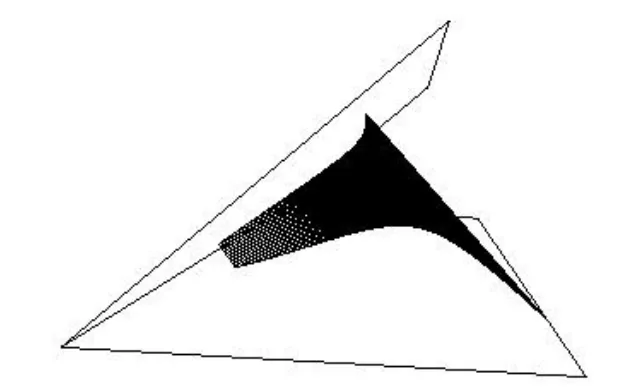
图1 θ1=0，θ2=40°时可展曲面

（2）θ1=0，θ2=90°时，可展曲面如图2所示。

（3）θ1=30°，θ2=100°时，可展曲面如图3所示。

（4）θ1=70°，θ2=180°时，可展曲面如图4所示。

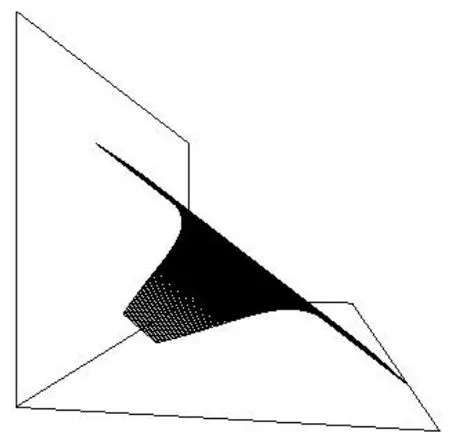
图2 θ1=0，θ2=90°时可展曲面

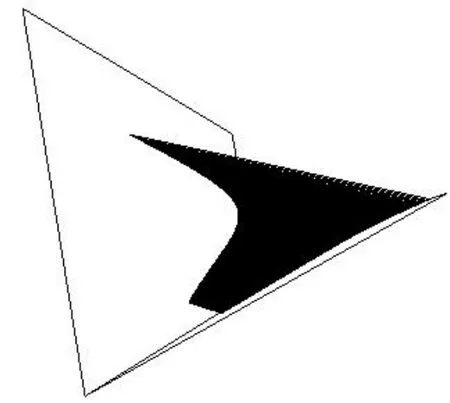
图3 θ1=30°，θ2=100°时可展曲面

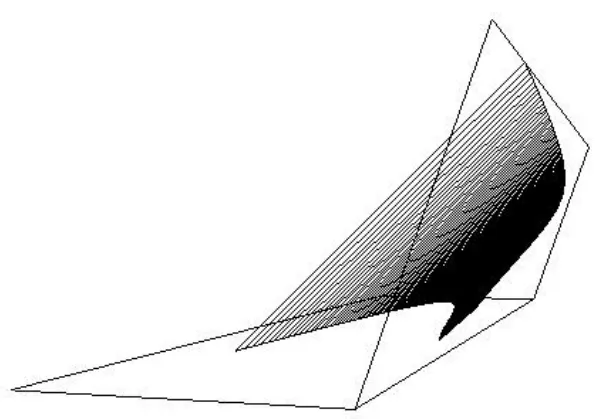
图4 θ1=70°，θ2=180°时可展曲面

5 结束语

本文在由文献[5]的基础上对可展Bezier曲面进行了改进，利用绕固定轴旋转的方法，使得平面的选取更加灵活自由，且此方法解决了α=0和α不存在时这两种情况下，设计曲线和伴随曲线不能生成的问题；相比较α，角度可以更直观地了解两平面的位置关系，在实际应用中更加简单方便，实用性较强。

[1]Bodduluri R M C，Ravani B.Design of developable surfaces using dualitybet ween plane and point geometries[J]. Computer Aided Design，1993，15（10）：621-632.

[2]Lang J，Roschel O.Developable（1，n）-Bezier surfaces[J]. Computer Aided Geometric Design，1992，9（4）：291-298.

[3]Hoschek J.Dual Bezier curves and surfaces[M]//Surfaces in computeraided geometric design.[S.l.]：North Holland，1983：147-156.

[4]Aumann G.Interpolation with developable Bezier patches[J]. Computer Aided Geometric Design，1991，8（5）：409-420.

[5]Aumann G.A simple algorithm for designing developable Bezier surfaces[J].Computer Aided Geometric Design，2003，20（8/9）：601-619.

[6]Aumann G.Degree elevation and developable Bezier surfaces[J].Computer Aided Geometric Design，2004，21（7）：661-670.

[7]Chu C H，Sequin C H.Developable Bezier patches：properties and design[J].Computer Aided Design，2002，34（7）：511-527.

[8]王树勋，叶正麟.基于直纹面的可展Bezier曲面的设计[J].计算机工程与应用，2008，44（17）：27-32.

[9]孟雅琴.可展曲面的构造与插值研究[M].上海：上海交通大学出版社，2010：45-64.

GU Chunyan,LIN Yi

College of Digital M edia,Jiangnan University,Wuxi,Jiangsu 214122,China

Developable surfaces have an important role in many engineering fields, especially in the design of mechanical engineering such as aircraft wing, auto body, hull, shoes and clothing. In the three-dimensional space, two cubic Bezier curves are generated in a plane. The plane rotates different angles by a fixed axis to generate two intersecting planes. The two cubic Bezier curves located on the two intersecting planes follow the plane rotating. Then, a ruled surface is generated.According to the necessary and sufficient conditions of developable ruled surface, the unknown control vertices of design curve and accompanied curve are calculated. Finally, developable cubic Bezier surfaces are generated.

Bezier curve; developable surfaces; Bezier surfaces; ruled surfaces; control points

GU Chunyan,LIN Yi.Design of developab le cubic Bezier sur faces.Computer Engineering and Applications,2014, 50（17）：169-172.

A

TP391

10.3778/j.issn.1002-8331.1210-0113

顾春燕（1988—），女，硕士研究生，研究方向：计算机辅助几何设计；林意（1963—），男，博士，副教授，研究生导师，研究方向：计算机辅助几何造型技术、计算机图形学。E-mail：337927012@qq.com

2012-10-12

2012-12-05

1002-8331（2014）17-0169-04

CNKI网络优先出版：2013-01-11,http://www.cnki.net/kcm s/detail/11.2127.TP.20130111.0951.010.htm l