基于BADV-Hop的传感器节点定位方法

谭爱平，陈浩，吴伯桥

1.湖南大学信息科学与工程学院，长沙 410082

2.湖南工业职业技术学院，长沙 410208

基于BADV-Hop的传感器节点定位方法

谭爱平1，2，陈浩1，吴伯桥1

1.湖南大学信息科学与工程学院，长沙 410082

2.湖南工业职业技术学院，长沙 410208

为了减少无线传感器网络节点的定位误差，提出蝙蝠算法（BA）和DV-Hop算法相融合的传感器节点定位方法（BA-DVHop）。在DVHop算法的第三阶段，利用蝙蝠算法代替最小二乘法来计算未知节点的坐标，以降低定位误差，对蝙蝠算法算法进行改进，避免算法陷入局部最优，最后在Matlab 2012平台上对算法性能进行仿真分析。相对于DV-Hop算法，BADV-Hop算法提高了传感器的节点定位精度，具有较高的应用价值，仿真结果验证了BA-DVHop的有效性。

无线传感器网络；蝙蝠优化算法；节点定位；DV-Hop算法

1 引言

节点定位技术是无线传感器网络（Wireless Sensor Network，WSN）的关键技术，在军事、环境监测和医疗卫生等领域有着广泛的应用前景，因此提高传感器节点精度成为WSN研究中的热点[1]。

由于WSN具有巨大的应用价值，因此，国内外专家和学者对其展开了一系列的研究，当前传感器节点定位算法分为：距离有关和距离无关的定位算法[2]。距离有关定位算法由于受到外界环境因素的干扰比较大，所以获得的误差较大，且成本高[3]；距离无关定位算法主要有质心算法、DV-Hop算法，这类定位算法无需额外硬件支持，功耗低，成为当前主要研究方向[4-5]。DV-Hop算法实现比较简单，只需要少量的锚节点就可以实现对未知节点的定位，备受关注，但是精度有待提高[6]。为此，学者们提出一些改进的DV-Hop算法，如文献[7]将RSSI策略引入到DV-Hop算法节点距离计算中，减小节点间误差，提高定位精度；文献[8]在DV-Hop算法中引入介质访问机制来调节距离误差；文献[9]通过引入最佳调整因子对每个锚节点计算的距离进行修正，从而减小了平均跳距的计算误差。采用遗传算法、模拟退火算法、蛙跳算法、粒子群算法等群智能算法对DV-Hop算法的误差进行校正，一定程度上提高了DV-Hop算法的定位精度[9-11]。蝙蝠算法（BA）是一种群智能优化算法，在准确性和有效性方面相较其他算法有很大优势，且没有许多参数要调整，为DV-Hop算法误差校正提供了一种新的研究思路[12]。

为了减少无线传感器网络节点的定位误差，提出一种改进蝙蝠算法（BA）和DV-Hop算法相融合的传感器节点定位方法（BA-DVHop）。在DV-Hop算法的第三阶段，利用蝙蝠算法代替最小二乘法来计算未知节点的坐标，并对蝙蝠算法进行改进避免算法陷入局部最优，最后在Matlab 2012平台上对算法性能进行仿真分析。仿真结果表明，BADV-hop定位算法在不同锚节点密度、不同通信半径、不同节点数量以及定位精确度等方面表现出良好性能。

2 DV-Hop定位算法及误差分析

2.1 DV-Hop定位算法工作步骤

第一阶段：计算节点的最小跳数。信标节点向网络发送一个广播信号，邻居节点接收到信号后，记录信标节点的坐标信息，并保存每个信标节点的最小跳数，然后向其他的邻居传感器节点传播，通过该方法，WSN网络中全部节点可以得到信标节点的位置信息和与信标节点间的跳数。

第二阶段：估算到信标节点的跳段距离。通过第一阶段后，每个信标节点就可以得到其他信标节点的坐标值和跳数，然后通过式（1）计算平均每跳距离，同时将每跳平均距离广播至网络中，未知节点将平均每跳距离值与最小跳数值相乘，得到其与信标节点间的距离：

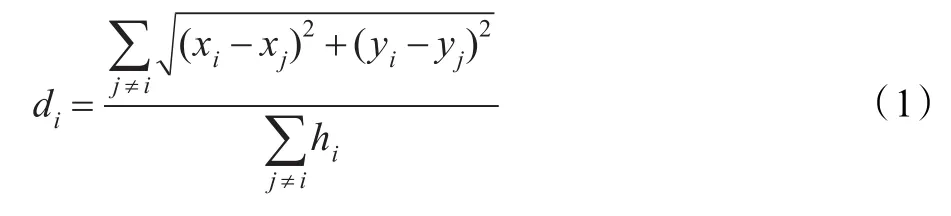
式中，hi是信标节点i和j之间的跳数，(xi，yi)、(xj，yj)是信标节点i，j的坐标。

第三阶段：通过最大似然法计算自身位置。设P1(x1，y1)，P2(x2，y2)，…，Pn(xn，yn)表示n个信标节点的坐标位置，待定位节点位置为(x，y)，其与信标节点估计距离分别为d1，d2，…，dn-1，可以建立式（2）的方程：

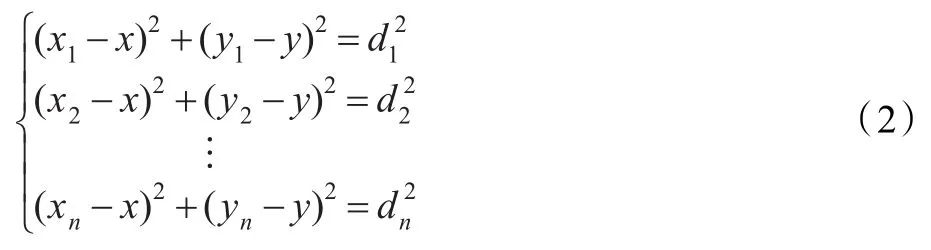
第一个方程组减去第后一个方程后，得到：

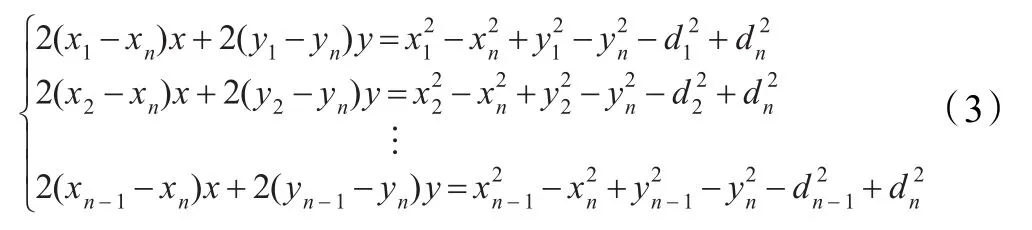
用线性方程组表示为AL=b，其中：

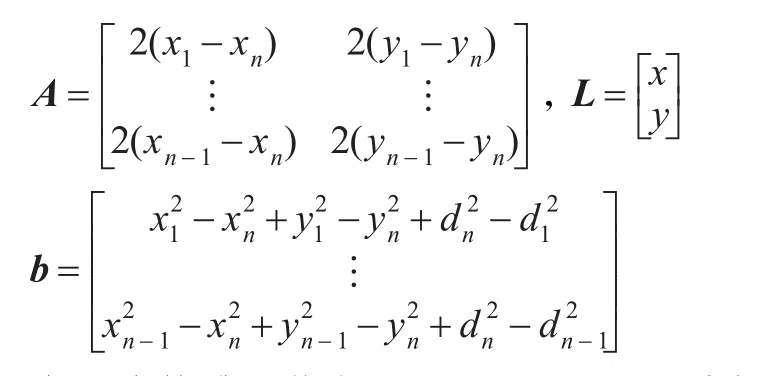
在无线传感器节点测距过程中，不可避免会产生一些随机误差，这样线性方程组为AL+N=b，N为误差向量，最小二乘法的求解方程为：

2.2 DV-Hop定位误差分析

设信标节点(xi，yi)，i=1，2，…，n，与未知节点(x，y)的实际距离为ri，i=1，2，…，n，测距误差为εi，那么|ri-di|＜εi，i=1，2，…，n。根据式（2）可知，(x，y)应该满足如下约束条件：

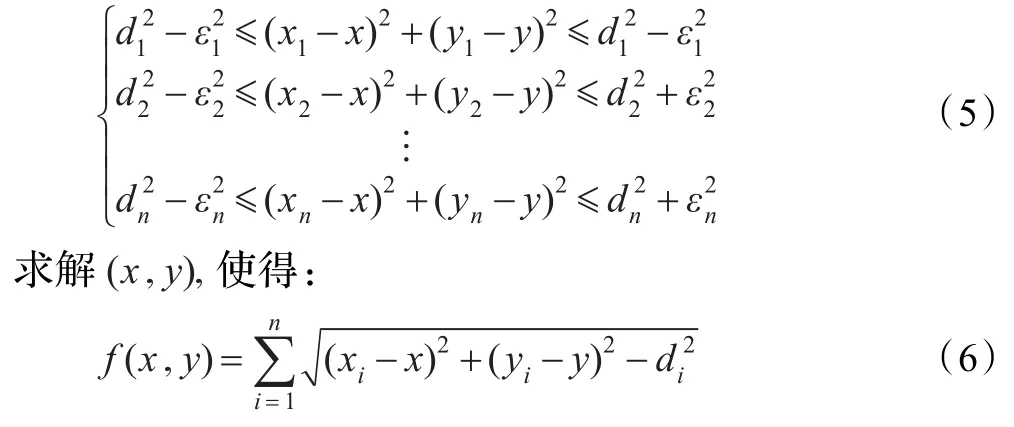
由于式（5）代表可行解的区域，那么该区域一定存在最优解，且当f(x，y)取最小值时，节点定位总误差最小，此时的坐标(x，y)将为最优值，这样无线网络传感器节点定位问题转化成一个约束优化问题，然后采用BA算法进行求解，提高传感器定位精度。

3 BADV-Hop算法的节点定位

3.1 改进的蝙蝠算法

2010年，有学者通过模拟蝙蝠回声定位行为而提出的蝙蝠算法（BA），其在迭代寻优方面相较其他群智能算法有很大优势。BA算法首先对所有蝙蝠的位置和速度随机初始化，其中位置是待求解问题的潜在解，然后通过适应度函数评价群体，找出群体最优个体（最优解）；接着分别按式（9）更新个体的脉冲频率、速度和位置：

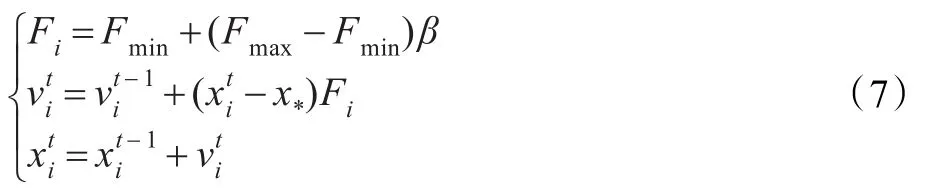
式中，Fi、Fmax和Fmin分别表示第i只蝙蝠在当前时刻发出的脉冲频率、脉冲频率的最大值和最小值，β∈[0，1]是一个服从均匀分布的随机因子，x*为最优蝙蝠位置。

据生物学知识，在初始阶段蝙蝠脉冲频度低且声响大，有助于在大范围内搜索目标，发现猎物后，逐渐使声响变小并增加脉冲频度以便精确掌握猎物的空间位置，因此声响和脉冲频度随着运行进行而不断地更新，公式如下：

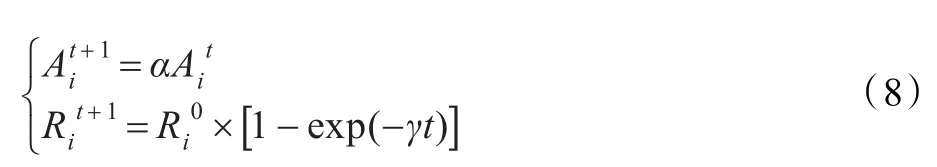
其中，0＜α＜1，γ＞0，均为常量。

随机飞动产生新解xi的公式为：

式中，ε∈[-1，1]是一个随机变量；At是所有蝙幅在此步中平均声音响度。

对BA算法原理进行分析可知，BA算法缺乏有效的变异机制，群体容易聚集于局部极值，导致早熟收敛，因此本文对其进行改进，并将其用于解决无线传感网节点定位问题，以提高定位精度。具体改进如下：

（1）蝙蝠通过调整频率Fi得到新的位置，在频率公式（4）中，β∈[0，1]区间内均匀分布的随机因子，其实质上是个体的变异操作，在一定的程度上使种群保持多样性，β是变异因子，其值越大，对新构建的解贡献越大；反之，值越小，对新构建的解贡献越小，控制好β值能提高种群多样性，避免早熟，从而提高算法的求精能力。因此本文采用动态自适应机制调整变异因子β，公式如下：

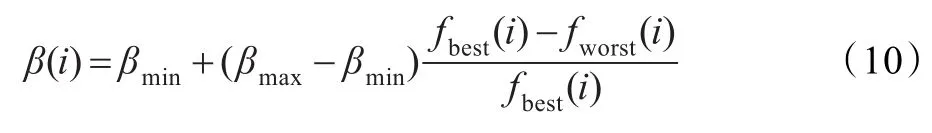
式中，fbest(i)是第i代最佳的适应度值；fworst(i)是第i代中最差的适应度值；(fbest(i)-fworst(i))/fbest(i)表示变异因子根据每代中最佳和最差适应度值完成自适应的调整。

（2）当rand＜Ri时，基本BA算法是通过随机飞动产生新解xi，相关研究表明，位置移动机制对算法优化精度、收敛速度有重要影响，基本BA算法中，蝙蝠移动后的位置目标函数值可能比原来的更差，因此，改进BA算法考虑以概率pa∈[0，1]抛弃最差的解，然后再用随机飞动重新生成相同数量的新解。

（3）当基本BA算法进行了n次迭代，最小值无变化或者变化很小，算法可能陷入局部最优，因此改进BA算法在n＞3且当前解的变化很小(＜1E-3)时，则考虑在当前解的基础上以莱维随机游动方式进行扰动，以扩大种群的搜索范围，评价并保留较好的解。莱维飞行是一种特殊的随机行走行为，体现出的是一类非高斯随机过程，其平稳增量服从Lévy稳定分布，则有蝙蝠位置更新公式为：

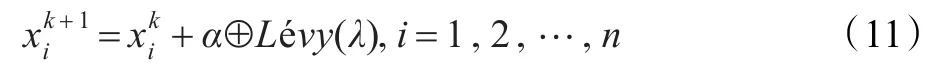
3.2 适应值函数设计

蝙蝠算法在优化的过程中，通过蝙蝠的适应度值来判断蝙蝠所处位置的优劣，蝙蝠算法种群中的每一个蝙蝠是未知节点的一个候选解，适应值函数计算公式为：

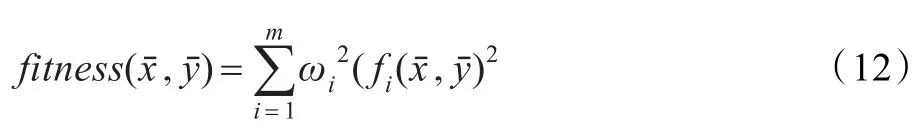
式中，m为锚节点的个数，ωi为未知节点与第i个锚节点测量距离的权重，其值与未知节点到锚节点的跳数hi成反比，hi由Dv-Hop算法的第一阶段获得，未知节点的估计距离是通过最小化适应度函数的目标值来决定的。

3.3 BADV-Hop算法的节点定位步骤

（1）在目标区域随机部署节点，先运用Dv-Hop算法的第一、二阶段定位方法，通过节点间相互通信，确保每个未知节点都接收并保存其到各锚节点的跳数hi和网络跳距di。

（2）在目标区域内随机初始化蝙蝠种群，种群中的每个蝙蝠都是当前未知节点位置的一个可行解，根据式（12）计算每个个体的适应值，保存群体最优位置x*以及群体最优值f(x*)。

（3）用式（7）调整搜索脉冲频率Fi，并计算蝙蝠个体的飞行速度vi，更新蝙蝠的空间位置xi。

（4）产生随机数rand，如果rand＞Ri，则接受新位置xi，否则，按发现概率pa丢弃差的个体，用式（11）产生新的位置替代丢弃的位置。

（5）如果(rand＞Ai)&&f(xi)＜f(x*)，则移动至更新后的位置，然后按式（10）更新脉冲频度Ri和声响Ai。

（6）判断是否出现连续3次f(x*)变化量小于1E-3的现象，若是，则转步骤（6），否则，转步骤（8）。

（7）根据式（10）对蝙蝠位置进行莱维随机扰动，评价并保留较好的解。

（8）判断是否满足结束条件（达到迭代次数或是预测精度），满足则结束；否则，转向步骤（3）。

（9）输出全局最优解对应的个体位置，即未知节点的位置估计坐标。

3.4 BADV-Hop算法的工作流程

借助于蝙蝠优化算法较强的寻优能力，首先在将DV-Hop算法未知节点坐标计算问题成果转换为全局最优化问题的基础上，然后采用利用改进蝙蝠算法代替最小二乘法来计算未知节点的坐标，以期较好地解决求解未知节点坐标时误差较大的问题，具体流程如图1。

4 仿真实例

4.1 仿真环境

为了验证BADV-Hop算法的有效性，在Matlab2012仿真平台上，在相同网络环境下选择标准DV-Hop算法进行对比实验，对不同锚节点密度、不同通信半径、不同节点数量以及定位精确度等方面进行了比较。在100 m× 100 m的二维区域中随机部署100个节点，节点的通信半径为30 m，锚节点的比例为10%，参数设置为：蝙蝠种群大小m=100，搜索脉冲频率范围[0，100]，最大脉冲频度r0=0.75，最大声响A=0.20，音量衰减系数，脉冲频度增加系数γ=0.05，所有结果为重复运行30次后取均值。采用平均定位误差评价定位算法的优劣，具体如下：

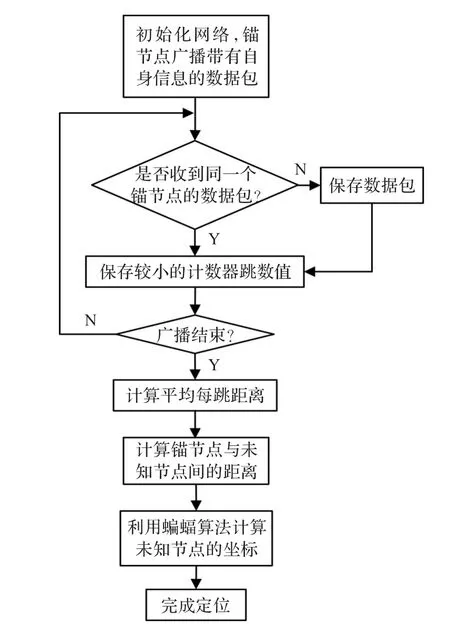
图1 BADV-Hop算法的工作流程

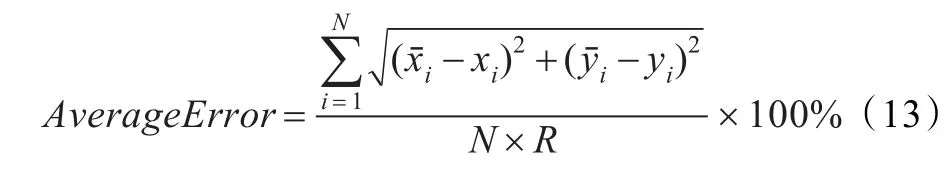
4.2 结果与分析

4.2.1 BA算法改进前后的收敛性能对比

改进前后BA的收敛曲线如图2所示。从图2可知，相对于基本BA算法，改进后的BA算法收敛速度明显加快，这主要是改进BA算法可以较好地保持种群多样性，以莱维随机游动方式进行扰动，扩大了种群搜索范围，提升了求解效率，可以较好地满足节点定位的实时性要求，并验证本文对BA算法改进的有效性和可行性。

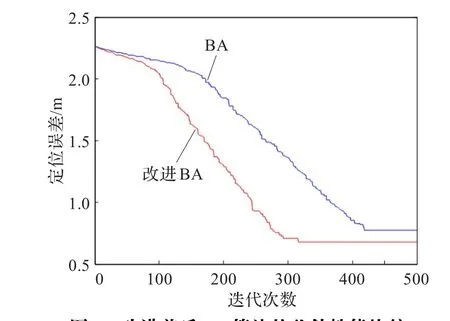
图2 改进前后BA算法的收敛性能比较

4.2.2 定位误差比较

DV-Hop算法、BADV-Hop算法的未知节点定位误差如图3所示。从图3可知，BADV-Hop算法得到的90个未知节点的平均定位误差相差不多，明显小于DV-Hop算法的结果，而且BADV-Hop算法的节点坐标偏离平均定位误差的幅度要明显小于DV-Hop算法的结果，对比结果表明，BADV-Hop算法具有更好的稳定性。

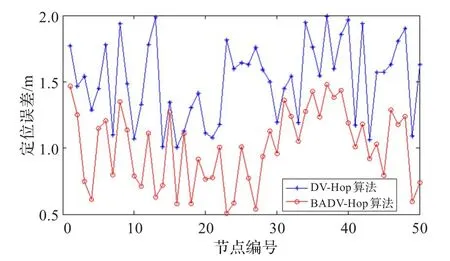
图3 两种算法定位的未知节点误差

4.2.3 不同锚节点个数下的定位性能

图4给出了2种算法定位性能随锚节点个数变化的曲线，其中节点总数为120，R=22 m。从图4可以看出，在相同锚节点比例下，相比于DV-Hop算法，BADVHop算法的平均定位误差总是小于DV-Hop算法的定位误差。

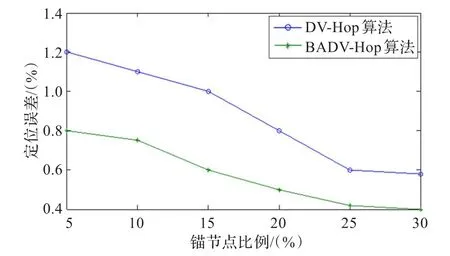
图4 不同锚节点个数下的定位性能

4.2.4 不同节点数下的定位性能

图5为节点个数从20变化为60时，两种定位算法的定位误差。由图5可知，相对于DV-Hop算法，BADVHop算法受到节点数量变化的影响相对较小，体现了很好的鲁棒性。

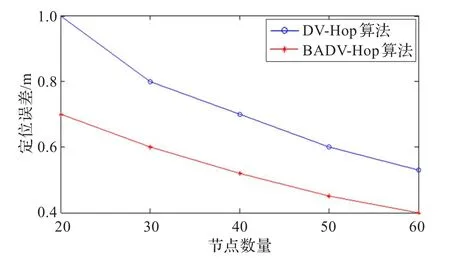
图5 节点密度对定位精度的影响

4.2.5 不同通信半径下的定位性能

图6为不同通信半径对两种算法定位性能的影响程度，其中锚节点比例为10%，节点个数为40。从图6可以看出，在相同节点通信半径下，相对于DV-Hop算法，BADV-Hop算法的定位精度提高了20%～40%，有效降低了传感器的定位误差。

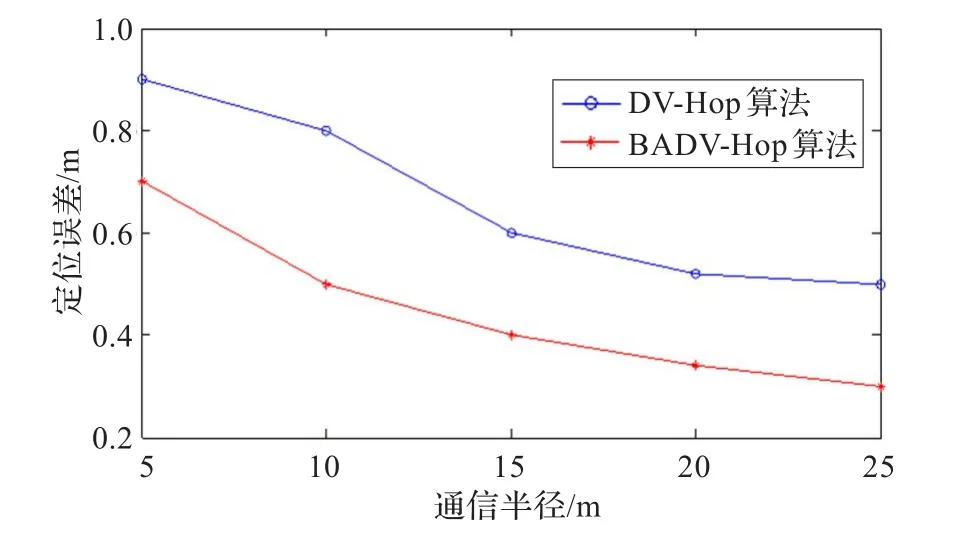
图6 不同通信半径下的定位性能

4.2.6 定位结果比较

DV-Hop算法和BADV-Hop算法的定位结果如图7所示。从图7可知，BADV-Hop算法的定位误差小于DV-Hop算法，且定位效果明显得以提高。

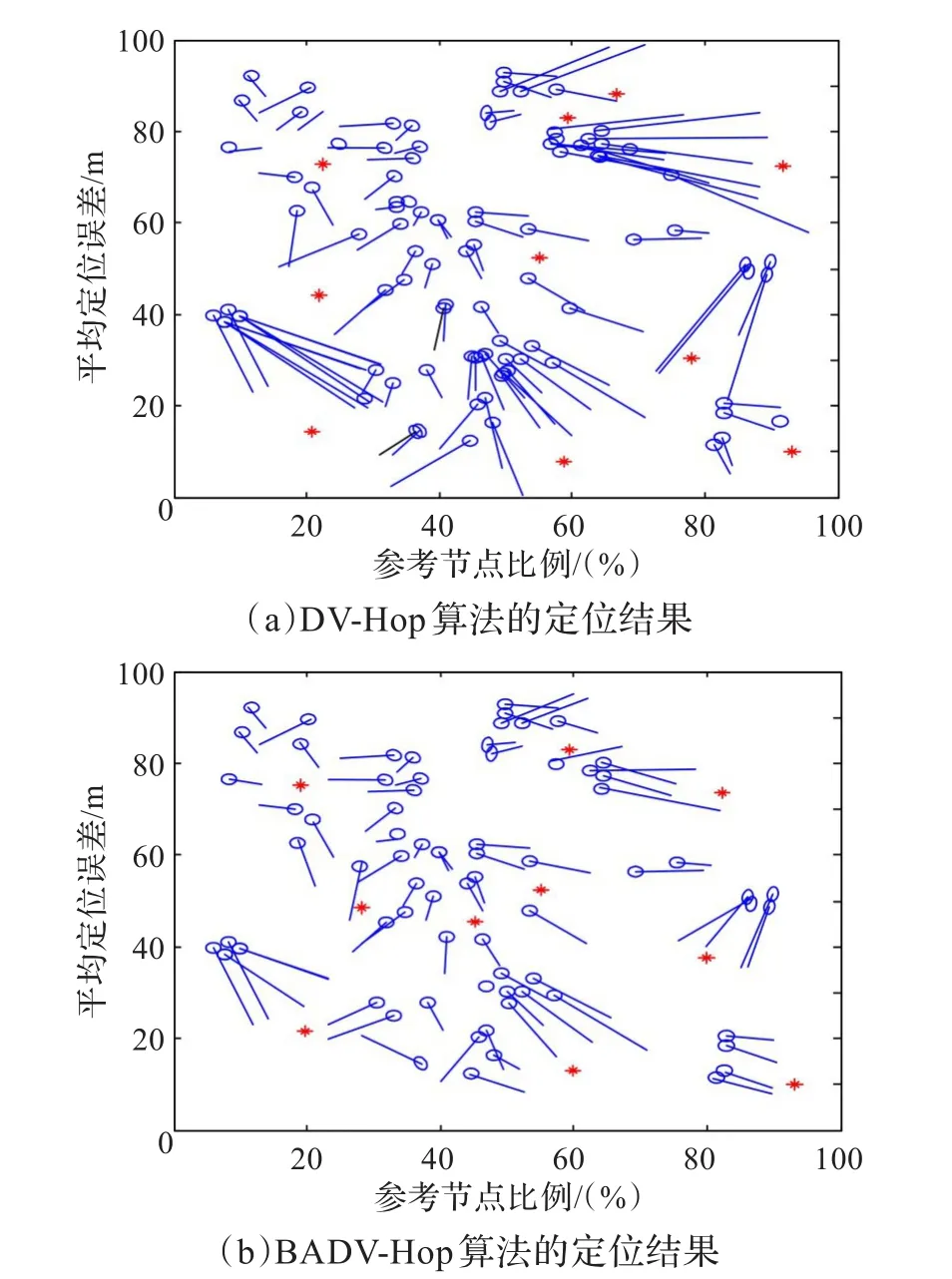
图7 两种算法的定位结果对比

5 结束语

为了提高无线传感器网络定位精度，提出一种蝙蝠算法和DV-Hop算法相融合的节点定位方法，在DV-Hop的第三阶段利用改进蝙蝠算法代替最小二乘法来计算未知节点的坐标，有效减少了平均跳距导致的定位误差，仿真结果表明，相比于DV-Hop算法，BADV-Hop算法在定位精度与平均定位误差方面具有明显优势。在此基础上，开展定位能耗、移动定位方面的改进将是下一步的研究重点。

[1]王福豹，史龙，任丰原.无线传感器网络中的自身定位系统和算法[J].软件学报，2005，16（5）：857-868.

[2]Costa J A，Patwari N，Hero O.Distributed weighted multidimensional scaling for node localization in sensor networks[J].ACM Transactions on Sensor Networks，2006，2（1）：39-64.

[3]刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权定位算法[J].传感技术学报，2009，23（5）：717-721.

[4]李辉，熊盛武，刘毅，等.无线传感器网络DV-Hop定位算法的改进[J].传感技术学报，2011，24（12）：1782-1786.

[5]白进京，严新平.基于加权质心和DV-hop混合算法WSN定位方法研究[J].计算机应用研究，2009，26（6）：2248-2251.

[6]Cerpa A，Estrin D.ASCENT：adaptive self-configuring sensor networks topologies[J].IEEE Transactions on M obile Computing，2004，3（3）：272-285.

[7]Gao Y，Zhao W S，Jing C，et al.WSN node localization algorithm based on adaptive particle swarm optimization[J]. Applied Mechanics and Materials，2012，143：302-306.

[8]叶蓉，赵灵锴.基于蚁群粒子群混合的无线传感器网络定位算法[J].计算机测量与控制，2011，19（3）：732-735.

[9]赵仕俊，孙美玲，唐懿芳.基于遗传模拟退火算法的无线传感器网络定位算法[J].计算机应用与软件，2009，26（10）：189-192.

[10]邓力.基于遗传算法WSN节点定位算法研究[J].计算机仿真，2011，28（9）：161-164.

[11]欧阳丹彤，何金胜，白洪涛.一种约束粒子群优化的无线传感网络节点定位算法[J].计算机科学，2011，38（7）：46-50.

[12]Yang X S，Gandom i A H.Bat algorithm：a novel approach for global engineering optimization[J].Engineering Computations，2012，29（5）：464-483.

TAN Aiping1，2,CHEN Hao1,WU Boqiao1

1.School of Information Science and Engineering,Hunan University,Changsha 410082,China
2.Hunan Industry Polytechnic,Changsha 410208,China

In order to reduce node localization error of wireless sensor network, a novel sensor node localization method is proposed based on Bat Algorithm and the DV-Hop algorithm（BA-DVHop）. In the third stage of DVHop algorithm, bat algorithm is used to take place the least square method to calculate the unknown node in order to reduce the positioning error, and bat algorithm is improved to avoid falling into local optimum, finally, the simulation analysis is used to test performance on Matlab 2012 platform. Compared with DV-Hop algorithm, BADV-Hop algorithm can improve the localization accuracy of wireless sensor network and has high application value, so the simulation results have verified the effectiveness of BA-DVHop algorithm.

wireless sensor network;bat algorithm;node localization;DV-Hop algorithm

TAN Aip ing,CHEN Hao,WU Boqiao.Nodes localization Method of wireless sensor networks based on Bat-DVHop algorithm.Computer Engineering and Applications,2014,50（17）：125-129.

A

TP393

10.3778/j.issn.1002-8331.1403-0094

国家自然科学基金（No.61272190）。

谭爱平（1979—），男，网络工程师，主研方向：网络工程、网络安全；陈浩（1977—），男，博士，副教授，主研方向：网络安全和信息安全；吴伯桥（1979—），男，网络规划师，主研方向：网络系统集成、网络安全。E-mail：476957437@qq.com

2014-03-10

2014-04-25

1002-8331（2014）17-0125-05