改进的RSA算法在数字签名中的应用

肖振久，胡驰，陈虹

1.辽宁工程技术大学软件学院，辽宁葫芦岛 125105

2.中国传媒大学计算机学院，北京 100024

改进的RSA算法在数字签名中的应用

肖振久1，2，胡驰1，陈虹1

1.辽宁工程技术大学软件学院，辽宁葫芦岛 125105

2.中国传媒大学计算机学院，北京 100024

针对传统RSA密码算法运算效率较低的问题，在标准RSA密码算法的自身结构和具体运算操作两方面做出了相应的改进，提出了一种新的RSA密码优化算法，并将该算法运用到数字签名技术中。然后通过仿真实验，将其与传统RSA算法以及基于乘同余对称特性的SMM算法和指数2k进制化相结合的组合优化算法相比较，实验结果表明新的RSA密码优化算法在提升运算速度方面达到了较高的水平。

RSA算法；数字签名；乘同余对称；模重复平方

1 引言

随着网络和通信技术的发展，在给人们带来益处的同时，也给人们带来了安全隐患。由于传输过程中存在数据被通信双方之外的第三方伪造或篡改的可能，通信双方无法验证数据来源，就很有可能出现一方抵赖的情况，此时就要求保证传输信息的不可否认性。数字签名就是通信双方在网上交换信息时，基于公钥密码体制来防止伪造和欺骗的一种身份认证技术，通信双方不需要实现交换密钥，保密性好。数字签名的算法很多，较为常见的有RSA签名[1]、DSA签名和椭圆曲线签名，其中RSA签名安全性高、易于实现，既可以用来加密数据又可以用于身份认证，因此得到了最为广泛的应用。但是它涉及到大数运算，其运算速度一直是RSA的瓶颈，目前虽然提出了许多的改进算法[2]，其中比较有代表性的就是将SMM算法和指数2k进制化算法相结合的组合优化算法，此算法相对于传统算法在运算速度上的确有一定提高，但效果仍不明显，本文提出一种在算法自身结构和运算操作上都加以改进的优化算法，实验证明，此算法相对于传统算法在运算效率上有较大幅度提高。

2 相关研究工作

2.1 数字签名技术原理

数字签名[3]过程如图1所示，分为签名和验证两个环节。假设用户A要发送消息X给用户B，首先A用自己的私钥d对X进行签名得Y=Sigd(X)，然后将X与Y一同发送给B，B接收以后需要用A的公钥e验证签名，计算X'=Vere(Y)，若X'=X，则说明消息确实来自于A，否则拒绝该签名。采用以上通信协议，若A否认曾发送消息X给B，用户B只需出示A的签名Y和公钥e给公证方，公证方采用正确的算法很容易证实签名确实属于A；若用户B伪造了消息X'，由于他不知道A的私钥，也就无法出示正确的签名，这样一来，通信双方都必须真实地反映通信情况，有效防止了一方抵赖的情形发生。

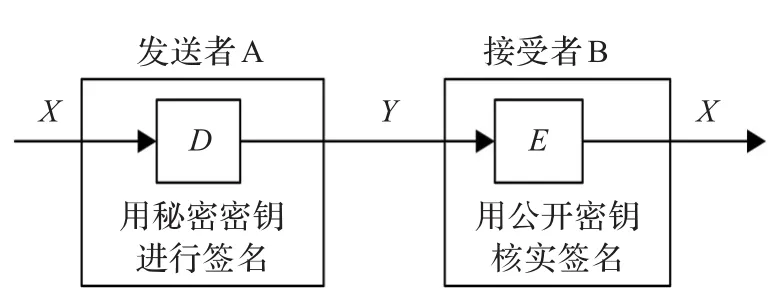
图1 数字签名过程

2.2 经典RSA数字签名方案

RSA数字签名方案[4]使用了RSA公开密钥密码算法进行数字签名，基本算法表述如下：

（1）选择大素数p、q，生成n、d、fn。其中，n=p×q、fn=(p-1)×(q-1)，选一整数e，满足1＜e＜fn，计算d，满足d×e≡1(mod fn)。公开模数n和公钥e，对于p、q、私钥d和fn严格保密。

（2）签名过程

假设用户A对数据M∈Zn进行签名，则计算：

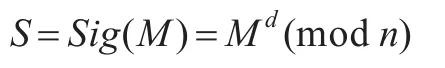
并将S作为用户A对数据M的数字签名附在数据M后。

（3）验证算法

假设用户B需要验证用户A对M的数字签名S，则用户B计算：

并判定M*是否等于M，若M*=M，则说明签名S确实是用户A所产生的，否则，签名S可能是伪造的。

2.3 SMM算法和指数2k次方化算法

由于RSA算法[5]在实际操作过程中存在运算效率低的瓶颈，许多的学者提出了不同的改进算法，这里重点介绍基于乘同余对称特性的SMM算法和指数2k次方化算法相结合的优化算法。

SMM算法[6]是利用乘同余对称特性来减少RSA算法中乘法和求模运算量的一种快速算法。传统的RSA算法是将指数x表示成t位二进制形式，并将幂剩余变成一系列的乘同余迭代，以a=gx(mod n)为例，每一步迭代必有运算a=a2(mod n)和可能有运算a=(a×g)(mod n)，此算法是在每步迭代计算中对乘数和被乘数进行进行有条件的代换：如果用ai-1表示第i-1步的迭代结果，则在进行第i步迭代时，若g≤(n-1)/2或ai-1≤(n-1)/2，则保持原数不变，否则用n-g或n-ai-1来代替g或 ai-1。

指数2k进制化算法[7]是通过缩短指数的长度来减少迭代次数的一种优化算法。该算法分两步进行：首先计算gXi(mod n)，其中Xi={0，1，2，…，2k-1}，需要计算从g0(mod n)到g2k-1mod n的每一个值，并将其存放在数组R中，然后进行幂剩余和同余计算：置变量c=1，对于i=m-1，…，1，0（m为指数2k进制化后的位数）重复执行c=c2k(mod n)和(c×R[xi])(mod n)，最后得到c即为所求。

把以上两种算法组合起来可得到一种新的组合优化算法，它的基本思路是：根据2k进制化算法将指数2k进制化，减短指数长度，通过迭代法把乘方后求模的计算改为在求乘方的过程中求模的计算，减少中间结果的数值，如果中间结果值大于模数的一半，则根据SMM算法用模数减去该值得到的差来代替中间结果值，并继续计算。通过实验，此优化算法在运算速度上有一定的提高，但效果仍不明显。

3 RSA算法的改进与优化

3.1 算法结构改进

RSA算法有着大量制约着执行效率的幂剩余运算，它的安全性又依赖着大整数n的因数分解，那么在不改变n的情况下把幂剩余运算减到最少就可以在保证安全性的情况下大幅度提高运算效率。于是，可以先把算法做一些改动：设明文分组m=(m1，m2，…，mk)，相应的密文分组为c=(c1，c2，…，ck)，按照RSA算法有：

（1）加密运算

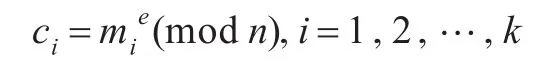
（2）解密运算

可见，加密和解密都要执行k次幂剩余运算。那么改进的思路是尽可能减少幂剩余运算的次数，最好的办法就是把幂剩余运算改为加法剩余运算[8]，算法如下：

（1）加密运算

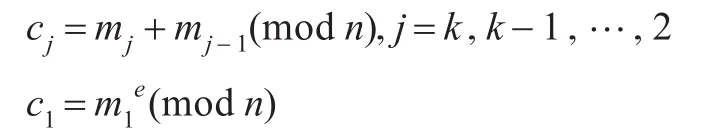
（2）解密运算

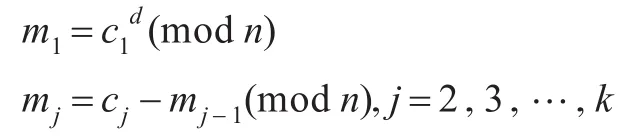
这样改动之后，加密和解密都只需进行1次幂剩余运算和k-1次加法剩余运算。而一次加法剩余运算比一次幂剩余运算至少快mimin(e，d)倍，因此，改进之后的算法比传统RSA算法运算速度至少快(k-1)mimin(e，d)倍。改进后的算法安全性取决于第一个明文分组m1的抗破译性，只要第一个明文分组不被破译，攻击者便无法恢复出明文m。而第一个明文分组的安全性与传统RSA算法一样，都依赖于分解模数n的困难性，数学上，至今还没有人提出有效的大数分解方法。因此，改进后的算法抗破译能力并没有降低。

3.2 运算操作改进

由于在实际操作中，为了保证安全，p和q都是1 024位二进制数，那么n就是2 048位的二进制数，换算成十进制600多位，它的幂剩余运算仍然值得去做优化，这里，采用的是一种模重复平方算法的rho改进算法。

首先介绍一下模重复平方算法[9]，若要计算bn(mod m)，先将指数n写成二进制：n=n0+n1×2+…+ nk-1×2k-1，则bn≡bn0(b2)n1…(b2k-2)nk-2(b2k-1)nk-1(mod m)，再按下列步骤计算：

（1）令a=1，b0=b。

（2）如果n0=1，则计算a0≡a×b0(mod m)否则取a0=a，再计算b1≡b02(mod m)。

（3）如果n1=1，则计算a1≡a0×b1(mod m)否则取a1=a0，再计算b2≡b12(mod m)。

……

（4）如果nk-2=1，则计算ak-2≡ak-3×bk-2(mod m)，否则取ak-2=ak-3，再计算bk-1≡bk-22(mod m)。

（5）如果nk-1=1，则计算ak-1≡ak-2×bk-1(mod m)，否则取ak-1=ak-2，最后，ak-1就是所得结果。

在以上算法中，由于b0=b，bi+1≡bi+2(mod m)(i=0，1，…)，但Zm是有限的，所以序列bi有一个周期。即存在j，w，使得bj=bj+w，那么，序列b0，b1，…，bj-1可以画成一个rho(ρ)的“尾”，而回路bj，bj+1，…，bj+w-1，可以看成rho的“体”。bk叫做bk+1的前导，bk+1叫做bk的后继。把满足bj=bj+w最小的j叫做序列bi的索引，记为λ，把满足bj=bj+w的最小w叫做序列bi的周期，记为μ，rho结构如图2[10]所示。

图2 rho结构图

使用Floyd循环查找算法，从数对(b1，b2)开始，由前一数对(bi-1，b2i-2)来迭代计算(bi，b2i)直到某个w处，bw=b2w。用“/”表示除以，所得结果向下取整，第一次bw=b2w时，w=μ(1+λ/μ)。注意，这里λ＜w≤λ+μ。令θ=w，如果bw=bw+θ/2，则θ除以2，循环这一过程，最终的θ就是所求周期μ。令α=-1，β=w，如果bα+(β-α)/2= bα+(β-α)/2+μ，令β=α+(β-α)/2，否则，令α=α+(β-α)/2，循环这一过程，直到β-α=1，β就是所求的索引λ。

下面研究rho“体”上元素的性质。

性质1令M=bjbj+1bj+2…bj+w-1，则对任意整数n＞0，X有：XM≡XMn(mod m)。

在引出下面一条性质之前，先说明“循环二进位”的概念。向量(t0，t1，…，tn)（其中ti∈N）的循环二进位是把t0，t1，…，tn看成二进制的低位到高位，从低位到高位满2进1，到最高位时满2再向最低位进1，循环这一过程直到t0，t1，…，tn只有0或1。例如向量（3，4，4，6）的循环二进位过程为：（3，4，4，6）→（1，4+1，4，6）→（1，1，6+ 2，4）→（1，1，0，4+4）→（1+4，1，0，0）→（1，1+2，0，0）→（1，1，1，0），则向量（1，1，1，0）即为向量（3，4，4，6）的循环二进位结果。

利用这两条性质，可得模重复平方算法的rho改进算法：

（1）令a=1，b0=b，并将n写成二进制。

（2）计算并存储bi，同时使用Floyd循环查找算法查找w。如果找到w则停止计算bi，并根据前面的算法计算出周期μ和索引λ；如果w不存在则令μ=0。

（3）如果μ为0，按照模重复平方算法的计算步骤从a0计算到ak-1，则bn≡ak-1(mod m)。

（4）如果μ为1，则M=bλ。由性质1，如果bλ=0，则bn≡0(mod m)，否则，令nλ=1，按照模重复平方算法的计算步骤从a0计算到aλ，则bn≡aλ(mod m)。

（5）如果λ＞1，nλ，nλ+1，…，nλ+μ-1及其后面的ni每隔μ为一个单位（不足μ位后面补0）平移叠加到一组初始值为0的零时变量tλ，tλ+1，…，tλ+μ-1。由性质2，对叠加后的tλ，tλ+1，…，tλ+μ-1进行循环二进位，并把tλ，tλ+1，…，tλ+μ-1的值分别赋值给nλ，nλ+1，…，nλ+μ-1。按照模重复平方算法的计算步骤从a0计算到aλ+μ-1，则bn≡aλ+μ-1(mod m)。

这种算法的实质是一种指数约减算法，可以有效减少模重复平方算法中的模乘运算。由此可见，新的改进算法，先从结构上把幂剩余运算的次数减到最低，再从算法操作上把一次幂剩余运算中的模乘减到最低，这样大幅度地减少了计算机中最耗时的运算，它的运算速度将会有极大地提高。下面将通过实验来对比三种算法在数字签名中的耗时情况。

4 实验结果及比较分析

本次实验的硬件环境为：Pentium®4 CPU 3.06 GHz、512 MB内存、80 GB硬盘；操作系统为：window s XP；开发工具：Visual C++6.0。本程序旨在比较相同环境下3种算法的性能，所以选取小素数进行多次测试。为了防止溢出，取p=157、q=223、n=35 011、fn=34 632，e取4 097，算得d=25 097。由于C++标准中时间只能精确到毫秒，如果数据量太小将无法产生实验结果，因此采用一个随机生成特定长度字符串的函数分别对1 MB、10 MB、30 MB、50 MB的数据量用经典RSA数字签名方案进行签名，考虑到机器对算法效率的影响，对每种长度的数据量做5次签名再取平均时间，实验结果如表1所示。

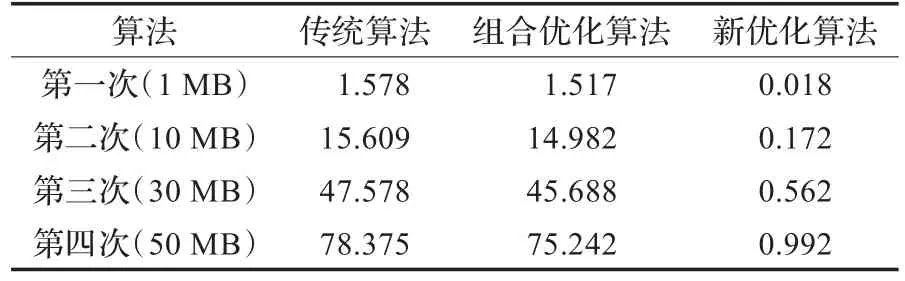
表1 算法平均耗时s

从以上的实验数据可以看出，组合优化算法相对于传统算法平均可以提速4%，而新优化算法相对于传统算法和组合优化算法均可提速98%，这无疑是一个质的飞跃，特别是当数据量越大，分组越多时，签名速度提高得越明显。

5 结束语

由于传统的RSA加密算法存在大量的模幂运算，这一直是制约其运算速度的瓶颈。本文提出一种新的优化算法，先从结构上把模幂运算的次数降到最低，再从运算上把一次模幂运算中的模乘运算次数降低，最后通过理论分析和仿真实验，得出新的优化算法在保证安全性的前提下，其运算速度较传统RSA算法有较大幅度提高这一结论。新算法的不足之处是其中的模重复平方算法的rho改进算法实现起来比较复杂，如何进一步简化该算法，这是下一阶段重点研究的方向。

[1]Fu C.An efficient implementation of RSA digital signature algorithm[C]//4th International Conference on Wireless Communications，Networking and Mobile Computing，2008：1-4.

[2]Liu Qing.Two efficient variants of the RSA cryptosystem[C]//2010 International Conference on Computer Design and Applications（ICCDA），2010：550-553.

[3]杨波.现代密码学[M].北京：清华大学出版社，2007.

[4]胡方.改进的RSA算法及其在数字签名中的应用[D].沈阳：东北大学，2008.

[5]Stalling W.密码编码学与网络安全—原理与实践[M].5版.北京：电子工业出版社，2011.

[6]周升力.RSA密码算法的研究与快速实现[D].南昌：南昌大学，2008.

[7]贺令亚.RSA加密算法的研究与实现[D].长沙：中南大学，2009.

[8]苏开元.DES_RSA混合加密以及传输实现[D].南京：南京邮电大学，2012.

[9]陈恭亮.信息安全数学基础[M].北京：清华大学出版社，2004.

[10]石小平，姜浩.模重复平方算法的rho改进算法[J].计算机应用与软件，2011，28（12）：48-50.

XIAO Zhenjiu1，2,HU Chi1,CHEN Hong1

1.College of Software, Liaoning Technical University, Huludao, Liaoning 125105, China
2.School of Computer, Communication University of China, Beijing 100024, China

In order to enhance the operation efficiency of RSA algorithm, a new improved algorithm is suggested in this paper which makes some improvements in structure and operation, and it is applied to digital signature. The experiment makes comparison between a combinatorial optimization algorithm which combines SMM with index of 2k hexadecimal algorithm and the new algorithm. It shows that the new algorithm reaches a high level in operation speed.

RSA algorithm;digital signature; Symmetry of Modulo Multiplication（SMM）; modular repeated squaring algorithm

XIAO Zhenjiu, HU Chi, CHEN Hong. Improved RSA algorithm and application in digital signature. Computer Engineering and Applications, 2014, 50（17）：106-109.

A

TP309.7

10.3778/j.issn.1002-8331.1210-0044

国家自然科学基金（No.61103199）；北京市自然科学基金（No.4112052）。

肖振久（1968—），男，副教授，研究领域为网络与信息安全、数字版权管理；胡驰（1988—），男，硕士研究生，研究领域为数据加密、数字签名；陈虹（1967—），女，副教授，研究领域为网络安全。E-mail：hcshrhh001@163.com

2012-10-08

2012-12-27

1002-8331（2014）17-0106-04

CNKI网络优先出版：2013-01-18,http://www.cnki.net/kcms/detail/11.2127.TP.20130118.1024.006.htm l