互联网中的模糊滑模拥塞控制策略

闫明，冯春杨，高飞雪

辽宁大学轻型产业学院，沈阳 110036

互联网中的模糊滑模拥塞控制策略

闫明，冯春杨，高飞雪

辽宁大学轻型产业学院，沈阳 110036

针对互联网中的拥塞控制问题,基于滑模控制理论及T-S（Takagi-Sugeno）模糊模型，提出了一种模糊滑模拥塞控制策略。考虑到互联网中存在的不确定和时变时滞因素，采用T-S模糊模型对网络系统进行了建模。利用线性矩阵不等式设计了一个渐近稳定的滑模面，有效地补偿了不确定及时滞因素的影响。基于趋近律的方法设计了控制器，有效地抑制了路由器中队列长度的振荡。多种情况下的仿真对比表明，所提出的控制策略具有更好的稳定性和鲁棒性。

互联网拥塞控制；滑模控制；T-S模糊模型；主动队列管理

1 引言

互联网在过去近二十年中得到了爆炸式的增长及流行，极大地方便了人们的生产和生活，然而随着互联网用户数量的急剧膨胀，拥塞问题却越来越严重地阻碍了网络的健康发展，使得网络的性能大大下降，用户的上网速度受到了很大的影响。因此，设计一种有效的拥塞控制算法已成为网络管理中急待解决的关键问题。

主动队列管理（Active Queue Management，AQM）是高速路由器的一个重要模块，同时也是基于路由器的一种拥塞控制机制，该机制通过在路由器队列满之前就以一定的概率标记或丢包，使发送端能够及早作出反应，如减小发送速率等，从而达到抑制拥塞的目的，AQM与TCP（transmission Control Protocol，传输控制协议）端到端的拥塞控制相结合，是目前解决互联网拥塞控制问题的一个主要途径[1]。

近年来，主动队列管理已成为一个很活跃的研究领域，相继产生了一些AQM算法[2-3]，取得了一定的拥塞控制效果。然而互联网是一个异常复杂的时变系统，避免其中的不确定性因素的影响几乎是不可能的。为此，需要设计一种鲁棒性更强的主动队列管理控制器才能取得更好的控制效果。滑模控制算法与其他控制算法相比，最大的优势就是在一定的条件下具有不变性，或称为理想鲁棒性[4]。对于异常复杂的互联网而言，采用滑模算法进行拥塞控制是相当理想的选择。近年来，相继出现了一些该方面的拥塞控制算法[4-6]。文献[4]考虑到不确定和输入时滞的影响设计了性能更好的趋近律，有效地降低了路由器中队列长度的振荡。文献[5]基于滑模控制思想设计了一种主动队列管理控制器SMVS，极大地提高了系统的鲁棒性，文献[6]考虑到了网络中的时变时滞因素，在可用带宽范围内降低了数据包的丢失率。但以上文献均只适合线性系统模型，当网络中的各种不确定和时变时滞因素使系统偏离平衡点时，线性系统模型所带来的误差就会加大，而直接对非线性的网络模型进行分析设计又十分困难。

T-S（Takagi-Sugeno）模糊模型已被证明能够以很高的精度近似代替一个非线性系统[7]，因此，若将滑模控制和T-S模糊控制相结合设计一种新的拥塞控制器，发挥二者各自的优势，则势必能进一步提高控制器的拥塞控制效果。近年来，这方面的研究也取得了一些成果[8-9]。这些文献虽然在一些方面收到了较好的效果，但也存在着各自的局限性，如有的文献没有考虑到时变时滞因素对网络的影响，有的文献中的控制器存在一定的抖振现象，稳态特性不够理想等等。总之，该领域仍有较大的研究空间。

本文为更好地解决互联网中的拥塞控制问题，基于T-S模糊模型为互联网的主动队列管理提出了一种滑模控制算法。利用T-S模糊模型来近似代替原有的非线性网络拥塞控制系统，提高了算法所基于的模型的精度。同时也考虑到了网络中存在的各种不确定和时变时滞因素的影响，利用LM I（Linear M atrix Inequality，线性矩阵不等式）设计了一个渐近稳定的滑模面，将滑模面的设计问题转化为LM I的求解问题。基于趋近律的方法设计的控制器能够有效克服路由器中队列长度的稳态振荡。多种情况下的仿真对比证实了本文算法的优越性。

2 互联网拥塞控制模型

据统计，互联网上95%的数据流，如HTTP、FTP、TELNET等均使用TCP作为其传输层协议[10]，因此，使用TCP网络拥塞控制模型来分析互联网有其合理性。文献[2]应用流体流理论给出了非线性TCP网络拥塞控制模型，如下所示：

其中，W(t)为TCP网络的窗口大小，q(t)为路由器中当前的队列长度，R(t)为往返时延，0≤p(t)≤1为分组丢弃/标记概率，N(t)为激活的连接数，C(t)为主干链路容量。

令x1(t)=q(t)-q0，x2(t)=W(t)-W0，τ(t)=R(t)，u(t)= p(t)-p0，q0为路由器中期望的队列长度，W0为TCP网络窗口的期望值，p0为p(t)的期望值，假设τ˙(t)≤d＜1（即往返时延的变化率较慢），则式（1），（2）可化为：

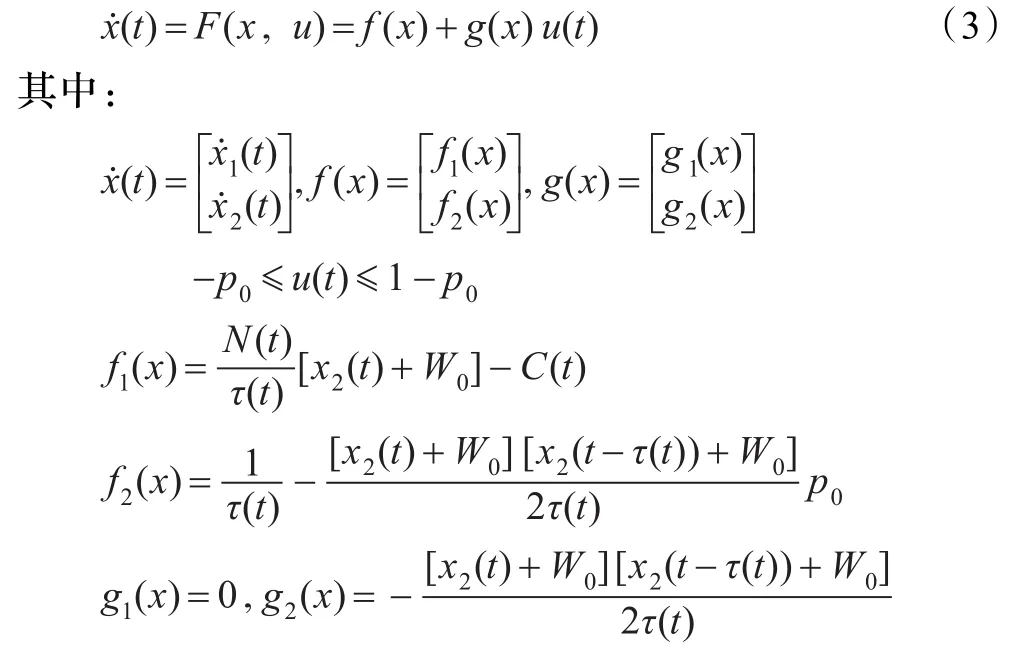
由于式（3）为非线性系统，因此直接对其进行分析和设计十分困难，而采用T-S模糊模型对式（3）进行近似代替的方法能够使问题得以解决。T-S模糊模型用一组“如果-那么”模糊规则来描述式（3）的行为，从式（3）中可以看出，每条模糊规则所对应的模糊状态方程中应包含x(t)和x(t-τ(t))项，这样比较合理，因此第i条模糊规则所对应的模糊状态方程取为：

规则i：如果x1(t)为并且x2(t)为F，那么

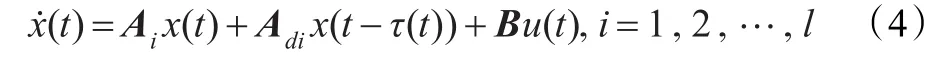
其中，x1(t)，x2(t)为状态变量，对于T-S模糊模型而言即为前件变量，u(t)为控制量且满足-p0≤u(t)≤1-p0，，为模糊子集，l为模糊规则数，Ai，Adi，B为适当维数的常数矩阵。

由于在实际的互联网中，活动的TCP连接数、链路带宽及往返时延常常都是变化的。同时，互联网中也存在着一定数量的非TCP数据流，如UDP数据流等，所有这些不确定和时滞因素都将影响到模型的精度，相当于干扰项。因此用如下的带有干扰项的系统来描述第i条模糊规则所对应的模糊状态方程更加合理，即

规则i：如果x1(t)为并且x2(t)为，那么

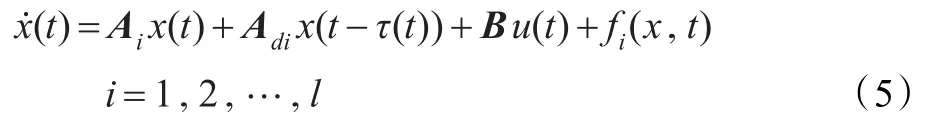
其中，fi(x，t)代表互联网中的干扰项。

注意到在实际的互联网中，尽管存在着各种各样的不确定和时滞因素，但它们的变化都是有一定范围的，即TCP连接数的变化不会超过路由器的固有容量，链路带宽的变化不会超过带宽的上限，往返时延的变化受传输距离的限制也有一定的范围，因此代表这些不确定性因素的fi(x，t)也应是范数有界的，不妨设fi(x，t)满足如下不等式：

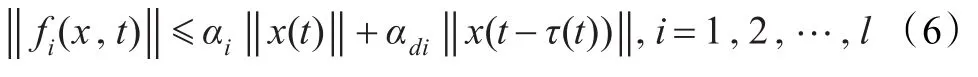
其中，αi＞0，αdi＞0为适当选取的常数。

引理1[11]不确定非线性函数f(x，t)范数有界，即存在常数α1＞0，αd1＞0，使得f(x，t)满足如下不等式：

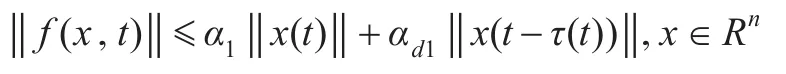
那么f(x，t)满足如下等式：

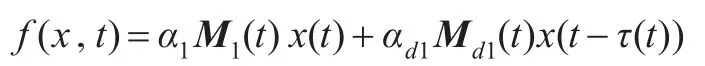
其中，M1(t)和Md1(t)为不确定项且满足M1T(t)M1(t)≤I，Md1T(t)Md1(t)≤I，I为单位矩阵。

根据引理1，式（5）能够被重写为如下形式：规则i：如果x1(t)为并且x2(t)为，那么

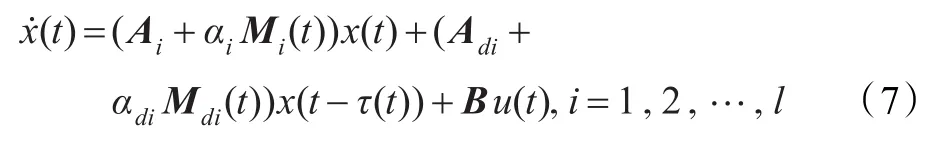
对式（7）采用单点模糊化、乘积推理和加权平均反模糊化得到系统的全局模糊状态方程如下：

在上述T-S模型的建模中，Ai，Adi，B的取值是依据文献[7]中的方法并结合式（3）而得到的，即它们是在式（3）的具有代表性的特征点(x0，u0)附近进行局部线性化处理而得到的，如果特征点(x0，u0)是系统的平衡点，则

式（8）即为本文算法所基于的互联网拥塞控制系统的数学模型，本文的目标是使该系统稳定，即通过所设计的控制器的作用使x(t)趋近于零，亦即路由器中的队列长度q(t)能够最终收敛于期望值q0，从而防止拥塞现象的发生，并使这一控制过程具有良好的稳定性和鲁棒性。

3 滑模拥塞控制算法的设计

3.1 滑模面的设计

定义滑模面为：

其中，P为待求的对称正定矩阵。目标是通过选择一个适当的P，使这个滑模面上的滑模运动方程具有渐近稳定性。

为了获得该滑模面上的滑模运动方程，对x(t)进行如下的变换：

当系统状态运动到滑模面上时，S(t)=0，由式（13）知，此时z2(t)=0，即滑模面上的系统状态不包含z2(t)。由式（12）易知x(t)=P˜z1(t)，并注意到B=0，因此，滑模面上的滑模运动方程为：

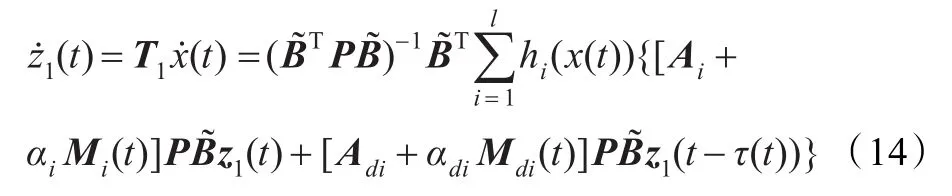
引理2[12]给定适当维数的矩阵D，E和M(t)，如果M(t)满足MT(t)M(t)≤I，则对任意一个常数λ＞0，有不等式DM(t)E+ETMT(t)DT≤λ DDT+λ-1ETE成立。

利用引理2，可以得到如下定理：

定理1如果存在对称正定矩阵P和Q，及常数λ1＞0，λ2＞0，使得如下的LM I成立：

本文立足于新时代背景下的共享经济，对价值共创相关研究文献进行阐述，定义共享型生活服务平台及其特性，对基于共享型生活服务平台的社区各要素间的价值共创过程进行具体分析，识别其价值清单，对价值共创和顾客忠诚度研究都是有益的补充。

对式（19）利用矩阵的Schur补性质知，式（19）成立等价于定理1中的式（15）成立，即当式（15）成立时，V˙(t)＜0，从而使所设计的滑模面（11）上的滑模运动方程（14）渐近稳定，定理证毕。

注1可用Matlab软件中的LM I工具箱求出式（15）中的矩阵P，从而完成滑模面S(t)的设计。

3.2 滑模拥塞控制器的设计

该部分将设计一个滑模拥塞控制器，使其满足如下形式的趋近律：

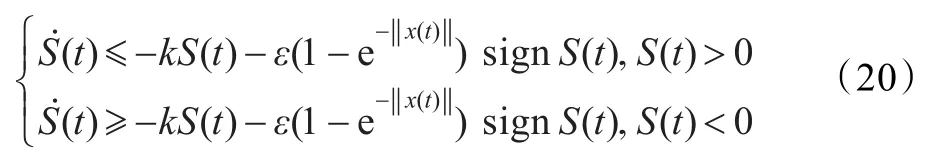
其中，k，ε均为大于零的常数，注意到当x(t)≠0时，0＜(1-e-‖x(t)‖)＜1。

由文献[4]知，满足该趋近律的控制器能够使路由器中的队列长度快速收敛于期望值并且稳态时的振荡很小。

定理2如果为式（8）设计的滑模拥塞控制器具有如下的形式，则该控制器能够满足趋近律式（20）：

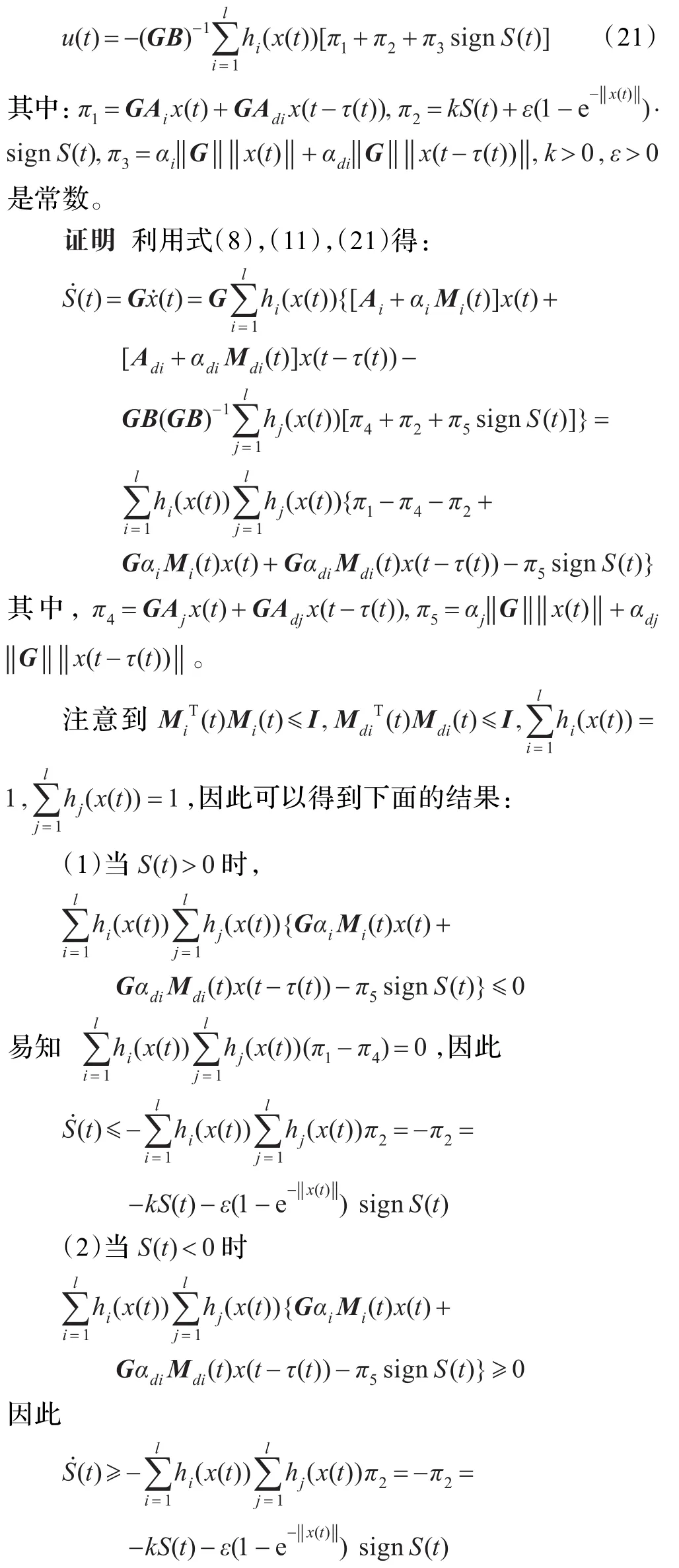
因此，所设计的滑模拥塞控制器（21）能够满足趋近律（20），定理证毕。

4 仿真结果

采用NS2仿真平台的网络拓扑结构如图1所示，即有N个发送端和N个接收端，路由器1为拥塞发生的位置，本文算法（FSMC，模糊滑模控制）即工作在其中，即为路由器中的一个用于拥塞控制的功能模块，具体实现时应通过计算机编程的方法将本文算法固化在路由器相应的芯片中。

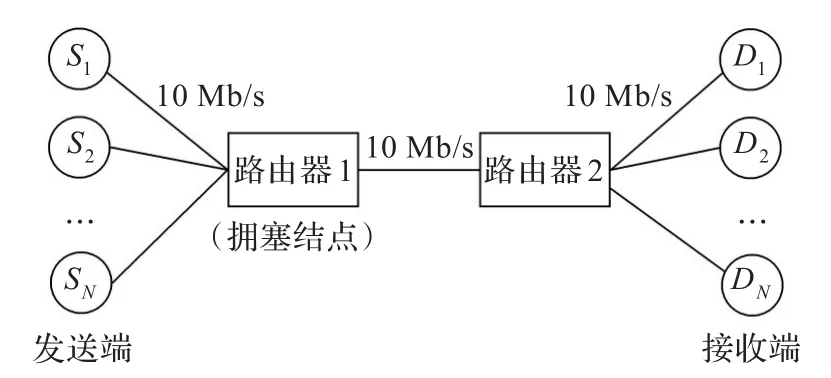
图1 仿真网络拓扑结构

在T-S模糊模型的建模时，选择式（3）的两个具有代表性的特征点：一个为系统的平衡点，记为(x01，u01)，显然x01=[0 0]T；另一个为q(t)在期望值附近且TCP网络的窗口大小在最大值附近的那点，记为(x02，u02)，根据前述参数易求得x02=[0 104]T。在这两个特征点附近对式（3）进行局部线性化处理，得到如下的两条模糊规则：

规则1：如果x1(t)在0附近并且x2(t)在0附近，那么x˙(t)=(A1+α1M1(t))x(t)+(Ad1+αd1Md1(t))x(t-τ(t))+B u(t)

规则2：如果x1(t)在0附近并且x2(t)在104附近，那么x˙(t)=(A2+α2M2(t))x(t)+(Ad2+αd2Md2(t))x(t-τ(t))+B u(t)

根据上述网络参数及式（9），（10）得：

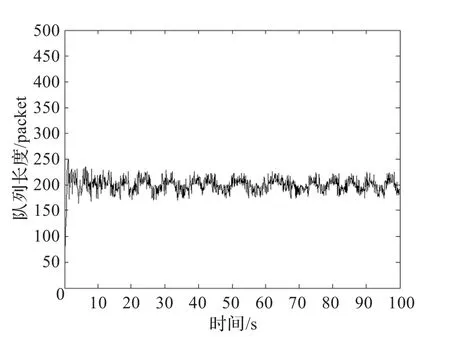
图2 使用SMVS时的队列长度

兼顾简单有效的原则，选取如下形式的指数函数作为隶属函数：

为了比较，在相同的网络条件下，也对文献[5]中的滑模拥塞控制器（SMVS）做了仿真，结果如下：

（1）网络的静态性能

在这一试验中，网络的参数选择同上所述，并且假设网络参数是不变的，仿真结果如图2和图3所示。

从图2和图3中可以看出：SMVS算法虽然使路由器中的队列长度趋于稳定，但由于没有采用有效的抑制抖振的措施，导致系统在稳态时存在一定幅度的振荡，稳态特性不够理想；本文算法（FSMC）能够有效地抑制抖振现象，因此经过较短的调整时间后系统趋于稳定，稳态时队列长度基本上达到了期望值。

（2）网络的鲁棒性能

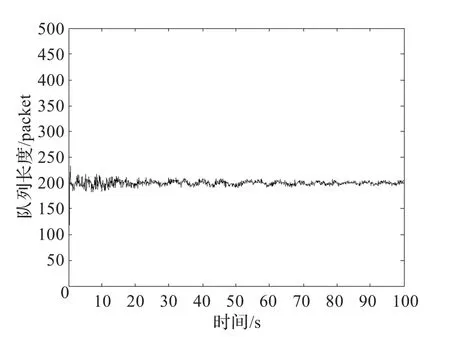
图3 使用FSMC时的队列长度

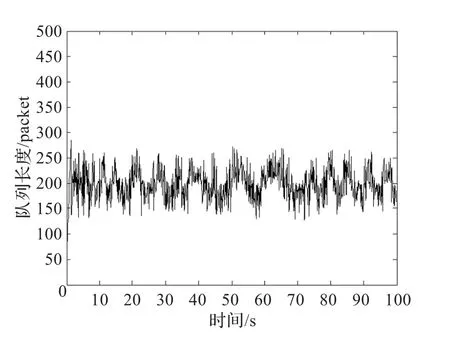
图4 使用SMVS时的队列长度

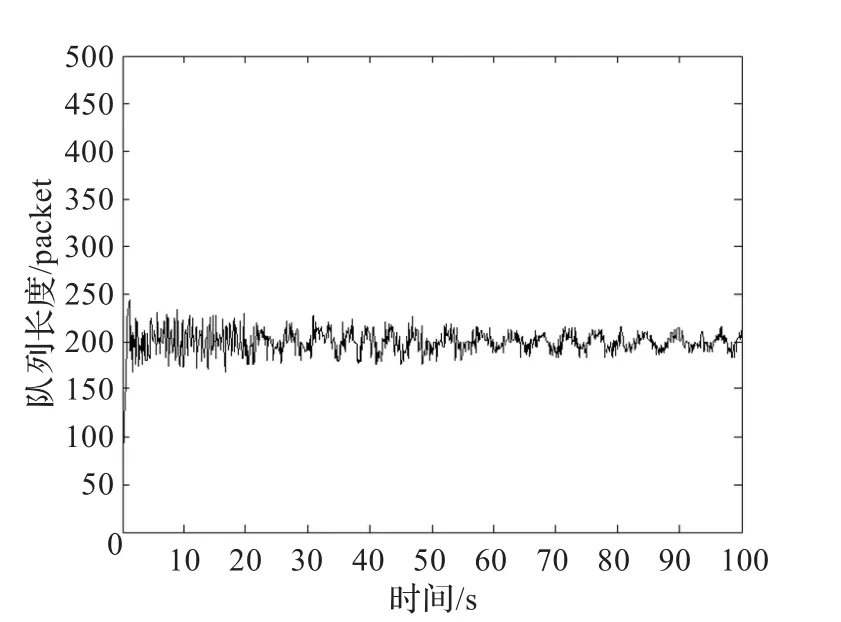
图5 使用FSMC时的队列长度

这里使TCP连接数N(t)在70至130之间随机变化，链路带宽C(t)在0.8×104packet/s到1.2×104packet/s之间随机变化，往返时延R(t)在80 ms到120 ms之间随机变化，仿真结果如图4和图5所示。

从图4和图5中可以看出：SMVS和FSMC控制器对变化的网络参数均不敏感，但SMVS达到稳态所需的时间更长，振荡也较大；而FSMC则具有更短的调节时间和更好的稳态性能，这是由于FSMC算法所基于的数学模型更为精确，并且算法考虑到了不确定和时变时滞因素的影响，从而使得队列长度在经过短暂的调整后迅速接近于期望值。

5 结论

针对互联网中的拥塞控制问题，本文基于T-S模糊模型提出了一种滑模主动队列管理算法。该算法将原有的非线性网络模型用T-S模糊模型来近似代替，同时考虑到了互联网中存在的各种不确定和时变时滞因素的影响，利用线性矩阵不等式设计了滑模面，该滑模面能够保证其上的滑模运动渐近稳定。基于趋近律的方法设计的控制器能够有效地抑制路由器中队列长度的振荡，并使其快速收敛到期望值，从而更好地改善了路由器的拥塞控制性能。不同情况下的仿真对比证实了本文算法具有更好的稳定性和鲁棒性。

[1]Hollot C，Misra V，Towsley D，et al.Analysis and design of controllers for AQM routers supporting TCP flows[J].IEEE Transactions on Automatic Control，2002，47（6）：945-959.

[2]Misra V，Gong W B，Towsley D.Fluid-based analysis of a network of AQM routers supporting TCP flows with an application to RED[C]//Proceedings of ACM/ SIGCOMM，Sweden，2000：151-160.

[3]Mohamed F Z，Halima E，Farouk K.A prediction-based active queue management for TCP networks[C]//IEEE Symposium on Computers and Communications，2012：271-276.

[4]Yan M，Jing Y W，An Y L.Congestion control over Internet with uncertainties and input delay based on variable structure control algorithm[C]//IEEE International Conference on Mechatronics and Automation，New York，2007：1788-1793.

[5]Ren F Y，Lin C，Yin X H.Design a congestion controller based on sliding mode variable structure control[J].Computer Communications，2005，28（8）：1050-1061.

[6]Przemyslaw I，Andrzej B.Discrete-time sliding-mode congestion control in multisource communication networks with time-varying delay[J].IEEE Transactions on Control Systems Technology，2011，19（4）：852-867.

[7]吴忠强，许世范，岳东.非线性系统的T-S模糊建模与控制[J].系统仿真学报，2002，14（2）：253-256.

[8]尹凤杰，岳承君.基于模糊调节滑模面的TCP拥塞控制算法研究[J].计算机工程与应用，2008，44（15）：85-87.

[9]张伟，孙秀霞，秦硕，等.自适应模糊全局快速Term inal滑模控制方法[J].计算机工程与应用，2009，45（27）：228-230.

[10]Caserri C，Meo M.A new approach to model the stationary behavior of TCP connections[C]//Proceedings of IEEE INFOCOM，Telaviv，Israel，2000：367-375.

[11]Wang L Y，Zhan W.Robust disturbance attenuation with stability for linear systems with norm-bounded nonlinear uncertainties[J].IEEE Transactions on Automatic Control，1996，41（6）：886-888.

[12]Xie L H，Lu L L，Zhang D.Improved robust H2 and H∞ filtering for uncertain discrete-time systems[J].Automatica，2004，40（5）：873-880.

YAN Ming, FENG Chunyang, GAO Feixue

College of Light Industry, Liaoning University, Shenyang 110036, China

As for the problem of congestion control in Internet, based on sliding mode control theory and Takagi-Sugeno（T-S）fuzzy model, a fuzzy sliding mode congestion control scheme is put forward. Considering uncertainty and time-varying delay factors in Internet, a network model is obtained by T-S fuzzy model for network system. An asymptotically stable sliding surface is designed by Linear Matrix Inequality（LMI）. It can effectively compensate for the effect of uncertainty and time-varying delay factors. The controller is designed by the way of reaching law, which can effectively constrain oscillation of the queue length in router. Simulation contrasts in many scenarios demonstrate that the proposed control scheme possesses better stability and robustness.

Internet congestion control; sliding mode control; T-S fuzzy model; active queue management

YAN Ming, FENG Chunyang, GAO Feixue. Fuzzy sliding mode congestion control scheme in Internet. Computer Engineering and Applications, 2014, 50（17）：100-105.

A

TP393

10.3778/j.issn.1002-8331.1210-0224

辽宁省自然科学基金（No.201202092）。

闫明（1974—），男，博士，副教授，研究方向为网络拥塞控制、滑模变结构控制等；冯春杨（1965—），女，讲师，研究方向为滑模变结构控制；高飞雪（1988—），女，硕士生，研究方向为网络拥塞控制。E-mail：yanm0219@163.com

2012-10-22

2012-12-11

1002-8331（2014）17-0100-06

CNKI网络优先出版：2013-01-11,http://www.cnki.net/kcm s/detail/11.2127.TP.20130111.0953.011.htm l