一类恒化器竞争模型正解存在区域的刻画

刘继远，李艳玲

陕西师范大学数学与信息科学学院，西安 710062

一类恒化器竞争模型正解存在区域的刻画

刘继远，李艳玲

陕西师范大学数学与信息科学学院，西安 710062

刻画了一类带Ivlev型反应函数的非均匀恒化器竞争模型正解的存在域。利用不动点指数理论和上下解方法证明了在a≠且b≠的前提下，系统有正解的充要条件是a＞r1(a，b)且b＞r2(a，b)。结合单调方法和不动点指数理论，说明存在域Λ是中的一个无界连通区域，其边界由两条递增的曲线Γ1:a=F1(b)和Γ2:b=F2(a)构成。证明了系统在存在域Λ的某个子区域内至少有两个正解。

恒化器；Ivlev型反应函数；不动点指数；单调方法

1 引言

恒化器模型是微生物学研究中一个很重要的模型。在恒化器中，微生物的增长与养料浓度之间有着密切的关系，这种关系可以用不同的反应函数来表示。由文献[1]知，微生物的增长与养料浓度之间的关系可以由Holling II型反应函数、Holling III型反应函数和Ivlev型功能反应函数来表示。另外，还可以由Beddington-DeAngelis型功能反应函数来表示，如文献[2]。目前，对于非均匀恒化器竞争模型的研究，讨论的多是Holling II型反应函数，如文献[3-7]，对Ivlev型反应函数涉及较少。鉴于此，本文考虑如下带Ivlev型反应项的n维反应扩散系统：

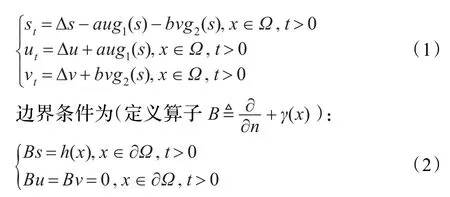
其中s，u，v分别表示营养液和两种竞争微生物的浓度；Ω是Rn(n≥1)中具有光滑边界的有界区域，gi(s)=1-e-ai(s)，ai＞0为常数，i=1，2；a＞0，b＞0是最大增长率；γ(x)，h(x)∈C(∂Ω)且γ(x)，h(x)≥0，≢0，x∈∂Ω;Γ0≜{x∈∂Ω:γ(x)=0}，Γ0≠Ø且Γ0≠∂Ω，h(x)＞0，x∈Γ0。

对于含有两种微生物的非均匀恒化器竞争模型的研究，已有不少相关文献，如文献[4，6-7]。文献[4]通过讨论一类具有M onond-M型反应项的一维恒化器模型，得到了相应平衡态系统的局部分歧。文献[7]研究了具有同样反应函数的n维恒化器模型，获得了共存解的全局分歧。文献[6]通过研究具有同样反应函数且带有一个内抑制剂的一维恒化器模型，确定了模型正解存在时两物种最大增长率的存在区域。本文的主要目的则是刻画系统（1）～（2）正解的存在区域。为此，首先考虑与式（1）～（2）相对应的平衡态系统：

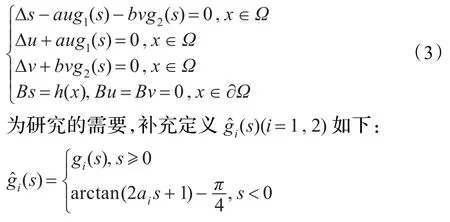
令z=s+u+v，则类似文献[7]的讨论知，z所满足的方程存在惟一解且为正解，不妨仍记为z。这样式（3）的任一非负解(s，u，v)满足s+u+v=z，x∈。把s= z-u-v代入式（3），得到本文将重点研究的边界值问题：

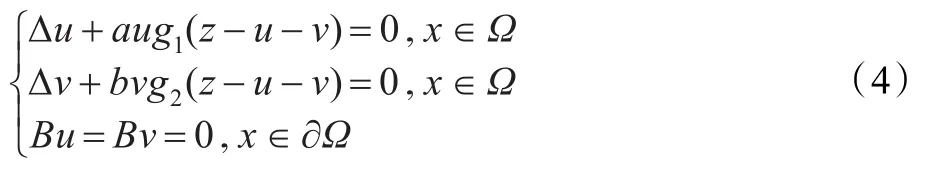
2 准备

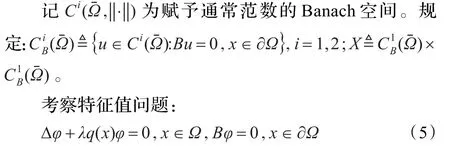
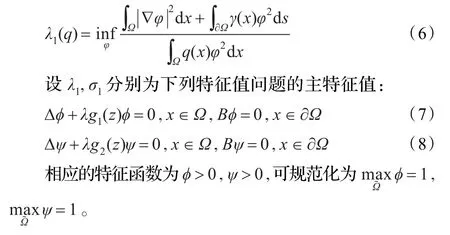
定义θλ1=0，由引理2.3，2.4和2.5知，θa关于a在[λ1，+∞)上连续且在上随着a的增加而逐点增加。

注1在式（4）中令(u，v)=(0，v)，可得另一单物种方程：

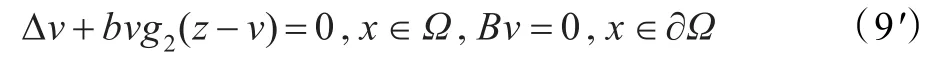
易知，关于式（9'）有如下类似式（9）的结论：

（1）当b＞σ1时，式（9'）有唯一正解，记为νb；b≤σ1时，式（9'）只有零非负解。

（2）定义νσ1=0，则νb关于b在[σ1，+∞)上连续且在上随着b的增加而逐点增加。

（3）定义式（9'）在νb处的线性化算子为Lb=Δ+ b(g2(z-νb)-νbg′2(z-νb))，则λ(Lb)＜0。

3 正解的存在性

记gi(u，v)=gi(z-u-v)，i=1，2，则gi(u，v)关于u，v递减，此时方程（4）变为：

4 存在域Λ的特征及正解的多重性

5 小结

设(u，v)是式（4'）的正解，则由g1(u，v)＜g1(0，0)，g2(u，v)＜g2(0，0)知，a＞λ1，b＞σ1。这说明a＞λ1，b＞σ1是式（4'）有正解的必要条件。本文即是在的子区域R0=(λ1，+∞)×(σ1，+∞)内讨论参数(a，b)的取值变化对式（4'）正解的影响，进而找到式（4'）有正解时参数(a，b)的准确存在区域。在第3章，通过将参数(a，b)限制在两条递增的曲线a=和b=a)所围的区域内，保证了式（4'）正解的存在性，这给出了式（4'）有正解的充分条件（定理3.1）。但由于对(a，b)的限制太严，漏掉了(a，b)可取的其他很多值。因而在第4章，设法利用定理4.1来弥补这个缺陷：通过给出式（4'）在a≠b≠(a)的前提下有解的充要条件，放宽存在域的可能范围。最终，通过定理4.2说明式（4'）有正解时(a，b)的准确存在域是R0上的一个无界连通区域，且以两条递增曲线a=F1(b)和b=F2(a)为其边界。至此，可知{(a，b): a＞F1(b)，b＞F2(a)}=Λ=R1∪R2∪R3∪R4，其中R1={(a，b):

ffff5d(b)，b＞ffff5c(a)}。而且，当(a，b)取自R2∪R4时，式（4'）至少有两个正解（定理4.3）。

[1]阮世贵.恒化器模型的动力学[J].华中师范大学学报：自然科学版，1997，31（4）：377-397.

[2]李艳玲，李海侠，吴建华.一类非均匀Chemostat模型的共存态[J].数学学报：中文版，2009，52（1）：141-152.

[3]Hsu S B，Waltman P.On a system of reaction-diffusion equations arising from competition in the unmixed chemostat[J].Society for Industrial and Applied Mathematics，1993，53：1026-1044.

[4]So W H，Waltman P.A nonlinear boundary value problem arising from competition in the chemostat[J].Applied Mathematics and Computation，1989，32：169-183.

[5]Nie H，Wu J.Asymptotic behavior on a competition model arising from an unstirred chemostat[J].Acta Mathematicae Applicatae Sinica，2006，22（2）：257-264.

[6]Nie H，Zhang H，Wu J.Characterization of positive solutions of the unstirred chemostat with an inhibitor[J].Nonlinear Analysis：Real World Applications，2008，9（3）：1078-1089.

[7]Wu J.Global bifurcation of coexistence state for the competition model in the chemostat[J].Nonlinear Analysis，2000，39：817-835.

[8]Figueiredo D G，Gossez J P.Strict monotonicity of eigenvalues and unique continuation[J].Communications in Patial Differential Equations，1992，17：339-346.

[9]Keener J.Principles of applied Mathematics[M].Massachusetts：Addison-Wesley，1987.

[10]Smoller J.Shock waves and reaction-diffusion equations[M].New York：Springer，1984.

[11]Protter M H，Weinberger H F.Maximum principles in differential equations[M].New York：Spring-Verlag，1984.

[12]Dancer E N.On positive solutions of some pairs of differential equations[J].Jrans Amer Math Soc，1984，284（2）：729-743.

[13]王明新.非线性椭圆型方程[M].北京：科学出版社，2010.

[14]Amann H.Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces[J].SIAM Review，1976，18（4）：620-729.

[15]叶其孝，李正元.反映扩散方程引论[M].北京：科学出版社，2011.

LIU Jiyuan, LI Yanling

College of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710062, China

The existence region of positive solutions in the unmixed chemostat with the Ivlev response function is portrayed.It is shown that if a≠and b≠hold,then the necessary and sufficient conditions,where the system possesses positive solutions,are a＞r1(a，b)and b＞r2(a，b)by using the fixed point theory and the upper and lower solution method. Combining with the monotone method and the fixed point theory,it is proved thatis a connected unbounded region in,whose boundary consists of two monotone nondecreasing curvesΓ1:a=F1(b)andΓ2:b=F2(a).It is shown that the system has at least two positive solutions in certain subregion of.

chemostat; Ivlev response function; fixed point index; monotone method

LIU Jiyuan, LI Yanling. Characterization of existence region of positive solutions for competition model in chemostat.Computer Engineering and Applications, 2014, 50（17）：68-73.

A

O175.26

10.3778/j.issn.1002-8331.1209-0023

国家自然科学基金（No.10971124）；教育部博士点专项基金（No.200807180004）。

刘继远（1984—），男，硕士研究生，研究领域为偏微分方程理论及应用；李艳玲（1963—），女，通讯作者，博士，教授，研究方向为反应扩散方程及其应用。E-mail：yanlingl@snnu.edu.cn

2012-09-10

2012-11-28

1002-8331（2014）17-0068-06

CNKI网络优先出版：2012-12-26,http://www.cnki.net/kcms/detail/11.2127.TP.20121226.1120.003.htm l