基于随机模型的云平台资源调度策略设计

赵少卡，李立耀，徐聪，杨家海

1.福建师范大学福清分校数学与计算机科学系，福建福清 350300

2.清华大学网络科学与网络空间研究院，北京 100084

基于随机模型的云平台资源调度策略设计

赵少卡1，2，李立耀1，徐聪2，杨家海2

1.福建师范大学福清分校数学与计算机科学系，福建福清 350300

2.清华大学网络科学与网络空间研究院，北京 100084

针对云计算资源管理的实际需求，提出一种基于随机模型的云平台调度策略，设计合理高效的资源调度算法，解决传统代数模型请求丢失率高以及其他随机模型负载均衡指标性能较差的问题，从而在服务性能和执行效率的基础上保证服务器的资源负载，使云平台处于相对稳定的状态。在实验环境中的验证结果表明，该调度策略能够优化虚拟资源的使用效率和服务响应时间，同时能够达到较好的负载均衡并降低运营成本。

云计算；资源调度；负载均衡；随机模型

1 引言

伴随着分布式计算特别是网格技术的发展，产生了云计算这一新型的服务计算模型。云计算体系架构中，基础设施即服务（Infrastructure as a Service，IaaS）以服务的方式为用户提供包括处理、存储、网络和其他基本的计算资源的使用，用户可以在其申请到的虚拟资源中部署或运行应用程序，而不需要了解计算资源提供过程的细节。随着数据中心规模的日益增大，云平台中服务器的数目不断增加，同时虚拟化环境也日趋复杂，这种情形下如果不能够提升IaaS平面的管理能力，使其能够充分全面地调度数据中心的各项资源，则很大程度上会降低整个数据中心的工作性能。因此，虚拟资源的调度问题成为IaaS平台中的一个主要问题，设计并实现一套较为完善的资源调度策略具有十分重要的理论和现实意义。

2 云平台调度的研究现状

资源调度是将资源从提供方分配给用户的过程。云数据中心的资源调度技术是云计算应用的核心，是云计算得以大规模应用和提高系统性能、兼顾节能减排的关键技术。现有的IaaS调度策略主要分为两种，一种是基于代数模型[1-4]，主要是以最优化服务性能为目标的M in-m in调度策略、suffrage调度策略，以优化系统性能指标为目标的Best-Fit、First-Fit调度策略，以及其他一些以优化经济收益为目标的调度策略。这些调度策略主要以提高云计算系统的总体吞吐率为核心的优化目标，如最优化请求的响应时间、请求处理效率等服务质量指标，以及服务器负载状况、资源利用率等系统性能指标。总体来看，目前大部分云计算平台使用的都是基于代数模型的调度策略，这些策略虽然能够满足当前的调度达到最优值，但是缺乏对于阶段性调度结果的总体评估，并经常导致请求的丢失以及系统整体吞吐率的下降。

另一种是基于随机模型的调度机制[5-7]，希望在保证系统及服务性能的同时降低请求的丢失率，但目前的随机调度机制虽然弥补了代数模型的诸多不足，但针对云计算平台调度特点来说，依然存在缺陷，例如，在优化系统及服务性能指标时忽略了服务器负载均衡方面的指标。因此，一种基于随机模型更为完善的调度机制亟待提出。

3 模型设计

本算法模型基于随机模型的云平台资源负载均衡调度策略，主要分为两部分：服务请求的队列排序和服务器优化选择。用户发送申请虚拟机请求到达云队列，队列将根据用户请求的优先级进行排序，将第一个请求发送至服务器进行分配，云端根据负载均衡算法，挑选出最合适的服务器接受这一待处理的请求（如图1所示）。其中，第一部分主要是对资源请求的调度，在优化服务指标性能的Best-Fit算法思想基础上引入随机模型，使用基于优先级别的队列，减少轻量级服务请求被丢弃的概率以及请求积压的数量，提高系统的吞吐率；第二部分是对目标主机的选择，在综合考虑服务器负载情况以及资源请求的积压状况的情况下，选择相应时间最快同时负载情况相对较小的目标主机进行虚拟资源的分配，使得调度策略在优化服务性能指标的同时，在服务器负载均衡方面效果更佳。

3.1 模型的评价指标

（1）服务请求丢失率(R0(t))

在一时间单元t内有NA(t)个服务请求到达，其中如果有N0(t)个请求由于队列溢出而被丢弃，则定义该时间单元内服务请求的丢失率为：

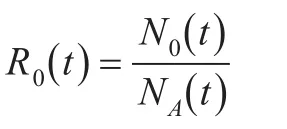
（2）服务请求积压状况(L(t))

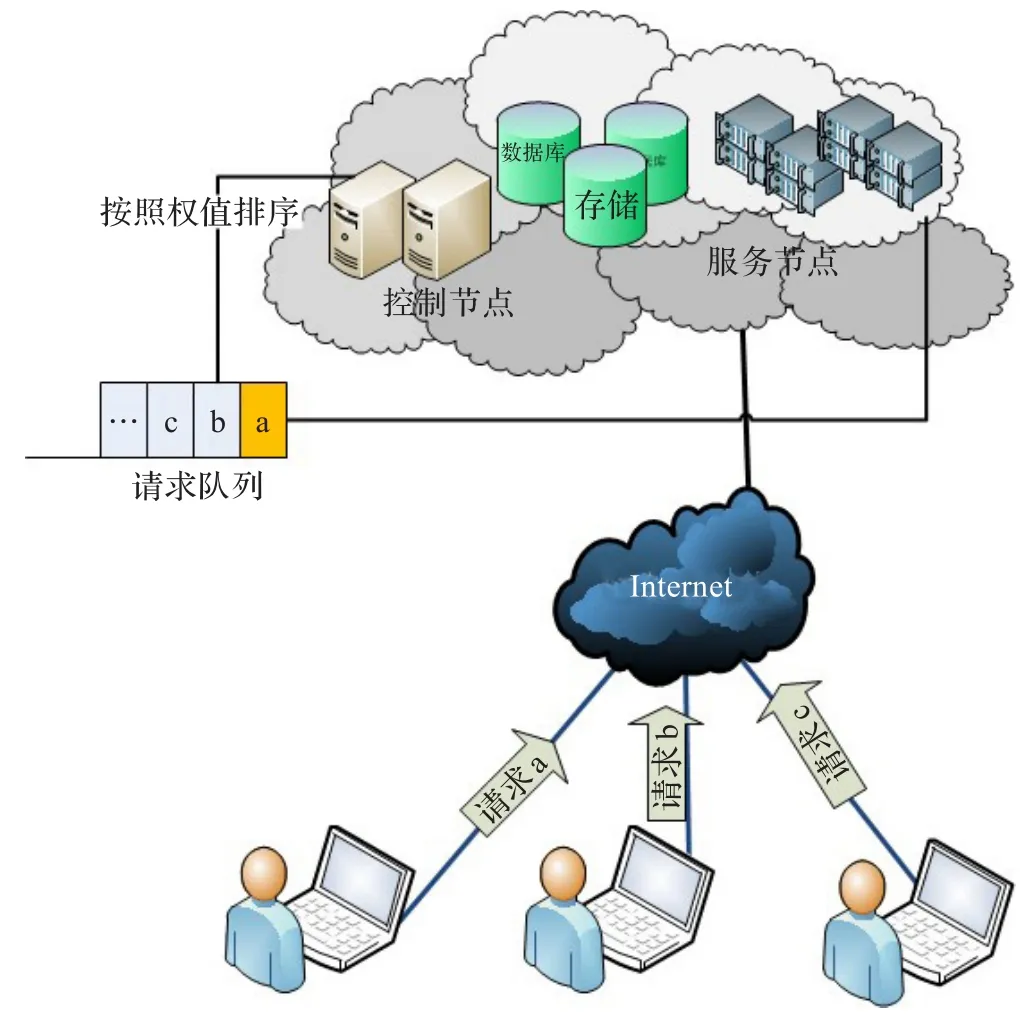
图1 算法模型示意图

服务请求的积压状况记录了在某一时刻尚未被处理的请求的数目，请求积压情况越严重，则该时刻服务响应的效率就会下降。具体地，定义t时刻某项服务m被积压的请求数目为Lm(t)，该时刻的请求积压量由前一时刻的请求积压量，t时刻内到达的新的请求数目Am(t)以及t时刻内处理掉的请求的数目Hm(t)共同决定，具体关系为：

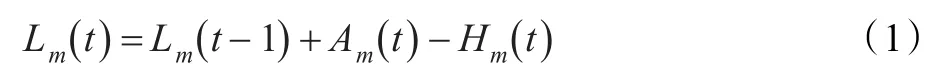
对于云系统整体的资源调度队列，t时刻所有任务积压量的总和L(t)则表示为：

为了减小请求的丢失情况同时提高系统的响应时间，增大吞吐率，合理的调度策略应当使系统处于稳定状态时，请求积压量维持在一个有限值，即尽可能地满足：

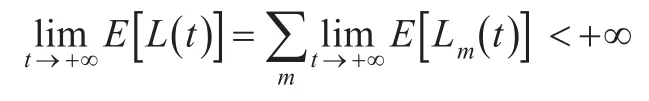
（3）平均请求处理时间(tm)

服务的平均请求处理时间反映了云计算系统处于稳定状态时平均的工作效率。平均请求处理时间的长短不仅与稳态时系统的请求积压量有关，而且与请求到达的速率相关。具体来说，假设某项IaaS服务m的请求到达服从强度为λm的泊松分布，那么云平台达到稳定状态时，该服务请求的平均处理时间tm为：

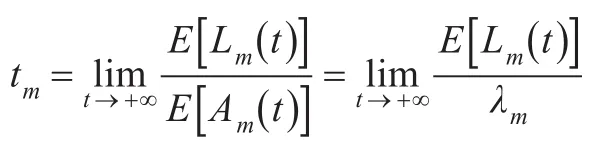
（4）云服务器负载均衡状况(σDC)

在某一时刻t时，设一个由N台服务器组成的云计算IaaS平台中，第i台服务器的资源利用率为P(t)，那么在这一时刻整个IaaS平台的平均负载状况AvgDC可以被定义为：

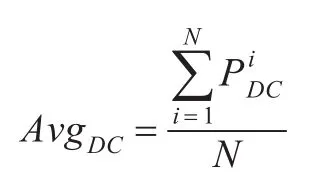
同时，用σDC来定义云服务器的负载均衡状况，σDC的值越小则服务器的负载越均衡：

在具体的IaaS资源调度场景中，初始开始调度时服务请求的积累量相对较小，服务丢失率较低，平均响应时间也很快。随着不同种类服务调用请求的增加，有限的IaaS资源不能同时满足所有的请求需求，会导致请求的不断积压，L(t)的值不断增大，同时请求的平均处理时间tm逐渐增加；当某一时刻，积压的请求量大于系统设定的等待队列的上限时会造成服务请求的丢失，出现R0＞0的情况；最终，随着调度过程的不断继续，云计算系统最终会处于一个相对稳定的状况，系统的各项性能评价指标会相对稳定在一个固定的值上，本调度策略主要对系统处于稳态时各项性能指标进行综合的优化与分析。

在云计算IaaS平台处于稳定状态时，如果R0＞0，但服务积压量L(t)的值很小，说明该调度策略将很多对虚拟资源需求量较大的重量级任务积压在了队列当中，虽然响应时间能够保证相对较小，但吞吐率并不大，不是理想的调度策略，需要改变每次优先选取的任务，增大资源的分配粒度；如果服务积压量L(t)的值一直处于最大值，则任务一直处于大量积压状态，这种情况会造成任务请求的大量丢失，也不是理想的调度策略，需要对被积压的服务特征进行分析，采用优先排队的策略，减小等待队列的长度；如果服务积压量L(t)、服务丢失率R0以及响应时间tm的值都比较理想，但是负载均衡参数σDC的值较大，说明该方法对于任务的排序方式是合理的，但服务器的选择方面不能保证负载均衡的情况，需要优化服务器选择的方式。

3.2 模型的详细设计

3.2.1 服务请求的队列排序

模型的第一步就是要进行服务请求的队列排序，目的是在保证吞吐率的前提下，使等待队列的长度维持在一个固定的上限之内，避免出现无限等待的情况。和其他的调度方式类似，本调度策略中也使用等待队列对暂时无法处理的服务请求进行排队，当其他任务释放之后，云平台具备了足够的资源，会从队列之中选择合适的任务进行处理。目前通用的调度算法之所以阶段性调度结果并不理想，是因为大部分的调度策略都是单目标优化的代数过程，一方面这些策略仅考虑了瞬时调度的最优情况而忽略了阶段性整体调度的情况，导致了大量请求的积压以及无限等待的情况出现；另一方面，这些策略的优化目标一直是固定的，而实际调度过程的不同阶段往往需要根据实际需求不断调整调度策略的优化目标，如当平台资源剩余较多时应以最大化吞吐率为优化目标，尽量多地将剩余资源分配出去，而当请求积压严重时，应以最大限度减小积压状况，提高服务响应时间为优化目标，此时往往需要调度一些轻量级的服务，目前的调度算法由于忽略了这些因素导致结果调度并不理想。本调度算法将根据调度过程的不同阶段不断调整优化目标，使整体的阶段性调度结果达到一个相对理想的状态。

首先，在云计算平台资源富裕的情况下，调度策略以优化每次调度的吞吐率为首要目标，此时的调度策略与Best-Fit算法相似，每次选取资源需求最大的请求进行处理。假设t时刻服务m（比如某种特定种类的虚拟机模板）对某种硬件资源k（如：CPU、内存等）的需求量为Dmk，服务器i对该资源的占有总量为Cik，同时该时刻服务器中已经分配了Nmi(t)个服务m资源，则三者应当满足的约束条件为（M为总的服务种类数目）：

此时的调度策略可以抽象成为如下的优化模型，此时由于请求积压量较小，不足以影响调度的效率，因此，单次调度的资源数目作为首要的优化目标，而服务器的资源总量作为主要的限制条件。

其中，K为硬件资源的总的种类数目，M(t)为t时刻已被触发的服务种类的集合，MaxqueueLength为等待队列的队长上界。此时以优化一次调度的资源总量为目标，调整等待队列中服务请求的顺序，将资源需求量最大的服务置于队首优先被处理。

随着调度的进行，资源的需求量逐渐达到或超过云系统的资源总量，此时沿用先前的调度策略会造成大量的请求被积压，此时应以尽量增加调度任务的数目，减小任务的积压，减少服务请求的丢失率为首要调度目标，优化模型调整为：

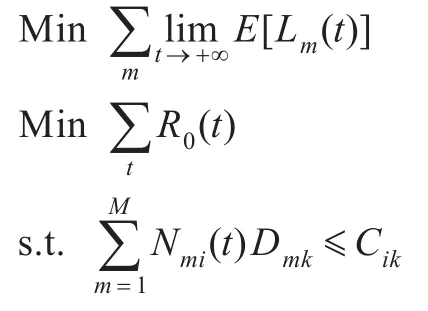
此时的调度以尽量减少任务积压为目标，在云平台资源紧张的情况下，可以考虑适当增加轻量级任务的优先级，减少等待队列的长度。此时的优先队列会增加轻量级任务在队列中的优先级，由于在上一个场景中，轻量级任务往往会在队列中积压，因此本策略除了任务对资源的需求量之外还根据任务的积压时间来调整不同服务请求的优先级。

之后，云计算系统进入了稳定状态，队列中任务的积压量，系统的平均吞吐率和任务处理的响应时间会维持在一个相对稳定的范围之内。在稳定状态时，由于云计算系统仍然处于资源供不应求的阶段，因此，一个比较理想的调度策略应当尽量减小任务的积压量，即使得等待队列尽量不要出现溢出的情况：

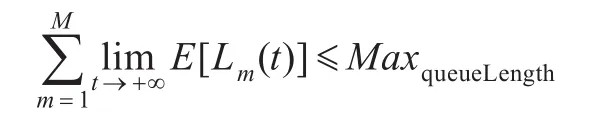
本文提出的资源调度策略，在服务请求排序的部分以稳态时任务的积压状况为主要的优化目标，在保证等待队列不会溢出的前提下，尽量优化每次资源分配的吞吐率，使得该排队策略能够根据调度过程的各个阶段不断调整调度的优化目标，从而使阶段性的调度结果尽可能达到最优。

3.2.2 服务器的选择

第一部分对服务请求的优先排序主要是合理调整资源调度任务执行的先后顺序，优化服务积压量、服务请求响应时间等服务质量指标；而第二部分的工作主要是对每个服务请求，在最合适的服务器上进行资源的分配。与第一部分考虑的服务质量因素不同，该部分主要考虑的因素是云计算系统服务器的负载均衡问题。

该部分调度模型引入一些新的参数：

pni(t)：t时刻服务n请求的资源被分配到服务器i上的概率。

Dnk：t时刻位于队首的服务n请求的资源k的数量。此时，t时刻服务器i的资源负载可以表示为：

云计算平台的平均负载状况AvgDC则可表示为：

此时在考虑服务器负载情况的同时，也考虑了每个服务器的任务积压情况，在尽量满足负载均衡的前提下，减少每个服务器中的任务积压量。设t时刻服务器i的任务积压量为qi(t)，t时刻处理结束的任务数目为hi(t)，则有：

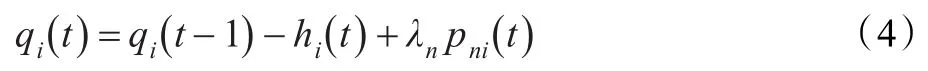
将上述影响因素综合考虑，第二部分的调度策略可以抽象为一个多目标的优化模型，具体形式化描述如下：

服务器选择策略的优化过程，就是不断调整pni(t)取值的过程，使得σDC(t)和qi(t)的取值都达到相对理想的情况。具体算法实现过程中，选择负载相对较轻的一些服务器作为候选服务器集合，之后比较该集合中所有服务器的任务积压量，综合考虑负载均衡与服务效率两方面的因素，选择积压量较小的服务器进行资源的分配。

3.3 模型的算法步骤

3.3.1 服务请求的优先排队

对于每个提交给云计算系统的服务调用请求，执行以下步骤：

步骤1根据具体的系统规模、服务数量以及调度执行的阶段，初始化如下参数：

Dmk：服务m所需要的虚拟资源k的数量，此参数在算法执行开始时初始化。

Mapn：任务n对应的服务种类，此参数在第n个任务到达队列时初始化。

Tn：任务n的积压时间，此参数在第n个任务到达队列时初始化，初始值设为1。

Wn：等待队列中任务n的权重，此参数在第n个任务到达队列时初始化，初始值设为Mapn。

MaxqueueLength：等待队列的队长上限值，此参数在算法执行开始时初始化。

Fexecute：每次调度执行的频率（以分钟、小时为时间单元来执行调度），此参数在算法执行开始时初始化。

R0(t)：t时刻服务请求的丢失率，此参数在算法执行开始时初始化，初始设为0。

L(t)：t时刻等待队列中任务的积压量，即队列长度。此参数在算法执行开始时初始化，初始值设为0。

步骤2初始化时间计数器t=1，随着调度过程的推进，每经过一个时间单元，计数器增加t=t+1，在每个时间单位Fexecute中依次执行以下步骤：

步骤2.1将任务计数器count变量设为0，该时间单位每到达一个新的服务请求，count变量值加1。

步骤2.2判断此时L(t-1)+count与MaxqueueLength的大小关系，若二者大小关系满足L(t-1)+count≤MaxqueueLength，则将所有请求排入队列当中；若不满足此关系则丢弃掉多余的请求，更新R0(t)的值。

步骤2.3对于等待队列中的每一个任务n，依次执行以下步骤：

（1）重新计算该任务在以资源k为核心的调度过程中所占的权重。

Wn=DMapnkTn

（2）根据新的权重值重新调整该任务在队列中的位置，权重越大的任务在队列中的位置越靠近队首。

（3）所有任务的队列位置调整完毕之后，结束步骤2.3。

步骤2.4如果经过步骤2.3后，对于处于队首的任务，根据服务器选择策略的结果（在3.3.2节中进行详细描述），在适当的服务器中进行资源的分配。

步骤2.5根据式（1）、式（2）更新L(t)的值。

步骤2.6对每个仍然处在等待队列中的任务i，更新任务积压时间Ti=Ti+1。

步骤3一段时间之后，如果等待队列一直处于满载状况，同时请求丢失概率一直处于接近100%，说明此时的队长上限不适合请求到达的速率，需要增加队长上限MaxqueueLength的取值，之后返回步骤1重新观察系统性能能否达到稳定状态。如果等待队列的长度处于一个相对稳定的取值范围内，同时请求丢失率维持在一个相对较低的程度，说明系统在此排队策略下达到了稳态，返回步骤2，请求排队可以继续按该策略进行。

3.3.2 服务器的优化选择策略

对于每个处于等待队列队首，即将要被处理的请求，执行以下步骤：

步骤1根据具体的系统规模、服务数量以及调度执行的阶段，初始化如下参数：

qi(t)：t时刻服务器i的等待队列中任务的积压量，即队列长度。此参数在算法执行开始时初始化，初始值设为0。

Cik：服务器i对资源k的占有总量，此参数在算法执行开始时初始化。

Nmi(t)：t时刻服务器i上已经分配了的服务m的数目。此参数在算法执行开始时初始化，初始值设为0。

isHandled：布尔变量，记录当前资源分配任务能否被处理，1表示可以，0表示无法处理。参数在算法执行开始时初始化，初始值设为0。

candidateSet：数组，记录针对每个任务可能的候选服务器的集合，参数在每次请求处理进程被触发时（即步骤2执行时）都进行一次初始化，初始值为空。

N：云计算平台服务器的总数，参数在算法执行开始时初始化。

β：调整阈值，用来限定每次优化选择的可行区间的规模，参数在算法执行开始时初始化，在本方法中初始值设为30%。

步骤2当第一部分排队策略选出服务m的请求处理进程被触发时，对于每个服务器i，依次执行以下步骤：

步骤2.2计算并更新该服务器的剩余资源Cik(1-P(t))，并与服务需求的资源量Dmk作比较，若Cik(1-P(t))≥Dmk，则说明该服务器有能力处理该服务请求，将isHandled的值调整为1，并将该服务器加入到候选服务器集合中，更新集合candidateSet中的元素。

步骤3根据步骤2执行之后的结果，若isHandled的值为0，说明目前云平台的剩余资源量不足以处理该服务请求，本次任务调度终止，返回任务调度失败的结果，等待其他任务结束之后资源的释放；若isHandled的值为1，说明目前云平台的剩余资源量可以处理该服务请求，进入步骤4继续完成服务器选择的操作。

步骤4步骤3执行之后，判断候选服务器集合中元素的数目，并与服务器总数进行比较，若|candidateSet|≤Nβ，则说明可选服务器并不多，目前大部分服务器都处于负载较重的状况，此时直接进入步骤6，考虑优化服务响应时间；若|candidateSet|＞Nβ，则说明目前服务器负载情况不是很严重，此时以优化负载均衡状况为第一目标，进一步精简候选服务器集合的数目。

步骤5步骤4执行之后，根据candidateSet集合中每个服务器i的剩余资源量Cik(1-P(t))对candidateSet集合中的元素进行筛选，集合中只保留剩余资源量相对较大的前Nβ个服务器，更新candidateSet集合。

步骤6对于candidateSet集合中的每个服务器i，依次执行如下的操作：

步骤6.1计算该服务器的任务积压量qi(t)。

步骤6.2令Pmi(t)=1，Pmj(t)=0，i≠j，根据式（3）、（4）计算σDC(t)的值并记录。

步骤7选出使得σDC(t)达到最小值时的候选服务器j，在服务器j上根据服务m的需求分配虚拟资源，更新P(t)、Cjk、qj(t)的取值，返回并记录分配结果。步骤8时间单元t结束时，对云平台的每个服务器i，判断该服务器上是否有资源回收的操作被触发，如果有，则根据回收的资源量依次更新P(t)、Cjk、qj(t)的取值。

步骤9返回步骤2，进行下一次的服务器选择。

基于随机模型的云平台资源负载均衡调度策略的具体算法流程如图2所示。

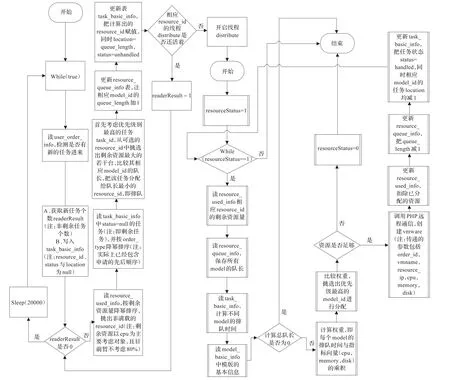
图2 基于随机模型的负载均衡调度算法流程

4 实验与分析

4.1 实验环境

基于开源软件OpenStack搭建一个包含6台服务器的云计算IaaS平台，服务器详细配置如表1所示。该平台以虚拟资源的方式为用户提供虚拟资源的使用，提供的虚拟资源的模板种类如表2所示。为了对本文调度策略进行评估，将本文提出的调度算法用Java语言进行实现，并和目前使用较为广泛使用的诸多调度策略进行了对比实验。

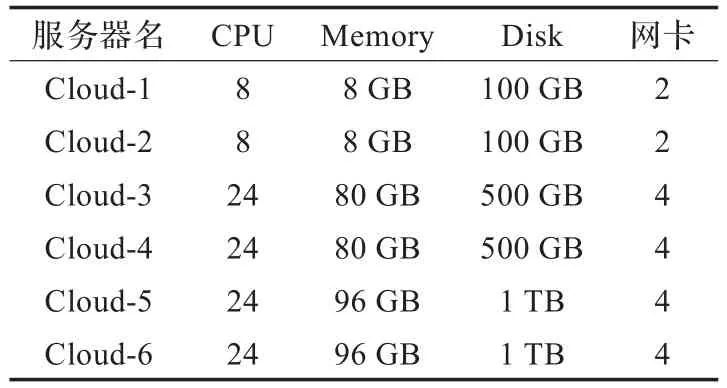
表1 云计算IaaS平台服务器配置

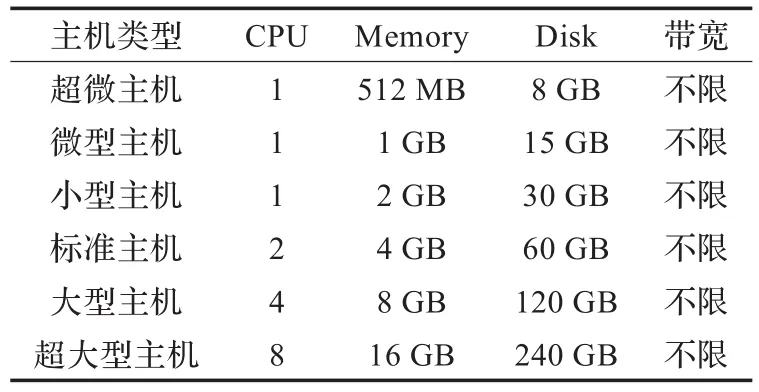
表2 云平台虚拟资源模板

具体实验中，将表2中列出的服务类型按照占用资源由小到大进行排序，编号为服务1～服务6，对应每种服务模拟出一串服从特定强度的泊松到达请求序列。根据实际需求量的统计，用户对微型、小型主机的需求比对大型、超大型主机的需求量明显要大，因此在本实验中服务1～服务6的请求到达频率依次递减。采用不同的调度策略用于对服务请求进行调度并对虚拟资源进行分配，本实验重点考察的调度策略有目前使用较为广泛的Best-Fit、M in-m in调度策略，OpenStack开源软件提供的SimpleSchedule、ChanceSchedule分配策略，学术界提出的随机调度策略以及本文提出的调度策略等。

实验通过在500个时间单位内，统计不同调度算法的任务积压量和机器平均负载均衡状况进行对比。任务积压量从第一个时间片就开始采集，负载均衡是在各节点达到稳态时进行数据采集。由多次实验数据得到，从第300时间单位开始，各节点的CPU负载情况基本处于稳态，因此负载均衡的实现结果选择从第300个时间点开始统计，每隔5个时间点采集一次数据，到500个时间单位结束后，计算每个节点的平均负载情况。

4.2 实验结果与分析

实验结果显示，本文提出的调度算法不论在任务积压量还是服务器的负载均衡指标上都有明显较优的结果。

图3显示了随着调度过程的进行，使用不同的调度方法时造成的任务积压的状况。从中可以看出，本调度策略在任务积压量指标上明显优于Best-Fit和M in-M in策略，与其他随机调度策略相比基本持平。使用以优化单次调度吞吐量和单次调度响应时间为目标的Best-Fit和M in-m in策略处理请求时，调度初始阶段效果相对较为理想，但随着越来越多的资源被分配出去时，由于这两个策略缺乏对调度效果的阶段性评估，导致大量单次未被调度的请求被积压。而使用基于随机模型的优先队列排序，考虑到了阶段性调度的总体性能，提高了被积压任务的优先级，在云平台负载较轻的阶段保证任务调度吞吐率的同时，在负载较重时能够减小任务的积压量，避免积压量无限增长的情况出现。

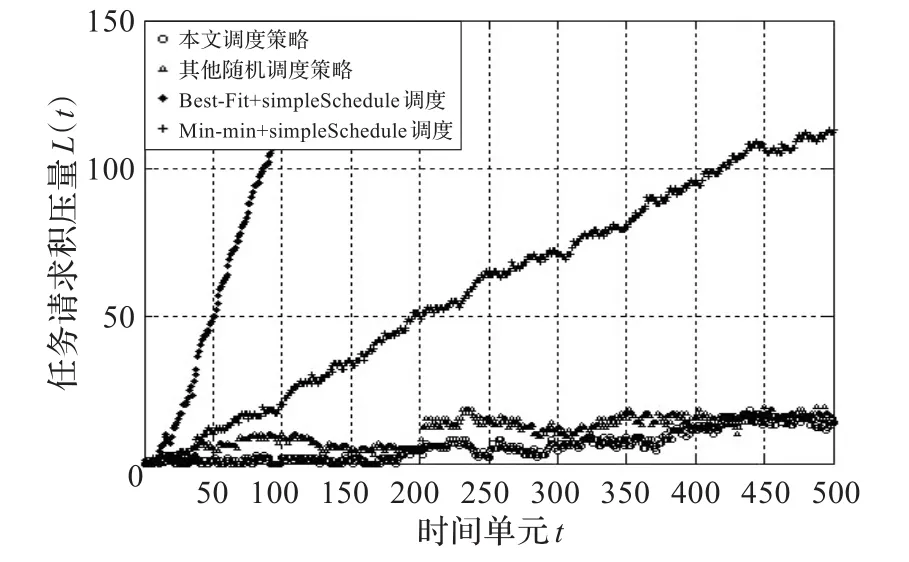
图3 各算法在任务积压量上的结果

图4显示了本调度策略在负载均衡指标上明显优于各类对比算法。由于同时考虑了任务积压情况qi(t)和资源负载情况P(t)，使得本方法在负载均衡方面相比其他调度方法也有明显的优势。其他的基于随机模型的调度策略，虽然在请求调度上也做到了减小任务的积压和请求的丢失，但在服务器选择部分考虑的因素不够全面，导致服务器负载均衡的效果并不理想。

图4 各算法在负载均衡上的结果

通过和其他算法调度结果的对比分析，本调度策略使用了基于随机模型的优先队列，在云平台负载较轻时优化了资源调度算法的吞吐率，在云平台资源负载较重时减小了任务的积压量和请求的丢失率；同时本策略在服务器选择策略上综合考虑了服务器的资源负载情况以及任务积累情况，在保证服务性能和执行效率的基础上尽量均衡了服务器的资源负载，使云平台处于相对稳定的状态。由于解决了现有调度策略存在的一些问题，调度结果在某些服务质量指标的衡量下效果更加理想。因此，本文提出的调度算法是一个满足云平台资源调度要求的良好的策略。

5 结束语

本文设计并提出一种基于随机模型考虑负载均衡的调度策略，解决基于代数模型的调度策略请求丢失率高以及其他基于随机模型调度策略负载均衡指标性能较差的问题，以优化云计算IaaS平台的整体性能。通过与Best-fit，M in-m in等经典算法和其他随机模型调度实验比较发现，该算法在较少任务积压量和负载均衡上都具有良好的性能。在下一阶段，云计算服务调度策略的运行环境的复杂性将进一步增强，扩充云系统的集群数量和部署更丰富的异构环境加以测试与验证，并不断完善调度策略。

[1]Speitkamp B，Bichler M.A mathematical programming approach for server consolidation problems in virtualized data centers[J].IEEE Transactions on Services Computing，2010，3（4）：266-278.

[2]Beloglazov A，Buyya R.Energy efficient allocation of virtual machines in cloud data centers[C]//10th IEEE/ACM International Conference on Cluster，Cloud and Grid Computing，2010：577-578.

[3]Qin X，Xie T.An availability-aware task scheduling strategy for heterogeneous systems[J].IEEE Transactions on Computers，2008，57（2）：188-199.

[4]Song S，Hwang K，Kwok Y.Risk-resilient heuristics and genetic algorithms for security-assured grid job scheduling[J].IEEE Transactions on Computers，2006，55（6）：703-719.

[5]Maguluri S T，Srikant R，Ying L.Stochastic models of load balancing and scheduling in cloud computing clusters[C]//Proceedings of IEEE INFOCOM Conference，2012.

[6]Bramson M，Lu Y，Prabhakar B.Random ized load balancing with general service time distributions[C]//Proceedings of the ACM SIGMETRICS International Conference on M easurement and modeling of Computer Systems，New York，USA，2010：275-286.

[7]Maguluri S T，Srikant R，Ying L.Heavy traffic optimal resource allocation algorithms for cloud com puting clusters[C]//International Teletraffic Congress，2012.

[8]林伟伟，齐德昱.云计算资源调度研究综述[J].计算机科学，2012，39（10）：1-6.

[9]田文洪.云计算资源调度管理[M].北京:国防工业出版社，2011.

[10]左利云，曹志波.云计算中调度问题研究综述[J].计算机应用研究，2012，29（11）：4023-4027.

ZHAO Shaoka1，2,LI Liyao1,XU Cong2,YANG Jiahai2

1.Department of Mathematics and Computer Science, Fuqing Branch of Fujian Normal University, Fuqing, Fujian 350300, China
2.Institute for Network Sciences and Cyberspace, Tsinghua University, Beijing 100084, China

In view of cloud computing actual needs of resource management, cloud platform scheduling strategy based on stochastic model is proposed, and reasonable and efficient resource scheduling algorithm is designed in order to reduce the request loss rate of traditional algebraic model and improve poor load balancing performance of other stochastic models.Through load balancing on the basis of service performance and efficiency, cloud platform stability is ensured. Experimental results show that the scheduling strategy can optimize the efficiency of virtual resource usage and the response time of the service while being able to achieve better load balance and reduce operating costs.

cloud computing; resource scheduling; load balancing; stochastic model

ZHAO Shaoka, LI Liyao, XU Cong, et al. Cloud platform resource scheduling strategy design based on stochastic model. Computer Engineering and Applications, 2014, 50（17）：56-62.

A

TP393

10.3778/j.issn.1002-8331.1306-0101

教育部-中国移动研究基金（No.MCM 20123041）；福建省教育厅科技项目（No.JB13198，No.JA 13343，No.JA 12352）；福建师范大学福清分校科技研究项目（No.KY 2013001）。

赵少卡（1980—），男，讲师，主要研究领域为云计算、软件工程；李立耀（1970—），男，副教授，主要研究领域为计算机网络；徐聪（1986—），男，博士研究生，主要研究领域为计算机网络；杨家海（1966—），男，博士，教授，主要研究领域为计算机网络。E-mail：zska@cernet.edu.cn

2013-06-13

2013-08-09

1002-8331（2014）17-0056-07

CNKI网络优先出版：2013-10-17,http://www.cnki.net/kcms/detail/11.2127.TP.20131017.1529.011.htm l